基于GM（1, 1）-Markov模型盐雾侵蚀对纤维混凝土耐久性能的影响

于剑桥, 乔宏霞, 2, *, 朱飞飞, 王新科

（1.兰州理工大学土木工程学院, 甘肃兰州 730050；2.兰州理工大学西部土木工程防灾减灾教育部工程研究中心, 甘肃兰州 730050）

盐雾侵蚀对混凝土材料来说是个长期过程, 判定混凝土能否在设计参考期内完成预定使用功能尤为重要.GM（1, 1）模型以“小样本、差信息”的不确定系统为研究对象, 为混凝土寿命预测提供了强有力的技术支持.然而, 传统GM（1, 1）模型考虑的因素过于单一, 预测精度有一定缺陷[7］.鉴于此, 本文以玄武岩-PVA纤维混凝土为研究对象, 进行了盐雾侵蚀加速试验, 根据耐久性试验数据及扫描电镜（SEM）观察到的侵蚀产物对混凝土损伤劣化规律进行分析, 并基于GM（1, 1）-Markov模型对混凝土寿命进行预测, 最终评估了纤维混凝土抗盐雾侵蚀的可靠性.

1 试验

1.1 原材料与配合比

甘肃祁连山水泥厂提供的P·O 42.5普通硅酸盐水泥, 安定性合格；比表面积为440 m2/kg的Ⅱ级粉煤灰；细骨料为细度模数2.73的天然河砂；粗骨料为表观密度2 780 kg/m3的碎石子；最大减水率（质量分数, 文中涉及的含量、水胶比等除特殊说明外均为质量分数或质量比）为20%的聚羧酸系高效减水剂；自来水；单丝分散玄武岩纤维（BF）, 长度为12 mm, 等效直径为20 μm, 弹性模量为100 GPa, 抗拉强度不低于4 500 MPa, 密度为2 700 kg/m3；束状单丝聚乙烯醇（PVA）纤维, 密度为1 300 kg/m3, 长度为12 mm, 等效直径为20 μm, 抗拉强度为1 830 MPa, 弹性模量为40 GPa.胶凝材料的化学组成见表1.

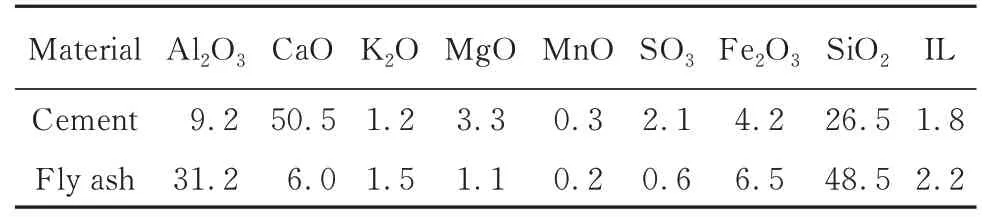
表1 胶凝材料化学组成Table 1 Chemical compositions of cementitiou materials w/%

察尔汗盐湖卤水的pH值为9.60, 采用称量滴定法测试其离子含量, 结果见表2.根据表2, 配制质量浓度为23 g/L的Na2SO4溶液.

表2 察尔汗盐湖卤水中的离子含量Table 2 Mass concentration of ions in brine of Chaerhan Salt Lake mg/kg

设计混凝土的强度等级为C40, 水胶比为0.4, 其m（水泥）∶m（天然河砂）∶m（碎石子）∶m（粉煤灰）∶m（水）∶m（减 水 剂）=400.00∶635.00∶1 165.00∶100.00∶200.00∶0.65.纤维混凝土的纤维体积分数及抗压强度见表3（表中φBF、φPVA分别为BF、PVA纤维的体积分数；φ为混杂纤维BF和PVA的总体积分数）.

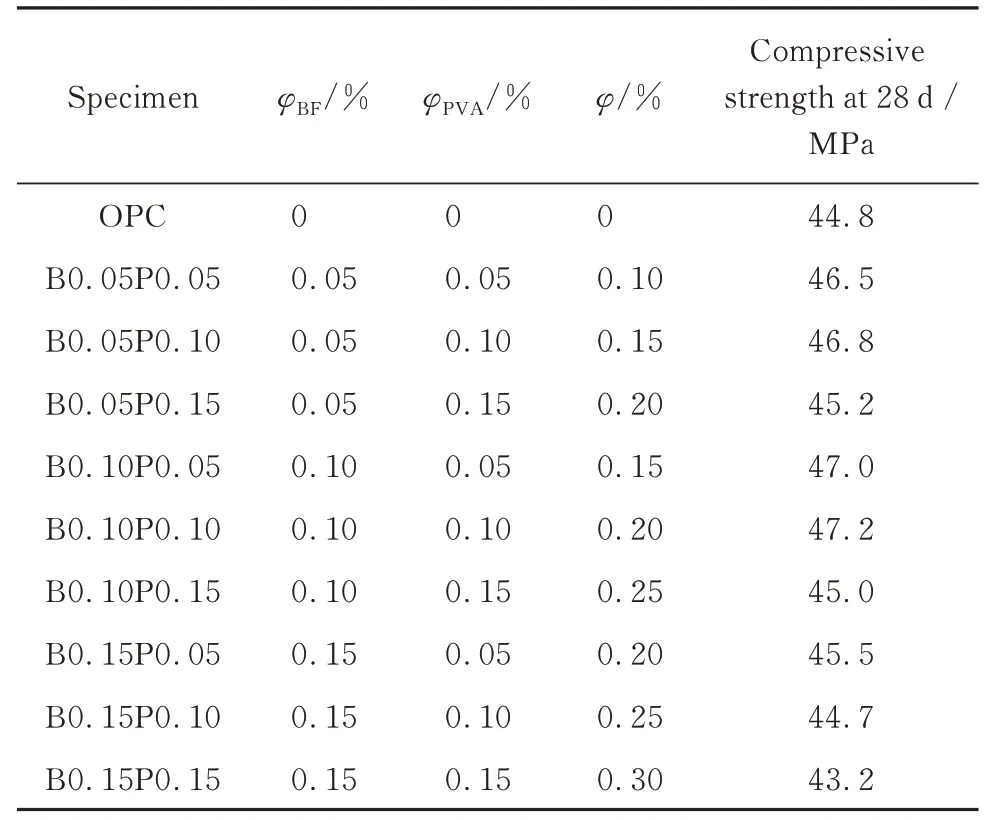
表3 纤维混凝土的纤维体积分数及抗压强度Table 3 Fiber volume fraction and compressive strength of fiber concretes

1.2 试验方法

试件为100 mm×100 mm×100 mm的立方体, 试验流程图见图1.采用YSYW-60型盐水喷雾机, 每隔20次循环测试立方体试件的质量、相对动弹性模量和抗压强度.200次循环（侵蚀200 d）后, 选取OPC和B0.10P0.05的混凝土碎片, 进行SEM测试.

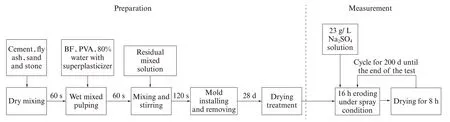
图1 试验流程图Fig.1 Test flow chart

采用耐久性评价参数（抗压耐蚀系数Kf、相对质量评价参数ξ1、相对动弹性模量评价参数ξ2）对混凝土材料在盐雾侵蚀环境中的损伤劣化程度进行评估.当Kf达到75%、ξ1达到5%或ξ2超过40%时, 混凝土材料耐久性失效.评价参数的计算公式为：

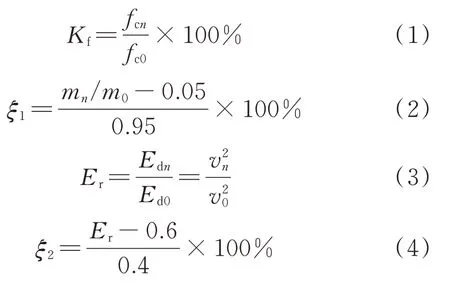
式中：fc0、fcn分别为初始阶段和n次循环后试件的抗压强度；m0、mn分别为初始阶段和n次循环后试件的质量；Er为试件的相对动弹性模量；Ed0、Edn为初始阶段和n次循环后试件的动弹性模量；v0、vn分别为初始阶段和n次循环后试件中的超声波速.

比方咬着小吸管传橡皮筋的游戏，原本应该贴近青春女孩的脸庞，闻到她身上阵阵幽香，感受她吹气如兰，光幻想一下就觉得亢奋。然而现在却是跟臭男生耳鬓厮磨，我猜我和对方都很想死。

2 耐久性结果分析

盐雾侵蚀作用下纤维混凝土抗压耐蚀系数的经时变化曲线见图2.由图2可见：侵蚀200 d时, OPC的Kf降至78.27%, 损伤最为严重；纤维混凝土的Kf早期增长幅度较OPC更大, 且后期下降速率也更低；当φ=0.20%时, 试件的Kf早期增长最为显著, 其中B0.10P0.10在侵蚀80 d时Kf为105.29%, 远高于其他试件；当φ＞0.20%时, 混杂纤维对混凝土Kf的增益效果将大幅度降低, 其中B0.15P0.15在侵蚀200 d时Kf降至80.25%, 仅比OPC高1.98%, 增益效果最差.这和Wang等[8］的试验结果类似, 是由于过高体积分数的纤维不易在混凝土内部搅拌均匀, 容易形成新的缺陷, 难以减缓侵蚀离子对水泥基体造成的损害.

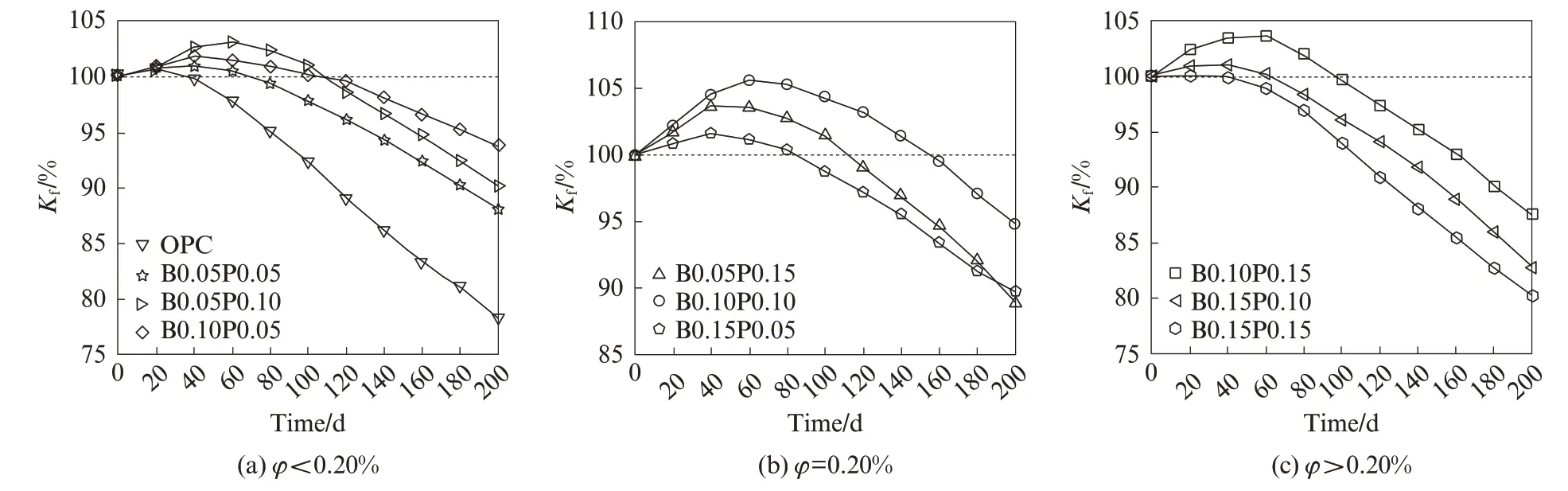
图2 盐雾侵蚀作用下纤维混凝土抗压耐蚀系数Kf的经时变化曲线Fig.2 Time variation curves of Kf of fiber concretes under salt spray corrosion

盐雾侵蚀作用下纤维混凝土相对质量评价参数的经时变化曲线见图3.由图3可见：ξ1波动性很大, 纤维混凝土试件在很长一段侵蚀时间内ξ1均大于100%；OPC的ξ1在侵蚀200 d时为8.85%, 损伤最为严重；B0.10P0.05的劣化趋势远低于其他试件, 侵蚀早期ξ1随侵蚀时间延长不断增大, 在侵蚀80 d时达到峰值151.86%, 远高于OPC.这是由于混凝土内部孔隙中的硫酸盐侵蚀产物具有膨胀性, 产生的张力使水泥剥落, 导致混凝土试件的质量减小[9］, 而纤维可以较好地分担孔隙中积存的膨胀应力, 使得混凝土进一步水化, 密实度持续增加, 纤维混凝土的ξ1得到有效提升.

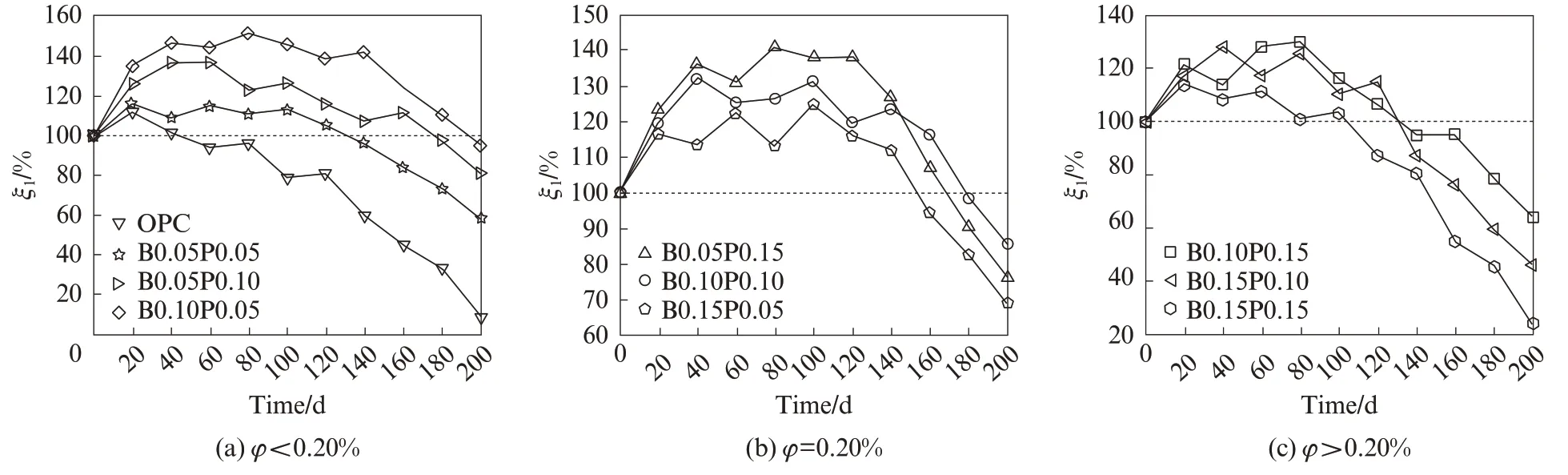
图3 盐雾侵蚀作用下纤维混凝土相对质量评价参数的经时变化曲线Fig.3 Time variation curves of ξ1 of fiber concretes under salt spray corrosion

盐雾侵蚀作用下纤维混凝土相对动弹性模量评价参数的经时变化曲线见图4.由图4可见, 盐雾侵蚀对混凝土ξ2的影响类似于对其对Kf的影响, 均经历了增长和下降2个阶段.乔宏霞等[10］通过Comsol模拟研究表明, 由于盐雾侵蚀环境早期沉积的硫酸盐类晶体提高了混凝土的密实度, 因此其相对动弹性模量有所增加, 且随着侵蚀的不断进行, 生成的膨胀产物和硫酸盐结晶促使微裂缝发展, 最终导致其相对动弹性模量下降.OPC在侵蚀180 d时已经达到失效标准, 而纤维混凝土在侵蚀200 d时仍具有服役能力.侵蚀200 d时, B0.10P0.05的ξ2降至68.15%.此外, 随着混杂纤维体积分数φ的提高, 纤维混凝土ξ2的提升效果逐渐降低.以B0.15P0.15为例, 侵蚀200 d时其ξ2降至0.26%, 已接近耐久性破坏状态, 这表明对混凝土的抗盐雾侵蚀性能, 混杂纤维体积分数存在临界值：当纤维体积分数达到临界值时, 纤维之间可以形成具有最佳搭接长度的三维空间结构, 此时混凝土抵抗盐雾侵蚀的能力最强;当纤维体积分数超过临界值时, 单位体积水泥基体中所分布的纤维数量过多、纤维间距过小,易使相邻纤维发生团聚, 造成薄弱面数量增多, 对纤维混凝土的密实度产生不利影响, 最终导致其抗盐雾侵蚀性能降低.综上, 纤维混凝土中纤维的最佳体积分数为：φBF=0.10%；φPVA=0.05%.

图4 盐雾侵蚀作用下纤维混凝土相对动弹性模量评价参数的经时变化曲线Fig.4 Time variation curves of ξ2 of fiber concretes under salt spray corrosion

由前文可知, 侵蚀200 d后, 出现了部分试件的相对动弹性模量评价参数ξ2＜60%, 而此时其相对质量评价参数ξ1＞95%, 抗压耐蚀系数Kf＞75%.因此,Kf和ξ1只能作为盐雾环境下纤维混凝土耐久性劣化的参考因素, 而由其相对动弹性模量Er所推导出的ξ2可作为关键指标.

盐雾侵蚀200 d后, OPC和B0.10P0.05的SEM照片见图5.由图5可见：OPC表面存在大量多孔结构和爆米花状、短杆状侵蚀产物, 且其分布松散, 并带有大厚度的微裂纹.侵蚀产物大多为钙矾石和石膏：一方面, 此类物质的力学性能不同于水泥水化产物, 这将影响混凝土材料的抗压强度；另一方面, 侵蚀产物会产生不均匀附加应力并作用于混凝土内部, 从而引起较大的膨胀应变, 导致裂缝大量生成, 并造成耐久性损伤.由图5还可见：B0.10P0.05的结构明显比OPC紧密；纤维均匀定向分布在基体中, 形成大量微加强筋；纤维与基体间存在很强的黏结效应, 使应力均匀分散在纤维单丝上, 界面结合强度的提高带来了较大的纤维桥接能力, 从而增强了混凝土的抗压强度, 抑制了裂缝的产生和发展；B0.10P0.05的表面也存在少量钙矾石等侵蚀产物, 但明显可以看出其内部存在致密的水化硅酸钙（C-S-H）凝胶.由此可见, 纤维混凝土对盐雾侵蚀的耐受性比普通混凝土更好.

图5 盐 雾侵 蚀200 d后OPC和B0.10P0.05的SEM照 片Fig.5 SEM images of OPC and B0.10P0.05 after salt spray corrosion for 200 d

3 模型的建立

对混凝土劣化时间的准确预测有助于在建筑工程中作出重要决策, 灰色系统理论已成为解决离散数据、不完全信息及不确定问题的一种有效方法.

假 设X(0)(t)={X(0)(1),X(0)(2), …,X(0)(n)}（n＞0,t为时间序列系数）是不规则分布的原始数据序列, 进行累加生成运算处理后, 得到累加生成序列X（1）（t）：

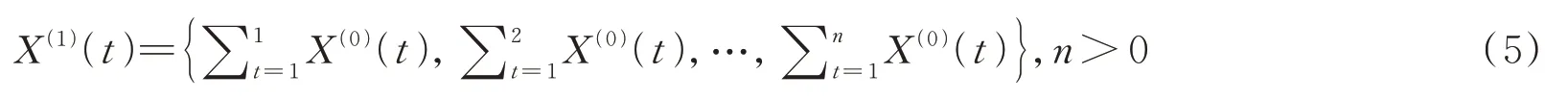
GM（1, 1）模型可用一阶微分方程表示为：

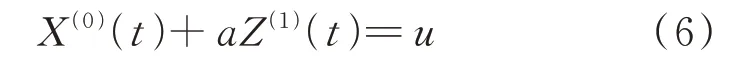
式中：a为发展系数；u为灰色输入系数；Z（1）（t）为关于X（1）（t）的背景值.

将Z(1)(t)=0.5×[ ]X(1)(t)+X(1)(t+1)代入式（6）, 通过拉普拉斯逆变换, 即可得到GM（1, 1）模型的通解为：

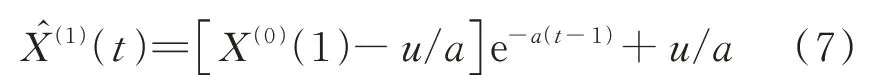
单一GM（1, 1）模型不能将盐雾侵蚀环境下所有影响因素都考虑在内, 当试验数据随机性较大时, GM（1, 1）模型的预测精度并不理想.因此本文将Markov链与GM（1, 1）模型相结合得到GM（1, 1）-Markov模型, 以提高预测精度.GM（1, 1）-Markov模型首先通过计算得到GM（1, 1）预测值和原始数据之间的残差, 并建立序列预测模型；然后利用Markov转移矩阵判断残差的转移行为；最后根据修正后的残差得出GM（1, 1）-Markov预测值.

由于残差预测模型的推导步骤与GM（1, 1）模型推导过程相似, 详细计算过程参考文献[11］, 其结果如下：

对于残差中存在的一些规律性信息, 可建立Markov转移矩阵规定其状态：残差是正数时为状态1；负数时为状态2.根据状态的正负性可得到状态转移概率Pij：

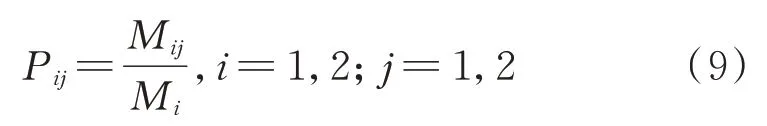
式中：Pij是从状态i到状态j的转移概率；Mij是从状态i到状态j的过渡时间；Mi是属于第i个状态的数据数量.

由状态转移概率可得到状态概率转移矩阵P：

最终可获得GM（1, 1）-Markov模型计算结果及预测值

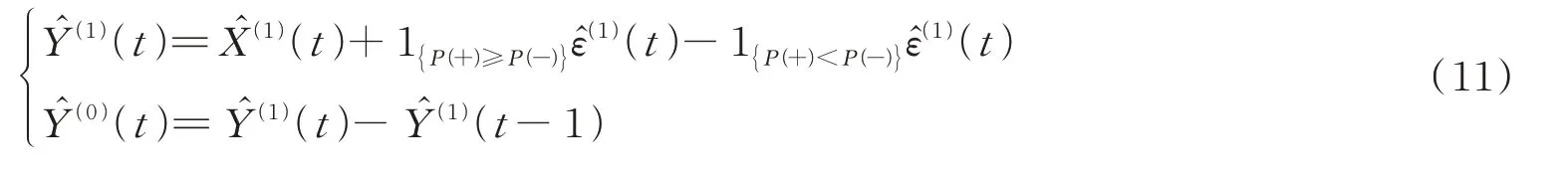
4 预测结果分析

以耐久性能较好的B0.10P0.05为例, 用GM（1, 1）、GM（1, 1）-Markov模型分别对其相对动弹性模量Er进行预测, 当Er＜0.6时, 认为达到该混凝土的寿命.GM（1, 1）、GM（1, 1）-Markov模型拟合结果见图6.由图6可见：Markov的引入明显提高了GM（1, 1）模型的预测精度；GM（1, 1）-Markov模型能够较好地匹配试验数据的波动性变化, 其拟合值的相对误差整体上明显低于GM（1, 1）模型.

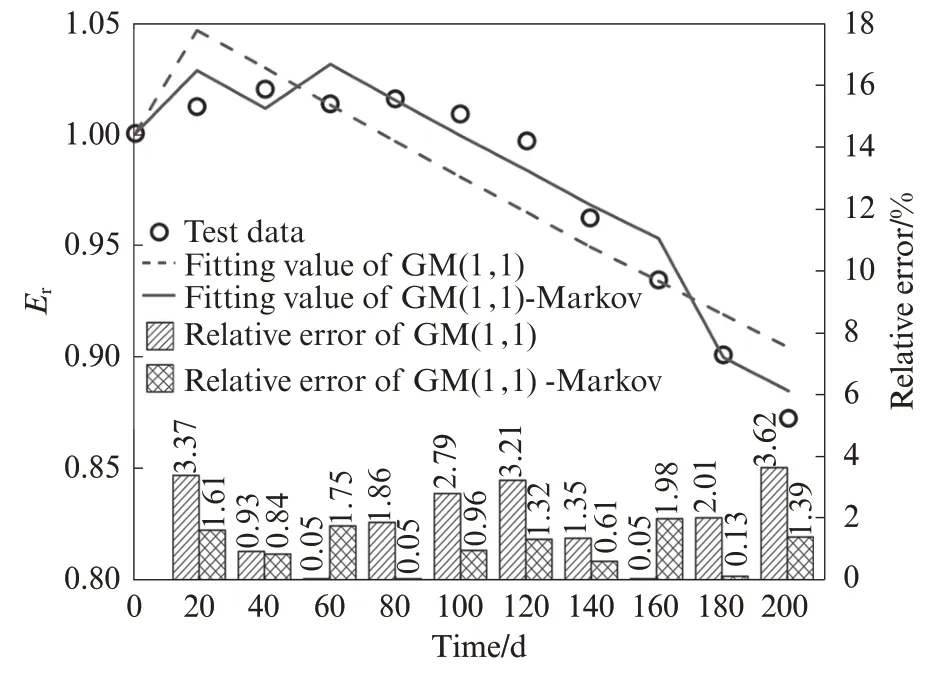
图6 B0.10P0.05的GM（1, 1）、GM（1, 1）-Markov模型拟合结果Fig.6 Model fitting results of GM（1, 1）and GM（1, 1）-Markov of B0.10P0.05

准确预测纤维混凝土的寿命, 将有助于提前对处于盐雾侵蚀环境中的纤维混凝土进行检测和维护.为了进一步了解其他配合比纤维混凝土的劣化趋势, 通过GM（1, 1）-Markov模型对其Er进行预测, 结果如图7所示.由图7可见：在侵蚀180 d时, OPC遭到破坏, 这和试验过程中Er的数据相吻合, 侧面印证了GM（1, 1）-Markov模型具有很高的预测精度；侵蚀220 d时, B0.15P0.15达到失效标准, 即当纤维总体积分数达到0.30%时, 纤维对混凝土耐久性能的提升效果显著降低, 这说明尽管混掺BF和PVA纤维可以提高混凝土在盐雾环境中的服役寿命, 但纤维总体积分数不宜过多；盐雾侵蚀环境下耐久性能最好的为B0.10P0.05, 其服役时长为680 d, 远超其他试件.

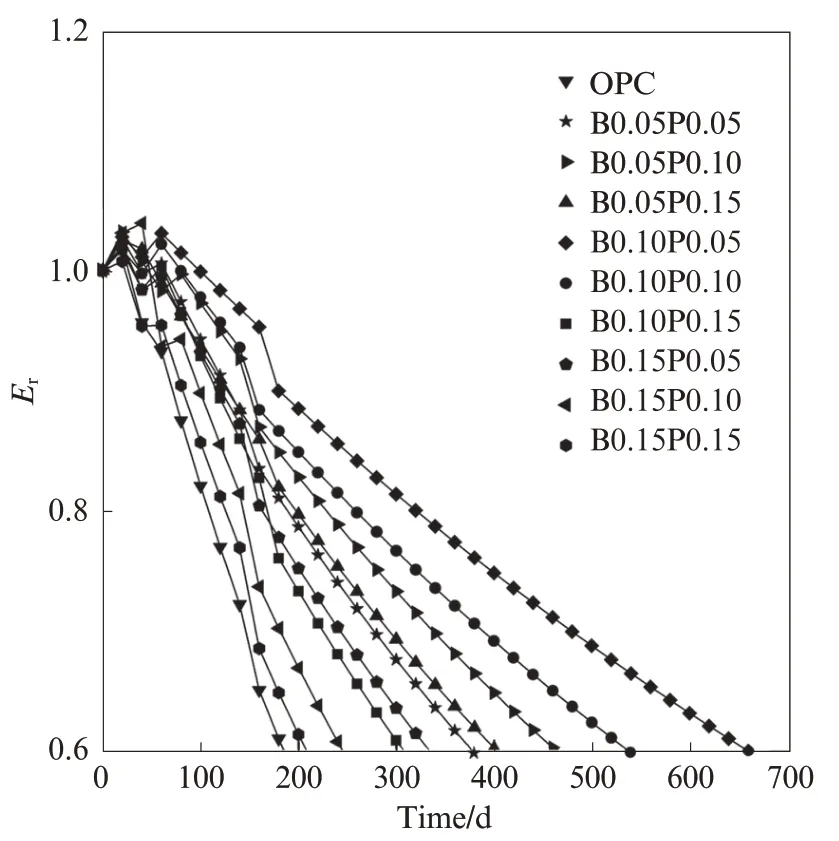
图7 基于GM（1, 1）-Markov模型预测混凝土的相对动弹性模量Fig.7 Prediction of Er of concrete based on GM（1, 1）-Markov model

5 结论

（1）盐雾侵蚀加速试验中的侵蚀溶液质量浓度参考了察尔汗盐湖卤水中SO2-4的质量浓度, 较好地还原了西部盐湖地区混凝土材料的破坏过程, 明确了混掺玄武岩纤维和聚乙烯醇（PVA）纤维对混凝土在该地区耐久性能显著提升的可行性.

（2）在盐雾环境下, 纤维混凝土的抗压耐蚀系数Kf先上升后下降, 相对质量评价参数ξ1波动性较大, 相对动弹性模量评价参数ξ2可作为评价纤维混凝土损伤劣化的决定性因素.混掺纤维可以延缓SO2-4对混凝土内部的侵蚀速率, 从而提高混凝土的抗盐雾侵蚀能力.

（3）将相对动弹性模量Er作为关键劣化因素, 所建立的GM（1, 1）-Markov模型与实测数据吻合较好, 能够有效预测纤维混凝土的损伤劣化趋势.当玄武岩纤维体积分数为0.10%、PVA纤维体积分数为0.05%时, 纤维混凝土在盐雾环境中的耐久性能最佳, 可服役时间达到680 d.当纤维的总体积分数达到0.30%时, 纤维对混凝土耐久性能的提升效果显著降低.