基于改进RRT*算法的移动机器人路径规划研究*

印 峰，谢青松

(湘潭大学 自动化与电子信息学院，湖南 湘潭 411105)

0 引言

移动机器人路径规划研究的目标是在具有障碍的环境中，在满足不发生碰撞的条件下搜索，依据路径和时间最短原则，搜索一条从起始点到目标点的最优可行路径[1-2].目前路径规划研究的主要方法[3]有A*算法[4]、Dijkstra算法[5]、人工势场法[6]和快速探索随机树(RRT)算法[7]，以及渐进最优快速随机搜索树(RRT*)算法.其中RRT的主要思想是从起始点开始随机生成一个树状的网络图，通过迭代地探索一系列中继点(即父节点)，最终形成一条到达目标点的可行路径.传统的RRT算法不具有目标导向特性，其搜索路径过程具有较强的随机性，针对这个问题，Karaman等[8]提出了一种具有目标导向型的渐进最优快速随机搜索树RRT*算法，其原理是通过对父节点进行优化选择以提高原有RRT算法的搜索效率.通过改变父节点选择的方式，采用代价函数来选取拓展节点范围内最小代价节点为父节点，同时，每次迭代后都会重新连接现有树上的节点，保证计算以渐进方式探索到最优解.

为了优化节点，RRT*算法是采用高斯采样策略，由于摒弃的随机节点中有可能包含了当前的最优节点，因此算法无法保证通过计算代价最小值的方式来获得当前最优节点.同时，由于搜索最优父节点的过程需要多次迭代计算，这无疑降低了整体规划的时效性.针对上述问题，研究者对RRT*做出了一系列的改进工作.Gammell等[9]提出的Informed-RRT*算法，通过引入空间约束以减少冗余节点的数量，降低搜索过程的随机性.但是，该方法花销的时间仍然过长，目前仅适用于狭窄区域的路径搜索[10-12].

针对上述问题，本文提出了一种基于RRT*的改进算法，其主要思想是应用动态步态延伸帮助RRT*算法找到更优的潜在父节点集，然后结合一种新颖的类三维地图中的驻点信息，在可行的范围内确定最优的父节点，从而实现更为高效的路径规划过程.为了验证本文文法的有效性，从路径长度以及时间性能两个方面，对比了本文方法和最新的Informed-RRT*算法.

1 研究的理论基础

1.1 RRT算法

RRT算法是一种随机采样方法，它可以是在二维空间甚至是在三维空间中都很有效的规划方法，RRT算法从起始点出发，通过对未知空间以随机采样的方式增加子节点，最终生成一个随机扩展树，当随机扩展树中的子节点含有目标点时，则生成一条从初始点到目标点的目标路径，RRT算法扩展方式如图1所示.

RRT算法以Xinit为出发点进行扩展，在陌生环境随机选取一个采样点Xrand，然后选取距离该采样点最近的一个节点Xnear，在Xnear和Xrand的连线上以固定区间的步长ε选取一个新的采样点Xnew.如果当前的采样点Xnew没有与已知的障碍物发生碰撞，那么将采样点Xnew加入随机树中，反之则将该采样点舍弃，并重新选取采样点Xrand进行扩展.重复以上步骤直到扩展树找到一条从Xinit到Xgoal的无碰撞路径.

1.2 RRT*算法

研究表明，RRT算法仍存在许多有待提升的空间[13].例如对于特点形状的应用场景(例如狭窄通道)，RRT算法收敛速度会有较明显的下降.针对该问题，文献[14-15]在RRT算法上提出了一种改进的RRT*算法.后者重新定义了父节点的搜索方式，对父节点采取一种导向式的引导.相较于RRT算法，RRT*算法最大程度保留了RRT算法的概率完备性，由于采用了父节点引导机制，同时提高了算法的收敛速度，使得可以以更少的迭代生成更优的路径，提高了规划的效率.RRT*路径的扩展方式如图2所示.

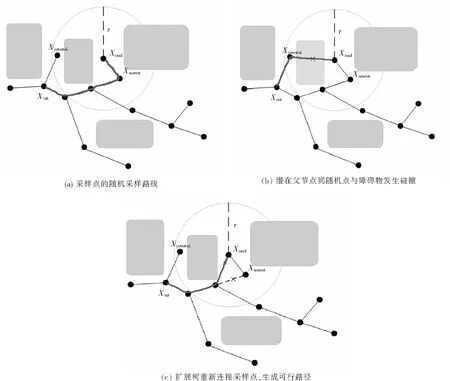
图2 RRT*的可行路径扩展示意图Fig.2 Schematic diagram of feasible path extension for RRT*

RRT*算法首先产生一个随机点Xrand，然后基于RRT算法找到随机树上距离Xrand最近的一个节点Xnearest并与之相连.以Xrand为中心，r为半径，在随机树上搜索潜在父节点Xpotential，通过碰撞测试计算路径代价，并与之前的路径做比较，选取代价较小的节点为最新父节点，切断之前较长的路径并更新，直到扩展树到达目标点为止.

1.3 类三维地图

类三维地图是在普通的二值栅格地图上人为地按照一定规则添加高度值，使其在路径规划中不需要借助其他信息即可通过障碍物本身的高度信息就可以完成部分避障工作.

在文献[16]中将位于障碍物范围内高度值最高的点定义为起点，之后垂直于这个路径内的箭头方向为下降方向，同时将修正路径段到被修正路径段中最大的点定义为一个犄角点，而位于路径同一侧中距离这段路径最远的犄角点则定义为驻点，驻点的详细寻找图如图3所示.

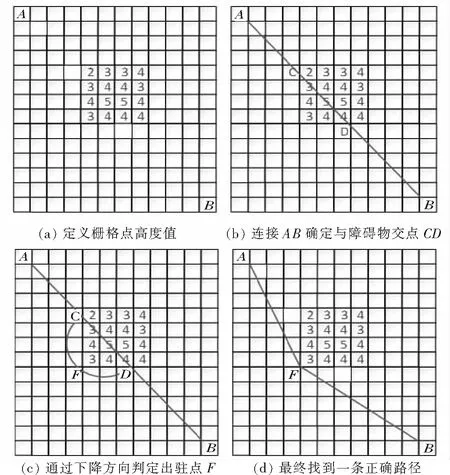
图3 类三维地图驻点以及路径寻找方式Fig.3 Three-dimensional-like map stationary point and path finding way

首先先确定起始点A和目标点B，假设要从A点运动到B点，需要经过中间一大片障碍物，对于自由区域所有栅格点的高度值都赋值为0，然后定义高度值大于1的点，之后对于障碍物赋予坐标中的最大值以及最小值，并对所有栅格点的高度值赋予1，对于最大点附近的栅格点依次减1，同时对最小点附近的栅格点依次加1，连接AB两点经过障碍物与障碍物接触点分别定义为CD两点，如图3上的弧线，CD两点之间可以进一步优化为折线，从下降方向判定可以得知F点为驻点，连接AFB即为最短路径.

由于类三维地图中驻点定义的特殊性，可以依据驻点的定义加入新算法中，RRT*算法定义的父节点是以Xrand为半径的范围内确定的，当加入驻点定义到新算法中，依据驻点的定义是根据路径箭头方向为下降方向，其具有一定的目标偏向性，如果此时再以驻点为中心去搜索新的潜在父节点，则相比于RRT*算法搜索的潜在父节点会更具有目的性.

2 RRT*算法改进

2.1 算法设计原理

RRT*采用渐进最优的路径搜索模式，在潜在父节点的选取时会产生大量无用的结点，造成其计算量随着样本的数量增加而急剧增加，为了减少冗余节点的数量，本文首先基于RRT*算法的采样模式进行初采样；然后，以提取的类三维地图中驻点为中心，在一定的半径范围内寻找潜在父节点，通过具有目标偏向目标的搜索可以得到更为理想的潜在父节点，进而减少路径长度和规划时间.为了便于描述，将改进算法记为Class3D-RRT*算法.

RRT*随机点采样模式为高斯采样，具有在一定小范围内采样多个点并选择最优点的特征.与之相比较， Class3D-RRT*算法不仅可以具有偏向目标方向的作用，而且可以有效缩小搜索父节点的范围，使其在选取父节点时相比于原算法具有更强的导向性.而使用了更为合适的潜在父节点可以得到更优的规划结果.

Class3D-RRT*算法的详细步骤如图4所示.

图4 算法示意图Fig.4 Schematic diagram of algorithm

首先以潜在父节点为中心，Rp为半径，在其半径范围内做下降方向去搜索驻点，同时以驻点为中心，Rh为半径，从该半径范围内去搜索潜在的父节点，当搜索到潜在父节点时连线，同时以当前潜在父节点为中心继续寻找下一个驻点，如未寻找到，则依据RRT*算法寻找潜在父节点并连线，最终通过此方法搜寻到一条从初始点到目标点的路径.下面为算法的详细步骤以及算法实现.

2.2 算法实现

在确定父节点时，搜索树探索到各个节点，以r为半径搜索最近的一个节点Xnearest，通过碰撞测试并与原路径相比较，若所得新的路径更近，则将Xnearest记为Xpotential-parent，然后，设搜索树T=(V,E)，以Xpotential-parent为中心，记坐标为(Ix,Iy)为Rp的球形空间Bpotential-parent，此时：

S(Xpotential-parent，T，Rp)={v∈V；v∈Bpotential-parent}，Xstagnationpoint⊆V.

(1)

式中，S表示驻点的集合.

半径r为：

(2)

式中：δ为常数；v为节点集合；Num(v)为集合v中所有节点的数目；n为配置空间维度，此时此刻r随着节点数的增大减小，而此时球形空间Bpotential-parent的半径Rp亦等于r.

当确定最佳潜在父节点时，判断下降方向，若此时下降路径穿过了某个障碍物，则定义位于障碍区域路径下降方向一侧的点(Iy，Jy)，其值满足下式：

(3)

式中：k=Im1-In1/Jm1-Jn1，(Im1，Jm1)是当前穿过障碍物路径的起始点坐标，(In1，Jn1)是当前穿过障碍物的终点坐标，(Iam，Jam)是当前障碍物最大的坐标点.在确定下降方向后，再寻找当前犄角点.在规划实施过程中，将修正路径段到被修正路径长度距离最大的点定义为犄角点，此时修正路径段上的点(Iy，Jy)与被修正路径段的距离为h=s/2c，其中：

(4)

(5)

(6)

(7)

(8)

式中：(Iy，Jy)为修正路径段上的点坐标；(Im2，Jm2)为被修正路径段上的起点坐标；(In2，Jn2)为被修正路径段的终点坐标.在获取不同障碍物的犄角点后，再从中选取驻点，应当选择路径同一侧距离这段路径最远的犄角点为驻点.此时以驻点为中心，Rh为半径，并且令Rh=Rp，在半径范围内选取最佳潜在父节点，直至到达目标点为止.算法的主要计算步骤如下：

步骤1：将当前的普通地图转换为类三维地图并产生一个随机点Xrand.通过随机点Xrand生成一个随机树,并在其中找到与Xrand最近的一个节点Xnearest.

步骤2：以Xrand为中心，Ri为半径，在节点树中对当前的Xnearest进行碰撞测试，如果此时Xnearest穿越到了栅格点大于0的点则定义为穿过障碍区域.

步骤3：如果此时可以通过碰撞测试，并通过计算相对于原先路径更近，则可以成为当前的Xpotential-parent.

步骤4：以Xpotential-parent为中心，Rp为半径，作下降方向，若路径穿过某个障碍区域，则依据类三维地图法犄角点的定义去确定犄角点，再依据相对距离进而判断驻点，若未穿过，则定义目前的Xpotential-parent转变为新的Xinit，重新产生随机点Xrand并重复上述步骤.

步骤5：当确定驻点Xstationary point时，以此点为中心，Rh为半径，在该半径范围内寻找下一个潜在父节点，之后应用原RRT*算法继续搜索下一个潜在父节点，直到找到一条从初始点到目标点的路径.

图5给出了本文算法主要步骤的图示过程.

图5 Class3D-RRT*路程图Fig.5 Class3D-RRT* road map

3 实验仿真与分析

3.1 单障碍物地图构建

为了验证Class3D-RRT*的性能，本文在pycharm社区版中进行相关测试实验，并将RRT*算法、Informed-RRT*算法以及Class3D-RRT*的规划结果进行了对比.本实验分别在单障碍物地形和多障碍物地形情况下进行实验仿真，计算机处理器采用Intel-i7 11800H，内存16 GB.

首先是对单障碍物地形情况进行模拟，在单一障碍物中计算出的路径时间进行比较，起始点在(0,2)，目标点在(8，8).图6为单障碍物环境路径对比图.图中，圈代表圆形障碍物，线为实际算法运算路径.

图6 单障碍物情况地图路径对比Fig.6 Map path comparison for single obstacle case

如表1所示，在单障碍物地图的仿真过程中，通过实验结果得知，本文算法相对于RRT*算法以及Informed-RRT*算法，平均路径更短，平均耗时也更短.

表1 单障碍物地图仿真实验数据对比

3.2 多障碍物地图应用

在多图形障碍物的复杂情况下，多障碍地图1的初始点坐标为(4，5)，目标点坐标为(14，10)，多障碍地图2的初始点坐标为(0,2)，目标点坐标为(10，10)，多障碍地图3的初始点坐标为(0，2)，目标点坐标为(14，10).图7、8、9所示分别为在多障碍环境地图1、2、3中，同方法规划路径的实验结果对比.图中的圆圈或者方块代表障碍物.

图7 多障碍环境地图1中规划路径对比Fig.7 Comparison of planned paths in Multi-obstacle environment Map 1

图9 在多障碍环境地图3中规划路径对比Fig.9 Comparison of planned paths in Multi-obstacle environment Map 3

如表2所示，在多障碍物地图的三组仿真实验中，第一组与第二组多障碍物地图仿真实验中，只有单一样式不同大小的障碍物，第三组实验中同时有样式不同、大小不一的障碍物，无论是对比平均路径长度还是平均耗时来看，本文算法更优.

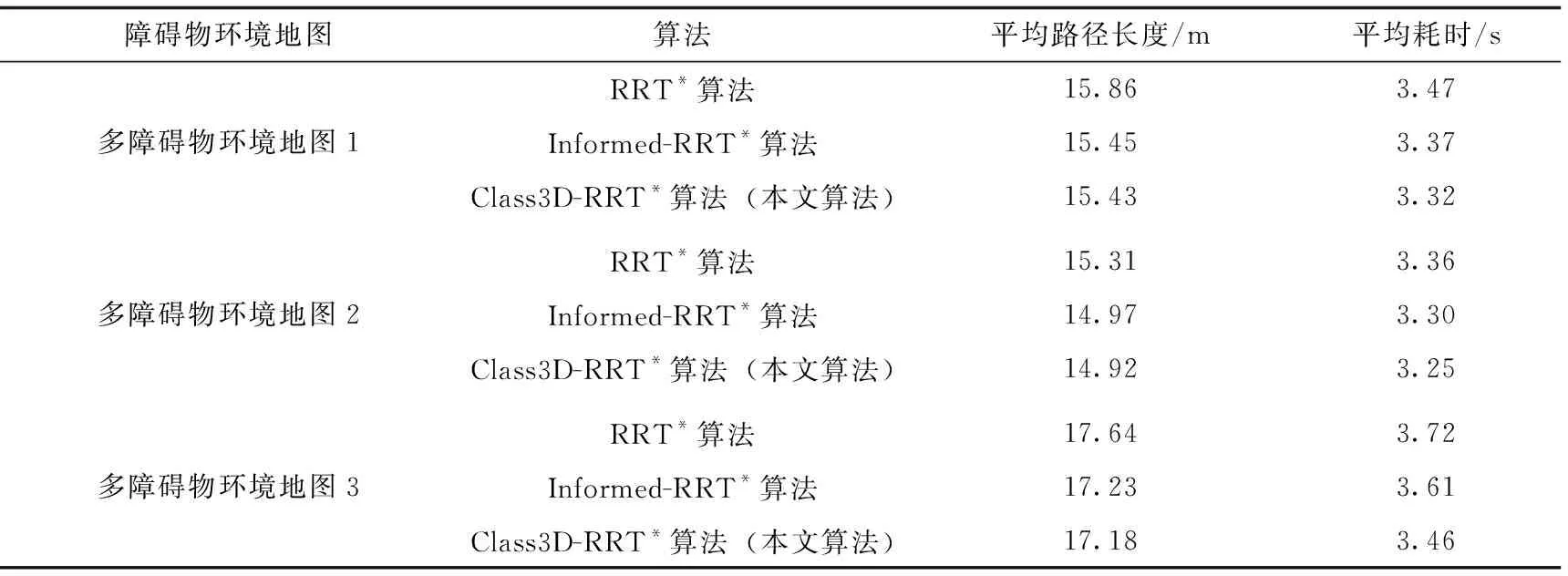
表2 多障碍物地图仿真实验数据对比

4 结束语

本文的主要目的是为了路径更优同时也是为了正确地避开障碍物，以尽量最短的路程规划从初始点到达目标点，本文提出了一种Class3D-RRT*算法，其主要方法是在搜索到潜在父节点后，在其半径范围内搜索是否有驻点，依据驻点在此范围内寻找下一个父节点，这样更具有目的性，使用新的改进算法在简单以及复杂的障碍物中反复进行仿真实验，最终的仿真结果也表明新的改进方法可以更加有效地选择更优父节点，进而使得路径规划的路程更短，时间更优.