非线性SMA调谐质量阻尼器信息化建模仿真分析

王桂玲

(中铁二十局集团有限公司 陕西西安 710016)

1 引言

调谐质量阻尼器(Tuned Mass Damper，TMD)是一种利用子结构(控制装置)与主结构(受控结构)共振以吸收并耗散振动能量的被动减振装置。TMD由于具有减振效果显著、构造简单、无需外部能源供给以及造价低廉的优点，在工程实践中得以广泛应用[1－3]。更多关于TMD介绍、发展及工程应用内容可参考综述文献[4－6]。

研究发现，传统的线性TMD是一种窄带控制器，仅能有效抑制如风荷载和交通荷载等窄带激励引起的振动。当遇到地震、冲击荷载等宽带激励时，线性TMD控制效果有限[7－8]。此外，文献[9]指出:线性TMD与受控结构间的质量比要达到5%～8%才能在地震作用下发挥作用。较高的质量比也限制了其在工程结构减振控制中的应用。近年来，为了提高传统线性TMD在结构地震响应控制中的适用性，非线性TMD应运而生。非线性TMD和线性TMD的区别主要在于提供恢复力的方式不同。非线性TMD的恢复力通常是由碰撞相互作用[10]、非线性运动轨道(非线性能量阱)、非线性－线性联合刚度以及非线性弹簧等方式提供，其恢复力中没有或仅有非常弱的线性项，这保证了非线性TMD具有较宽的减振频率带宽。超弹性形状记忆合金(Shape Memory Alloy，SMA)是实施结构振动控制的理想材料。在外部荷载作用下，超弹性SMA会发生应力诱发马氏体相变，其力－位移曲线表现出明显的迟滞效应。此外，其力－位移迟滞环可以提供优越的耗能性能。因此，可以直接使用超弹性SMA元件代替线性弹簧，以提高传统线性TMD的减振性能。

本文依据TMD的工作原理并结合SMA元件，研发一种新型非线性SMA调谐质量阻尼器(Nonlinear SMA tuned mass damper，N-SMA-TMD)，并将其应用于地震激励下单自由度结构的响应控制。首先，介绍新型N-SMA-TMD的设计与减振机理；然后，采用等价线性化方法，建立适用于结构动力分析的SMA简化折线模型；最后，通过对比分析线性TMD控制单自由度结构和N-SMA-TMD控制单自由度结构在地震激励下的动力时程响应计算结果，阐明N-SMA-TMD相比于传统线性TMD的优势所在。

2 非线性SMA调谐质量阻尼器设计与减振机理

2.1 非线性SMA调谐质量阻尼器的设计

针对传统线性TMD的不足，本文基于TMD的减振机理和超弹性SMA元件的滞回耗能特性，设计出如图1所示的新型N-SMA-TMD。考虑减振系统不需要SMA元件提供承载力，在设计装置时，选用了刚度较低但变形能力更强的SMA螺旋弹簧作为核心部件。

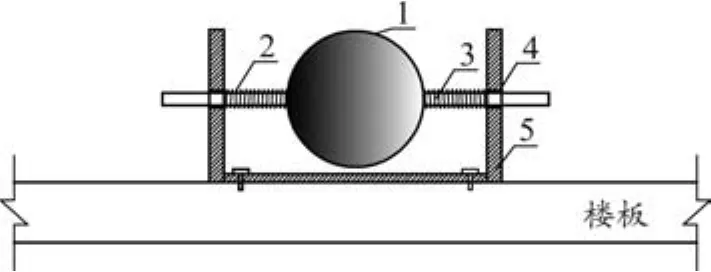
图1 非线性SMA调谐质量阻尼器

新型N-SMA-TMD由金属圆球质量块1、SMA螺旋弹簧2、定向导杆3、滑动支座4、箱形支架5组成。金属圆球质量块1两侧与定向导杆3固定连结，以控制质量元件沿固定方向运动；定向导杆3外侧设置SMA螺旋弹簧2，通过改变金属圆球质量与SMA螺旋弹簧初始刚度的比值，实现装置与结构间的调谐；箱形支架5与定向导杆3通过滑动支座4连接，以减小定向导杆与箱形支架间的摩擦力，实现近似光滑的设计。

2.2 非线性SMA调谐质量阻尼器减振机理

新型N-SMA-TMD均属于被动控制装置，当主结构受到外部地震激励作用时，装置内的质量元件随着主结构晃动发生反向共振，将地震输入能量传递给装置，抑制主结构的地震响应。此外，SMA元件在随质量元件运动过程中，由于马氏体相变被激活而进入非线性阶段并开始耗散输入能量。该新型N-SMA-TMD以SMA为核心滞回耗能元件，在吸振的同时能够将能量耗散，实现双重减振控制效果。在具体应用过程中，可将N-SMA-TMD通过螺栓和箱形支架固定于结构内的楼板上，根据不同的减振控制目标，在结构内部设计不同安装位置和摆放方位的组合设置方案。

3 SMA等价线性化模型

为进行动力时程响应分析，需建立描述SMA超弹性的力学模型。作为一维宏观唯象本构模型的典型代表，Graesser-Cozzarelli(G-C)模型因形式简单且定义了适用于工程计算的参量体系，而在结构振动控制领域得到了广泛应用。G-C模型具体表达式为:

式中:各参数意义参考文献[11－12]；FSMA和xSMA分别为SMA提供的恢复力和位移，其与SMA应力及应变转换关系为:

式中:A为SMA元件横截面总面积；l为SMA元件总长度。

为便于对地震作用下SMA减振结构的动力反应进行分析，将SMA恢复力等效分解为如图2所示的弹性力和滞变力，即:

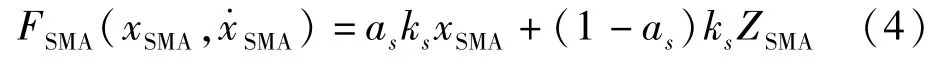
式中:FSMA(xSMA，SMA)为超弹性SMA产生的恢复力，括号内参数是SMA产生的恢复力与SMA位移和速度相关的函数。

等式右边第一项为弹性力，其中:as为屈曲后刚度系数；ks为弹性模量。等式右边第二项为滞变力，其中:ZSMA为滞变位移，不同的滞变恢复力模型主要表现在滞变位移的不同。

任文杰[13]建议使用如下折线型模型来描述超弹性SMA的滞变位移:

式中:ua和ub对应图2中a点和b点的位移值；sign(xSMA)为符号函数，其具体表达式为:

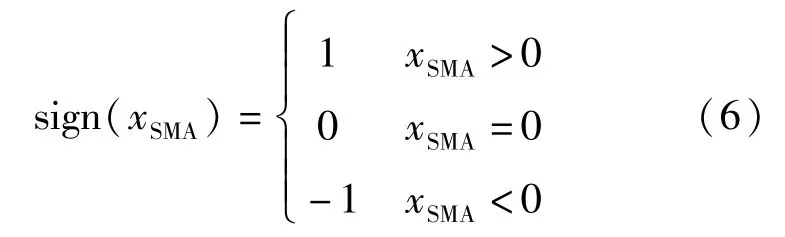
图2 SMA恢复力等效分解示意

为了验证上述SMA折线型模型的正确性，通过Matlab中Simulink模块对其进行数学仿真。图3为0.1 Hz频率、16 mm(折线模型和G-C模型)及12 mm(折线模型)位移幅值加载条件下，G-C模型和折线型模型求得的SMA滞回曲线。G-C模型仿真材料参数为[14]:Ea＝1.0×104N/m，fT＝0.15，Fms＝25 N，ha＝0.019 7，n＝3，a＝2 500，c＝0.001；折线型模型仿真材料参数为:as＝0.01，ks＝1.25×104N/m，ua＝0.4 mm，ub＝2.05 mm。由图3可知，折线型模型可以较为准确地描述超弹性SMA的本质特性，通过选取合适的材料参数可以模拟出超弹性SMA迟滞“旗形”曲线，可以将折线型模型当作G-C模型的简化版本。此外，本文仿真结果与Yan和Nie[15]得到的仿真结果也相符合。

图3 SMA折线型模型与G-C模型比较

4 非线性SMA调谐质量阻尼器的减振效果

4.1 结构动力响应计算模型

通过计算N-SMA-TMD控制结构在输入地震波作用下的时程响应，验证N-SMA-TMD的有效性，并进一步通过与传统线性TMD控制结构计算结果进行对比，阐明N-SMA-TMD相较于传统线性TMD的优势所在。

N-SMA-TMD单自由度结构系统在地震激励作用下的运动方程为:

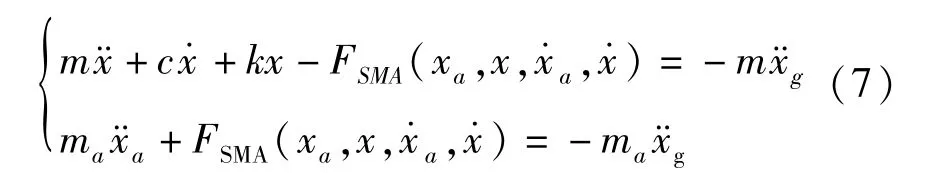
式中:xa和x、与、及分别为N-SMA-TMD和主体结构相对于地面的位移、速度、加速度；m和ma分别为主体结构和N-SMA-TMD的质量，取值为10×103kg和250 kg；c和k分别为主体结构的粘滞阻尼系数和刚度，取值为0.03 和1.75 ×104N/m；为地面运动加速度。

SMA元件产生的恢复力由FSMA(xa，x，，)给出，参数取值和第3节相同。括号中各参数为影响恢复力大小的因素。

4.2 TMD的参数优化

为比较N-SMA-TMD和线性TMD的减振性能，分别对附加N-SMA-TMD和线性TMD的单自由度结构进行动力时程分析。TMD的最优固有频率比和最优阻尼比通过Den Hartog模型的固定点理论求得，具体求解公式为:

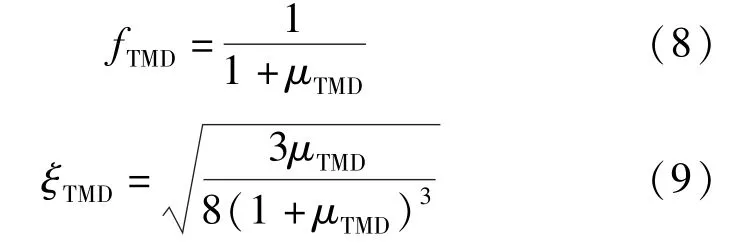
式中:fTMD为线性TMD最优固有频率比；ξTMD为线性TMD的最优阻尼比；μTMD为质量比。

附加TMD的单自由度结构参数与4.1节相同。Christoph和Thomas指出:线性TMD减振装置与受控结构间的质量比要达到5%～8%才能在地震作用下发挥作用。本文将线性TMD减振装置的质量比定为8%，其质量为250 kg，频率为3.878 5，阻尼比为16.67%，线弹簧刚度为1.203×104N/m。

4.3 地震时程响应分析

本文选取EL-Centro波和Traft波作为地震动输入，调整两条地震波的加速度峰值为400 gal。图4为两条地震波作用下无控结构(S-UC)、TMD控制结构(S-TMD)和N-SMA-TMD控制结构(S-N-SMATMD)的动力时程响应计算结果。由图4可以看出，TMD减振控制效果不稳定，在EL-Centro波和Traft波作用下，结构的动力响应甚至可能被放大。例如，在EL-Centro波作用下，附加TMD结构在5.2 s的位移响应由8.79 cm增大至11.06 cm；在Traft波作用下，附加TMD结构在7.02 s的位移响应由6.98 cm增大至13.41 cm。而N-SMA-TMD的减振控制效果较为稳定，在不同地震波作用下N-SMA-TMD均可以有效降低结构的位移响应和加速度响应。

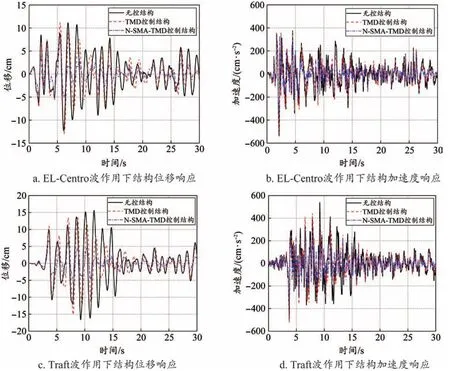
图4 不同地震波作用下结构响应

为更加直观展现TMD和N-SMA-TMD的减振效果，表1列出了在两条地震波作用下附加TMD和N-SMA-TMD结构的位移和加速度响应，包括其峰值和均方根值。由表1可知，TMD可以有效降低结构的加速度峰值响应，但位移峰值响应控制效果不稳定。例如，EL-Centro波作用下，结构的峰值位移响应由－12.40 cm被放大至－12.95 cm；在TMD的控制下，结构位移响应均方根和加速度响应均方根均有所降低；尽管N-SMA-TMD的减振效果与地震动输入有一定关联，但结构响应的峰值和均方根值均得到了有效控制。此外，相比于TMD，N-SMA-TMD的减振效果更为稳定、有效。例如在EL-Centro波作用下，结构的位移响应均方根和加速度响应均方根分别由4.16 cm和107.50 cm/s2降至1.75 cm和73.42 cm/s2；而在传统TMD控制下，响应的均方根分别为3.64 cm和96.11 cm/s2。

图5为SMA元件和普通线弹簧在两条不同地震波作用下的恢复力输出曲线。由图5可知，在不同地震波激励下，SMA元件的位移值均小于普通线弹簧，这说明SMA元件可以显著降低质量振子的位移值。此外，SMA元件相比于普通线弹簧具有更加优良的减振控制效果。这是因为SMA元件在振动过程中发生了应力诱发马氏体相变，进而导致力－位移曲线表现出明显的非线性迟滞特征，耗散了地震能量。SMA元件的非线性迟滞循环效应可以提供更宽的频带，相比于普通弹簧在振动控制方面更具优势。

图5 线弹簧和SMA恢复力曲线

5 结论

本文依据TMD工作原理并结合SMA元件，研发了一种新型非线性SMA调谐质量阻尼器，并将其应用于地震激励下结构的响应控制。对比线性TMD控制结构和N-SMA-TMD控制结构在地震激励下的动力时程响应计算结果，得到的结论如下:

(1)相比于TMD，N-SMA-TMD的减振效果更为稳定、有效。在 EL-Centro波作用下，N-SMA-TMD控制结构的位移响应均方根和加速度响应均方根分别由4.16 cm和107.50 cm/s2降低至1.75 cm和73.42 cm/s2；而在传统TMD控制下，响应的均方根分别为3.64 cm和96.11 cm/s2。

(2)考虑SMA元件在振动过程中发生了应力诱发马氏体相变，进而导致力－位移曲线表现出明显的非线性迟滞特征，耗散了地震能量。SMA元件相比于普通线弹簧具有更加优良的减振控制效果。

(3)SMA元件可以显著降低质量振子的位移值，提高减振装置的适用性。SMA元件的非线性迟滞循环效应可以提供更宽的频带，相比于普通弹簧在振动控制方面更具优势。