幂零奇点小邻域内相轨线的拓扑结构与中心问题

李锋，张冬梅 ，窦霁虹

(1.临沂大学数学与统计学院，山东 临沂 276005;2.西北大学数学学院，陕西 西安 710127)

1 引言

近年来，关于平面多项式问题的中心焦点判定问题受到了国内外学者的广泛关注，其主要方法仍然是后继函数法，形式级数法，平均法，等等.但是对于退化奇点，由于经典的方法不再适用，相关问题的研究进展一直较为缓慢.作为一类特殊的退化奇点，幂零奇点的研究也一直吸引着众多学者的目光.当一个以坐标原点为孤立奇点的实平面微分自治解析系统在原点邻域的线性近似系统有两个零特征根，但线性项的系数不全为零时，该系统的坐标原点称为幂零奇点.考虑原点为幂零奇点的实平面微分自治系统

其中X(x，y)，Y(x，y) 在原点邻域解析.

设y=f(x)是隐函数方程

在原点邻域的唯一解，记

由(3)式，系统(1)可经变换

其中h(ξ)，g(ξ)，p(ξ，η) 在原点邻域解析，且h(0)=g(0)=0.

专著[1]在定理7.2和定理7.3中引述了专著[2]中对幂零奇点的有关研究结果，转述如下:

定理 1.1系统(1)奇点O(0，0)的性态由下式判定，其中当k=2m+1时，

在(5)式的最后一项中的“怪点”，在定理7.2引述的结论中说:这类奇点邻域由一个椭圆扇形和一个双曲扇形组成，如图2所示.

图1 k=2m时系统怪点的小邻域内的相图

图2 k=2m+1时系统退化奇点的小邻域内的相图

本文主要从以下三个方面进行阐述:幂零奇点小邻域内相轨线的拓扑结构，幂零奇点的中心问题，幂零奇点的局部分支问题.第二部分给出一些具体的例子说明在幂零奇点小邻域内相轨线可能存在不同的拓扑结构.第三部分对焦点量的计算方法进行总结，进而对中心与解析中心问题进行阐释.第四部分主要对幂零奇点小邻域内的极限环分支问题进行总结.

2 幂零奇点小邻域内相轨线的拓扑结构

图2有一个值得注意的特点，即所有过原点的相轨线都是原点邻域的奇闭轨线.然而，在本节中将举例说明，可能存在过这类奇点的开轨线，即这类奇点邻域相轨线的拓扑结构与图2可能有所不同.由定理1.1，系统(1)原点为“怪点”的充分必要条件是n为奇数，且下列条件之一成立:

兹举例说明当上述条件之一成立时系统(1)可能存在过原点的开轨线，其原点邻域相轨线的拓扑结构不同于图2.

例2.1考虑二次系统

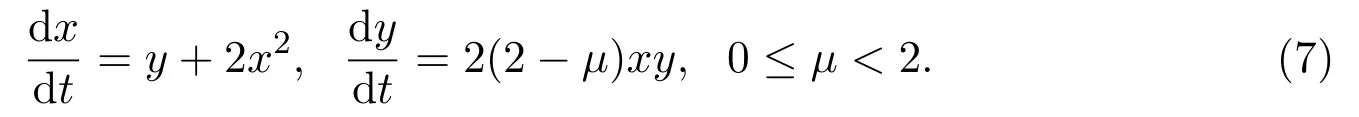
令ξ=x，η=y+2x2，系统 (7)化为

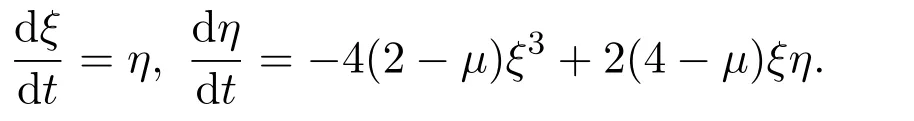
从而对系统 (7)而言，k=2m+1=3，m=n=1，a3=-4(2-μ)＜0，b1=2(4-μ)，，原点O(0，0)是系统 (7)的 “怪点”.

如果0，则系统 (7)的首次积分为.以下仅就μ=0与μ=1两种情况讨论系统(7)的相图.

当μ=0时，系统(7)化为

其右端函数满足(6)式中的条件C1.系统(8)的首次积分为

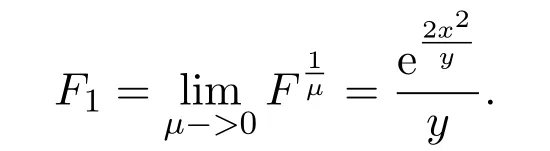
由此得到系统(8)的相图如图3(a)所示.由于系统(8)有一条过原点的直线解y=0，故从大范围看，图3(a)与图2的结构有所不同.

当μ=1时，系统(7)化为

其右端函数满足(6)式中的条件C2.系统(9)的首次积分为

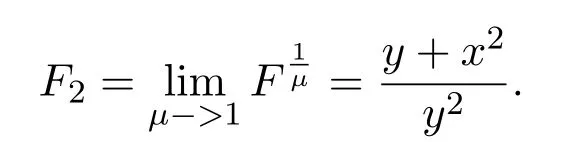
其相图如图3(b)所示，其结构与图3(a)有很大的不同，兹说明如下:

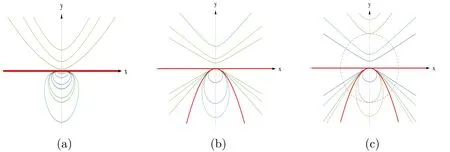
图3 系统(7)在不同参数下的相图

(1)直线Γ1:y=0与抛物线Γ2:y+x2=0都过原点，是系统(9)的两条特殊的代数曲线解，把相平面分割成下列四个子域:

(2)对任一固定的常数c＞0，曲线F=c是系统(9)的一条双曲线解，其一支位于上半平面D1，另一支位于下半平面以Γ1，Γ2为边界的区域中，且过原点;

(3)对任一固定的常数c＜0，曲线F=c是系统(9)的一条椭圆曲线解，位于下半平面以Γ2为边界的区域D3中，且过原点.

综上所述:对系统(9)而言，上半平面，D1是一个双曲扇形，是两个抛物扇形，而D3是一个椭圆扇形.

然而，如果只把目光局限在原点充分小的邻域，则图3(a)与图3(b)中相轨线的拓扑结构是一样的，在原点的小邻域内的结构都如图3(c)所示.

在整个Poincaré圆盘上，系统(8)与系统(9)的全局相图分别如图4与图5所示.其中图4含两个子域，图5含四个子域.

图4 系统(8)的全局相图

图5 系统(9)在不同参数下的全局相图

图2原点邻域相轨线的拓扑结构与图3(c)一样吗？

怪点邻域(小范围)以及与怪点有关的子域(大范围)相轨线究竟有哪几种拓扑结构？如何判断？

例2.2考虑三次系统

对系统 (10)作变换ξ=x，η=y+x2-x2y，得

从而对系统 (10)有k=2m+1=5，m=2，n=1＜m，a2m+1=-2＜0，bn=2，故 (6)式中的条件C3成立，原点是“怪点”.

系统(10)的首次积分为

其中抛物线y+x2=0与直线y=0是系统(10)的代数曲线解.

系统(10)原点邻域的相图类似于图b(参见图6).

图6 系统(10)的原点小邻域内的相图

3 幂零奇点的焦点量计算与中心问题

当奇点是幂零奇点且满足在(5)式的中心型奇点的条件时，一个重要的问题就是中心焦点的判定问题.而解决该问题的主要方法就是焦点量的计算.对于幂零奇点，由于其退化性，初等中心型奇点的焦点量的计算方法不再适用，本节主要对焦点量的计算方法进行总结.由定理1.1得

性质 3.1设函数y=f(x)是隐函数方程(2)在原点邻域的唯一解，则系统(1)原点为中心或焦点的充分必要条件是存在一个的正整数n，使得

当原点为幂零奇点时，专著[2]中通过变换

把系统(11)化为

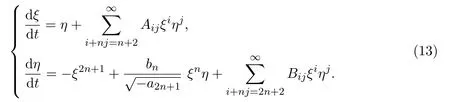
在理论上，诸νk(ϑ)可以逐项求出，故可定义焦点量，细焦点及其阶数等概念，并可研究后继函数的零点.从而可以把有关后继函数的理论作为研究系统(1)原点的中心焦点判定与极限环分支问题的最原始的理论根据.

然而，在针对具体系统进行研究时，要把诸νk(ϑ)逐项求出来是有困难的.

说明 3.1在变换 (12)中，若用f(x)代替fn+1(x)，则可使由系统 (1)得到系统(13)的推导较为简单.但由于f(x)通常不能精确地求出，故在针对具体系统进行计算时还得使用fn+1(x).

专著 [2]中还证明了:如果bn=0，则可逐项确定在原点邻域定正的形式级数F(x，y)，使得

由于避免了逐项积分，故{Vk}比{νk(2π)}容易计算.然而如果在{Vk}中第一个不为零Vk下标可能为奇数，故不能直接由它的正负符号来判定系统(1)原点的稳定性.

专著[2]以及文献[3-7]中研究了系统(1)原点邻域的规范型.由专著[2]中的定理19.10得

定理 3.1当性质3.1的条件成立时，存在形式变换

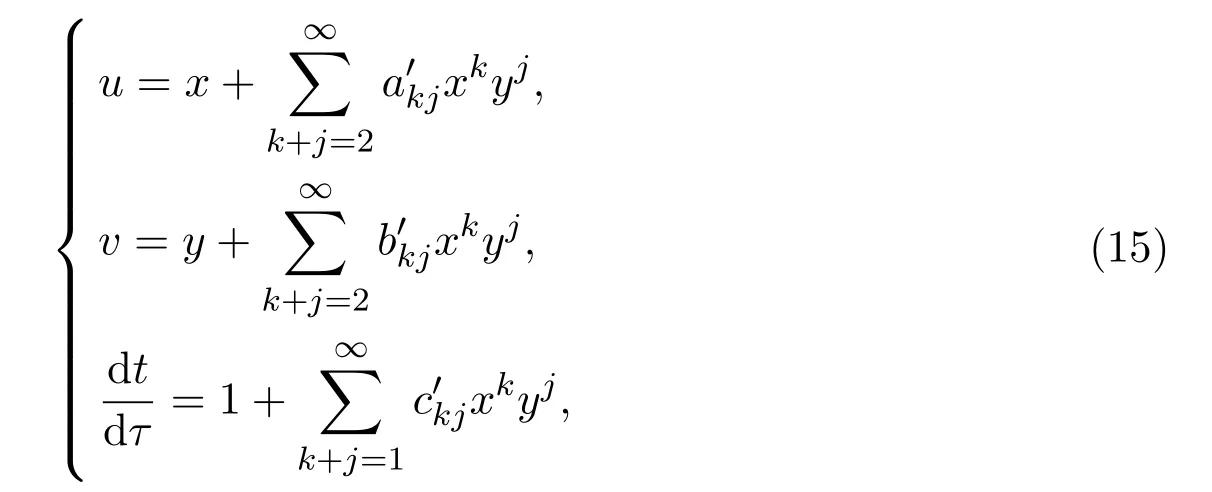
文献[7]中进一步证明了以下定理.

定理 3.2当性质3.1的条件成立时，存在一个形如变换(15)的在原点邻域解析的变换，使系统(1)经变换(15)化为下列Liénard方程

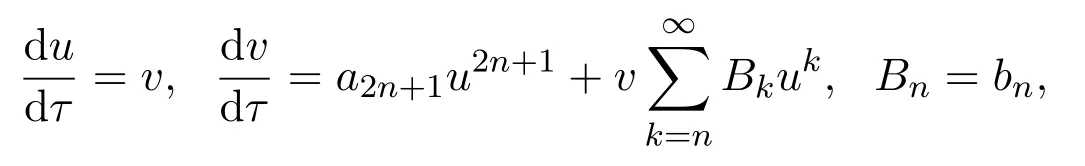
从而可以把诸B2k看作原点的各阶Lyapunov常数.

文献[8]对规范型的方法再次进行研究，给出相应的Maple程序.但是，无论广义极坐标变换还是规范型的方法，都牵扯到大量的符号计算，与初等中心的形式级数法，后继函数法相比较，其难度非常大.文献[9-10]专门研究了三次幂零奇点的中心焦点判定与极限环分支问题.

性质 3.2系统(1)的坐标原点为三次奇点，且为中心或焦点的充分必要条件是

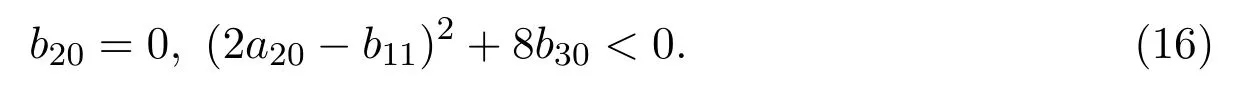
当 (16)式成立时，不妨设a20=μ，b20=0，b11=2μ，b30=-2，否则记

并对系统 (1)作变换ξ=λx，，从而可以把具有三次幂零型中心或焦点的实平面微分自治解析系统化为下列形式

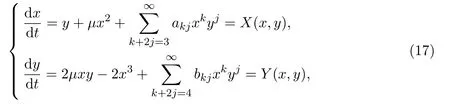
证明了该系统一定存在逆积分因子，并给出了计算焦点量的逆积分因子法，该方法只涉及系数的代数运算，计算较为简单.

说明 3.2逆积分因子法只适用于三重幂零奇点，对于更高重次的奇点，该方法不再适用.即使对于三重幂零奇点，当μ=0时，其计算量远小于0的情形.

对于幂零奇点，可积性条件并不意味着解析可积，也就是说中心不一定是解析中心，在原点的小邻域内不一定有解析的首次积分.例如系统

的原点是中心，但不是解析可积的.再例如对于系统

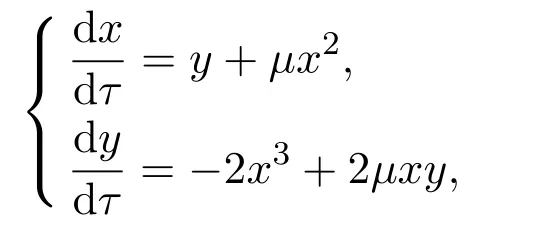
容易验证对于任何的μ，该原点都为中心，但是它也不是解析可积的.它在原点的小邻域内有如下首次积分.也就是说，对于幂零奇点，即使是中心，在奇点的小邻域内也不一定存在解析的首次积分，甚至连形式的首次积分也不存在.但是对于系统(17)，文献[11]运用逆积分因子法完全解决了具有三重幂零奇点的微分系统的解析可积问题.

说明 3.3对于具有三重幂零奇点的系统，μ=0是奇点解析可积的必要条件，这也能说明为何μ=0时其焦点量计算相对简单.

对于重次更高的幂零奇点的解析可积性，也就是解析中心问题，最近有很多学者给予了关注.文献[12-13]先后研究了下列系统

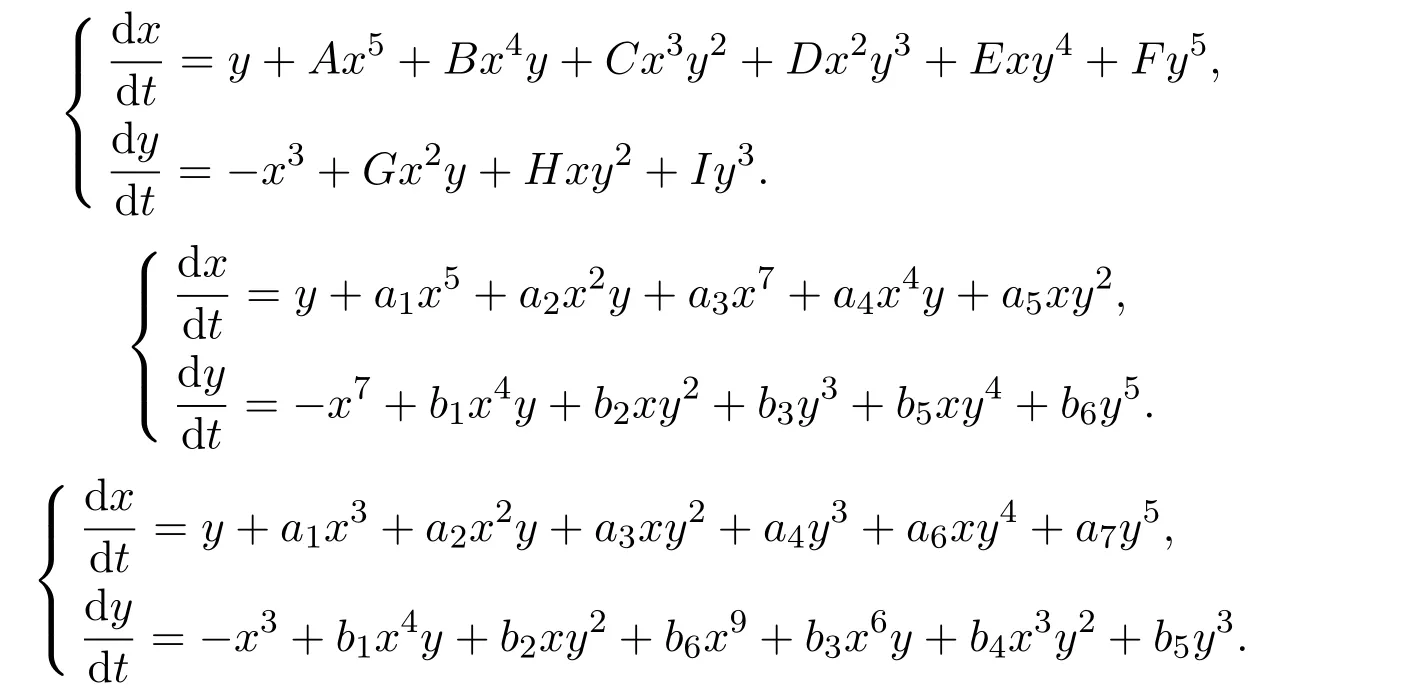
最近，对于退化程度更高的一些系统的解析可积性也有了一些较好的结果.文献[14-15]运用规范型的方法先后研究了下列三类系统

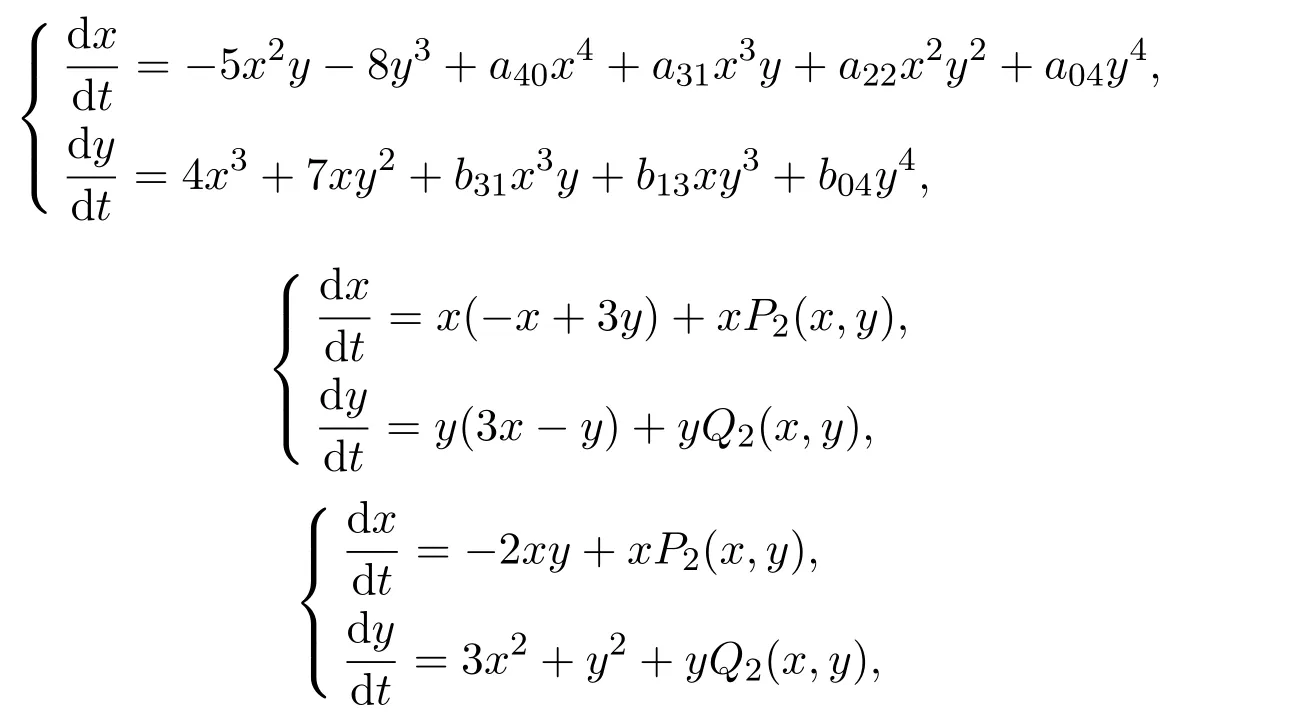
其中P2(x，y)，Q2(x，y)是齐二次函数，得到了原点解析可积的条件.随着退化程度的提高，奇点的可积性与解析可积性问题的难度也随之不断增大.

4 幂零奇点小邻域内的极限环分支问题

文献[6-7]证明了当系统(1)的原点为m阶细焦点时可以在原点邻域扰动出m-1个极限环.由于对系统的线性项没加扰动，故扰动系统的坐标原点仍为2n-1次高次奇点(即该奇点可以通过适当的扰动在原点邻域分解为2n-1个复初等奇点).对于系统

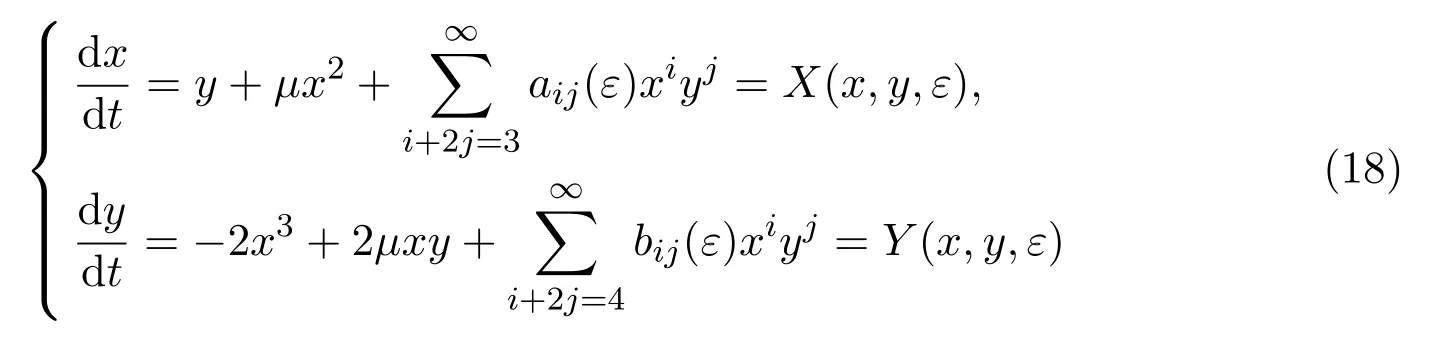
有如下定理.

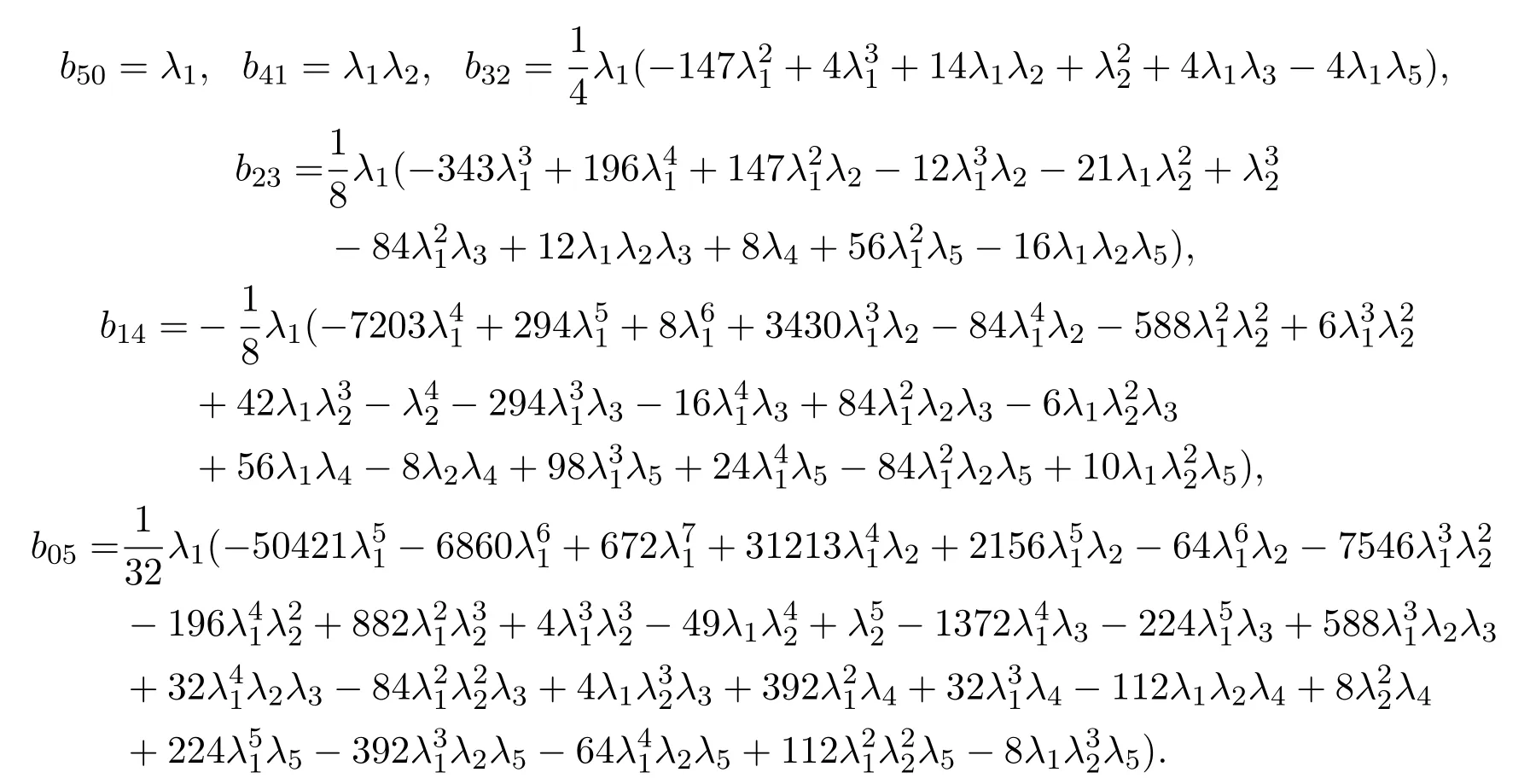
在退化奇点的小邻域内，其稳定性变得更加脆弱，动力学行为变得更加复杂，会出现更加复杂的分支现象，这都有待进一步的研究.