Duffing方程周期解的精确个数及其稳定性

陈红斌，邢慧，殷子健

(1.西安交通大学数学与统计学院，陕西 西安 710049;2.西安工程大学数学系，陕西 西安 710048;3.西北农林科技大学数学系，陕西 咸阳 712100)

1 引言

考虑Duffing方程

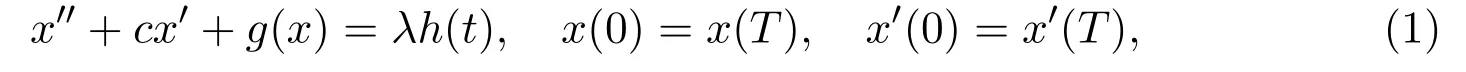
其中h是一个正的T-周期函数且g(x)是一个连续函数.方程(1)或者具有更为一般非线性项的二阶微分方程周期解的存在性和多解性已经被众多学者广泛研究.但是，关于方程(1)的周期解的确切个数的研究很少见.在文献[1]中，作者研究了小扰动问题，当h(t)充分小，在非线性满足简单的凹凸性条件时，得到了方程(1)恰有三个T周期解.R.Ortega在文献[2]中研究了下面带有参数的Duffing方程

其中c＞0且关于第二个变量是严格递增的，满足条件

得到的Ambrosetti-Prodi定理结果如下:

存在一个s0，使得当s＜s0时，方程(2)没有T周期解;当s=s0时，方程(2)有唯一稳定的T周期解;当s＞s0时，方程(2)恰有两个T周期解，其中一个是渐近稳定的，另一个是不稳定的.

以上结果是关于周期边值问题解的精确个数的首个完整的结果.关于周期解存在性的相关结果可参考文献[3-5].

在文献[6]中，J.Mawhin首先得到了关于一阶微分方程的类似结果.在文献[7]中作者利用奇点理论对该问题也进行了相关研究.在文献[8]中，A.Tineo利用Poincare映射的不动点定理对该问题也进行了研究.关于单摆方程的多解性的研究可参考文献[9-13]等.后来，在文献[14]中，作者研究了非线性项具有三次方即g(x)=ax-x3的情况，并假设非线性回复力g满足凹凸性条件，证明了方程(1)恰有3个T周期解.

在本文中，假定非线性回复力g有唯一的极小值点，采用分歧方法并结合极大值原理，得到了Ambrosetii-prodi定理，该结果减弱了文献[2]中的条件，对文献[2]中的结果有了本质的改进.本文的方法对于更为一般的非线性项g是适用的，可得到关于解的精确个数和稳定性的更为完整的信息.对于周期解的多解问题，可参考文献[15-17].关于周期解的稳定性和衰变速度可参考文献[14，18-22].

在本文中，如果g满足下面的条件

(i)g(x)≥0，g∈C1;

(ii)g(x)有唯一的非退化临界点x0使得g(x0)=0;

(iii)在x0的某个邻域内，g关于x满足g∈C2.

则称g是U-型的.即g是非负有唯一的零点x0，在x＜x0时是递减的，当x＞x0时是递增的，且g′′(x0)＞0.

在本文中，一律假设g(x)∈C1是U-型的且满足下面的条件

且h(t)＞0，h∈CT.

简而言之，本文的主要结果是当g具有U-型结构时，方程(1)的解曲线也是U-型的.确切的说，本文得到如下定理:

定理 1.1设g(x)∈C1是U-型的且满足条件(3)和.则

(i)当λ＜0时，方程(1)没有T周期解;

(ii)当λ=0时，方程(1)有唯一的平凡T周期解x(t)=x0;

(iii)当λ＞0时，方程(1)恰有两个有序T周期解，且其中较大的是稳定的，较小的是不稳定的.

如果g是U-型的，显然两个极限是存在的，或者其中一个是等于无穷的.当其中一个是有界时，例如，m-＜∞，假设以及则得到解曲线的性质如下:

定理 1.2设g(x)∈C1是U-型的，满足条件(3)且，m-是有界的，则

(i)当λ＜0时，方程(1)没有T周期解;

(ii)当λ=0时，方程(1)有唯一的平凡T周期解x(t)=x0;

(iii)当0＜λ＜λ0时，方程(1)恰有两个有序T周期解，且其中较大的是稳定的，较小的是不稳定的;

(iv)λ＞λ0时，方程(1)有唯一稳定的T周期解.

如果m±＜+∞，m-＜m+.设λ0=m-/，λ1=m+/.则上面的定理简化成下面的形式:

定理 1.3设g(x)∈C1是U-型的，满足条件(3)且m±＜+∞，m-＜m+，则

(i)当λ＜0时，方程(1)没有T周期解;

(ii)当λ=0时，方程(1)有唯一的平凡T周期解x(t)=x0;

(iii)当0＜λ＜λ0时，方程(1)恰有两个有序T周期解，且其中较大的是稳定的，较小的是不稳定的;

(iv)当λ0＜λ＜λ1时，方程(1)有唯一稳定的T周期解;

(v)当λ＞λ1时，方程(1)无T周期解.

下面是一些记号方便后面使用.

(1)当 1≤p≤∞时，表示T-周期函数u∈Lp[0，T]，范数记为‖u‖p;

(2)当k≥0，在Ck-范数下，表示T-周期函数u∈Ck[0，T];

(3)α(t)≫β(t)，表示α(t)≥β(t)且在正测度子集上α(t)＞β(t).

2 线性周期问题

本节回顾线性周期边值问题的基本结果以备后用.考虑周期边值问题

其中F:[0，T]×Rn→Rn是一个连续函数且当n=2时是关于t是T-周期的.

记x(t，x0)为初值问题(4)的解.

定义 2.1如果线性化方程

没有非平凡的T周期解，则方程(4)的T周期解被称为是非退化的.

设M(t)是方程(5)的基解矩阵，且μ1和μ2是矩阵M(T)的特征值.如果|μi|＜1，i=1，2，则x(t，x0)是渐近稳定的，否则，如果其中一个的模大于 1，则x(t，x0)是不稳定的.

考虑下面齐次周期方程

其中c＞0是一个常数且α(t)∈LT.

下面的引理在文献[1]中给出，在证明本文结果中起着重要的作用.

引理 2.1设α(t)∈LT使得

如果α(t)≪0或α(t)≫0时，则方程(6)的可能的T周期解x是平凡的.

下面是关于周期解的稳定性的结果，在文献[23]中已给出.

引理 2.2设x是方程(2)的一个孤立的T周期解使得条件成立，则

(i)如果α(t)≫0，则x是渐近稳定的;

(ii)如果α(t)≪0，则x是不稳定的.

考虑微分方程

其中c是一个常数且α(t)，h(t)∈LT.

为了得到带有满足凸性条件的非线性项g的Duffing方程解的精确个数，需要下面改进的极大值原理，这个极大值原理推广了文献[15]中由P.J.Torres和M.R.Zhang得到的定理2.3的结果.

引理 2.3设h(t)≫0且α(t)满足.如果x(t)是方程 (8)的一个T周期解，则下面的结论成立:

(i)对∀t∈R，则x(t)＞0或者x(t)＜0;

(ii)对∀t∈R，如果α(t)＞0，则x(t)＞0;

(iii)对∀t∈R，如果α(t)＜0，则x(t)＜0.

证明首先证明结论 (i).用反证法，如果x(t)在 [0，T]上变号，则存在一个τ使得x(τ)=0.假设x′(τ)≤0，否则，如果x′(τ)＞0，由于x(t) 是一个T-周期函数，x(t)在 [τ，τ+T)有一个连续的零点t0，使得x′(t0)≤0.在这种情况下，设τ=t0，不失一般性，假设τ=0使得x′(0)≤0.设v(t)是下面方程

初值问题的解，使得v(0)=v′(0)-1=0.由假设可得方程 (9)在 [0，T]上是非共轭的，其中λ1是特征问题y′′-cy′+λx=0，x(0)=x(T)=0 的第一特征值.从而可得对∀t∈(0，T]有v(t)＞0.方程 (8)乘以v(t)，方程 (9)乘以x(t)，两式作差并在[0，T]上利用分部积分得

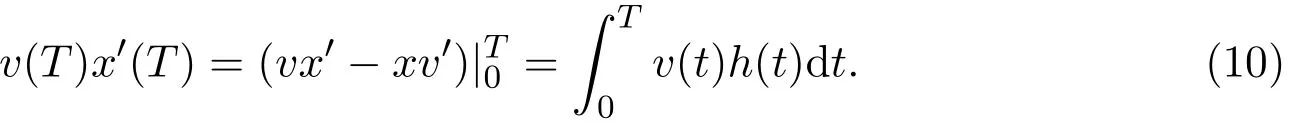
上式等号左边是负的，而右边是正的，矛盾，因此对∀t∈R，则x(t)＞0或者x(t)＜0.对方程(8)在[0，T]上积分易得当α(t)＞0时，有x(t)＞0，当α(t)＜0时，有x(t)＜0.结论(ii)和(iii)得证.

3 定理的证明

本节首先给出定理1.1的证明，以下引理对证明定理十分关键.证明中主要采用了连续延拓的方法.在给出证明前，首先回顾 Crandall-Rabinowitz分歧定理.具体细节可参考文献 [24]由 H.Kielhöfer编写的第一章 1.4节的内容或参考文献 [25].设F:U×R→Z，开集U⊂X，其中X和Z是 Banach空间.下面首先给出Crandall-Rabinowitz分歧定理:

引理3.1设F:U×R→Z在U×V⊂X×R上是连续可微的且满足下面3个条件:

(i)对某个 (x0，λ0)∈U×V，有F(x0，λ0)=0 且 dimN(DxF(x0，λ0))=1;

(ii)DxF(x0，λ0)) 的 Fredholm 指标是 0;且 codimR(DxF(x0，λ0))=1;

(iii)DλF(x0，λ0)(DxF(x0，λ0)).

则存在一条连续可微的曲线通过(x0，λ0);也就是说，存在

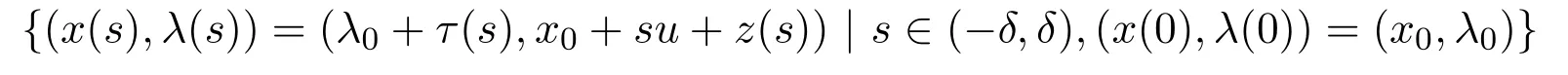
使得F(x(s)，λ(s))=0，∀s∈(-δ，δ)，并且在 (x0，λ0) 的邻域内，F(x，λ)=0 的所有解都属于这条曲线，其中Fλ((x0，λ0))的核空间为由u生成的子空间，且

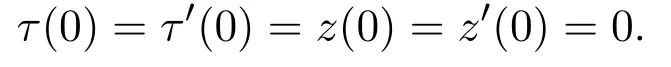
下面证明本文的主要结果，首先证明定理1.1.

证明当λ＜0时，如果方程 (1)有一个T周期解x(t)，则在区间 [0，T]上对方程(1)进行积分得

由于h(t)是正的，从而得等式的右边是负的，而等式的左边是正的，矛盾，所以定理1.1的结论(1)得证.当λ=0时，下面证明方程(1)有唯一的T周期解x0.在这种情况下，方程(1)化为

设x(t)是方程(11)的任意T周期解.方程(11)乘以x′(t)，并在区间[0，T]上积分可得

由上式可得x(t)是常数，将x(t)=c代入方程(11)可得g(c)=0.由函数g的假设条件得x(t)=c=x0.从而定理1.1的结论(2)得证.

当λ＞0时，采用分歧的方法进行证明.下面分为三步进行证明.

第一步:首先，证明 (x，λ)=(x0，0)是一个分歧点.设，Z=CT，且F(x，λ)=x′′+cx′+g(x)-λh(t)，显然F:X×R→Z是一个非线性 Fredholm 算子且F(x0，0)=0.为了证明(x，λ)=(x0，0)是一个拐点，下面验证引理 3.1的条件.F在点 (x，λ)=(x0，0) 的 Frechet 导数如下:Fx(x0，0)v=v′′+cv′+g′(x0)v=v′′+cv′.考虑线性方程

显然，方程(12)有唯一的常数T周期解.由此可得N(DxF(x0，0))=span[1]，即线性算子DxF(x0，0))的核空间是一维的.下面验证 codimDxF(x0，0)=1.考虑自伴算子，方程(12)的共轭方程如下:

显然自伴算子的核空间N(DxF*(x0，0))=span[1].由Fredholm二择一定理可得

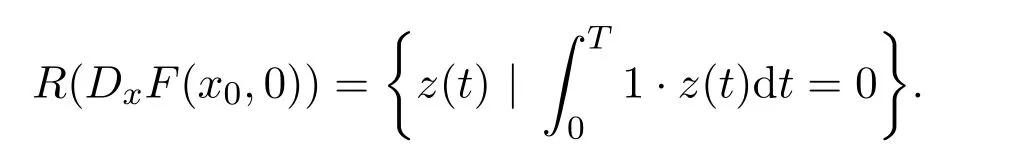
由于DλF(x0，0)=-h(t)和，从而证明了DλF(x0，0)(DxF(x0，0)).

根据引理3.1可得，存在连续可微的曲线通过(x0，λ0)，也就是说，存在

使得F(x(s)，λ(s))=0，s∈(-δ，δ)，并且在 (x0，0) 的邻域内，F(x，λ)=0 的所有解都在这条曲线上.

对方程(1)，关于s求二阶导数并在(x0，0)处取值得

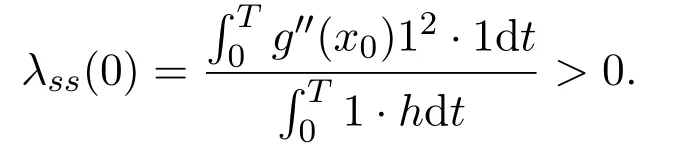
因此，(x，λ)=(x0，0)是F(x，λ)=0 的分歧点.

根据引理 3.1即 Crandall-Rabinowitz分歧定理可得，当λ＞0时，在 (x0，0)的某个邻域内，存在两个解分支x±(t，λ) 通过 (x，λ)=(x0，0) 且有x-(t，λ)＜x+(t，λ).更进一步，当λ＞0 时，有x-(t，λ)＜x0＜x+(t，λ).显然，x0满足

则方程 (1)与方程 (15)作差，令u=x(t)-x0，可得如下方程u′′+cu′+p(t)u=λh(t)，其中p(t)=(g(x(t))-g(x0))/(x(t)-x0)满足条件(3).由此可得，u＞0或u＜0，证得以上结果.

第二步:现在已经证得方程(1)有确切的两个T周期解，下面采用连续延拓的方法证明对∀λ＞0，方程 (1)有两个解.首先，证明当λ＞0时，x+(t，λ)关于λ＞0是递增的.

考虑在x(t)=x+(t，λ)处的线性方程

由于x(t)=x+(t，λ)＞x0且g′(x)＞0，由此可得 0＜g′(x(t))且满足条件 (3)，根据引理 2.1结论 (3)得上述方程没有任何非平凡解，也就是说，x(t)=x+(t，λ)是非退化解.因此x(t)=x+(t，λ)有关于λ的连续导数.对方程(1)关于λ求二阶导数得

由反极值原理得xλ＞0，从而证得x+(t，λ)关于λ是递增的，随着λ的递增，不仅x+(t，λ)是存在的，而且是非退化的.因此，对∀λ＞0，解曲线x+(t，λ)是存在的.类似可得，对∀λ＞0，x-(t，λ)也是存在的.

第三步:对固定的λ，设x(t)是方程 (1)的任意解.下面证明x(t)≡x+(t，λ)或x(t)≡x-(t，λ).首先，用类似第一步的证明方法容易验证x(t)＞x0或者x(t)＜x0.不妨设x(t)＞x0，则u=x(t)-x+(t，λ) 是下面方程u′′+cu′+p(t)u=0 的解，其中p(t)=(g(x(t))-x+(t，λ))/(x(t)-x+(t，λ)).显然，0＜p(t) 且满足条件 (H)，由引理 2.1可得u≡0.类似地，如果x(t)＜x0时，则x(t)≡x-(t，λ).由引理 2.2易得每个解的稳定性.定理1.1证毕.

注 3.1由于定理1.2和定理1.3的证明思想和定理1.1类似，所不同的是需要采用L-S约化方法处理解的存在性，这里就不再证明.