以企业自然天赋为基础而重建的生产者理论

林益

(宾夕法尼亚州立高等教育系统滑岩分校，美国 宾夕法尼亚滑岩 16057)

1 引言

在经济决策研究中，一种常用的方法是首先引入一个目标函数，如效用函数，生产函数，利润函数等，然后基于某种成本收益分析，决策者对这个目标函数进行优化[1-2].然而，正如行为经济学家所批评的那样，尽管这种方法已经被伪造的经验证据反复证实[3]，它并没有捕捉到现实生活的场景[4-5].因此，在公司这个微观层面上，在经济决策研究的最根本层面上，下面的问题自然会出现:在进行生产决策时，每个公司真的会经历这样一个一般的决策程序吗？

从理论上讲，上面所述的经济决策研究中常用的方法被广泛称为理性假设.以理性(rationality)为名的大量相关文献充分证明了这个问题的重要性.尽管这个理性假设仅仅在最近几十年才受到行为经济学家的批评，但是许多学者早已广泛感受到，并且一直在探索这个假设所隐含的内在意义及不确定性[6].这些学者包括Gary Becker[7]，Frank Lovett[8]，Fritz Machlup[9]，Ariel Rubinstein[10]，Paul Samuelson[11]，Herbert Simon[12]，LL Thurstone[13]，Max Weber[14]和 Glen Weyl[15].综上所述，在使用这种方法数十年之后，学者们仍在讨论理性假设的真正含义[6].这一现象间接解释了为什么最近的事件，特别是2008年开始的金融危机，迫切地提出了需要重建经济以及各种商学理论.例如，考虑到现有的经济，商学理论无法及时描述，预测和解释近期的金融风暴，Paul Krugman在《纽约时报》(2009-09-02)上发表如下评论:

经济学界已经误入歧途，因为经济学家作为一个群体误将优雅，数学的美丽认为是真理······随着对大萧条的记忆的消退，经济学家重新爱上了旧的，理想化的经济愿景，在那里理性的个体在完美市场中互动······不幸的是，这种浪漫化，净化过的经济愿景导致大多数经济学家忽略了······可能出错的情况.他们对人类理性的局限性视而不见，而这个局限性往往会导致泡沫和泡沫的破裂;导致机构失控的问题;导致市场的不完善······所有这些可能导致经济体······经历突然的，不可预测的崩溃;导致由于监管机构不相信监管所带来的危险.

与此同时，Paul De Grauwe在《金融时报》(2009-07-21)上写道:主流(经济)模型认为，经济个体非常了解世界的深层复杂性······他们有 “理性预期”······他们都理解相同的“真相”，他们都以相同的方式行事.因此，只需对一个代理(“具有代表性的”消费者和“具有代表性的”生产者)的行为进行建模，就可以充分描述世界的复杂性.很少有如此多的学者认可并认真地对待如此荒谬的想法.

从实际应用的角度来讲，之前所提出的问题的重要性体现在，未能预测迫在眉睫的经济危机的发生，例如始于2008年的大衰退，以及过去几十年速度相对缓慢的，作为新经济大国中国的崛起.具体地说，对于开始于2008年的大衰退，经济学家根本没有预见到危机正在酝酿之中;也没有预测到房价泡沫破灭时会有令人惊讶的破坏性后果[16].相比之下，许多学者对衰退背后的原因提供了不一致的，事后诸葛亮式的各种解读[17-18].至于中国的崛起，西方的学者和商界领袖肯定是一再对形势做出极大的误判.按时间顺序，相关事件发生如下:

·1992年，《时代》杂志自信地断言[19]:“中国不可能在21世纪成长为工业巨头.它的人口太多，国内生产总值太小.”

·1999年，(美国)科学院国家研究委员会[20]认为，与美国独特的创造新知识并将这些知识转化为服务，造福所有人的系统相比，中国在21世纪几乎不重要.

·2014年，与许多其他人一样，Abrami及同事[21]声称:“中国在很大程度上是一个死记硬背的国家，他们只能模仿，不能创新”，同时信息技术的进步只能由自由的思想家在自由社会中取得，而不是在防火墙后面的专制政权下.

·2020年，使谷歌成为世界领先科技公司的Eric Schmidt指出:“美国现在正在面临一个经济和军事竞争对手—中国，该竞争对手正积极地试图缩小我们在新兴技术方面的领先地位[22]”.“除非这些趋势发生变化，否则到21世纪30年代，将与一个拥有更大经济，更多研发投资，更高质量研究，更广泛部署新技术和更强大计算基础设施的国家竞争[23]”.

·2021年，Allison及同事[24]考察了过去20年中美在每项关键技术上取得的进展.他们发现中国已取代美国成为世界顶级高科技制造商，成为21世纪基础技术中的重要竞争对手;在某些项目的竞争中，中国已经成为第一;而在其他项目的竞争中，中国在未来十年内将超过美国.

综上所述，无论是经济理论的发展和应用，还是相关的商业研究，都需要重新建立相关理论，从而使得出的结论比以前更接近真实.为了解决上面所述的具有根本性的重要问题，作为朝着这一目标迈出的第一步，本文的全部推理和分析都是基于企业的四种自然天赋:自我意识，想象力，良心和自由意志.这样非常规地操作，使得这项研究有能力重新审视当今流行的生产者理论中一些最著名的结果.同时，这项研究论述了在什么条件下一些已知的结论才可以成立.其中，生产者理论正是一种迫切需要重新建立的经济理论之一.

本文的其余部分安排如下.第2节为以下各节的分析和讨论的顺利进行做必要的准备.第3节着眼于推广著名的Hotelling引理.第4节类似地探讨了Shepard引理的推广.第5节研究了为什么社会大范围的偏好顺序不可能现实地存在.第6节结束本文的讨论，并且提出了一些重要的，可供未来研究的未解决问题.

2 准备工作

本节从三个不同的角度介绍这项工作所需要的准备知识.首先，指出存在于科学革命以来微积分的发展与当前大数据时代之间的平行关系.其次，引用文献中有关公司的自然天赋及其在公司决策中所起作用的相关结论.第三，列出下面讨论所需的约定和必要的符号术语.

2.1 微积分发展与当今大数据时代的并行线

跨越16-17世纪在欧洲发生的科学革命导致了现代科学的出现[25].在此期间，随着物理学，天文学和生物学的一些重大发展，数学也进入了一个崭新时代.在历史上，这个数学新时代拥有许多的亮点[26-27]:

·John Napier发明的对数.

·Thomas Harriot和William Oughtred为代数所引入的概念和符号.

·Galileo Galilei所奠定的动力学科学.

·Johann Kepler通告的行星运动规律.

·Gerard Desargues和Blaise Pascal创造的纯几何.

·Rene Descartes推出的现代解析几何.

·Pierre de Fermat的现代数论基础.

·Christiaan Huygens对概率论的贡献.

·Isaac Newton and Gottfried Wilhelm Leibniz创立的微积分.

与本文相关，且值得注意的是以下相关内容 (更多相关细节，参见文献 [28，第 6章]):

(1)正是由Rene Descartes引入的笛卡尔坐标系帮助将几何和代数合并为一个有机整体，使现代解析几何的研究成为可能，同时为微积分的创造奠定了直观背景.

(2)尽管许多数据分析方法自几个世纪前就已出现[29]，但大量天文数据帮助Kepler发现了行星运动定律.通过运用这些定律，Kepler成功地使太阳系哥白尼模型中的圆形轨道[30]更加准确.换言之，尽管Kepler的发现本质上是经验性的，但是他为人们目前对太阳系的认知奠定了基础.由于Kepler使用的数据仅限于太阳系，他无法得出关于遥远恒星的一般理论.相反，他仍将这些遥远的恒星视为薄而固定的天体球面中的物体.

(3)Isaac Newton在其开创性的《原理》中阐述了运动定律和万有引力定律.利用这些定律，Newton不仅在理论上推演出了Kepler行星运动定律，从此将经验猜想转化为理论定理，而且还成功地完成了一个超越了太阳系的，新宇宙学的提炼.

如果将Newton和Leibniz时代以来微积分的发展与当前的大数据时代进行比较，就可以发现两条明显的平行线:(i)在大量行星运动的天文数据基础上，发现了在太阳系中成立，有效的经验规则;(ii)在最近收集的大量的大数据中，观察到越来越多的有关数据来源处的经验规则.特别是，根据(i)所指引的路径，微积分的发展使得科学界能够以分析的方法得出许多理论性的结果.这些结果不仅适用于太阳系及更远的宇宙，而且帮助提供了一种历史上从来没有的，全新的方法论方法;为现代科学的发展奠定了基础.因此，根据(i)和(ii)的平行性，能够大胆地推测出接下来的情况和可能发生的事情:人类目前生活在一个知识的黄金时代;在这个时代中另一种全新的方法论将会出现;在这个方法的基础上，科学将迎来另一个大发展的新纪元.

随着人类处理海量大数据能力的不断提高，新方法论将帮助人们首先在理论上确认所发现的经验公式是否正确，然后帮助人们得出经验手段无法得到的一系列理论结果.为此，自然有人会问，为什么现在的科学与技术不能很好处理大数据.要回答这个问题，需要首先意识到，现在的，最近才为公众所知的大数据时代，实际上在几十年前已经出现了.几十年前，当大量而多维的气象数据被采集的时侯，人们现在所知的大数据时代就已经出现了.在对灾害性天气状况进行及时预报的各种顽强尝试中，虽然运用了各种科学理论和现代技术，但是除了提高了现场直播，报道的精度之外，并没有取得多少明显的成功[31].因此，勤奋并且锲而不舍的气象学家们所缺乏的成功间接表明，现在这个时代需要一种与现代科学和现代数学完全不同的新方法论及方法来处理海量的大数据.由此来确认基于大数据的经验公式与结论，并推导出有关经济个体行为的理论.值得注意的是，人类行为比自然灾害更难预测.前者通常会随着预测而调整，而后者的自然进程不会根据预测到了的结论而改变.

2.2 企业的自然天赋和决策

为了开发所需的方法，注意到:尽管随着时间的推移，不同名称的更抽象的概念与对象被逐渐引入，但是本质上说来，现代科学和数学的大部分都是基于数的概念发展而来的[27].在数的概念被抽象的同时，数字背后的系统结构被有意识地忽略了[32].例如，数字1的概念是从1个苹果，1张桌子，1个椅子等现象中抽象出来的.当从这些情况中抽象出数字1时，苹果，桌子，椅子等的内部系统结构就被忽略了.然而，就经济，商业研究而言，所得到的理论主要是关于商业个体如何发展，演变以及它如何与其他的商业体互动.也就是说，商业理论强调的是被经济研究中广泛采用的方法所通常忽略的系统结构与演化[33].为了克服这一重要的方法论上的缺陷，在使生产者理论更适合现实的努力过程中，将每家公司(企业)视为一个有生命的存在，以便其每一个决策都是基于其独特的价值观和信仰体系.而这样的体系存在于企业的自然天赋之上，并由企业的自然天赋所决定.

与个人的四种自然天赋 — 自我意识，想象力，良心和自由意志[34]相平行地，Forrest，Hafezalkotob等人[35]为公司创立了一套相应的自然天赋.具体来说，一个企业的自我意识是指该企业意识到自己作为一个商业实体的存在，自己是独立于其他实体的.这里的其他实体可以是人，公司或者事物.自我意识使得企业认识到，其自身拥有属于自己的商业秘密，如所采用的营销手段，运营策略，受保护产品设计等.一个企业的想象力描述了这个企业学习和获取新知识的能力.它帮助该企业以创新的方式，正确地想象什么是市场所需要的产品，包括新设计的产品，改进的产品或者新的(或改进的)服务.由此来满足该企业所认知的市场需求，并且制定出必要的生产过程来实现想象中的产品.一个企业的所谓的良心代表该企业判断哪种商业努力比其它的努力更具有价值的能力.一个企业的自由意志指的是，该企业能够遵守与各种商业伙伴签订合同中的承诺的能力.

通过使用系统思维和逻辑推理，Forrest和Shao等人[36]在试图找到理性假设的真正含义时[1-2，6]，推导出了下面的结果:

·每家公司努力的目标是至少部分地实现公司明确声明的使命.

·在宏观企业层面上，一个企业的理性假设代表在所有备选方案中找到最优选择，其中最优的标准由该企业的管理层根据企业的自然天赋来确定.

·每家企业(公司)都有其独特而唯一的价值观和信仰体系.

·当一家公司(企业)面临决策情况的时侯，它通过使用与其价值观和信念系统一致的，特定的最优标准在给定约束内，优化潜在对象.

例2.1为了帮助确认这些系统性结论的重要性，再来看一下Hu[37]和Lin[32，P136]所构造的一个特别的决策情况.假设某个公司的生产流程可以抽象为图1中的有向加权网络.该公司需要找到由生产节点X到生产节点Z的最小路径.

图1 不同的价值信念系统定义不同的最小解

情形1:该公司按照实数的常规排序方式对实数权重进行排序.在这种情况下，X→X1→Y→Z1→Z是该公司寻找的路径.该路径的权重为1.从节点X到节点Z的其他路径的权重分别为2，3和4.

情形 2:该公司参照 mod 4函数对实数权重进行排序.具体地说，对于任意两个实数x和y，x＜y当且仅当x(mod 4)＜y(mod 4).在这样一个决策系统中，X→X2→Y→Z2→Z是该公司所寻找的路径.这个路径的权重等于

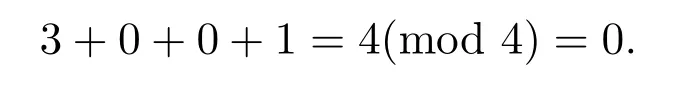
相比之下，其他路径的权重分别为1，2或3.证毕.

这个例子表明，不同的最优值的标准赋予不同的优化方法，导致不同的最优决策解.所有这些差异都源于各个公司不同的价值观和信仰体系.也就是说，尽管不同的公司可能着眼于相同的目标函数，但具体采用的最优值的标准或方法极有可能会因公司不同而不同.

基于上述讨论，假设每家公司都有一种特定的，由其价值观和信念系统所定义的方式，对属于其决策活动域D内的实数进行排序.假设公司的实数排序关系用≤F表示小于或等于，≥F表示大于或等于，=F表示相等.不失一般性，假设该序关系对D中所有实数进行排序并满足:(i)传递性:对于任意x，y，z∈D，x≤Fy和y≤Fz蕴含x≤Fz;(ii)自反性:对于任意x∈D，x≤Fx;(iii)反对称性:对于任何不同的x，y∈D，x≤Fy和y≤Fx不能够同时成立.

2.3 公司营运

本小节和本文的其余部分考虑一个随机选择的公司，将其称为公司或企业.当它以单位价格(或简称为价格)px购买数量x的某个商品时，该公司为其账户创建了数量为xpx的债务.相反地，当该公司以单位价格或价格py出售数量为y的某个商品时，它会在其账户中创建量为ypy的信用.

公司从其他经济体那里购买的所有商品(称为公司的输入)的数量，以及提供给市场的商品(称为公司的产出)数量，可以写成一个向量.为了在这个向量中将输入与输出分开，将输入商品的数量用负数表示，因为它们为公司制造了债务;将产出商品的数量用正数表示，因为它们象征公司的收入.假设所有商品都可以在市场上进行交易.同时假设市场上总共有ℓ种，排了序的商品;它们按照排序分别被标为 1，2，···，ℓ.正如经济分析中通常所做的那样[38]，为了使下面的分析得以进行，假设每种商品的需求，供给数量，无论是作为输入还是作为输出提供给市场，都是一个实数.

如果c=(c1，c2，···，cℓ) 代表公司所需的所有商品的数量向量，p=(p1，p2，···，pℓ)代表相应的商品的价格体系，那么公司账户的总现金流等于，其中·表示向量p和c的点积.不失一般性，假设每个价格系统p=(p1，p2，···，pℓ)仅包含正分量.也就是说，要获得任何商品，公司都必须付出代价.并且，对于商品向量c，它的大部分分量应该为零.这表示这些商品既不是公司的输入，也不是公司的产出.

至于商品，尽管它们是在当前时刻进行交换，仍然考虑交付的具体时间，以及买卖双方的交易地点.就如在现实生活中一样，把时间轴分成等长的，用自然数1，2，···标记的区间.按时间顺序，第一个区间从原点0开始，该点视为当前时刻.假设一个区间内的所有时刻都是不可区分的.同样，划分地域为有限的一些区域;商品在每个区域中进行交易.因此，当一种商品具有不同的交易时间，不同的交易地点时，这种商品将被视为具有指定时间和地点的不同商品.相应地，一个商品的价格是消费者现在需要为一个单位的这个商品所支付的金额.而为了简化下面的分析，将省略一切金钱的利息和折扣.此外，将忽略不同地点的金钱价值.也就是说，这篇文章不涉及货币兑换问题.

对于公司而言，其行动计划是确定其消费以及提供给市场的每种商品的数量.也就是说，它的行动计划 (或简称为行动)y=(y1，y2，···，yℓ)是从ℓ维欧几里得空间 Rℓ中选择一个元素;这个元素表示该公司消费及提供的商品数量，其中 R代表所有实数的集合;下脚标 1，2，···，ℓ表示所有的，可交换的各个商品.所以，动作y的价格由给出，其中p=(p1，p2，···，pℓ) 是所有商品的价格体系，yh代表商品h(=1，2，···，ℓ)的所需数量.如果y的第h分量为 0，则意味着该公司既不消费也不生产商品h.

在其约束范围内，公司选择最适合其特定价值观和信仰体系的行动计划.其中，如文献中广泛研究的那样，利润最大化仅代表一种特定的价值观和信念体系所要求的情景.设Y为公司所有可行生产计划的集合.也就是说，每个y∈Y都是公司的一种可能的，在技术上可实现的，并且符合公司价值观和信仰体系的道德规范的生产计划.

3 Hotelling引理的推广

其中p∈Rℓ代表商品的价格体系.在本文的其余部分，当表达式πF(p)出现时，除非另有说明，否则均假设上述最大值存在.

定理 3.1企业的利润函数πF是定义在上的部分函数.如果公司的价值观和信念系统与实数的常规排序一致，则πF在其定义域上是一阶齐次的.但是，通常情况下，πF不是一阶齐次的.

证明第一个结论来自以下事实:对于每个价格系统，不能保证

一定存在.至于第二个结论，对于任何标量λ＞0和任何p∈domain(πF)，

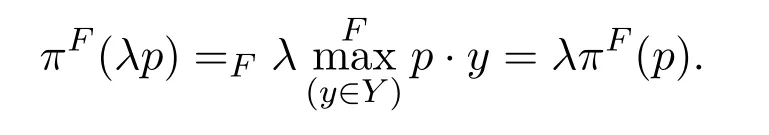
至于第三个结论，只需要构建一个反例来证实这个陈述.为了达到这个目的，稍微修改一下例2.1.为此，需借用Forrest，Hafezalkotob等人[35]从整数域推广到所有实数集的模函数(或简称为mod函数).特别地，a∈R为正数.在R上定义一个线性序关系＜mod(a)如下:对于任何x，y∈R，

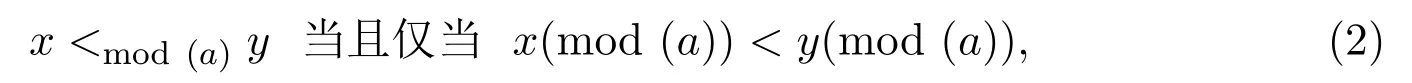
其中序关系＜是定义在R上定义的常规排序，x(mod(a))是x÷a的余数，y(mod(a))是y÷a的余数，满足0≤x(mod(a))＜a和0≤y(mod(a))＜a.当所有涉及的数字a，x，y都是整数时，这个序关系＜mod(a)退化为数论中广泛研究的那种序关系[39].换句话说，对于任何r∈R，满足0≤r＜a，以下实数集被分类为一个等价类.在不会引起混淆时，仍然用r表示这个等价类:

其中 Z 代表所有整数的集合，即 Z={···，-3，-2，-1，0，+1，+2，+3，···}.

十二小时制，每周7天，不同天数的月份，分别代表了模运算在现实生活中的一些常见用途.

例 3.1假设公司的某个特定生产线涉及一个单位的原料X，X1，X2，Y，Z1，Z2，Z的投入.其中X1和X2彼此可以相互替代，Z1和Z2也可以.图2中箭头表示这些原料一个接一个地输入生产线的顺序，而权重则表示生产顺序从一个节点到下一个节点所创造的相关利润.现在，生产部经理想要得到最大可能的总利润.

图2 具有各自利润空间的特定生产线

情况1:公司按照实数的常规排序方式对实数权重进行排序.在这种情况下，四种可能的路径及其各自的总权重可以如下所示:

·X→X1→Y→Z1→Z;其权重为5.

·X→X1→Y→Z2→Z;其权重为6.

·X→X2→Y→Z1→Z;其权重为7.

·X→X2→Y→Z2→Z;其权重为8.

因此，最大总利润等于8.为了证明对于任何标量λ＞0，

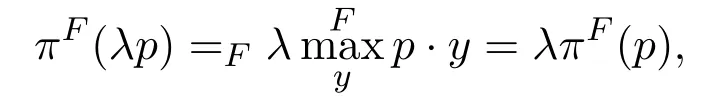
假设这里涉及的所有商品的排序如下:I={X，X1，X2，Y，Z1，Z2，Z}.让各自的路径分别如下标记:I1，1={X，X1，Y，Z1，Z}，I1，2={X，X1，Y，Z2，Z}，I2，1={X，X2，Y，Z1，Z}，I2，2={X，X2，Y，Z2，Z}.

因此相应的输入和相关的输出向量分别可以由下式给出:

现在，每个价格系统p可以写成，并且对于任何生产y，都有k(=1，···，4)使得当删除所有零分量时，有yin=(ky)，yout=(kZAC).因此，对于任何价格体系p和任何生产y，p·y=pin·yin+pout·yout，其中pin表示y中输入商品的子向量yin的价格子向量，pout表示在y中输出商品子向量yout的价格子向量.因此，对于任何标量λ＞0，有

情况2:公司参照mod 4函数对实数权重进行排序，使得对于任意两个实数x和y，x＜y当且仅当x(mod 4)＜y(mod 4).在这种情况下，上面列出的四种可能路径各自的总利润分别如下:5(mod 4)=1，6(mod 4)=2，7(mod 4)=3和 8(mod 4)=0.因此，最大总利润等于3.现在，设λ=3.2是乘以每个局部值的标量.四个路径对应的总利润分别等于

也就是说，有3.2×7(mod 4)/=3.2×6(mod 4).

至此定理3.1的例子和证明结束.

公司的最优生产札(optimal production correspondence)[40]是如下定义的部分集值函数:对于任何价格系统

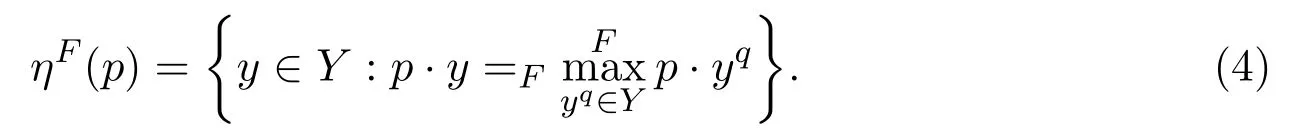
假设有一个生产y∈Y使得换句话说，ηF将每个价格系统p映射到所有利润最大化生产的子集ηF(p)⊂Y，如果该子集不为空.在本节的其余部分，假设公司的价值观和信念系统所暗示的实数的序关系与传统的序关系相同.

定理 3.2(广义 Hotelling 引理) 对于给定的价格系统p=(p1，p2，···，pℓ)∈Rℓ，如果公司的利润存在，则在p的某个邻域中η(p)为单一元素的集合，当且仅当π(·)相对于每个ph在p处是可微的，并且

对于任何y=(y1，y2，···，yℓ)∈η(p)，h=1，2，···，ℓ.

证明(⇒)因为在p的某个邻域中η(p)仅有一个元素，所以由包络定理(envelope theorem) 有: 对于y=(y1，y2，···，yℓ)∈η(p)，h=1，2，···，ℓ，(∂π(p))/(∂ph)=yh.

(⇐)对于任何，有

因此，等式(5)意味着

因此，y1=y2.也就是说，η(p)仅仅包含一个元素.证毕.

定义如下特征函数F:Y→R:

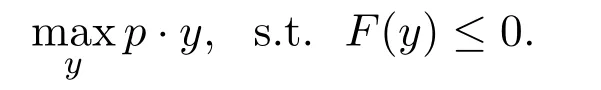
这个问题的拉格朗日量是

这意味着一阶条件

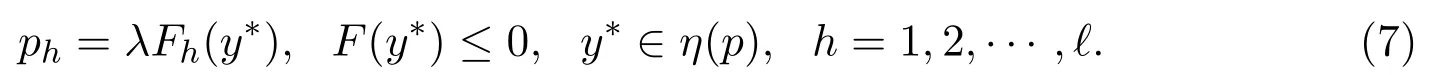
定理 3.3对于任何价格系统p=(p1，p2，···，pℓ)∈Rℓ，满足ph＞0，h=1，2，···，ℓ，如果y(p)∈η(p)是连续可微分的，则.

证明首先，计算Dpy(p)如下:

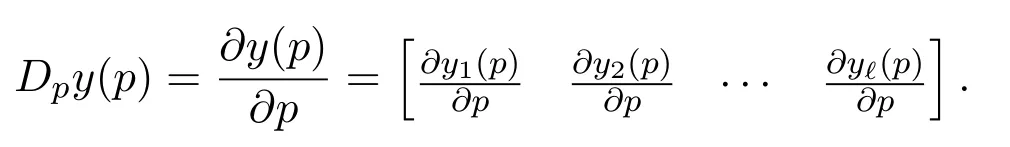
根据定理3.2，该式的右侧等于

如等式 (8) 中给出的，因为ph＞0，h=1，2，···，ℓ，矩阵Dpy(p)的一般 (t，h) 元素等于

所以，由等式(7)有

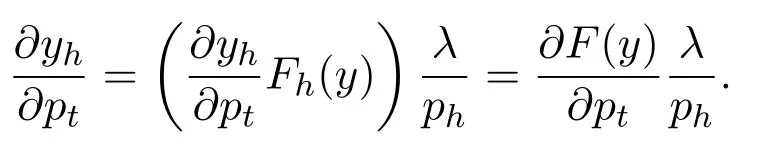
最后，由包络定理(envelope theorem)得到

定理3.3代表了生产者理论中一个著名定理的重大改进[40-41].具体的说，如果假设公司生产单一产品，并且η(p)仅仅包含一个元素，则矩阵被证明为是对称的，半正定的.与之相比，这里没有强加这些假设，并且得到更强的结论.

4 Shepard引理的推广

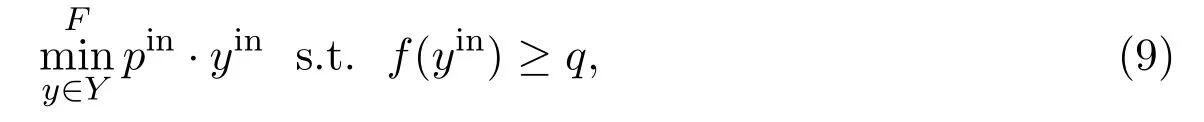
其中f(yin)=yout.假设表示出现在yout的分量中的所有商品下标集合的子集.不失一般性，假设这两个集合是相同的，因为生产超出q所列产品的额外产品至少需要增加劳动力投入.

令z=z(p，q)是等式 (9)中最小化问题的解.这个解称为一个条件要素需求[40]，因为它依赖于所需的生产产出q.如果令Z={z:∃y∈Y(z=yin，f(z)≥q)}，那么等式(9)中目标函数的最优值为

这个值给出了可以产生所需输出q的最小成本.因为任何非零生产计划的实施都必须使用一定数量的投入，如劳动力，工作空间等，并产生一定的产出，如废物，如果没有产生出任何有用的东西，所以有

称该函数为条件要素需求集合(即以期望的产出水平为条件).

根据方程(18)或包络定理，上式等于0.所以Dpz(p，q)=0t×t，这是因为无论p如何变化，z∈ξF(p，q)，F(z)=0.所以，F(z)对的导数为零.证毕.

定理4.3将生产者理论中的一个众所周知的结论进行了实质性的推广.特别是，生产者理论中的已知结果声称[40-41]矩阵是对称的，负半定的，并且满足Dpz(p，q).与之相比定理4.3的结论要强的多.

5 不存在任何社会层面的，统一的优先顺序

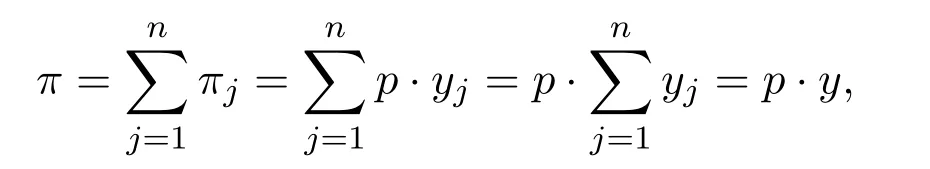
其中y称为总产量.在此设置中，每个生产者都被视为价格接受者，同时他们尝试通过选择最佳生产yj来最大程度地实现公司的使命.这其中最大值的定义和最大化方法均取决于生产者j的价值观和信念系统.考虑到每种价格和每种商品都与特定时间和地点相关，这种设置要求每个生产者选择其生产，以使其投入和产出在时间和空间上均得到最佳分布.这种最优生产称为生产者j相对于价格体系p的均衡生产(equilibrium production)[42].

假设≤j为生产者j在确定最优决策时采用的实数之间的序关系，并且≤为实数之间的常规序关系.对于有n个生产者的经济，定义实数集的序关系≤E如下，假设所讨论的经济体是处于一个民主的社会之中:对于任何a和b∈R，

这个等式(21)提供了亚当·斯密的隐形手存在的条件，对于更多细节请参见下面例5.1之后的讨论.然而，下面的范例表明，当允许某些公司的实数序关系不同于常规的实数序关系时，这个方程一般不成立.

例 5.1假设一个经济体有两个生产者，分别命名为1和2.他们的实数序关系均为≤mod(4).不失一般性，假设一个单位的每种相关商品要么是生产所需要的，要么是市场所需.

生产者1的具体生产情况如图3所示;它涉及一个单位的每种商品输入A，A?，B，C?，C，其中A?可以是A1或者是A2，但不能同时为两者;同样地，C?可以是C1或者是C2，但不能同时为两者.也就是说，商品A1和A2可以相互替代，商品C1和C2也是如此.在图3中，箭头表示相应商品一个接一个地进入生产线的顺序，而权重则表示生产顺序从一个节点到下一个节点所创造的相关利润.

图3 生产者1的生产线

将生产者1的各个生产线标记如下:

I11:A→A1→B→C1→C;

I12:A→A1→B→C2→C;

I21:A→A2→B→C1→C;

I22:A→A2→B→C2→C.

因此，生产者 1所有的可能生产线集合为Y1={I11，I12，I21，I22}，对应的利润分别为 1.345，1.36，6.085 mod(4)=2.085和 6.1 mod(4)=2.1.也就是说，有

对于生产者 2，其生产线如图 4所示;其涉及一个单位的每种商品输入U，U?，V，W?，W，其中U?可以是U1也可以是U2，但不能同时为两者.同样地，W?可以是W1也可以是W2，但不能同时为两者.也就是说，商品U1和U2可以相互替代，商品W1和W2也是如此.类似于上面的图3，在图4中，箭头代表相应商品依次送入生产线的顺序，而权重则代表生产顺序从一个节点到下一个节点所创造的相关利润.

图4 生产者2的生产线

将生产者2的各个生产线标记如下:

J11:U→U1→V→W1→W;

J12:U→U1→V→W2→W;

J21:U→U2→V→W1→W;

J22:U→U2→V→W2→W.

因此，生产者 2所有的可能生产线集合为Y1={J11，J12，J21，J22}，相应的利润分别为 6.1 mod(4)=2.1，4.135 mod(4)=0.135，3.31，1.315.也就是说，有

因此，根据等式 (22)和等式(23)，得到

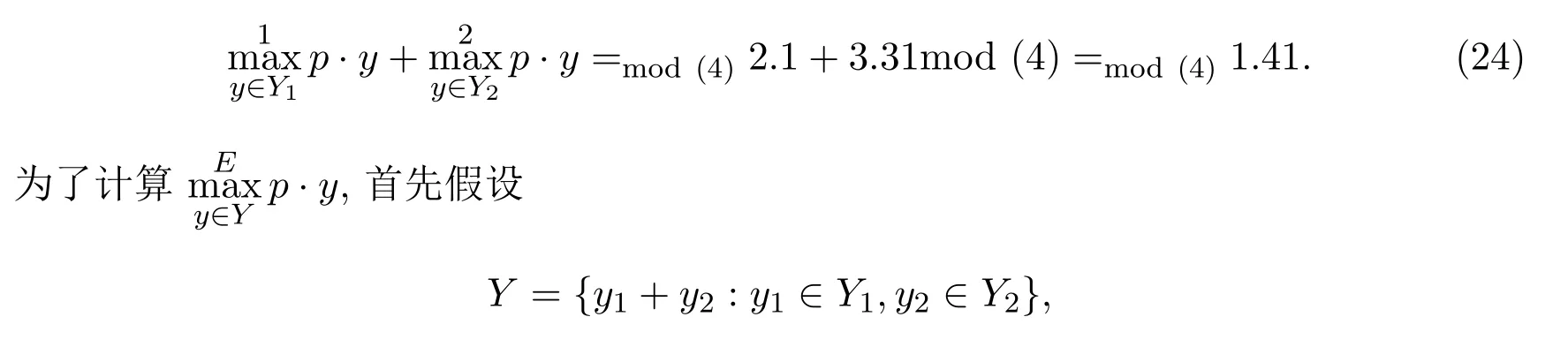
其中这个双生产者经济体的实数序关系等于≤E=≤mod(4).也就是说，Y中的元素以Iij+Jkl的形式给出，i，j，k，l=1，2.公式p·y=p·y1+p·y2mod(4)的计算结果如表1所示.其中左边第一列为生产者1的取值，最上面一行为生产者2的取值.

表1 计算的结果

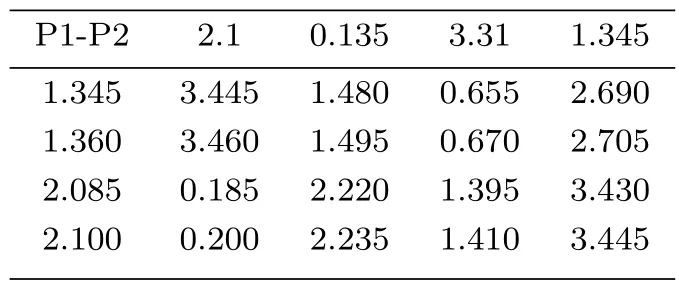
表1 计算的结果

P1-P2 2.1 0.135 3.31 1.345 1.345 3.445 1.480 0.655 2.690 1.360 3.460 1.495 0.670 2.705 2.085 0.185 2.220 1.395 3.430 2.100 0.200 2.235 1.410 3.445

其中序关系≤E由≤mod(4)给出.

上述讨论，论证表明，就一般的价值观和信念系统而言，等式(21)不成立.

等式(20)和等式(21)不成立的更一般的情况是，一般的经济体不存在任何一个统一的实数序关系≤E.例如，一个小型经济体中的两个生产者1和2的实数序关系分别为≤mod(3)和≤mod(4).那么在这个经济中2和3.1两个实数就不能排序.因为这两个生产者各自的序关系不一致.具体地说，有

所以方程(20)不能用于定义任何与每一个生产者的序关系一致的，经济体的统一序关系≤E.

就亚当·斯密于1759年在他的著作《道德情操论》第四部分，第一章中所提出的“看不见的手”而言，这一个结果非常重要.在《道德情操论》中，“看不见的手”描述了个人为自己的利益行事所带来的意想不到的更大社会利益和公共利益[43].在这里，关键是“更大”这个词.它是什么意思?根据上面的讨论，只要存在实数序关系相互不一致的生产者，经济体的序关系≤E一般来说不存在.也就是说，一般而言，在现实生活中的任何经济体中，都没有一种普遍接受的方式来说明“更大的社会福利和公共利益”是什么意思，因为在这样一个大规模的经济系统中，总存在个体价值观和信仰体系相背的生产者.所以这些生产者的实数序将是不一致的.换句话说，上面的分析证实了Joseph E.Stiglitz[44]根据文献[45]所声称的那样:看不见的手通常不存在.

6 结束语

近年来理论家和实践工作者都发出了非常响亮而有意义的呼吁:重建当代流行的商业和经济理论.之所以这样呼吁，是因为理论的结果与预测通常不能为实际生活，生产目的提供及时或者正确的指导.对于相关讨论，参见文献[3，33]以及本文介绍章节中给出的Paul Krugman和Paul De Grauwe的评论.为了积极回应这些呼吁，本文基于公司的自然天赋[6，36]:自我意识，想象力，良心，和自由意志，对广泛接受的生产者理论[40-41]进行了系统，细致的检验，并且通过逻辑推理得到了一系列更加现实的理论结果;从而向这一宏大的目标迈出了有意义的一步.

之所以选择企业的自然天赋作为推理和分析的基础，是因为认识到欧洲16至17世纪的科学革命与当前的大数据时代存在相似之处.在前一种情况下，出现了两种重要的数学理论:统计学和微积分.因此出现了两种方法论方法:基于统计学的数据分析，基于微积分的分析推理.对比当代的大数据时代，伴随着当今大数据时代的发展，已经出现了商业分析(business analytics)的理论和方法论方法.联合应用不确定性理论(如模糊集理论，灰色系统等，详情请参见文献[46，p315-323])，信息技术和各种商业理论，这个新的理论和方法论方法正在为决策者生成潜在的，有用的决策信息[47].因此，预计:在当前的大数据时代，应该会出现另一种重要的理论和方法论方法;该理论和方法论方法将与商业分析(business analytics)并行发展.由于当前的商业和经济研究大多处于事实收集或应用现有数学和科学理论的阶段，因此学者们不断地推测，推导出各种不一致的，不相容的经济与商学理论(参见文献[33，第1章]).

通过将商业和经济研究的这种状态与那些在 “正常科学”(normal science)或范式(paradigm)出现之前普遍存在的历史[48]进行比较，通过使用Kuhn[48]对科学史的观察，可以相信:与当代的商业分析(business analytics)相平行地，一个全新的理论和方法论方法应该会出现在商业和经济研究之中.这样推断的原因是:商业和经济研究通常需要检查自反(reflexive)关系[49];其中所有的变量相互影响，因此很难将因变量(如果存在的话)与其他变量区分开来.换言之，如果不发展出全新的理论和相关的方法论方法，将很难继续利用现有的数学和科学理论来充分研究各式各样，层出不穷的商业和经济现象.

通过忽略内部结构，人们抽象出了数和变量的概念.因此自16至17世纪以来，微积分和基于微积分的分析推理得到了成功的发展与应用.现在，通过从每家公司中抽象出自然天赋这个概念，尽管公司有各自不同的价值观和信仰体系，人们仍然可以成功地在商业和经济研究中发展，应用系统科学的理论与方法.基于心理学和社会学的研究[34]，毫无疑问，每个决策者都通过有意识或无意识地使用其背后的价值观和信仰体系来评估可用信息.这就是为什么有理由相信，通过将决策行为追溯到他们的价值观和信念系统，将有助于人们在商业和经济研究中发现，创立所预期的理论和相关的方法论方法.

为了证实上述预期，本文采用集合论的语言来检验生产者理论的一系列7个最基本的定理.由于公司，企业自然天赋的新颖应用，本文令人信服地证明了企业特定实数序关系的存在.这种各自不同的实数序关系反映了一个企业的优先标准，决策方式与另一个企业的差异.也就是说，每一个公司都拥有自己特定的优化标准与方法.对于相关讨论，请参见Hammerton[50]，Van Fleet[51]以及Yang和Andersson[52].除了建立正式的以集合论为基础的结论外，这个结果代表了这项工作对已有文献的另一个重大贡献.

通过强调公司不同的优化标准与方法，本文成功地检验了当每个公司努力通过实现其既定使命来实现其期望的业务成果时，当今所流行的生产者理论中的一些主要结果是如何普遍地，或有条件地成立.由于在推理和逻辑分析中采用的起点与文献中广泛采用的起点截然不同，本文能够重新定义公司的最优生产札(optimal production correspondence)，最低成本生产(minimum cost production)和其他几个关键概念.

这项研究的许多方面都需要未来的，广大学者群体的跟进.例如，本文探讨了两种不同的实数序关系:常规的一种和由模函数定义的一种.然而，现实生活中的管理者和企业家肯定会使用其他方法来优先考虑可供他们决策的替代方案.因此，为了使这项工作与现实生活中的应用更加兼容，学者们需要探索本文中的结果如何在不同的优化标准，方法或不同的价值观和信仰体系下保持它们的可靠性.具体来说，定理3.2-定理3.3，定理4.2-定理4.3，很可能不适用于通过模函数定义的实数序关系的价值观和信念系统.那么，在这样的序关系下，这些结果会是什么样子呢?或者，这些结果将以什么形式出现呢？希望可以在未来的岁月中，有机会与广大的同仁们一起重建经济以及商学上的各种理论，使其更具有现实的可运用性.