周期时滞的种群生物学模型研究综述

楼一均，赵晓强

(1.香港理工大学应用数学系，香港 999077;2.纽芬兰纪念大学数学与统计系，加拿大 A1C 5S7)

1 引言

在理论生态学研究中，两类常用的数学模型可以较好地刻画具有阶段结构的种群密度的动力学演化:基于出生，发育，死亡的积分形式(见方程(1)和方程(2))，以及基于状态(如年龄，尺度等)结构的偏微分方程形式(见方程(3)和方程(4)).本节将对这两类模型以及它们在不同生物背景假设下的约化作简要介绍，更多详细内容可以参阅文献[1-4].为方便阐述，考虑两阶段的最简单形式，如在考虑物种生长时，可以将第一阶段看作不具有生殖能力的幼年阶段，第二阶段为具有生殖能力的成年阶段.其中物种在第一个阶段和第二个阶段位于t时刻的种群数量或者密度分别计为N1(t)和N2(t).接下来介绍基于两种不同思路导出关于N1(t)和N2(t)的方程组.

第一种建模思路是基于对种群中个体的出生，发育及死亡等生态过程进行描述的积分形式.该建模思路可以追溯到Lotka在1907年的工作[5].为了刻画个体在第一阶段的发育率及考虑个体从幼年阶段发育到成年阶段所需时间的差异性[6]，引入逗留时间概率(sojourn function)函数P(a).该函数描述了在t时刻，具有第一阶段停留时间a的个体(也就意味着该个体在t-a时刻进入第一阶段)留在第一阶段的概率.因此该函数P(a)是单调递减的且P(0)=1.假设函数P(a)可微，那么关于以逗留时间为随机变量的概率分布所对应的概率密度函数可以表述为-P′(a)(当P(a)不可微时，相关讨论需用黎曼-斯蒂尔杰斯积分(Riemann-Stieltjes integral))[3].根据函数P(a)，可以计算其它相关的生物学指标，如平均逗留时间以及年龄为a的个体剩余逗留时间的期望(expected remaining sojourn times)为[3-4].考虑在t时刻第一阶段的种群，其数量包含两部分:由0时刻引入并在t时刻仍然逗留在该阶段的个体以及[0，t]时刻新出生并且在t时刻仍然停留在第一阶段的个体.基于此，N1(t)可以表述为

在该表达式中，B(N2(s))代表在s∈[0，t]时刻进入第一阶段的输入率(在此，假设由第二阶段的出生率函数B(·)决定).此外，假设在第一阶段的存活概率函数为Π1(a).在上式中，由初始0时刻引入，逗留并存活在第一阶段的种群数量为

类似地，在第二阶段的种群数量可以表述为

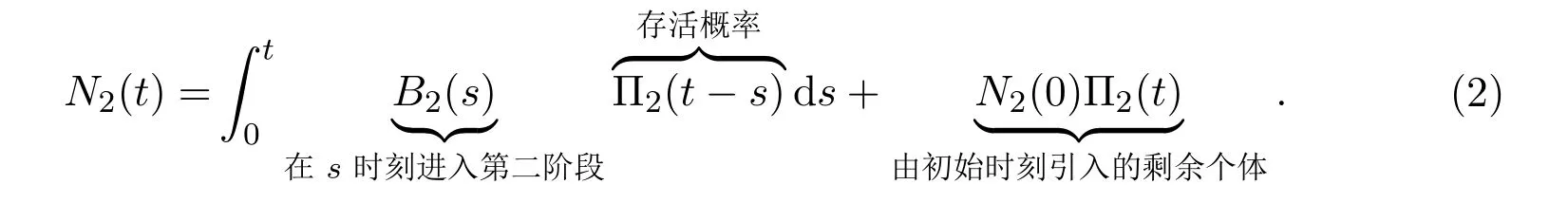
方程(2)和方程 (1)相似，但对于第二阶段，假设逗留概率为 100%，即个体一旦进入第二阶段，将永远停留在该阶段直至死亡(即在第二阶段的逗留时间的概率函数为1).在s时刻输入至第二阶段的发育率[4]为

在上述表达式用到了逗留时间的概率密度函数-P′(a)，可以解释如下:个体在(a，a+h)年龄段离开第一阶段的概率为P(a)-P(a+h).取极限h趋向于零时，可得幼年个体在年龄为a时离开第一阶段的速率为-P′(a).

另一种常用的模型构建思路是基于个体生理特征，如体型大小(body size)和年龄 (age)，建立相应的数学模型.此时，假设函数u(a，t)和v(η，t)为t时刻第一阶段和第二阶段的阶段年龄(stage-specific age)分别为a和η的种群密度.令第一和第二阶段的逗留时间概率函数为P(a)和100%，则t时刻种群数量N1(t)和N2(t)可以分别表述为

根据McKendrick考虑年龄结构种群密度的建模思想[7](也可参阅文献[8-12]，得如下偏微分方程

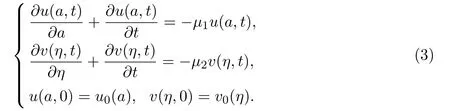
初始时刻的阶段密度分布由初值u0(a)和v0(η)给出.在该系统中，μ1和μ2代表第一阶段和第二阶段的个体死亡率(假设阶段年龄为a的个体在每个阶段的生存概率Πi(a)符合 Πi(a)=e-μia，则.边值条件u(0，t) 和v(0，t) 分别代表在t时刻进入第一和第二阶段的种群密度，则

当停留函数取特定的分布函数时，基于积分形式(方程(1)和方程(2))和偏微分形式(方程(3)和方程(4))的阶段结构模型可以约化为数学上易于处理的常微分方程或者时滞微分方程系统.如假设P(a)服从Erlang分布(即Gamma分布中形状参数为整数n的情形，两类模型都可以约化为n+1个方程的阶段结构模型[4].其中第一阶段种群数量可以看作n个不同子阶段的累积.特别地，当n=1以及假设个体在第一阶段的平均停留时间为时，逗留函数服从指数分布，即P(a)=e-λa.此时有如下阶段结构模型

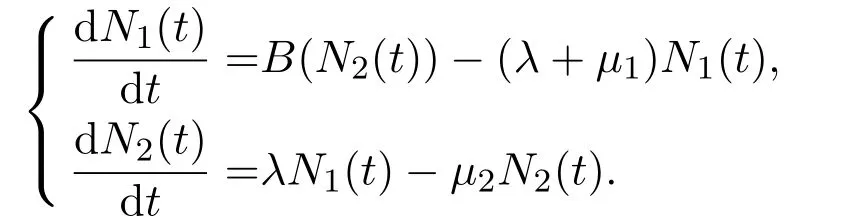
当在第一阶段的停留函数P(a)符合狄拉克(Dirac)分布，即

其中，τ为第一阶段的平均停留时间.阶段结构模型(方程(1)和方程(2)，或方程(3)和方程(4))可以约化为如下具有时滞τ的时滞微分方程系统

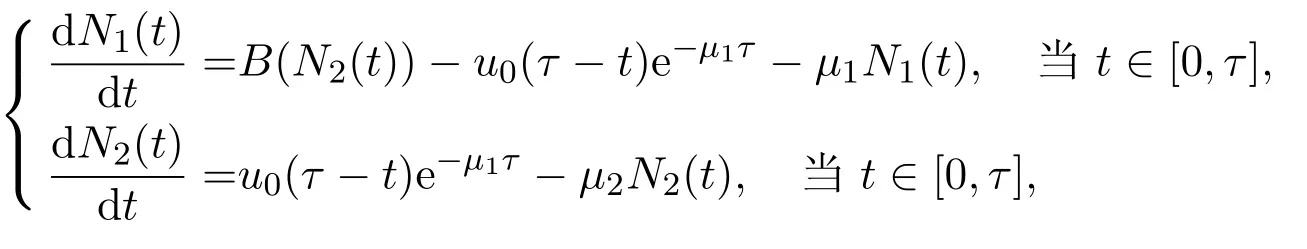
以及

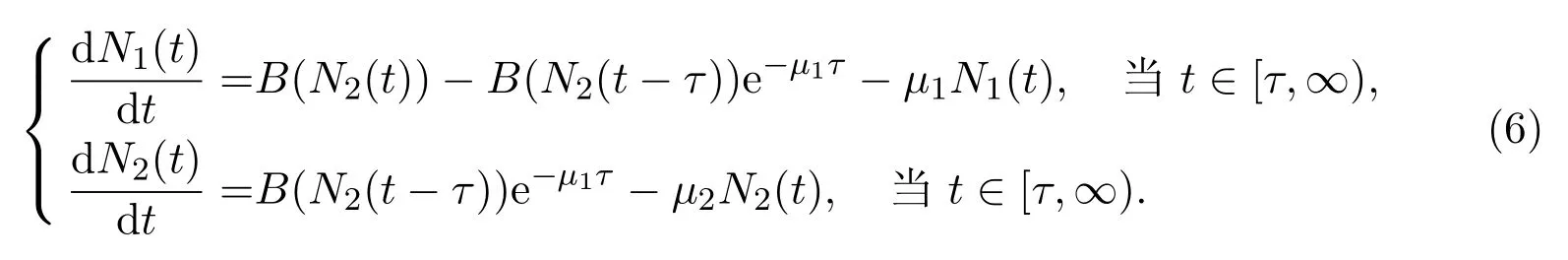
其中u0由积分形式或者偏微分形式的初值决定.当研究种群数量N1(t)和N2(t)的长期动力学行为时，只需要在适当的给定初值意义下研究系统(6).此外，观察到第二个方程可以从整个系统解耦出来，故可首先着重于了解变量N2(t)的动力学性质，即研究如下方程的动力学行为

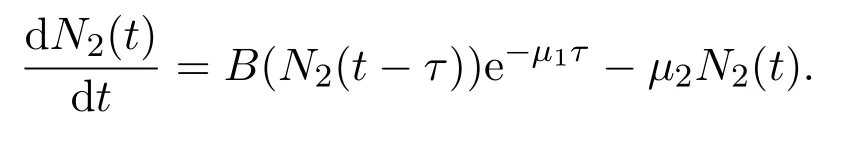
根据N2(t)的动力学性质，N1(t)的动力学行为可以由积分形式(1)得到.

当停留函数P(a)符合狄拉克(Dirac)分布时，每个个体在第一阶段具有相同的固定停留时间τ(逗留时间分布的方差为零).在很多生物系统中，每个存活个体在特定阶段的停留时间τ可能受外界环境影响，而外界环境因素可以由关于时间t的函数给出.由此，发育所需时间用一个关于时间t的函数τ(t)描述更为合适.

在生物学研究中，计算发育所需时间τ(t)也是非常有意义的问题.其中一种方法可以利用发育比率得出[13-14].基于给定时间t所对应的环境条件可以得到所对应的发育比率.如在很多代谢生态学(metabolic theory of ecology)研究中，个体发育比率[15]可以由确定的表达式给出，譬如

其中b0是比率常数，E为活化能常数，k=8.6173×10-5eV K-1为玻尔兹曼常数(Boltzmann constant)，T(t)代表时刻t的热力学温度(绝对温度).假设当个体累积发育比率达至100%时，个体发育至成年阶段.假设t时刻成熟的个体在幼年阶段的停留时间τ(t)，则这些个体在幼年阶段的停留时间段为 [t-τ(t)，t].在此时间段上，个体累积发育比率达至100%.则有

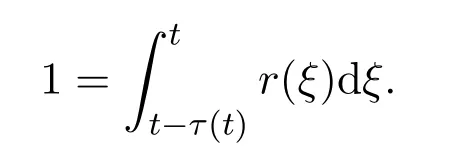
假设任意时刻的发育比率r(ξ)严格大于零，则τ(t)是唯一确定的.同时，如果假设t时刻的温度T(t)是关于t的ω-周期函数，则τ(t)也是周期函数.此外，对该积分形式作微分，得到

在本文中，将展示如何在模型建立时考虑周期性的发育时间τ(t)，以及如何对这些模型进行基本的动力学分析.

2 周期时滞模型的构建及分析

假设t时刻个体发育至第二阶段所需的停留时间为τ(t)，则该个体在第一个阶段的t-τ(t)时刻出生.由此，可以将(5)式中停留函数P(a)拓展至如下时间依赖形式

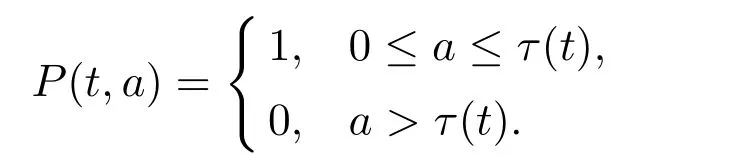
将根据年龄结构模型的框架考虑周期性的停留函数P(t，·).为此，引入多元函数u(a，t)表示t时刻具有生理年龄为a的种群密度.考虑周期性的外界环境对个体出生率，死亡率等的影响，则有如下偏微分方程

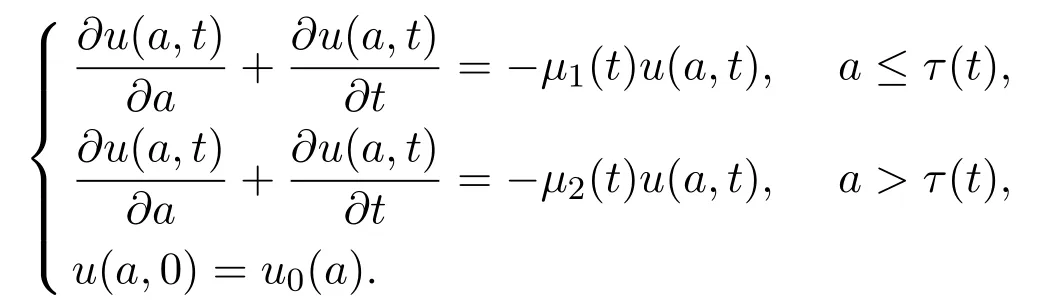
因此，在t时刻种群数量N1(t)和N2(t)可以分别表述为

进一步，对N1(t)和N2(t)求导可得如下微分方程

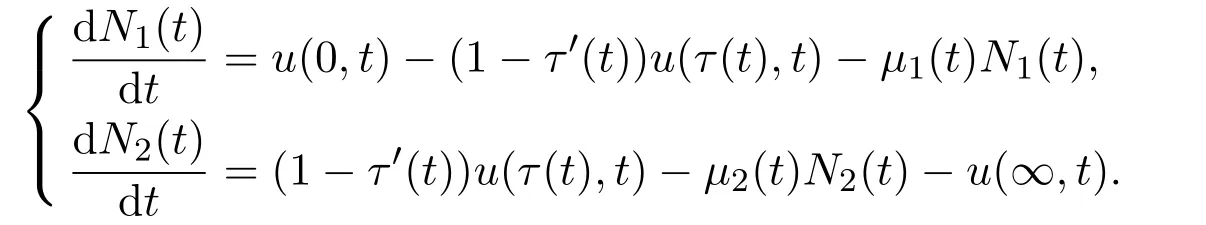
由于没有个体可以永恒存活，故假定具有无穷年龄的种群密度为零，即u(∞，t)=0.假设t时刻的出生率u(0，t)为依赖于时间t和成年物种数量N2(t)的函数，即

此外，需要计算在t时刻的发育率 (1-τ′(t))u(t，τ(t)).此项可以由沿特征线积分法通过u(0，t-τ(t))=B(t-τ(t)，N2(t-τ(t)))表述.为此引入带参数s的函数Vs(t)=u(t-s，t)，其关于时间变元的导数当t-s≤τ(t)时满足如下方程

求解该线性常微分方程得到

当t≥:=max{τ(t)}时，设参数值s=t-τ(t)，则

因此，当t≥时，种群动力学可以由下面的时滞微分方程系统描述

观察到第二个方程可以从整个系统解耦出来

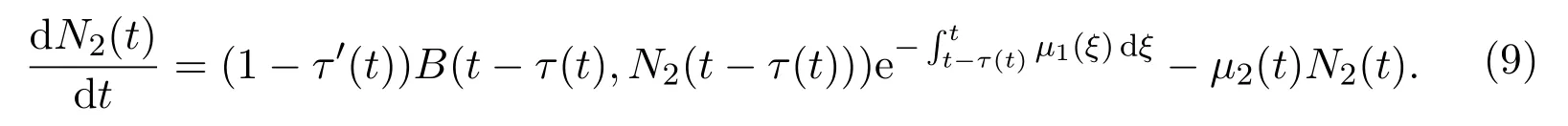
在该模型中，t时刻的发育率为

此外，文献[16]给出了另一种导出此发育率的思路.为此，作者引入发育水平变量q来刻画个体在发育过程中的差异性.假设q=0以及q=1分别代表新出生和发育到成年阶段时的发育状态，则在t时刻的种群密度ρ(q，t)的变化率可以表述为[17]

在上述方程右端，J(q，t)描述在t时刻的发育流束(也称通量).考虑周期性的发育速率，则J(q，t)=r(t)ρ(q，t)，其中r(t)类似于方程 (7)中的发育比率.因此，有

其中该方程的边界条件由出生率给出ρ(0，t)=B(t，N2(t)).对(11)式沿特征线积分可得

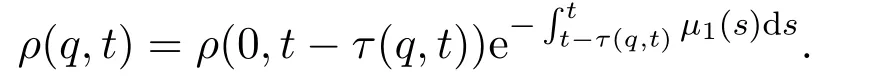
其中τ(q，t)满足，即在时间段 [t-τ(q，t)，t]上的累积发育水平为q.令τ(t)=τ(1，t)，则有

据此，t时刻的发育率可以表述为

另一方面，由于τ(t)满足，则根据方程 (7)，发育率 (10)也可写为

在该模型中，假设出生率函数B(t，N2)，单位死亡率μ1(t)和μ2(t)为正值函数.所有参数为关于时间t的ω-周期函数.此外假设出生率函数B(t，N2)满足下列条件:

(A1)出生函数B(t，N2)是关于N2变量的利普希茨连续函数，且关于变量N2单调递增.此外，对于任意t，B(t，0)≡0，以及B(t，N2)有界;

(A2) 函数B(t，N2) 可以表示为B(t，N2)=b(t，N2)N2，这里单位出生率b(t，N2)关于N2是严格单调递减的.

2.1 模型解的基本性态

对于给定初值N2(θ)=ψ(θ)，θ∈[-，0]，方程(9)可以表述为

则关于方程(9)解的存在唯一性可以由时滞微分方程的一般理论得出[18-19].此外，关于 1-τ′(t)的表达式 (7)确保了 1-τ′(t)＞0，则周期时滞模型 (9)的发育率非负，那么根据文献[47，定理5.2.1和注记5.2.1]可以推导出N2(t)的正性以及有界性(基于出生率的假设(A1)).为了得到系统(9)中N1(t)的正性，将此变量用积分形式表示为

鉴于该积分中被积函数的正性以及有界性，立即可得N1(t)的正性和有界性.具体的证明细节可见文献[13].

2.2 基本再生数

基本再生数(basic reproduction number)可以计算在无密度制约因素时，单个成年个体在一生中能产生下一代的平均值.一般情况下，可以用基本再生数预测种群是否会灭绝.数学上可以由特定空间上的下一代算子(next generation operator)的主特征值所定义.近二十年来，关于基本再生数的数学理论得到了长足发展[21-28].对于含时滞的周期微分方程系统(9)，可以用文献[29]的方法定义其基本再生数.为此，先对方程(9)在零解处进行线性化可得

对任意φ∈X，定义

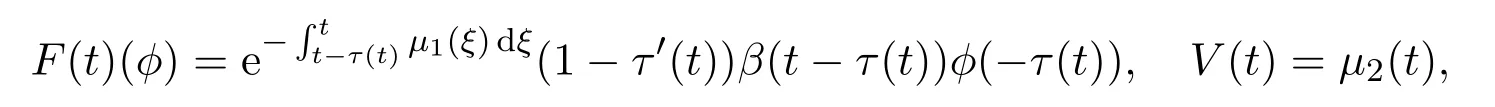
则F(t)和V(t)为关于t的ω-周期函数.此外线性系统(12)可以记为

可以将F(t)看作是出生率相关的泛函，而V(t)可以用来刻画成年个体的存活概率.定义Z(t，s)，t≥s为由线性方程定义的发展算子，即该算子满足

尤其在当下社会，随着社会生产力的提高，人民对物质文化生活的期望也日益提高，会有更多的社会力量去关注“精神食粮”，比如图书馆文献资源建设的情况。这种具有公益性和慈善性的行为更是对社会的和谐发展，公民的人生观、价值观有着积极的指导意义。本文选取在中国历史上比较具有代表性的阶段——民国时期，对图书馆文献捐赠的历史进行梳理与探析。

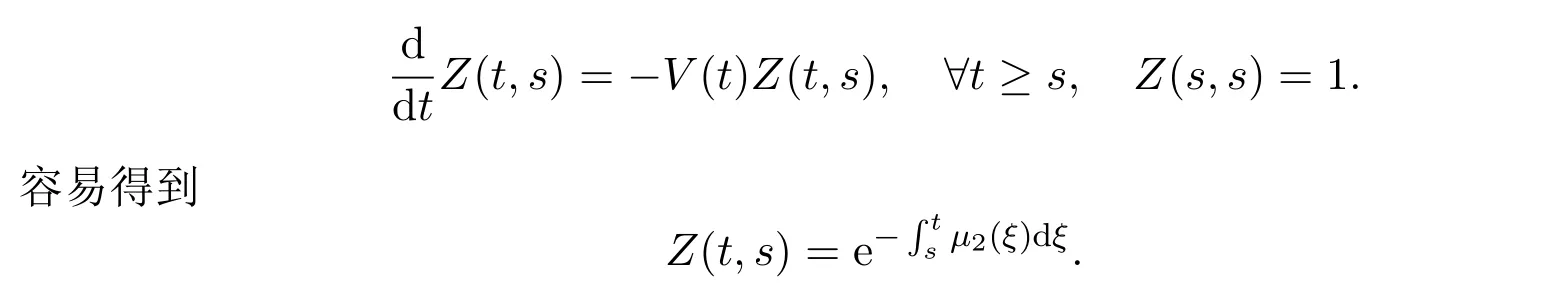
此外，定义Z(t，s)的指数增长界

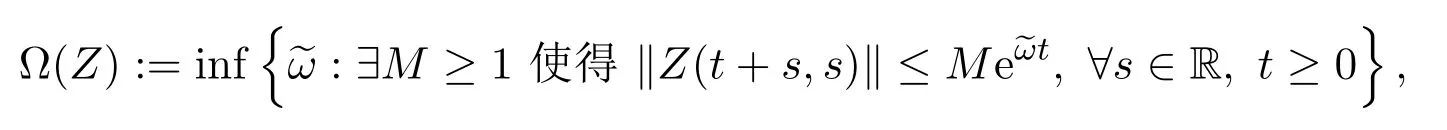
(C1)对任意t≥0，F(t)X+⊆R+;

(C2)Ω(Z)＜0.

定义所有从R到R的连续ω周期函数空间为Cω.对此空间赋予最大模范数，则该空间为巴拿赫空间.此外，定义正锥.假设v∈Cω为周期性的初始分布，则F(t-s)vt-s(t≥s≥0)为t-s时刻新发育进入第二阶段的种群密度，Z(t，t-s)F(t-s)vt-s为t-s时刻进入第二阶段，并存活至t(t≥s)的种群密度.由此

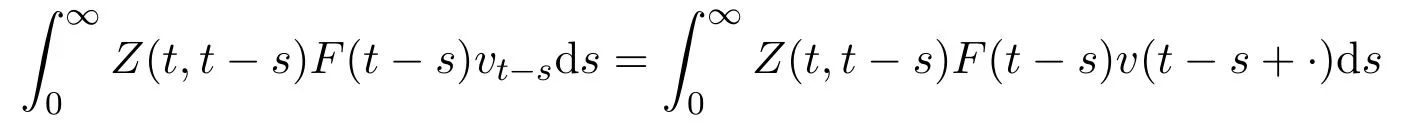
给出了所以初始分布为v(·)在一生中所累积的下一代数目.据此，下一代算子L:Cω→Cω可以定义为

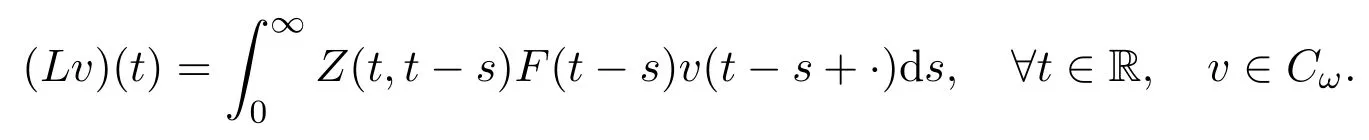
根据文献 [29]中的理论，可以将基本再生数定义为该算子的谱半径 (spectral radius)，即R0:=r(L).

引理 2.1R0-1和r(W(ω))-1同号.

2.3 不同的相空间

对于模型(9)，当考虑X为相空间时，系统解的存在唯一性，有界性，以及解对初值的连续依赖性等结论可以由时滞微分方程系统的一般理论直接得出[18-19].但是当考虑相空间为X时，解映射是最终单调(monotone)而非强单调(strongly monotone)的.为了证明全局稳定性等结论，有时需要利用解映射的强单调性(如文献[30，2.3节]).为此，引入另外一个相空间如下

则 (Y，Y+)为有序巴拿赫空间.对于此新空间中的u:[-τ(0)，+∞)→R和t≥0，记ut∈Y为

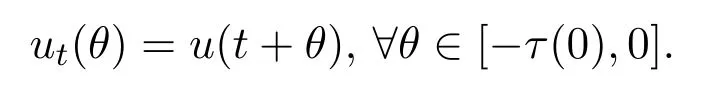
则在此新空间下，有如下结论，其具体证明类似于文献[13]，故此处予以省略.

引理 2.2假设 (A1)成立，对于任意φ∈Y+以及t∈[0，∞)，方程 (9)存在以u0=φ为初值的唯一的非负解u(t，φ).

注 2.1根据解在不同相空间X和Y上解的唯一性可以得知:对于任意ψ∈X+和φ∈Y+，如果ψ1(θ)=φ1(θ)，∀θ∈[-τ(0)，0]，则方程 (9)以初值u0=φ的解u(t，φ)和以初值v0=ψ的解符合u(t，φ)=v(t，ψ)，∀t≥0.

引理 2.3定义t≥0时刻解映射Qt(φ)=ut(φ)，∀φ∈Y+，则Qt是在空间Y+上的ω-周期半流.它符合下面三条性质:(i)Q0=I;(ii)Qt+ω=Qt°Qω，∀t≥0;以及 (iii)Qt(φ)关于变量 (t，φ)∈[0，∞)×Y+连续.

进一步，周期半流Qt是最终强单调以及次齐性的，该结论由如下两个引理给出:

引理 2.4假设 (A1)成立，对于Y+空间上两个初值φ和ψ，如果满足φ＞ψ(即φ≥ψ但是)，则方程(9)通过这两个不同初值u0=φ和v0=ψ的解u(t)和v(t)满足u(t)＞v(t)(当t＞时).也就意味着当t＞2时，Qt(φ)≫Qt(ψ).

引理 2.5假设 (A1)及 (A2)成立，对于空间Y中的任意初值φ≫0和任意γ∈(0，1)，当t＞时，解满足u(t，γφ)＞γu(t，φ).因此对于任意n符合nω＞2，庞加莱映射 (Poincaré map)Qω满足.

对于给定t≥0，定义G(t)为线性周期系统(12)以Y为相空间的t时刻解映射，即根据系统(12)过初值z0=φ∈Y的解z(t，φ)定义G(t)φ=zt(φ).则下面的结论显示系统(12)在不同相空间X和Y具有相同的线性稳定性.

引理 2.6在相空间X中的庞加莱映射 (Poincaré map)W(ω)和相空间Y上的庞加莱映射具有相同的谱半径，即r(W(ω))=r(G(ω)).

根据引理2.1，基本再生数可以决定系统以X为相空间的稳定性.结合上述引理可得基本再生数R0也可以决定线性系统以Y为相空间的稳定性.利用解映射在相空间Y上的最终强单调性(引理2.4)及次齐性(引理2.5)，结合单调动力系统相关理论(见文献[30，定理2.3.4和引理2.2.1])，可得系统(9)的全局动力学结论:

定理 2.1(i)当R0≤1时，零平衡点在Y+相空间中是全局稳定的.

(ii)当R0＞1时，系统 (9)存在一个唯一的ω-正周期解，该正周期解对于所有初值在Y+{0}中是全局稳定的.

根据N1(t)关于变量N2(t)的表达式

可以进一步得知关于系统(8)中变量N1(t)的动力学行为.从而整个系统的动力学行为可以表述如下:

定理 2.2(i)当R0≤1时，(0，0)是全局稳定的.

(ii)当R0＞1时，系统(8)存在一个唯一的ω-正周期解该正周期解对于所有非平凡解是全局稳定的.

3 不连续周期时滞

具有周期时滞的模型(8)带有正的修正项1-τ′(t).当时滞关于时间t的导数不存在，即周期时滞函数不可微时，该模型不成立.根据方程(7)，直觉上如果在一个ω周期内某个时刻的发育率为零，则1-τ′(t)不存在.此时基于模型(8)的建模思路不适用.事实上，当生物个体进行滞育(diapause)时，个体的发育比率为零，此时需要用其它方式推导出合理的数学模型.在本节中，主要展示文献[31]中关于描述滞育现象的数学模型.

滞育是指动物受环境条件的诱导所产生的一种静止状态，该生物学策略使动物有能力在不利的季节条件下存活，并与有利的季节条件同步以有效利用资源.文献[31]以蚊子的滞育现象为研究对象，特别是考虑了两种不同蚊子物种的滞育策略:库蚊(Culex)以成虫形式滞育而伊蚊(Aedes)以卵形式滞育.对每一种滞育策略推导出不同的两个数学模型.特别地，这两个模型可以统一为如下一个模型.假设物种在每个时间周期只包含一个坏的环境季节，也即意味着物种在该季节进行滞育.基本的建模思路是将一个周期时间段分为三个时间区间:滞育前时间段 (pre-diapause period)，滞育时间段 (diapause period)，以及滞育后时间段 (post-diapause period).记每个时间段分别为T1:=[n，n+1-τ-τd]，T2:=[n+1-τd-τ，n+1-τ]和T3:=[n+1-τ，t≤n+1].为了阐述方便，假设周期为一年，其中n代表第n年，τ和τd代表正常季节物种所需的发育时滞及坏环境季节的时长(每一年中T2时间段时长).因此可以在每个时间段上分别建立不同的系统来刻画种群动力学.

在时间段T1:=[n，n+1-τ-τd]上，假设环境因素是不变的，则种群的密度变化仍符合系统(6)的描述，即

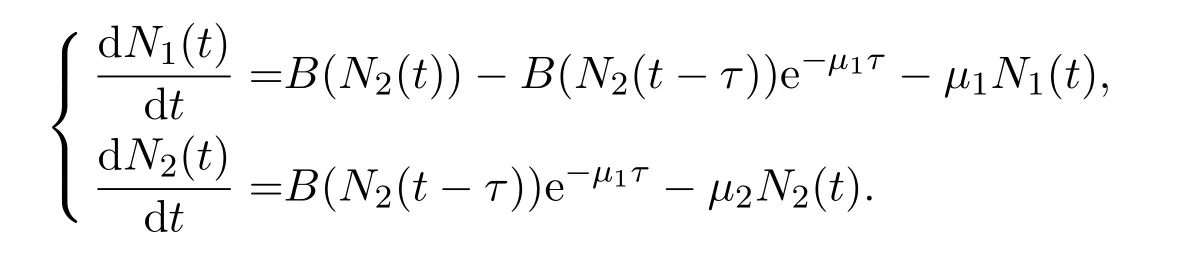
在时间段T2:=[n+1-τd-τ，n+1-τ]上，生物个体进行滞育以在极端恶劣环境因素下生存，则幼年个体发育率急速降低，其它的生理活动也大大降低.假设在此时间段上，幼年个体不发育(即从幼年阶段到成年阶段的发育率为零)以及成年个体不进行生育活动.此外，幼年和成年会受到不同于正常时间段的死亡率影响.基于此，可以用下面系统刻画种群在该时间段上的动力学:

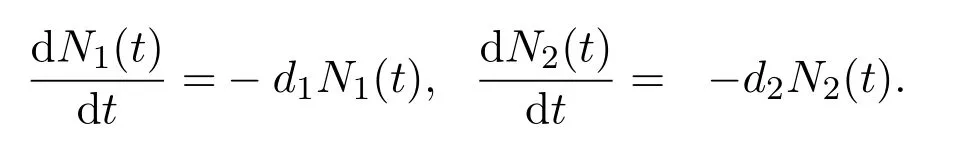
特别地，当物种以幼年个体的滞育为生存策略时(如伊蚊)，假设在此时间段上成年个体的死亡率极高，即d2≫0.而当成年个体滞育时(如库蚊)，则设此时间段上幼年阶段死亡率极高，即d1≫0.

在时间段T3:=[n+1-τ，n+1]生物个体能正常生长，发育及生育.但由于T3时间段的长度为τ，则此时间段上所有发育为成年的个体都经历了T2时间段，也即意味着所有发育个体都经历了τ+τd发育时滞，同时所对应的生存概率为 e-μ1τ-d1τd.利用系统(6)的建模思路，该时间段上的种群密度变化可以描述为

类似于系统(8)的分析思路，变量N2(t)所对应的方程同样可以从模型中解耦出来.因此，可先对N2(t)变量进行分析以讨论整个物种的种群动力学行为，即先研究如下系统:

在该系统中，n∈N代表第n年.当考虑每个时间段的端点时，考虑的是单边导数.由于一年内不同时间区间T1及T3上的时滞分别为τ和τ+τd，而在T2时间段上的时滞可以选取任意大于等于零的数值，所以可以将时滞看作关于时间t的周期函数，而该周期函数是不连续的.

对于出生率函数以及死亡率等模型参数，引入下面常用的生物假设[32]:

(H1)出生函数B(N2)是非负的利普希茨连续函数，并且是关于变量N2的单调递增函数.此外，B(0)=0.存在使得B(N2)e-μ1τ＞μ2N2当，以及B(N2)e-μ1τ＜μ2N2当.

(H2)2τ+τd＜1.

上述条件(H1)为常用的生物假设.此外，蚊子滞育由极端寒冷或者干旱季节所引起，当环境条件变好时，滞育期结束[33].一般地，滞育期对于不同的蚊子物种以及不同地理位置可以维持 3-5个月，即τd在3-5个月取值.同时，幼年蚊子的发育周期较短，基本维持在2-4周[34]，即τ在2-4周取值.从这个意义上，当考虑以年为时间单位时，假设(H2)是合理的.

引入空间Y=C([-τ，0]，R)，对任意φ∈Y，定义范数，则 (Y，‖·‖)为巴拿赫空间.对于给定初值φ∈Y+:=C([-τ，0]，R+)，关于N2(t)变量的系统(13)解的存在唯一性可以通过在不同时间段T1，T2以及T3上分别进行讨论.假设系统在t时刻的解为u(t，φ).根据时滞微分方程常用记号ut(θ，φ)=u(t+θ，φ)，∀θ∈[-τ，0]，有u0=φ.此外，N2(t)变量的正性可以通过分析积分形式得到

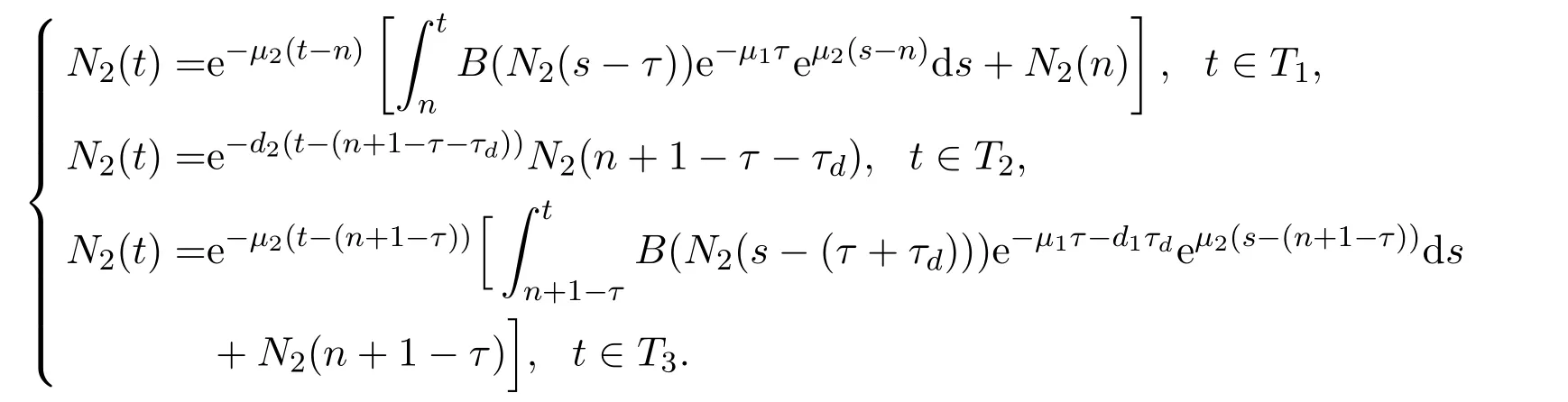
综合这些分析，并利用文献[31]的证明细节，可以得到如下关于系统(13)解的存在唯一性以及正性的结论.

定理 3.1假设条件(H1)和条件(H2)存在，则对任意φ∈Y+及初值u0=φ，对所有时刻t∈[0，∞)系统(13)存在唯一的非负及有界的解u(t，φ).

定义 Φt为系统 (13)在集合Y+上的解映射，即如果u(t，φ)是系统 (13)过初值u0=φ∈Y+的解，则 Φt(φ)(θ)=ut(θ，φ)=u(t+θ，φ).

引理 3.1解映射Φt为如下意义下的1-周期半流:(i)Φ0=I，此处I为恒等映射;(ii)Φt+1= Φt°Φ1，∀t≥0;(iii)Φt(φ)关于 (t，φ)∈[0，∞)×Y+是连续的.

此外，也可以证明该周期半流是最终强单调及严格次齐性的.相关证明可以参阅文献[31].

引理 3.2对于Y+中给定的两个初值φ和ψ，假设φ＞ψ(即对于所有s∈[-τ，0]，φ(s)≥ψ(s).此外)，则通过这两个初值的系统 (13)的解u(t，φ)和v(t，ψ)当t＞τ+τd时满足u(t，φ)＞v(t，ψ).这意味着当t＞2(τ+τd)时，Φt(φ)≫Φt(ψ).

假设出生函数还满足如下条件:

(H3)出生函数B(N2)可以表示为B(N2)=b(N2)N2以及单位出生率b(N2)关于N2是严格单调递减的.

则在额外假设(H3)下，解映射所定义的周期半流是严格次齐性的.

引理 3.3对于Y+中的任意函数φ≫0以及λ∈(0，1)，当t＞τ+τd时，有u(t，λφ)＞λu(t，φ).这意味着当整数n满足n＞2(τ+τd)时，.

基于假设(H1)，系统(13)有一个种群灭亡平衡点0.在此平衡点线性化可得如下线性系统:假设P(t)为线性系统(14)在Y+上的解映射.则可以根据庞加莱映射(Poincaré map)P(1)的谱半径，记作R，描述线性系统的稳定性.此外，根据单调动力系统理论(如文献[30，2.3节])以及引理3.2-引理3.3，可以得到如下全局动力学结论.

定理 3.2对于系统(13)，假设条件(H1)-条件(H3)成立，则有如下结论:

(i)当R≤1时，0平衡点在Y+中是全局渐近稳定的.

(ii)当R＞1时，系统存在 1-周期解M*(t)，该周期解相对于Y+{0}是全局渐近稳定的.

通过将N1(t)表示为关于N2(t)的积分形式，则可以得出类似于定理2.2中关于变量N1(t)的全局动力学行为.

在本节最后，介绍一些具有周期时滞的相关研究进展.当系统中的非固定时滞为时间的函数τ(t)，模型往往带有额外修正项1-τ′(t)[35-37].该项也常见于当时滞由模型变量定义 (state-dependent delay)的系统中[38].关于该项的正性，即 1-τ′(t)＞0，除了可以通过商形式(7)说明外，文献[35]给出了更多实际问题中的讨论.事实上，生物文献更多地将该项写成两个特定时间发育比率的商的形式(7)[39].

这两种建模思路以及相关模型分析技巧在最近的研究中得到极大的发展.这些想法可以扩展至其它具体物种或者有多个阶段的种群动力学研究，如考虑由季节性变化引起蜱虫各阶段发育时滞的周期性变化及其对蜱虫种群动力学的影响[40]，周期发育时滞的海虱(Salmon lice)生长的阶段结构模型[41]，多个周期时滞的阶段结构蚊子种群模型[42]等.此外，在疾病传播研究中，很多疾病的潜伏期(latency period)可能受外界环境影响.譬如温度变化可以引起蚊子体内疟原虫的发育率变化，因此导致的周期性蚊子外潜伏期 (extrinsic incubation period)时滞对疟疾传播具有巨大的潜在影响.鉴于此，可以在疾病传播模型中考虑周期性潜伏期时滞，如周期潜伏期的SEIRS模型[43]，周期性的蚊子外潜伏期时滞的疟疾传播模型[16]，具有周期外潜伏时滞的血吸虫病模型[44]，周期时滞的基孔肯雅热 (chikungunya fever)模型[45-47]，周期潜伏期的蓝舌病 (Bluetongue)传播模型[48]，周期外潜伏期的西尼罗河病毒传播模型[49]，周期外潜伏期及垂直传播的西尼罗河病毒传播模型[50]，受温度影响的周期性潜伏期时滞的手足口病 (hand，foot and mouth disease)疾病传播模型[51]，具有周期性潜伏期的黄龙病(Huanglongbing)模型[52]，以及带有周期性潜伏期的蝙蝠传播狂犬病(bat-borne rabies)模型[53]等.

文献[54]进一步将周期时滞函数推广至概周期函数，用于研究概周期生态坏境下具有阶段结构的种群动力学.此外，也可以在种群生物系统中考虑生物个体的空间移动，从而研究具有周期时滞和空间移动的种群生物系统.

4 考虑个体空间移动的周期时滞模型

将拓展上一节中的具有可微或不连续周期时滞模型，同时考虑生物个体在空间上的移动.主要通过文献[55-56]的一些结论来展现典型的建模思路以及相关数学结论.

4.1 具有空间移动及可微周期时滞的媒介疾病传播模型

为了研究空间异质性，媒介(如蚊子)传播疾病中温度敏感的内潜伏期(intrinsic incubation period)和外潜伏期(extrinsic incubation period)，以及其它季节性变化等多种因素对疾病传播的影响，文章[55]提出了一个具有周期时滞的非局部反应扩散系统.该模型主要描述宿主(host)和媒介(vector)的各类仓室种群密度在空间Ω上的动力学变化.将宿主分为易感类 (susceptible)，潜伏类 (exposed)，感染类 (infectious)以及康复类(recovered)，这些类别在时刻t空间位置x上的密度分别为Sh(t，x)，Eh(t，x)，Ih(t，x)以及Rh(t，x).此外，将媒介种群分为易感类，潜伏类，感染类，其密度的时空分布分别为Sv(t，x)，Ev(t，x)和Iv(t，x).假设媒介 (如成年蚊子等)的生命周期较短，故不考虑感染媒介康复的情况.则宿主和媒介总密度分别为

根据病原体在宿主和媒介之间的传播途径以及宿主和媒介的种群生长特征，同时考虑宿主和媒介的移动，可以写出如下系统:

这里的下标h和v分别代表宿主(host)和媒介(vector)相关变量或参数.模型参数的具体意义可见表1.模型(15)中，感染项

表1 模型(15)中参数的生物学意义

中b代表单位时间内每个媒介在宿主上的叮咬次数，h代表每次叮咬从感染媒介到易感宿主的感染概率而v代表从感染宿主到易感媒介的感染概率.空间异质性对物种生长和疾病的传播影响由依赖于空间变元x的参数体现，而个体的空间移动由宿主扩散系数Dh以及媒介扩散系数Dv描述.此外假设个体不能穿越边界，故对此偏微分系统，给定诺伊曼边界条件(Neumann boundary condition).

模型 (15)右端Mh(t，x)和Mv(t，x)分别代表新增感染宿主和媒介的密度变化率，描述所有刚经历潜伏期从潜伏类转化为感染类的转化率.该转化率类似于模型(8)中的发育率(10)，用于描述相应个体在某一个阶段经历一定时间段至下一个阶段的转化率.由于考虑温度等季节性变化对潜伏期的影响，假设潜伏期是关于时间t的周期函数.通过考虑宿主在潜伏期[t-τh(t)，t]的空间移动可以导出Mh(t，x)的表达式.为此假设q为刻画宿主个体感染水平的某种度量，并且q在t时刻的变化率为γh(t)(依赖于t时刻的温度T(t))，即.则可以用q=qE代表宿主从Sh类刚转化为Eh类时的感染水平，而q=qI代表将从Eh类转化为Ih类时个体的感染水平.假设ρ(q，t，x)代表在t时刻x位置具有感染水平q的种群密度，则新增具有感染性的宿主的变化率为Mh(t，x)=γh(t)ρ(qI，t，x).此外，从易感宿主转化为潜伏类宿主的感染项给出具有qE感染水平的种群密度:βh(t，x)Sh(t，x)Iv(t，x)=γh(t)ρ(qE，t，x).下面将主要展示如何通过计算ρ(qI，t，x)得到Mh(t，x)的表达式.为此，需要刻画ρ(q，t，x)的变化情况.类似于(11)式中的讨论，考虑个体的扩散系数Dh，假设J(q，t，x)为q方向在t时刻x位置的通量，则有如下方程

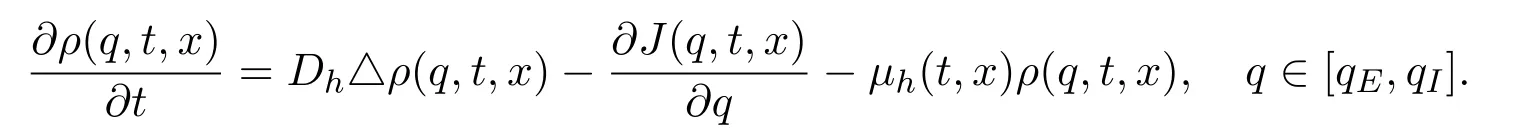
由于J(q，t，x)=γh(t)ρ(q，t，x)，则有

方程(16)的边值条件由下式给出

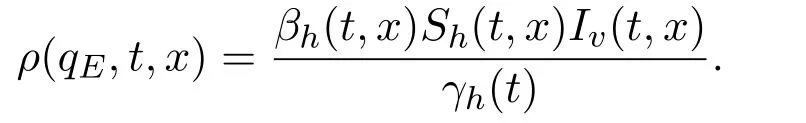
为解上面的方程(16)，引入关于时间t的新变量

由于该函数严格递增，其反函数t=h-1(η)存在.据此定义

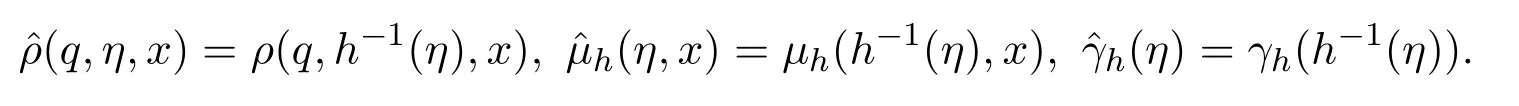
方程(16)可以重写为

设V(s，x)=(s+q-η，s，x)，则有

由于q∈[qE，qI]，η-(q-qE)≤η，从而

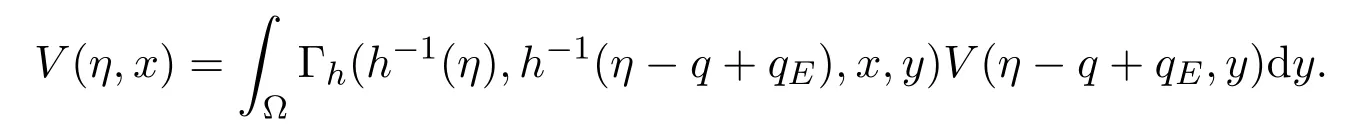
在上述表达式中，Γh(t，t0，x，y) 是由方程在诺伊曼边界条件下定义的格林函数(Green function).因此

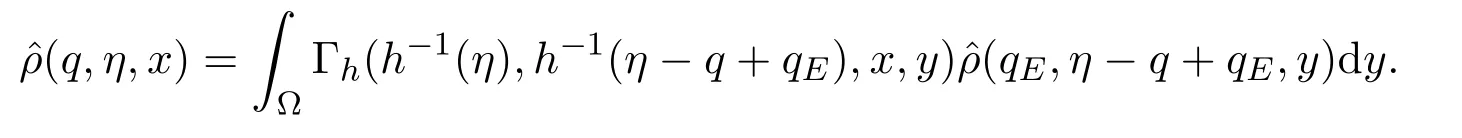
假设τ(q，t)代表在t时刻从初始感染水平qE到达感染水平q所需的时间(即个体的感染水平在时间段[t-τ(q，t)，t]上从初始感染水平qE增加到q).考虑到则有

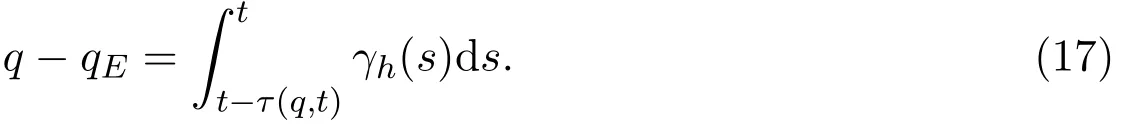
进一步，得到

由于当感染水平为qI时，个体从潜伏类发育到感染类，故在t时刻进入潜伏类的个体所需的潜伏期为τh(t)=τ(qI，t).从而

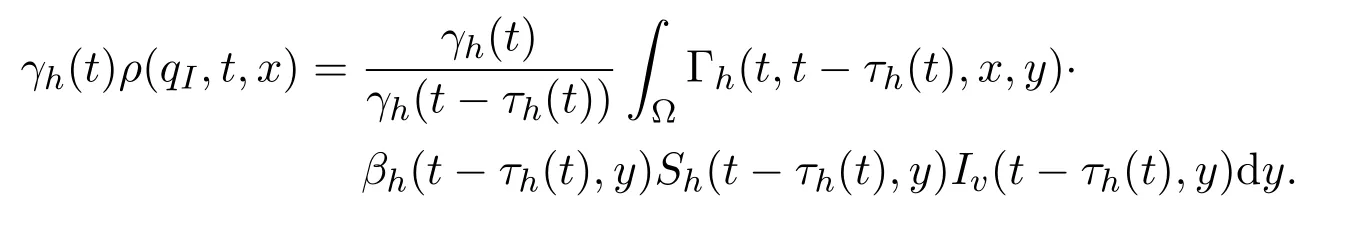
此外，在方程(17)中设q=qI，则有

对该式求关于t的导数得到

类似地，Mv(t，x)的表达式也可以通过分析媒介在潜伏期[t-τv(t)，t]的空间移动得出:

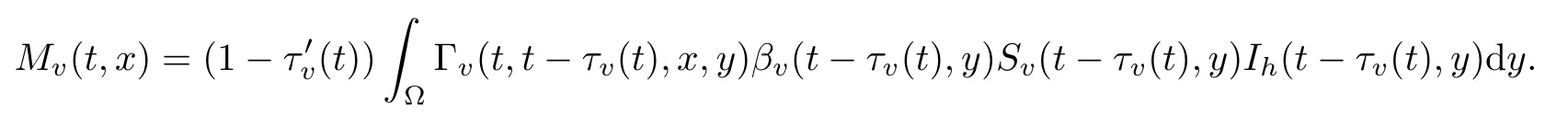
其中 Γv(t，t0，x，y) 为由方程以及诺伊曼边界条件所定义的格林函数.将Mh(t，x)以及Mv(t，x)代入方程组 (15)，则得到具有非局部周期时滞的反应扩散系统.在此系统中，周期时滞描述了由季节性温度条件决定的外潜伏期τv以及内潜伏期τh.

文献[55]针对模型(15)做了详细的分析，内容主要包括模型解在给定的生物假设下的全局存在性以及正性，疾病传播基本再生数的定义，以及由基本再生数刻画的疾病传播的阈值结论:当基本再生数小于1时，疾病不能传播;而当该数大于1时，疾病在空间上持续传播.此外，当所有参数为常数时，进一步得到了当基本再生数大于1时正平衡点的全局吸引性.该文还利用参数对温度的依赖关系，拟合出周期参数并进行有意义的数值模拟.更多相关结论见文献[55].

4.2 具有空间移动及不连续周期时滞的种群模型

对于不连续周期情形(如考虑物种的滞育现象)，也可以将模型(13)进行拓展以考虑个体在空间上的移动.在此，主要总结文献[56]的模型以展示关于幼年成年两个阶段的种群密度N1(t，x)和N2(t，x)的动力学模型.对于第n年正常生长期，即在时间区间t∈T1:=(n，n+1-τ-τd]时，n=0，1，2，···，种群动力学由下面的模型刻画

在该系统中，D1和D2代表幼年个体和成年个体的扩散系数，出生率为关于成年种群密度的函数B(N2(t，x))，μ1和μ2代表幼年阶段和成年阶段的死亡率.其中，发育率M1(t，x;N2)需要通过详细考虑幼年个体在成熟期的空间移动以及死亡概率等因素.为此，引入t时刻在x∈Ω位置具有年龄a的种群密度p(t，x，a).假设τ为在此时间段上成熟的个体所需要的发育时间，则M1(t，x;N2)=p(t，x，τ).为了得到完整的模型，需要将p(t，x，τ)表述为关于变量I和M的泛函.此外根据对于年龄结构种群密度的McKendrick von-Foerster方程，在T1时间段上该变量可以由下面微分方程描述

由于p(t，x，τ)表示t时刻新发育的个体的密度，这些个体在t-τ时刻出生，故此可以在时间区间 [t-τ，t]上讨论变量p(t-τ，y，0)到p(t，x，τ)的演化:时间从t-τ时刻演化到t时刻，个体年龄从a=0发育为a=τ，此外由于个体可能的空间移动，在时间区间 [t-τ，t]上，个体位置可能由y变为x.引入新变量q(s，x):=p(t-τ+s，x，s).根据系统(21)的第一个方程，q(s，x)在年龄区间0＜s≤τ上的演化规则可以由下面方程给出

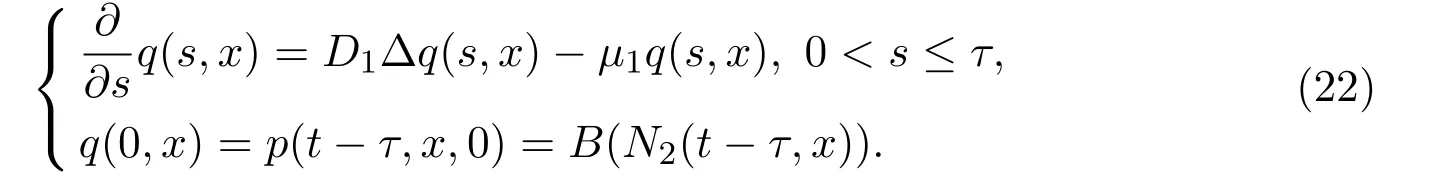
此演化方程描绘了幼年个体密度的动力学，考虑了个体的死亡和扩散过程.求解初值问题(22)(也可以由系统(21)的第一个方程用沿特征线积分法得出，如文献[57])可得

其中格林函数Γ(t，x，y)为由偏微分算子[∂t-Δ]在给定的边界条件下所定义的基本解.所以可得发育率

在滞育期T2:=(n+1-τ-τd，n+1-τ]时间段上，由于个体极端的低代谢活动，假设物种没有出生，发育以及空间移动.在此时间区间上，

此时，幼年和成年阶段的自然死亡率d1和d2一般大于T1和T3时间段上的对应的死亡率μ1和μ2.

当进入t∈T3:=(n+1-τ，n+1]时间段时，类似于方程组(20)，有如下方程

在该方程中，主要需要确立发育率M2(t，x;N2).由于T3时间区间长度为个体在正常环境条件下所需发育时间τ，所有在该时间段上新出生的个体不能在该时间区间完成发育.即所有新发育的个体必须在T1时间段出生，并经历滞育期T2.所以成熟个体经历的发育时间为τ+τd.此时，M2(t，x;N2)=p(t，x，τ+τd).类似于T1时间段上发育率的推导，可得个体密度从p(t-τ-τd，y，0)演化到p(t，x，τ+τd)的演化规律:时间从t-τ-τd时刻演化到t时刻，个体年龄从a=0发育为a=τ+τd，此外由于个体可能的空间移动，在时间区间[t-τ-τd，t]上，个体位置可能由y变为x.数学上可以描述如下

其中αt=n+1-t是依赖于t的时间刻度.此演化过程考虑了个体的移动和死亡.在坏环境季节(αt，αt+τd]∈T2时间段上，幼年个体不进行空间移动，只有自然死亡率d1.而在 (0，αt]∈T1以及 (αt+τd，τ+τd]∈T3上，幼年个体具有空间移动及自然死亡率μ1.求解该柯西初值问题可得

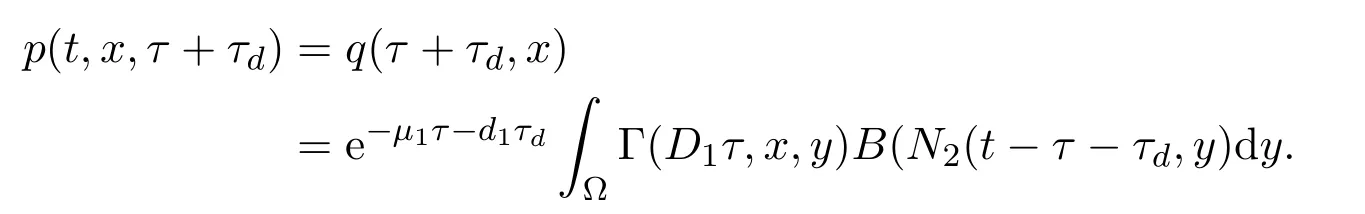
因此，该时间段上的发育率可以表述为

该发育率考虑了两个不同时间段的生存概率 e-μ1τ和 e-d1τd，其中在T1和T3时间段上的经历的时间为τ，在T2时间段上经历时长为τd.

综上所述，得出一个具有空间移动及不连续周期时滞的更替模型(20)，模型(23)以及模型(24).对于该模型，文献[56]考虑了有界区域及无界区域的情形.对于有界区域情形，定义了基本再生数，以及证明了系统的全局稳定性动力学.对于无界区域的情形，讨论了系统周期行波解的存在性以及渐近传播速度等问题.更多的建模过程以及分析细节可以参阅文献[56].

在本节最后，介绍具有空间移动的周期时滞系统相关研究进展.这些考虑个体空间移动的周期时滞模型研究极大地丰富了种群动力学相关结论，如具有阶段结构的蚊子种群生长反应扩散方程模型[58]，具有周期发育时滞的反应扩散阶段结构种群模型[59]，带有周期时滞以及考虑种内竞争的阶段结构反应扩散系统[60]，广义的具有周期时滞的时空媒介传播传染病模型[61]，具有周期时滞的反应扩散媒介传播疾病模型[55]，周期潜伏期的反应扩散多群组传染病模型[62]，具有非局部扩散及周期性潜伏期的蓝舌病传播模型[63]，周期性潜伏期及蚊子叮咬偏向性的疟疾传播反应扩散模型[64].此外，文献[65]考虑了在时间空间周期的环境中的种群扩散问题，文献[66]研究了季节更替对具有阶段结构种群扩散的影响，文献[67]讨论了带有周期时滞和非局部扩散周期系统所定义的庞加莱映射的扩散性态.

5 结论

本文主要展示了如何在一个阶段结构模型中引入周期发育时滞τ(t)，以及对于此类模型的分析思路.假设幼年个体在任何时刻具有正发育率，则该周期时滞可以通过累积发育率定义，此时，周期时滞为关于时间t的可微函数.但是当幼年个体由于受恶劣生存环境影响导致发育停滞(如物种进行滞育时)，则幼年阶段发育时滞为关于时间t的不连续函数.此类种群动力学可以由具有时滞的更替模型(succession model)描述.此外，这些更替模型可以从周期系统的观点进行研究.

本文中介绍的周期时滞主要用来描述从一个阶段到另外一个阶段的转化率(transit rate)，如从幼年到成年阶段的发育率，从潜伏阶段到感染阶段的转化率等.相较于更为具体的年龄结构或者尺度结构(size-structure)模型，阶段结构模型较好地平衡了生物复杂性与数学可分析性等方面的因素.期望此类研究能得到进一步的发展.

致谢 感谢白振国，李志民，罗颜涛和史洋洋对本文初稿提出宝贵意见!