导引头跟踪精度影响因素分析系统设计

程丹松，王 康，李晨博，杜敦伟，徐洲洋

（1 哈尔滨工业大学 计算机科学与技术学院，哈尔滨 150001；2 北京机电工程研究所，北京 100074）

0 引 言

导引头作为一种光电稳定跟踪装置，是精确制导武器的核心部件。在攻击目标过程中，弹体的角度和角速度通过导引头平台框架耦合到导引头探测器，直接影响导引头跟踪视线稳定和对目标跟踪性能。导引头跟踪视线角度精度与探测器在平台上安装精度、平台框架在弹体上的安装精度、平台框架角度初值、平台框架角速度、目标光点在导引头视线实现坐标系中的位置（目标运动特性）等因素有关，模型较复杂。本文针对直接稳像方案、间接稳像半捷联方案、间接稳像全捷联方案，建立安装误差和平台摆动角度／不同跟踪角偏差对跟踪视线角精度影响的关系模型，分析导引头跟踪视线精度的影响因素。通过仿真分析表明，转台性能和机械误差对仿真试验精度影响很小，而红外导引头轴向位置安装误差影响较明显。

1 惯性导航跟踪（导引头）控制原理分析

导引头视线的空域稳定技术，根据惯性传感器的布置位置，可以分为直接视线稳像和间接视线稳像两种方式。对此拟展开如下研究。

（1）直接视线稳像。直接视线稳像又叫机械稳像，是在机械上增加一套能够隔离载体方位、俯仰和滚动姿态变化的稳定平台，以实现视线的稳定。具体的方法是：利用装在控制对象上的速率陀螺，测量目标跟踪轴相对惯性空间的运动。这种情况下，目标跟踪轴相对惯性空间的运动起闭合伺服系统回路的作用。与间接稳像相比，直接稳像负荷较大，稳定精度高，适合在机载、弹载雷达上使用。直接视线稳像原理如图1所示。

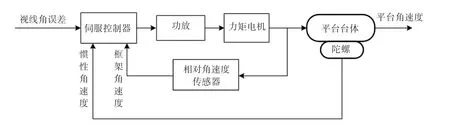
图1 直接视线稳像原理Fig.1 Principle of direct images stabilization

（2）间接视线稳像。间接视线稳像也称为数字稳定或捷联稳像。在间接稳像中，惯性器件不是安装在控制负载上，而是安装在负载的基座，然后在伺服控制器上采用数字稳定技术，修正或补偿载体姿态的变化影响，从而实现天线波束或瞄准线的稳定。具体方法是：利用载体惯性测量装置测量载体相对于惯性空间的运动，通过数字解算形成天线（相机）运动控制指令，抵消载体运动对实现的影响。这种情况下，目标跟踪轴相对载体的运动起闭合伺服系统回路的作用。这种稳定方法的特点是负荷较小，稳定精度较高。间接视线稳定原理如图2所示。

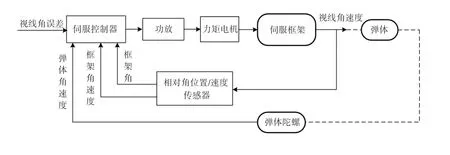
图2 间接视线稳像原理Fig.2 Principle of indirect images stabilization

研究可知，间接视线稳像一般有2种实现方式：半捷联方式和全捷联方式。两者都没有独立的闭环陀螺稳定回路。但半捷联方式具有框架结构，是在已有速度或位置回路的基础上，通过数字解算来补偿载体扰动；而全捷联方式则完全没有框架结构，是在电子角跟踪回路的基础上，利用数字解耦方式来实现视线稳定。

2 基于视觉测量模型的导引头视线角跟踪精度分析

本文在分析了直接稳像方案和间接稳像半捷联方案两轴稳定（包括滚动-俯仰式和航向-俯仰式）平台导引头跟踪控制原理；建立了地理坐标系（北天东坐标系）、弹体坐标系、体视线坐标系和视线坐标系之间的链式转换关系；并推导导引头跟踪视线精度模型，对跟踪视线角误差与安装角度误差和两框架角度的全微分展开，得到导引头跟踪视线精度与安装误差和两框架轴角度，以及框架角度测量误差之间的关系；推导两框架轴初始角度位置对跟踪视线角精度影响的表达式；开发仿真分析软件系统，在仿真分析软件系统上可视化展示各种安装偏差和两框架轴角度下目标光点在像面上的运动轨迹；通过设置大量实验用例表示两框架轴控制带宽对跟踪角度误差弯曲程度影响。

2.1 坐标系相互转换关系

捷联制导系统所应用的坐标系与各坐标系之间的转换关系如图3所示。

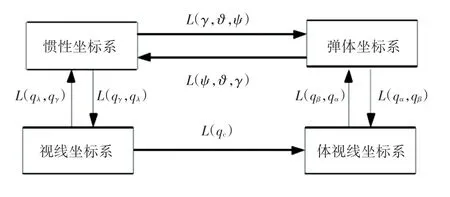
图3 各坐标系之间的关系Fig.3 Relationship between coordinate systems

（1）惯性坐标系与弹体坐标系之间的转换关系。由惯性坐标系到弹体坐标系的旋转关系矩阵为：

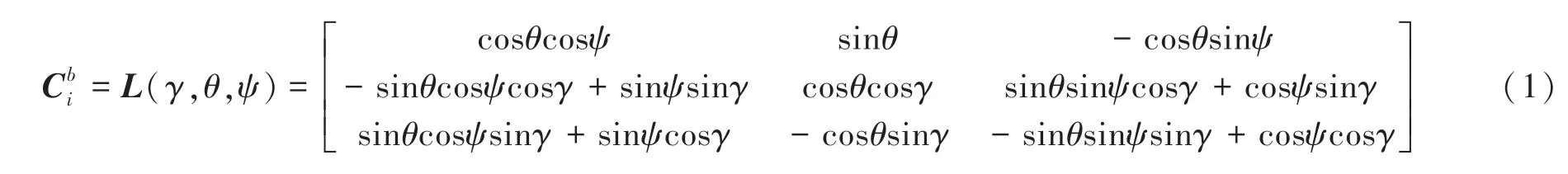
由弹体坐标系到惯性坐标系的旋转关系矩阵为：

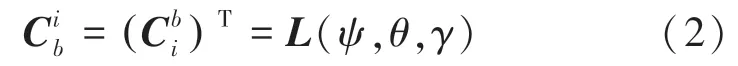
其中，为俯仰角；为偏航角；为滚转角。

且令：

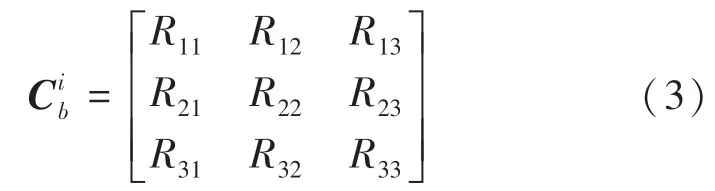
（2）惯性坐标系与视线坐标系之间的转换关系。两坐标系之间的旋转关系可通过视线方位角与视线俯仰角进行描述，其关系如图4（a）所示。

由视线角描述的惯性坐标系到视线坐标系的旋转关系矩阵为：

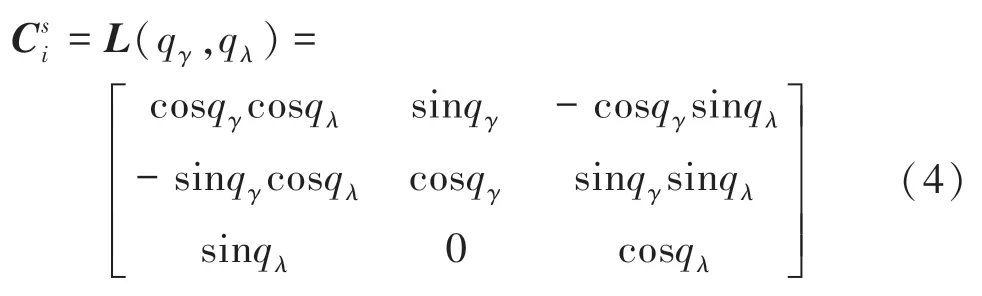
其中，q为视线方位角，q为视线俯仰角。

（3）弹体坐标系与体视线坐标系之间的转换关系。两坐标系之间的旋转关系可通过体视线方位角和体视线俯仰角来描述，其关系如图4（b）所示。

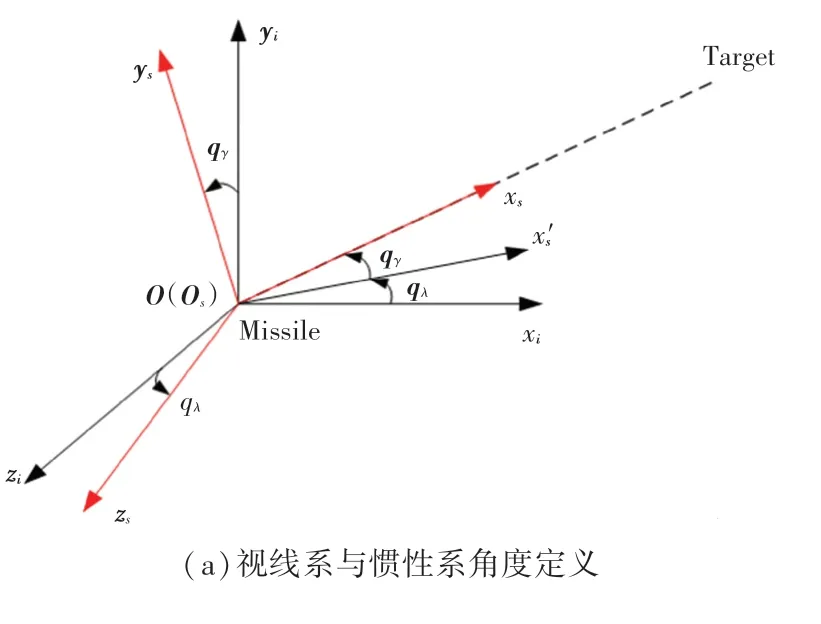
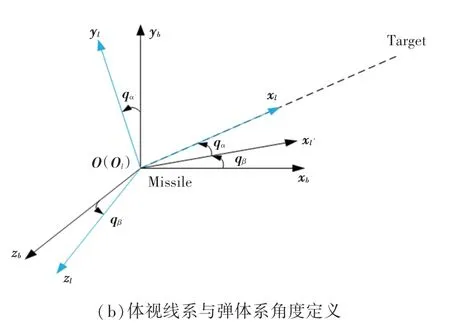
图4 坐标系与角度定义Fig.4 Coordinate system and angle definition

由体视线角描述的弹体坐标系到体视线坐标系的旋转关系矩阵为：

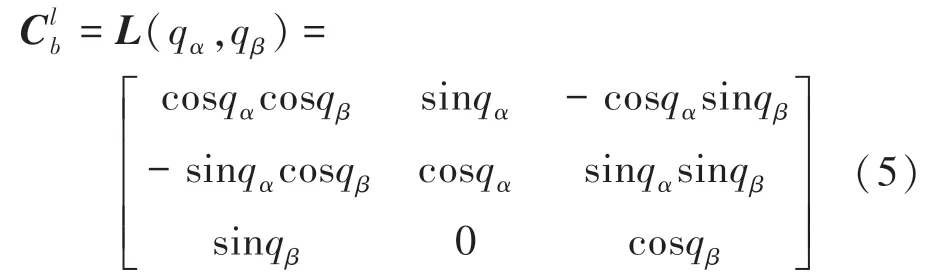
其中，q为体视线方位角，q为体视线俯仰角。

则有体坐标系与体视线坐标系之间的关系及其转换关系为：

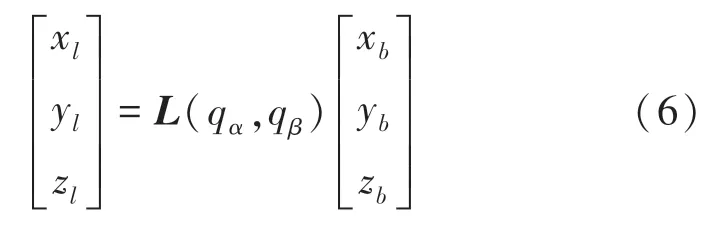
根据以上过程，同样的方法可以推得体视线坐标系转化为体坐标系的变换方程：

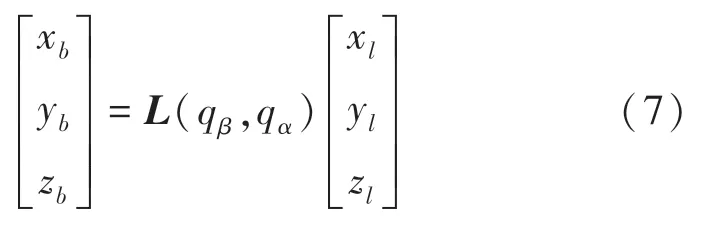
其中，

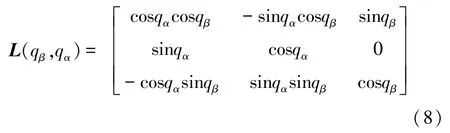
（4）视线坐标系与体视线坐标系之间的转换关系。由视线坐标系和体视线坐标系的定义可知：O轴和O轴重合且均指向全捷联导引头光学中心与目标连线方向。所以，这2个坐标系之间的转换关系一般用一个角度即可确定。定义视线变换角为视线坐标系的O轴和体视线坐标系的O轴之间的夹角。则由视线坐标系到体视线坐标系的旋转关系矩阵为：

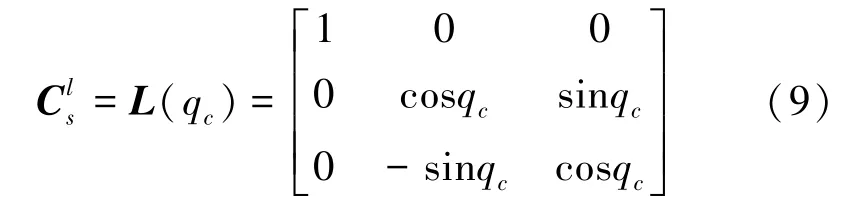
（5）地理坐标系与视线坐标系之间的关系及其转换，可表示为：

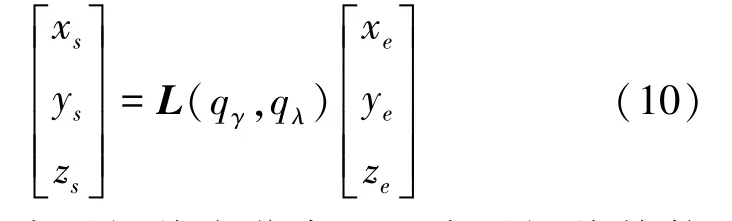
其中，q表示视线方位角，q表示视线俯仰角。（q，q）的数学表达式可写为：

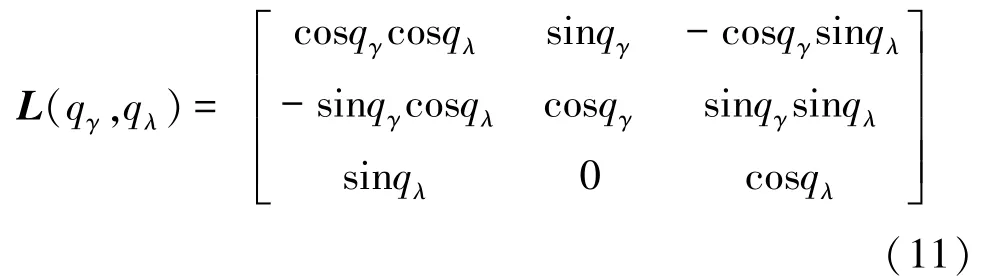
2.2 误差来源分析

在间接视线稳像惯导方式中，误差主要来源于以下几个方面：

（1）相机坐标系下探测器（相机）捕获到与目标之间的方位角q和俯仰角q存在误差。

（2）惯性坐标系下惯性器件测量得到的相对于惯性坐标系的偏航角θ、俯仰角φ、滚动角γ存在误差。

（3）载体坐标系下探测器（相机）的安装存在偏航角θ、俯仰角φ、滚动角γ的误差。

（4）载体坐标系下惯性器件的安装存在偏航角θ、俯仰角φ、滚动角γ的误差。

（5）惯性器件延时的测量结果带来的误差，比如测量结果有5 ms、10 ms的延迟等。

除了以上误差因素，针对直接视线稳像（平台式惯导方式）还存在平台坐标系相对于惯性坐标系的偏航角为θ、俯仰角为φ、滚动角为γ，所以根据以上误差因素，可以得到如下关系式：

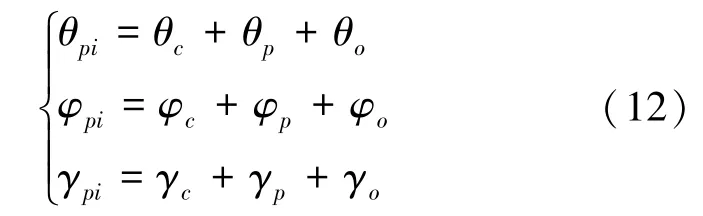
进一步地，假定载体坐标系与惯性坐标系均基于右手坐标系，且坐标系变换基于偏航-俯仰-滚动的顺序进行，则可以得到以下的数学关系式：

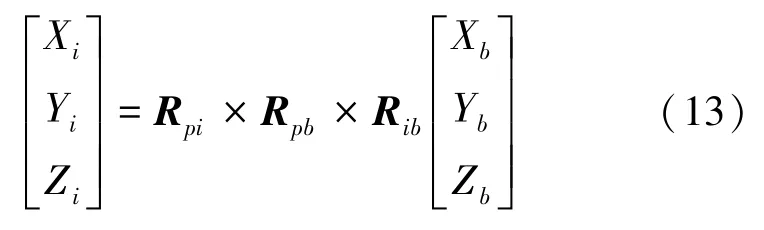
其中，（X，Y，Z）为目标在惯性坐标系下的方向向量，（X，Y，Z）为目标在载体坐标系下由探测器（相机）测得的方向向量。（X，Y，Z）可由探测器（相机）测得的与目标之间的方位角q与俯仰角q计算得到：

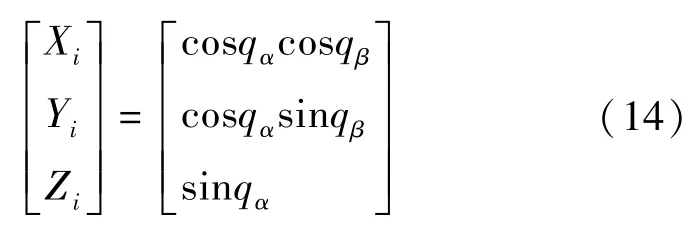
同时，R、R和R分别是载体坐标系到惯性坐标系的旋转矩阵、修正惯性器件安装误差的旋转矩阵和修正探测器（相机）安装误差的旋转矩阵。这3个旋转矩阵都可由如下公式计算得到：

由此可得到目标在惯性坐标系下的方向向量（X，Y，Z）和11个与误差有关的变量的关系式。接下来，可以由以下公式求得目标在惯性坐标系下的方位角q和俯仰角q：

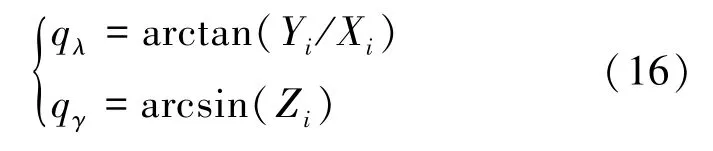
综合前文所述，对此内容的研究解析具体如下：

（1）针对间接视线稳像可以得到目标在惯性坐标系下的方位角q和俯仰角q关于11个和误差有关的变量的表达式，如下所示：

（2）针对直接视线稳像可以得到目标在惯性坐标系下的方位角q和俯仰角q关于14个和误差有关的变量的表达式，如下所示：

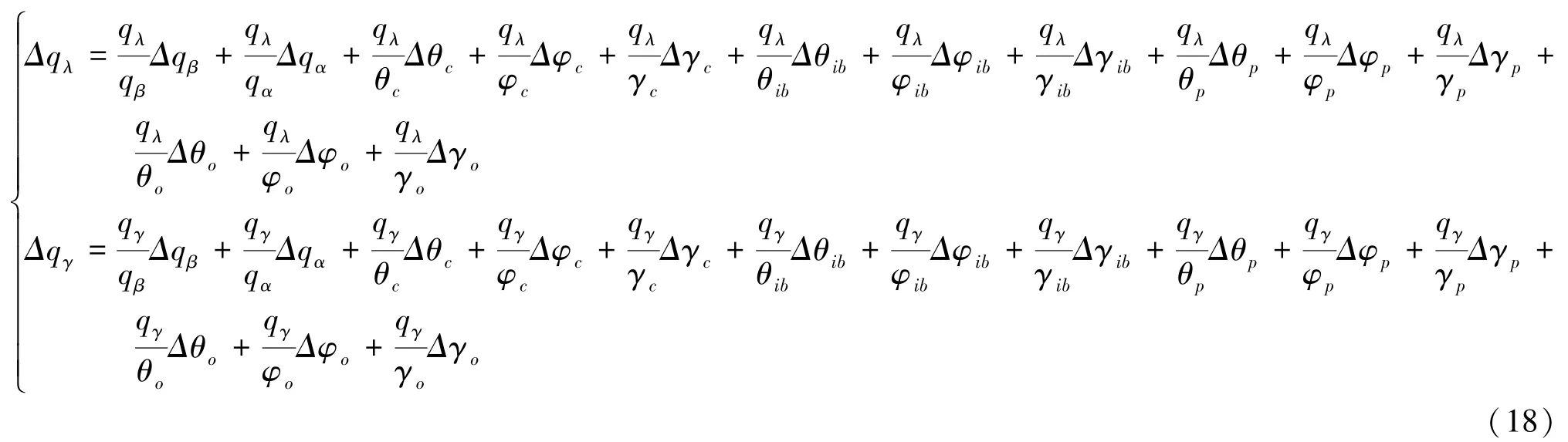
2.3 误差的计算过程

误差的具体计算通过Matlab的符号计算来实现，通过代入误差计算公式（17），会得到Δq和Δq关于11个变量的间接视线稳像平台全微分表达式；通过代入误差计算公式（18），会得到Δq和Δq关于14个变量的直接视线稳像平台全微分表达式，最后进一步进行数值计算。在这11个变量（或14个变量）中，假定探测器（相机）捕获到与目标之间的方位角q、俯仰角q和惯性器件测量得到的相对于惯性坐标系的偏航角θ、俯仰角φ、滚动角γ这5个变量是可以通过测量得到的，程序通过读取文件得到具体数值；剩下的6（或8）个变量分别是探测器（相机）与惯性器件的安装误差，假定都服从于均值为0、方差为1的正态分布，因此可以通过正态随机变量进行赋值，同时也可以通过将“误差控制”下的误差项设置为非零数来进行固定赋值。将全微分公式中的增量（每次变化量）默认初始化为0.001，这样q和q的全微分表达式就由符号表达式转化为数值表达式，直接计算即可。

程序将根据从文件中读取的信息进行计算，假定这些信息不包含误差，并且在计算过程中不考虑误差，将计算出来的结果作为真值并画出一条随时间变化的曲线；再考虑包含误差的情况，将程序随机生成的误差应用于计算过程中，又考虑测量延迟的影响，从而计算出另一条曲线作为实际测量结果，最后将2条曲线画在一幅图像里进行比较分析。

2.4 计算结果分析

本文研发设计的系统如图5所示。首先打开程序输入参数，可调整的参数为产生各种随机误差的参数、微分方程增量以及误差延迟，其余数据均可通过读取文本格式的文件得到。程序对所读取的文件的格式有一定的规范要求：每行有9个数据，可以有多行数据，类似一个二维矩阵，每列数据的含义为：载体坐标值、载体坐标值、载体坐标值、惯性器件偏航角、惯性器件俯仰角、惯性器件滚动角、目标坐标值、目标坐标值、目标坐标值。研究可知，这些数据均是相对世界坐标系下的测量值，角度的单位为度。

图5 程序界面Fig.5 Program interface

输入变量板块，可调整的参数为产生各种随机误差的参数（利用均值、方差数值产生正态随机数）、微分方程增量以及误差延迟，其余数据均由读取文本格式的文件得到。所标注的位置分别用来产生对应的随机偏差角度，点击重置误差按钮即可对所有误差角度值进行设定，也可手动输入修改。惯性器件延时误差默认设置为5 ms。

计算完成后程序会将结果保存到D盘，并将程序计算过程中出现的相位角误差最大时刻、垂直角误差最大时刻以及随机产生的误差的值显示在程序界面上。本系统针对捷联惯性系、半捷联惯性系和平台惯性系三种情况进行仿真，每种情况包含2幅生成的图像和一些具体计算结果文件，这2幅图像分别为：惯性系垂直角及其相关计算值（包含惯性系俯仰角、惯性系俯仰角全微分值、惯性系俯仰角全微分值偏导数）和惯性系相位角及其相关计算值（包含惯性系相位角、惯性系相位角全微分值、惯性系相位角全微分值偏导数）。相应处理结果如图6～图11所示。

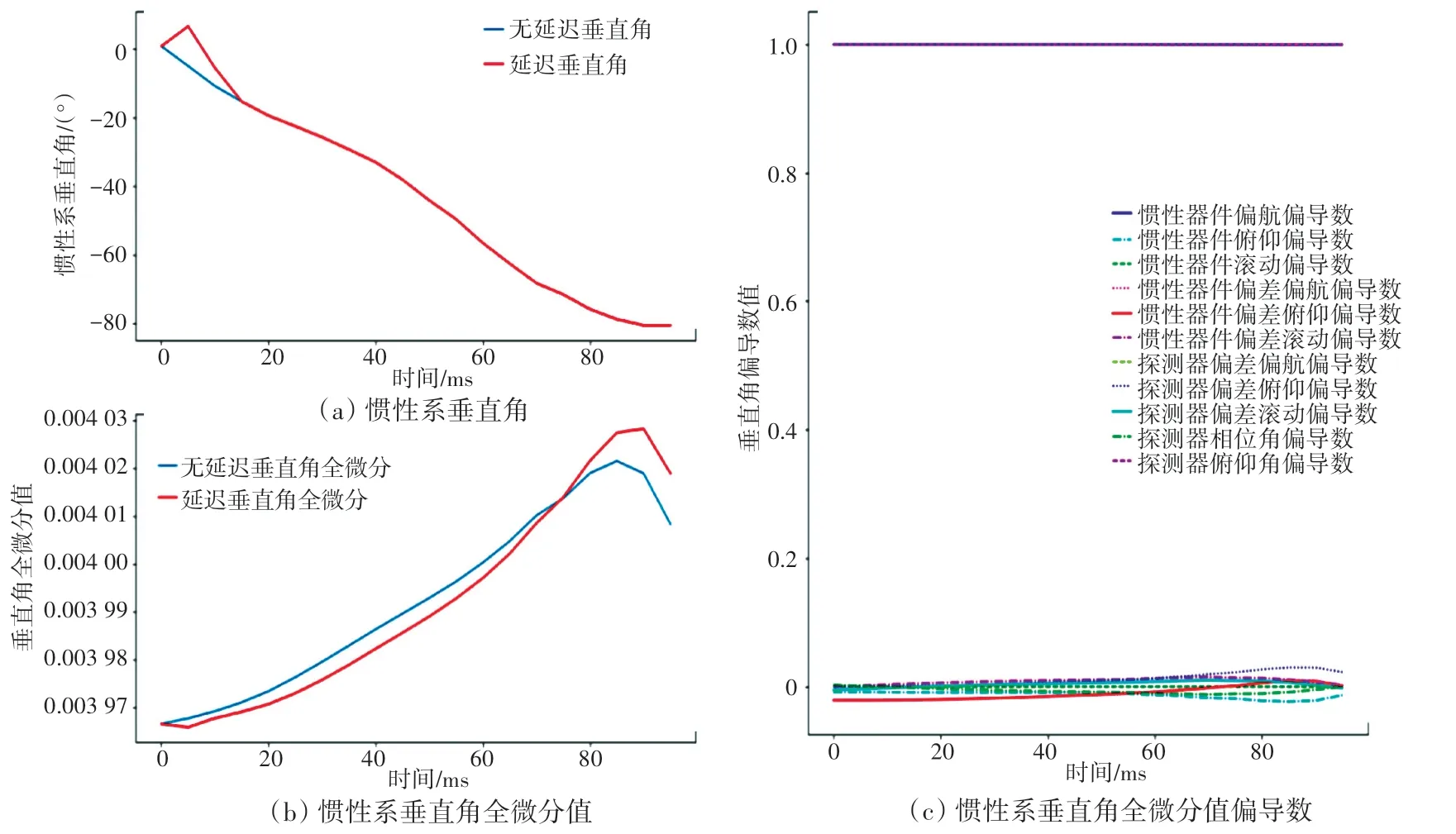
图6 捷联惯性系垂直角及其相关计算值Fig.6 Vertical angle of Strapdown Inertial Navigation System and its related calculated values

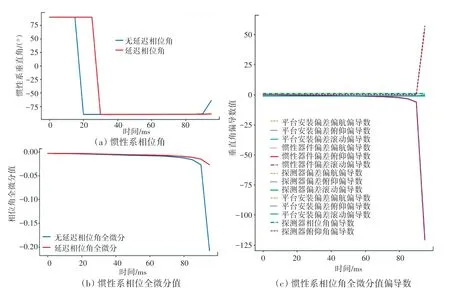
图11 平台惯性系相位及其相关计算值Fig.11 Phase angle of platform inertial system and its related calculated values

图7 捷联惯性系相位及其相关计算值Fig.7 Phase angle of Strapdown Inertial Navigation System and its related calculated values

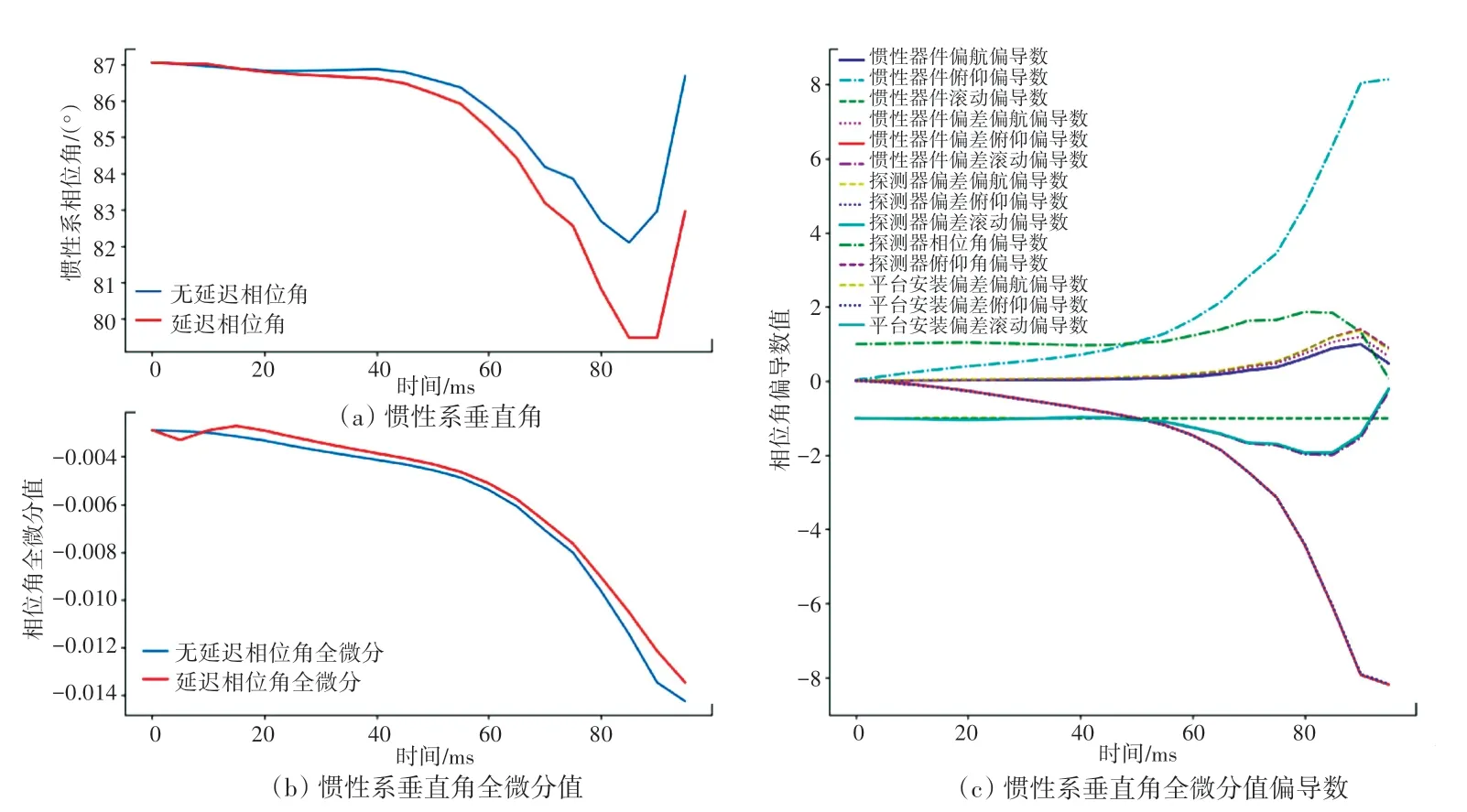
图8 半捷联惯性系垂直角及其相关计算值Fig.8 Vertical angle of Semi-strapdown Inertial Navigation System and its related calculated values

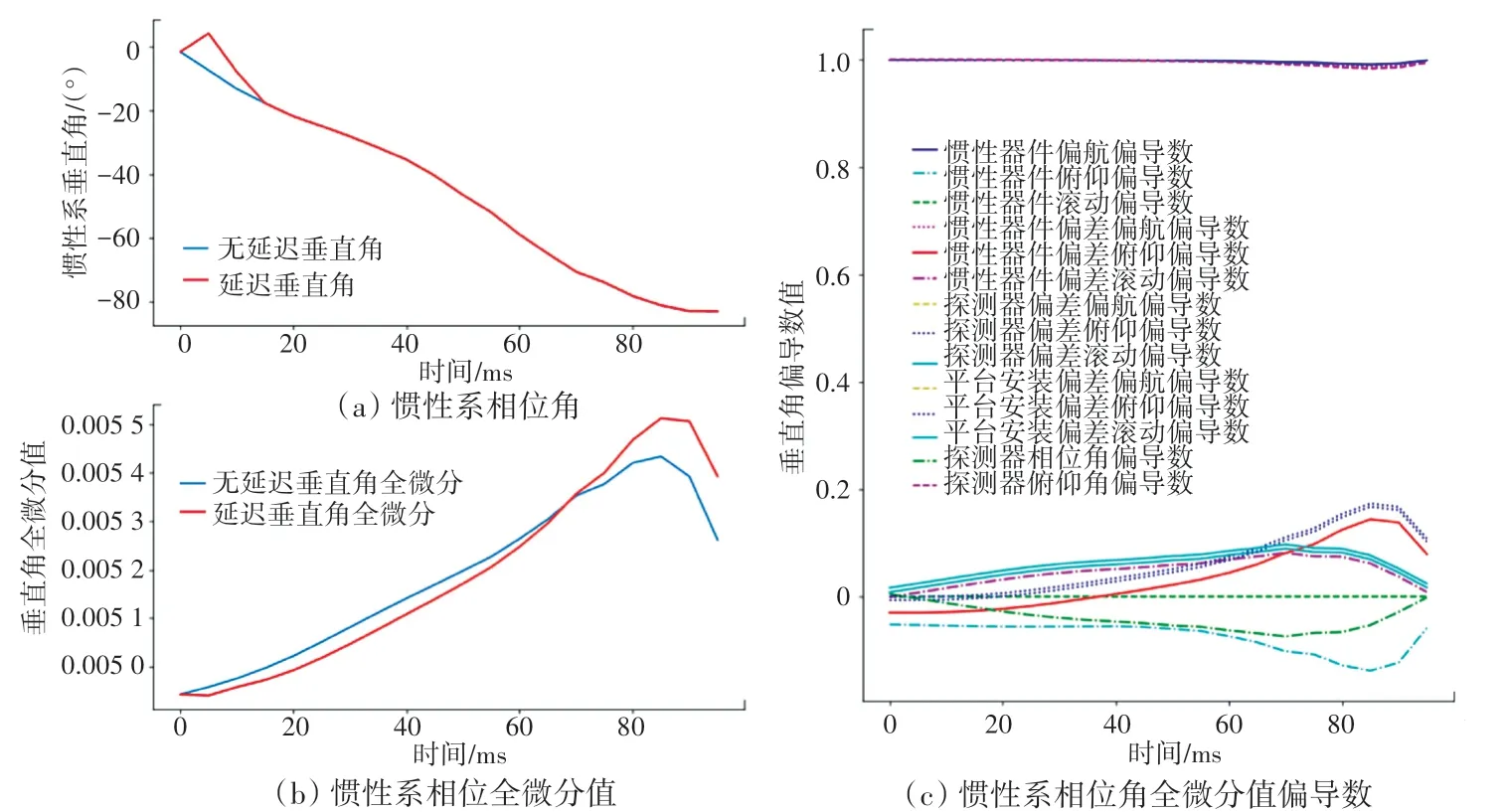
图9 半捷联惯性系相位及其相关计算值Fig.9 Phase angle of Semi-strapdown Inertial Navigation System and its related calculated values

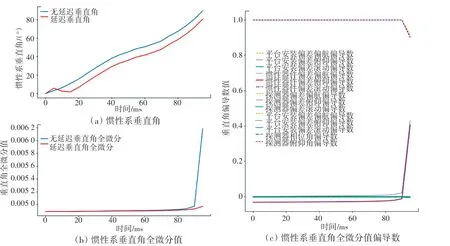
图10 平台惯性系垂直角及其相关计算值Fig.10 Vertical angle of platform inertial system and its related calculated values

分析图6～图11后可以得出以下结论：导引头安装误差包括轴向、高低、侧向位置垂直、轴向安装角误差。导引头高低、侧向位置安装误差和安装角误差是由夹具、转台、导引头上各安装面的形位公差和配合关系决定，一般误差量值很小。通过仿真试验也表明：针对单误差，以及水平、平面控制导引头，导引头高低、侧向安装位置误差和垂直、轴向安装角误差对试验过程和结果的影响很小。相对于水平安装角误差，导引头轴向位置误差对试验过程和结果影响比较显著，导引头测得的目标方位误差随安装误差的增加而显著增大，一定程度上影响了导弹命中与否的判断。

3 结束语

由仿真结果可以确定，惯性器件的偏差对姿态、速度和位置解算结果均有影响，并且随着恒偏差的增大，误差成近似比例增加。其中在惯性系相位角方面，惯性器安装误差俯仰角偏导数、惯性器俯仰角偏导数和探测器安装误差俯仰角偏导数对整个误差的影响最大。在惯性系俯仰角方面，惯性器安装误差偏航角偏导数和惯性器俯仰角偏导数对整个误差的影响最大。对应的补偿手段可以采用滤波去噪方法或者极限位置规避。