基于STM32的主动激励式触觉传感器滤波算法对比

刘聂天和，王民慧，黄佳鑫

（贵州大学 电气工程学院，贵阳 550025）

0 引 言

触觉传感器及触觉传感技术一直以来都是机器人在对物体进行感知与探索工作的重要部分。从上个世纪开始，人们开始研究触觉传感技术，但研究内容仅限于传感器与被测对象之间的接触性与接触力度。随着传感技术的发展，越来越多的专家学者开始对机器人触觉传感器进行研究。

Nicholls等人在综述中曾经指出，从上世纪70年代开始，国外已经开始对机器人及触觉传感技术展开研究。因当时只是检测是否接触到被测物和接触力度的大小，研发出来的传感器相对较为简陋，功能比较单一。到了上世纪80、90年代，触觉传感器处于高速发展阶段。进入这个阶段后，越来越多的专家学者针对传感器进行了更加全面的研究。从基本原理出发，使用了先进的材料、精度更高的传感器并简化了使用方法。在此期间，触觉传感器多是基于电容式、电阻式、压电式等工作原理，多用于测量物体表面形状、压力分布等参数，但对于纹理、硬度等参数测量却还无法实现。

随着新世纪的到来，触觉传感器原始材料和生产工艺得到了快速发展，这就意味着传感器从各个方面都得到了很大的提升，开始向柔性化、多阵列、高灵敏度等方向发展，而且研究热点通常集中在电子触觉皮肤等柔性触觉传感器方面。到目前为止，触觉传感器只适用于高精度且环境柔和的工作场所，并不适用于恶劣粗糙的环境。因此，本文提出的主动激励式触觉在线识别系统，为该方向研究提供了一种新的思路。

国内触觉传感器的研究相对国外稍晚一些，上世纪80年代有关触觉传感器的研究即已引起国内学者关注。其中，东南大学机器人传感与控制技术研究所、哈尔滨工业大学、杭州电子科技大学、北京理工大学、中科院沈阳自动化所等科研单位皆已陆续推出有关触觉传感器的系列研究成果。1987年在中国制定的863计划中，将阵列触觉传感器作为重点进行立项，同时在此计划的支持下，触觉传感器在90年代也得到了飞速发展。21世纪开始，中国在触觉传感器方面的发展进入了快车道，众多研究单位随即创立，但一般情况下致力研究的触觉传感器仍然局限在基于柔性化、阵列化和轻量化的电子触觉皮肤等方面，对于应用在粗糙恶劣环境等方面的触觉传感器研究尚有不足，同时国内到目前为止对于主动激励触觉传感器方面的研究也仍处于试验阶段，并不具有实时性。现阶段对于触觉传感器识别算法的研究一般是通过机器学习或者卷积神经网络等技术，对采集到的数据进行处理，但这些触觉感知技术大多应用于机器人皮肤嵌入式阵列单元等方面，对于本文研究的主动激励触觉传感器应用仍然较少。本文拟对此展开研究论述如下。

1 系统方案设计

本设计主要由传感器模块、控制器模块和数据采集模块等构成。该系统以STM32F407ZGT6单片机作为主控核心控制器，通过传感器模块对不同状态传感器数据信息进行采集，而后传给STM32F407ZGT6单片机；数据处理转换后，在电脑上用Matlab进行可视化绘图。系统总体结构如图1所示。

图1 系统总体结构图Fig.1 System overall design drawing

本设计以STM32F407ZGT6单片机作为主控核心控制器。一方面，利用压电陶瓷传感器模块采集不同状态传感器数据，随后将数据传输到STM32F407ZGT6单片机中，再通过串口通信方式将单片机上的数据传输到串口调试助手中。另一方面，通过串口调试助手接收到数据后加以保存，并在Matlab上进行数据可视化。

2 数据预处理研究

2.1 一阶滤波

一阶滤波、也称为一阶惯性滤波或一阶低通滤波，常常可以通过模拟电路或者通过软件两种方式实现。这里将给出分析阐释如下。

（1）模拟电路。模拟电路方式通常使用电阻和电容共同搭建的硬件RC低通滤波，常见用于交流信号、直流信号和脉冲信号等方面。典型电路如图2所示。

图2 一阶滤波典型电路图Fig.2 Typical circuit diagram of first-order filtering

根据基尔霍夫电压定律可以得出：

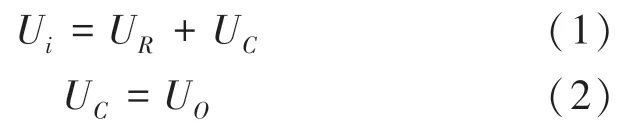
电路中电流可以通过流经电容的电流得出：

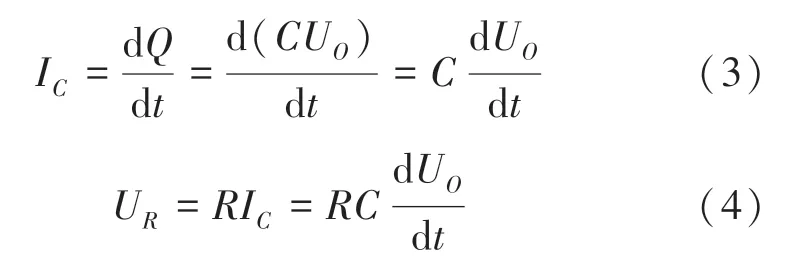
最后通过上述公式推导得出一阶微分方程为：

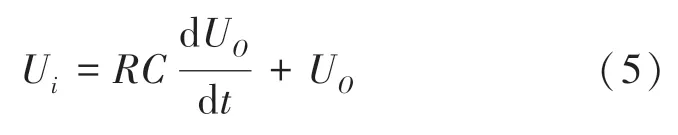
通过求解得到输出与输入关系为：

（2）软件方式。一阶滤波的实现，一般通过最新采样值与前一次经过滤波后的采样值进行加权，得到最新滤波值。使得滤波过程中，上一次输出对下一次输入有反馈作用。这里，研究推得的一阶滤波算法公式为：

其中，为滤波系数，一般取值为01之间；表示最新采样值；为前一次经过一阶滤波得到的输出结果；表示最新采样值与前一次经过滤波后的采样值进行加权得到最新输出结果。

程序设计流程如图3所示。图3中，为滤波系数，一般取值为0～1之间；表示待处理的数据量；表示最新采样值；表示前一次经过一阶滤波得到的输出结果；表示最新采样值与前一次经过滤波后的采样值进行加权后的最新输出结果；表示滤波后的全新数组。

图3 一阶滤波流程Fig.3 First-order filtering flow chart

2.2 中值滤波

中值滤波、也叫中位值滤波，是当下常见的有效过滤噪声的一种非线性平滑技术。中值滤波在滤除噪声的同时，还能保护信号的边缘。此处的中值或者中位值是指选定数据区域，并按照从小到大、或者从大到小的顺序进行排列。若选择数据总数为奇数时，则选取中间数值作为中值或者中位值；若选择数据总数为偶数时，则选取中间2个数据的平均值作为中值或者中位值，对此可表示为：

中值滤波流程如图4所示。

图4 中值滤波处理流程图Fig.4 Flow chart of median filtering processing

在做中值滤波时，采用冒泡排序法对需要滤波的数据从小到大进行排列。其中，表示定义滤波数据第一个数值为0，随后从开始保存每次采样数值，与前一个数值进行比较；表示选择一次中值滤波所需要的数据个数。

2.3 五点三次平滑处理

五点三次平滑处理算法，是一种利用最小二乘法在等间距数值的基础上，对数据进行三次最小二乘多项式平滑的处理算法，通常用来处理带有毛刺或者噪声的数据。此处需用到的数学公式为：

一般情况下，设序列x（1，2，…，），推演得到的五点三次平滑处理计算公式为：

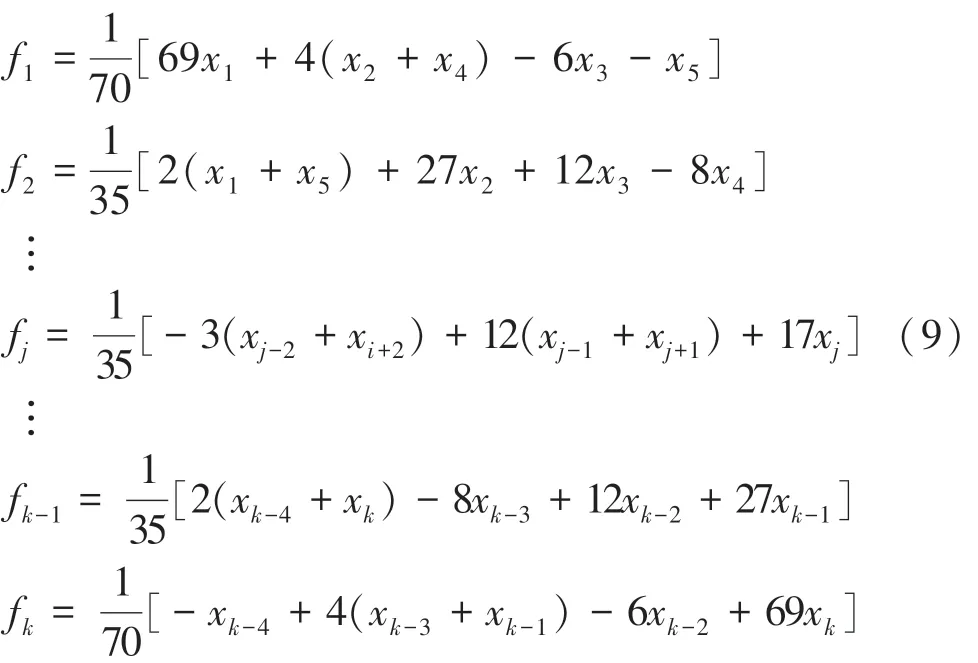
其中，f是x经过五点三次平滑处理后的输出（3，4，…，2），为每次滤波的数据个数。具体流程如图5所示。

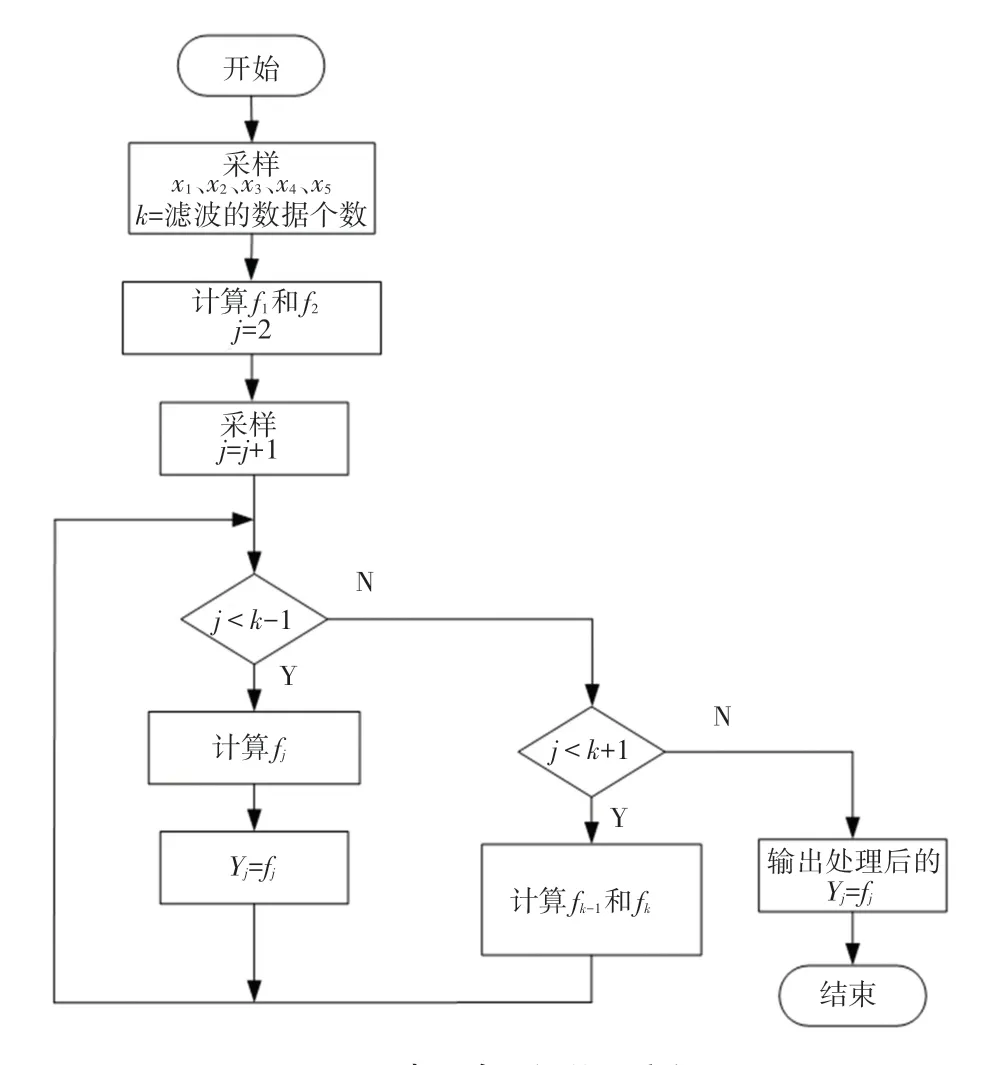
图5 五点三次平滑处理流程图Fig.5 Flow chart of five-point cubic smoothing

2.4 滤波效果对比

本课题使用的是基于三级钢板压电陶瓷作为传感器，在数据采集过程中不可避免会产生噪音信号或者干扰信号。因此，在做数据分类前就要进行数据预处理，滤掉噪点，方便后期分类处理。根据上述分析可知，一阶滤波具有稳定、易操作等优点；中值滤波在滤除噪声的同时，还能保护信号的边缘；五点三次平滑技术在数字信号处理中有着广泛应用，算法稳定性较高。本文利用3种方式进行数据预处理，并将处理效果进行比较。处理结果如图6所示。

图6 滤波算法对比Fig.6 Comparison of filtering algorithms

从效果图可以看出，原始数据存在很多噪点，经过一阶滤波后噪点有所缓解，但是还存在很多噪点，而中值滤波效果相对五点三次平滑处理和一阶滤波好很多，保留了信号原始的轮廓，同时也对噪点做了很好的处理。

本文选取效果最好的中值滤波算法，将程序移植到单片机上进行复现，应用于机械手中进行去噪。将原始信号、单片机滤波信号、Matlab滤波信号对比后发现：单片机上的中值滤波较好地还原了Matlab上中值滤波的效果，二者差值较小。具体处理效果如图7所示。

图7 单片机与Matlab滤波效果对比Fig.7 Comparison of microcontroller and Matlab filtering effect

3 结束语

本文在对比了一阶滤波、中值滤波和五点三次平滑的预处理效果后，选择了效果最好的中值滤波进行数据处理，最终应用于STM32F407ZGT6单片机上，并对比Matlab的实验运行结果，验证其具有较好的滤波效果。