基于BM3D去噪算法在天文图像中的应用
2022-09-28唐艳,潘伟,张利,许丽,覃芹
唐 艳,潘 伟,张 利,许 丽,覃 芹
(1 西华师范大学 计算机学院,四川 南充 637009;2 贵州大学 大数据与信息工程学院,贵阳 550025)
0 引 言
天文图像能够直接获取天文信息,对于探索和理解宇宙有着至关重要作用。由于宇宙环境的影响以及地面接收传输过程中的射频干扰,导致天文图像成像过程中存在噪声,影响图像观测效果。天文图像是天文学家观测宇宙的重要一手资料,噪声带来的干扰点会影响图像的形状,严重的会淹没图像的特征、无法确定观测目标,导致难以进行观测,得出错误的结论。
宇宙天体发射各种可见和不可见光波波段。1991年,基于干涉阵列的原理,平方公里阵列首次被提出。1993年,在国际无线电科联会议上,10个国家联合提议共同建造平方公里阵列射电望远镜(SKA)。SKA是世界上最大的射电望远镜,由世界上十多个国家一起修建、运营、维护和管理。低频SKA、即SKA1-low是其第一个课题:宇宙再电离研究。SKA1-low采用低频波获取难以发现的微弱的中性氢辐射信号,探测宇宙中的第一缕曙光。2018~2023年是SKA1的建设阶段,预期在2024年开始观测,SKA1-low是全世界唯一一个可实现宇宙再电离成像观测的射电望远镜。由于接受信号不可避免地带有噪声,因此SKA1-low对中性氢辐射信号观测得到的图像必须经过去噪处理。
早在90年代初,天文研究人员就将图像去噪应用于天文领域,最初是大量利用小波分析进行研究,随即提出了局部高斯去噪;小波去噪方法也在早期得到大量的应用,研究者利用小波成功地排除了观测到的射电图中的干扰线,该方法在去噪过程中能够尽可能多地保留有用信息。随后又对小波去噪进行了大量的优化研究,Nurbaeva等人使用合成数据对3种不同的去噪技术:中值滤波、维纳滤波和离散小波变换(DWT),进行了测试,提出了一种将小波变换与维纳滤波相结合的去噪方法,提高了测量的质量因子,最好达到2倍。2005年,Buades等人提出非局部均值检测(Nonlocal means,NLM)算法,利用图像的非局部相似性来消除图像中的噪声,但由于其复杂程度过高,导致去噪效率低下,不能很好地去除噪声大的图像的噪声。Zhang提出了一种改进的CLEAN算法,利用尺度基函数将天文图像参数化,以表达像素之间的相关性,从而进一步消除图像残差,恢复图像细节。Dabov等人提出的三维块匹配算法(block-matching and 3D filtering,BM3D),利用空间域寻找相似图像,利用频率域来分析图像内及图像间的变化关系,提升了图像在变换域的稀疏表示,更好地保留图像的细节信息,是当前降噪性能最好的通用图像降噪算法之一。本文将BM3D算法应用于SKA1-low天文图像去噪,经对比实验证明,BM3D应用于天文图像的去噪上有明显效果。
1 BM3D去噪算法
1.1 BM3D算法背景
非局部均值滤波(non-local means,NLM)算法,利用噪声图像中存在的冗余信息来消除噪声,将图像割裂成许多的图像块,再进行相似图像块搜索,区域间的相似度可以用欧拉距离来衡量。
BM3D算法对NLM算法进行融合优化,吸收NLM算法中的非局部块匹配方法。利用局部块匹配方法,使用参照图像块对整幅图像进行搜索,找出相似的块;对于相似度的计算,BM3D不再使用欧氏距离,而是采用阈值对比的方法计算图像块的相似度,将比阈值小的灰度值清零合并,大大减少了图像块之间相似度的计算量,实现了阈值线性变换。在对相似块进行搜索后,NLM只是简单地进行加权平均,去除图像中的噪声,但是BM3D结合小波变换域的方法,对相似的图像块使用协同滤波处理,能够减少相似块之间的噪声,再进行相似块的域转换,在聚合过程中又做了加权处理,最后构造去噪后的图像块。既吸收了NLM相似块匹配的思路,又融合小波变换域去噪的方法,BM3D算法去噪对于天文图像的去噪具有借鉴和应用意义。
1.2 BM3D算法原理
BM3D算法是目前最好的去噪算法之一。该算法采用NLM的非局部块匹配的方法,把相似的图像块堆叠成三维图像。算法分为基础估计和最终估计两步。其中,基础估计通过加权平均去除大量的噪声;而最终估计则是恢复图像的细节特征。BM3D算法原理如图1所示,每一步包含:相似块分组(Grouping)、协同滤波(Collaborative Filtering)和聚合(Aggregation)。
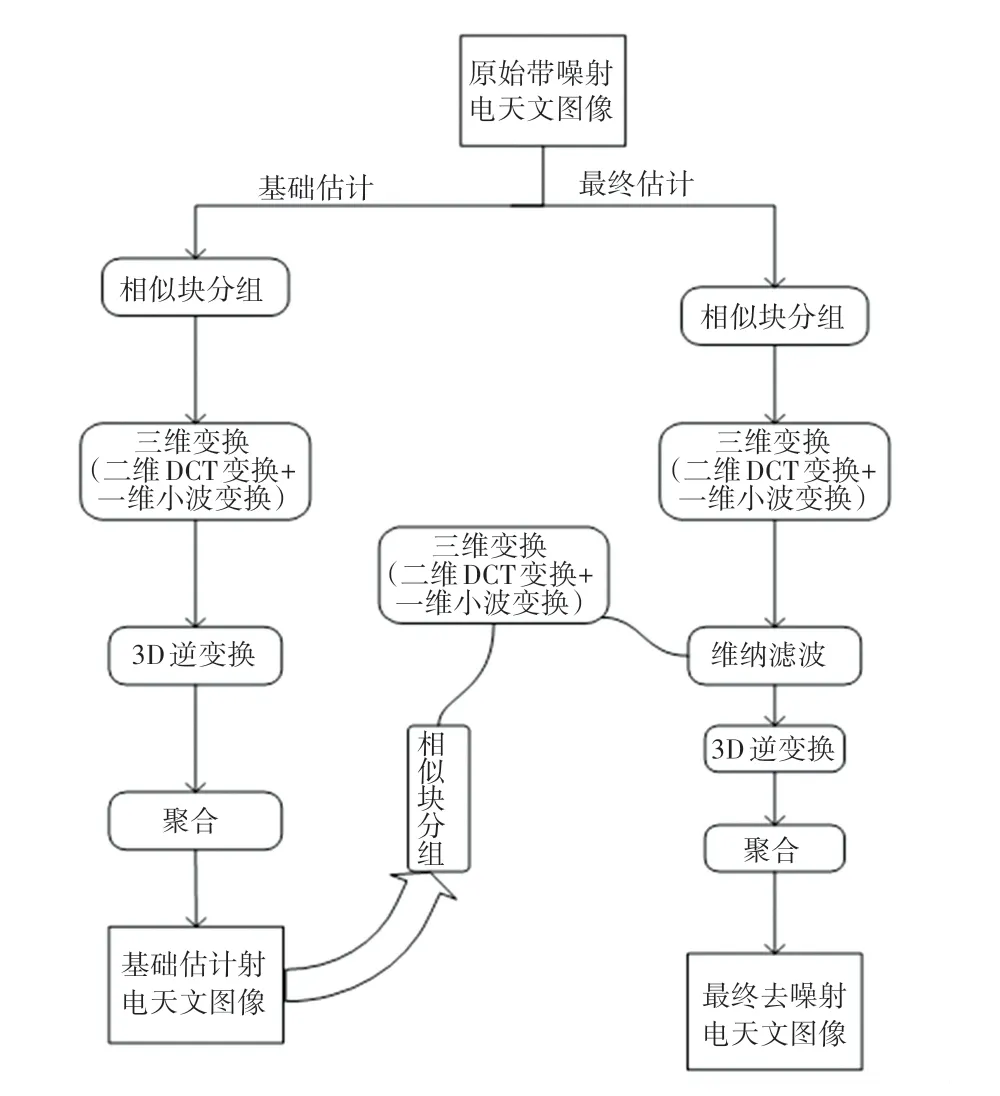
图1 BM3D算法原理Fig.1 Schematic diagram of BM3D algorithm
1.2.1 基础估计
(1)相似块分组。构造的目标块(实验选取8),在适当范围的窗口(实验选取为39×39)上按照滑动步长为3来搜索图像块,对于每一个选取的目标块,在其附近寻找16个相似的像素块,并将其和目标块堆叠到一个三维矩阵中去,将其差异度设置为0,相似块的距离为欧式距离,可以表示为:
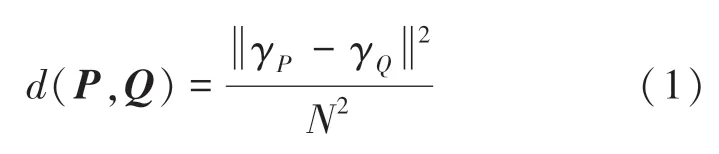
其中,γ和γ为图像块对应的矩阵数值。
相似块的距离要大于0,小于相似块之间的阈值τ(实验选取τ=2 500),其值可由如下公式计算求出:
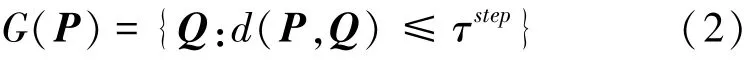
其中,(,)为2个矩阵的欧氏距离。
(2)协同滤波。首先对矩阵进行变换,找出三维矩阵中的二维块,做二维余弦变换(DCT变换);取出矩阵的第三维做阿达马变换(Hadamard Transform)。经过上述变换,会存在小于参数(实验设置=27)的成分,使用硬阈值的方式将这些成分设置为0。计算不为0的数量作为权重参考,最后进行反变换,推导得出的数学公式可写为:

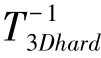
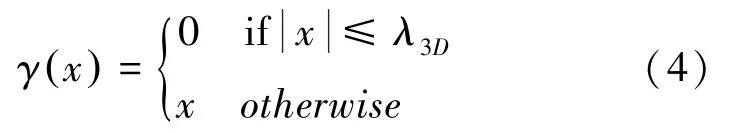
其中,=27。
(3)聚合。每个图像块都是去噪估计。将其进行逆变换后交融到原本的位置,对每一个估计加权求平均,权重的大小由硬阈值设置为0的总数以及图像噪声的强度决定。处理后的图像已经去除了大量的噪声,仅存较少的噪声点。
1.2.2 最终估计
与基础估计去除噪声不同,最终估计的目的是恢复图像的细节特征。在基础估计后,结合原来的噪声图像,采用协调滤波来恢复图像的细节特征。对此拟做阐释分述如下。
(1)相似块分组。采用基础估计图块的欧氏距离(,),将搜索窗口大小改为25×25,将距离最小的32个图块,组成三维矩阵。最终估计会结合原本的噪声图像,因此会形成2个三维矩阵。一个是原本的噪声图像的三维矩阵,另一个就是经过基础估计处理之后的图像的三维矩阵。
(2)协同滤波。使用3D维纳滤波(3D Wiener Filtering),通过噪声强度以及基础估计矩阵的值,对噪声图像的矩阵系数进行缩放,数学表述具体如下:
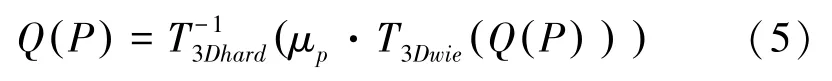
其中,μ是维纳滤波的系数。
(3)聚合。加权的权重取决于协调滤波中的维纳滤波系数和噪声强度。
对比基础估计,最终估计还原了更多原图的细节。因此BM3D算法将大量的运算放在相似块分组的计算上,同样大小的相似块搜索,BM3D算法的复杂度大概是NLM的3倍。
2 实验与分析
2.1 实验环境
本次实验运行环境见表1。由于宇宙噪声属于高斯噪声,本文考虑引入的噪声信号为高斯白噪声。选取一张模拟的SKA1-low天文图像,在该图像上混入不同的高斯噪声来模拟成像过程中会产生的噪声;分别采用NLM算法以及BM3D算法进行去噪实验。

表1 实验运行环境设置Tab.1 Experimental settings
2.2 实验数据集
本实验是基于SKA1-low的射电天文图像的去噪研究,由于SKA目前正在建设中,因此实验所使用的数据集是通过不同的射电源,经过SKA-low的配置模拟得到的,实验模拟SKA成像过程中产生噪声的干扰因素,如热噪声干扰、地面接收射频干扰、电离层干扰等,对模拟出来的数据集添加噪声。
2.3 实验效果对比
研究模拟出来的SKA1-low图像如图2所示,添加标准差分别为10、25、50的高斯噪声,结果如图3所示。对噪声图像分别采用中值滤波、NLM算法以及BM3D算法去噪,选取25的噪声图像去噪之后的结果进行对比,如图4所示。图4中,红色方框为局部细节放大,经过中值滤波后的图像噪声点依旧明显,去噪效果并不理想,NLM算法去噪图像相对较好,BM3D算法去噪后图像效果最好。

图2 SKA1-low图Fig.2 SKA1-low figure

图3 不同高斯噪声图Fig.3 Different Gaussian noise graphs

图4 高斯噪声去噪效果对比图Fig.4 Comparison of denoising effect of Gaussian noises
2.4 实验结果分析
2.4.1 评价指标
实验选择峰值信噪比()、结构相似度()和特征相似度()作为评价图像质量的评价指标,其值越大表示去噪效果越好,图像的恢复也就越好。对此可展开研究论述如下。
(1)。数学定义如式(6)所示:
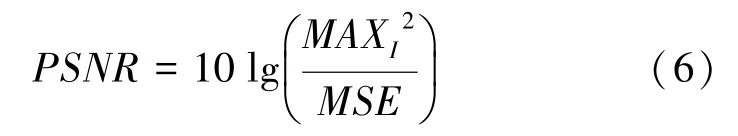
其中,MAX表示图像点颜色的最大值。本实验中采样点为8位,则MAX=255。
(2)。为损失函数,数学定义如式(7)所示:
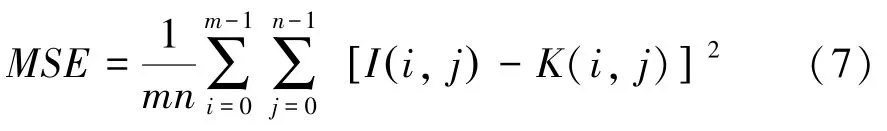
其中,和分别为的单色图像。
(3)。是衡量2张图片相似度的指标。与不同,是感知模型,更加符合人眼的直接观测结果,的取值范围为[0,1]。当2张图片完全相同时,1。的数学定义如式(8)所示:

其中,μ和μ表示2个图像的像素平均值;σ和σ表示2个图像的像素标准差;σ表示2个图像的像素协方差。
(4)。将一张图片的像素根据其重要性不同添加不同的权重,再利用特征相似性来评价图片质量。的数学定义如式(9)所示:
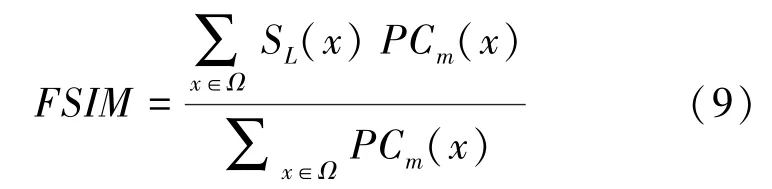
其中,表示图像的相位一致性(phase congruency,),其数学表达式可写为:
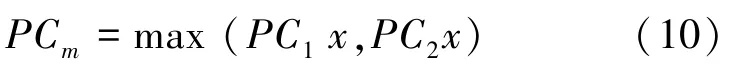
S表示和(梯度特征相似度)的融合度,其数学表达式可写为:

其中,S表示为梯度特征相似度()。
2.4.2 实验结果
使用、和对中值滤波、NLM算法以及BM3D算法进行评价。
本次实验中,不同模型对图像去噪的,见表2,BM3D算法去噪后的更好,其均值达到41.180 9 dB。不同模型对图像去噪的,见表3,BM3D算法去噪后的图像更好。恢复图像结构更好。不同模型对图像去噪的,见表4,BM3D算法的图像特征还原均达到0.9以上,更好地还原了图像的特征。
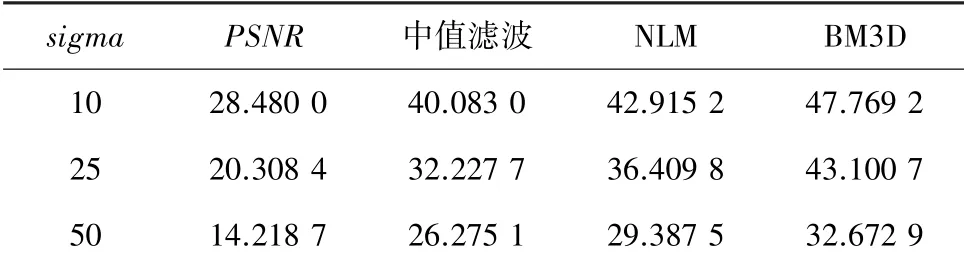
表2 不同模型对图像去噪的PSNR对比Tab.2 PSNR comparison of images denoising by different models
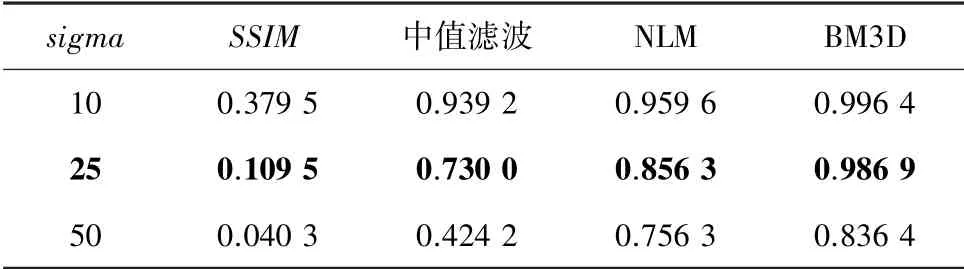
表3 不同模型对图像去噪的SSIM对比Tab.3 SSIM comparison of images denoising by different models
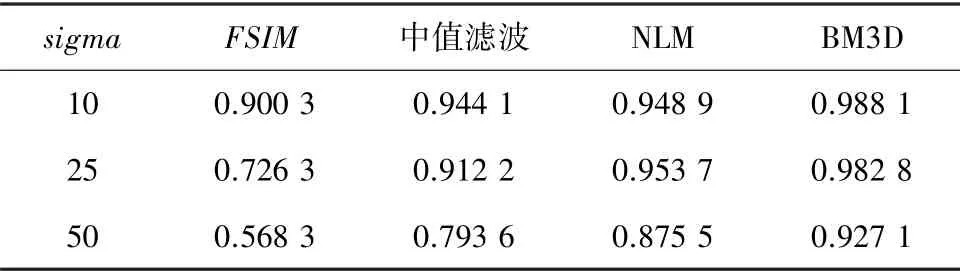
表4 不同模型对图像去噪的FSIM对比Tab.4 FSIM comparison of images denoising by different models
实验表明,BM3D针对不同大小的高斯噪声都有较好的去噪效果,满足天文图像的去噪需求。
3 结束语
将BM3D算法应用于射电天文图像去噪,相比之前的传统算法,BM3D算法有着良好的表现,在有效去除大量图像的噪声的同时,还能较为精准地恢复图像的细节特点。但其复杂度是NLM的3倍,处理图像所消耗的时间也就更长,不能做到实时处理。未来的研究需要在不降低其精准度的情况下,减少BM3D算法消耗的时间。
