基于对话框编写实现坐标方位角正算与反算的程序

李香清

(1.兰州市勘察测绘研究院，甘肃兰州 730030； 2.兰州市地理信息中心，甘肃兰州 730030)

基于对话框编写实现坐标方位角正算与反算的程序

李香清1，2∗

(1.兰州市勘察测绘研究院，甘肃兰州 730030； 2.兰州市地理信息中心，甘肃兰州 730030)

通过Visual C++6.0来设计坐标正反算的程序，基于对话框来编写，特别是在控制网平差计算中，用来坐标方位角的推算和平面坐标的正反算，在导线测量中，通过坐标的正反算来确保控制网的精度。该程序可以广泛应用于施工放样等相关工作中，并且用实际的测量工作验证了其准确性和实用性。

坐标正反算；Visual C++；坐标方位角；导线测量

1 引 言

在实际测量工作时，比如在市政工程施工测量中，经常会遇到根据已知导线控制点，利用经纬仪、钢尺测设待定点的实际问题，解决此类问题往往需要计算坐标方位角或距离，如何能够更快、更准确的利用程序实现坐标方位角的正算与反算是一个亟待研究的问题。

2 相关概念

2.1 方位角

由直线一端的基本方向起，顺时针方向至该直线的水平角度称为该直线的方位角。方位角的取值范围是0°～360°。下面介绍相关的三种方位角:

真方位角:由真北方向起算的方位角，用A表示。坐标方位角:由坐标北方向起算的方位角，用a表示。磁方位角:由磁北方向起算的方位角，用Am表示。

2.2 方位角之间的相互换算

由于三个指北的标准方向并不重合，所以一条直线的三种方位角并不相等，它们之间存在着一定的换算关系。如图1所示，一条直线的真方位角A、磁北方位角Am、坐标方位角a之间有如下的关系式，式中的δ为磁偏角，γ为子午线收敛角。

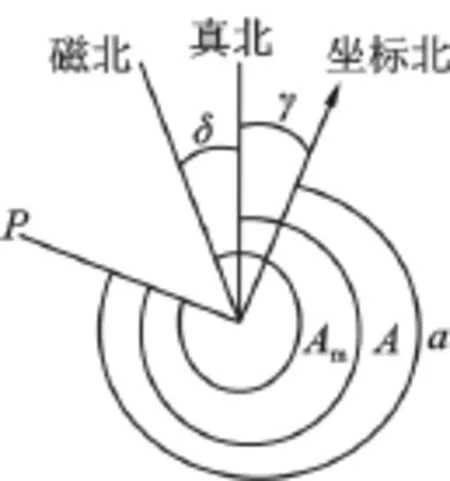
图1 三种方位角的关系

关系表达式如下:

2.3 正、反坐标方位角

一条直线的坐标方位角，由于起始点的不同而存在着两个值。如图2所示，P1、P2为直线P1P2的两端点，a12表示P1P2方向的坐标方位角，a21表示P2P1方向的坐标方位角。a12和a21互为正、反坐标方位角。若以a12为正坐标方位角，则称a21为反坐标方位角。由于在同一高斯平面直角坐标系内各点处坐标北方向均是平行的，所以一条直线的正、反坐标方位角相差180°，即a12=a21±180°。

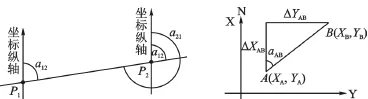
图2 正、反坐标方位角 图3 坐标正、反算示意图

3 平面直角坐标正、反算

如图3所示，设A为已知点，B为未知点，当A点坐标(XA，YA)、A点至B点的水平距离SAB和坐标方位角aAB均为已知时，则可求得B点的坐标(XB，YB)，通常称为坐标正算问题。

由图可知坐标正算的公式为:

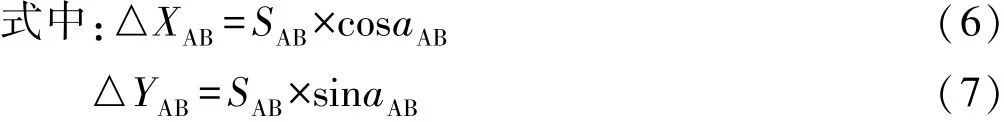
所以上面的式子可以写成:

式中的△XAB和△XAB称之为坐标增量。

同理可以得出坐标反算的公式，设A、B两已知点的坐标分别为(XA，YA)和(XB，YB)，则这条直线AB的坐标方位角aAB和水平距离SAB分别为:

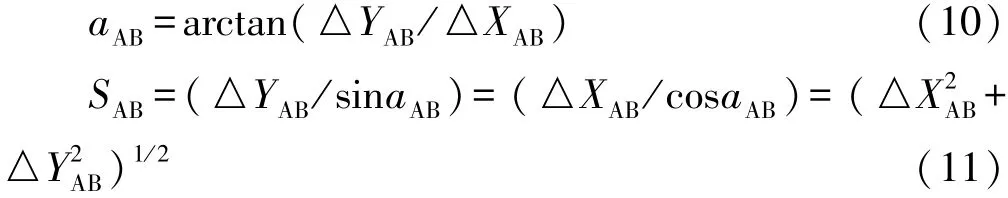
应当指出，在上面的式子中△XAB和△YAB应该取绝对值，计算得到的为象限角R，象限角取值范围为0°～90°。而测量工作中通常用坐标方位角表示直线的方向，因此，计算出象限角R后，应该将其转换为坐标方位角，其转换方法表1。

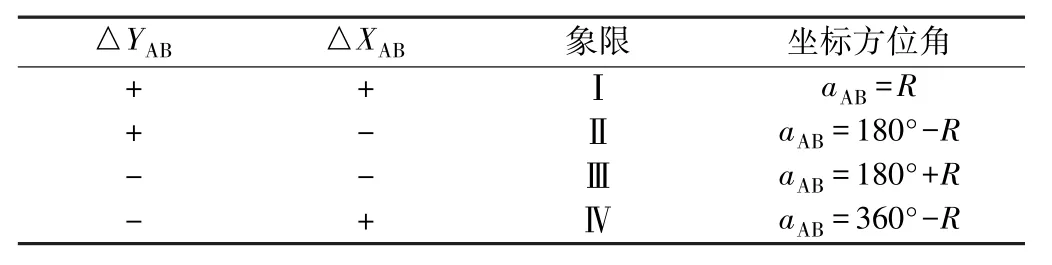
象限角转换成坐标方位角 表1

4 Visual C++6.0编程设计

4.1 对话框界面的设计

图4 对话框的界面设计

4.2 坐标正算程序的核心代码

void Czbzs::OnButtonEqual2()//响应坐标正算按钮

{

//TODO:Add your control notification handler code here

UpdateData(true)；//获得输入数据

i=m_44； //坐标方位角获取

//为减少运算，先计算几种特殊情况

if(i==0｜｜i==360)

{

m_55=m_11+m_33；

m_66=m_22；

｝

else if(i==180)

{

m_55=m_11-m_33；

m_66=m_22；

｝

else if(i==90)

{

m_55=m_11；

m_66=m_22+m_33；

｝

else if(i==270)

{

m_55=m_11；

m_66=m_22-m_33；

｝

else if(i＞0＆＆i＜90)//第一象限角

{

j=(m_44∗PI)/180；//角度转换为弧度

m_55=m_11+m_33∗cos(j)；//由表一和公式8、公式9综合

m_66=m_22+m_33∗sin(j)；

｝

else if(i＞90＆＆i＜180)//第二象限角

{

j=((m_44-90)∗PI)/180；

m_55=m_11+m_33∗(-cos(j))；

m_66=m_22+m_33∗sin(j)；

｝

else if(i＞180＆＆i＜270)//第三象限角

{

j=((m_44-180)∗PI)/180；

m_55=m_11+m_33∗(-cos(j))；

m_66=m_22+m_33∗(-sin(j))；

｝

else if(i＞270＆＆i＜360)//第四象限角

{

j=((m_44-270)∗PI)/180；

m_55=m_11+m_33∗cos(j)；

m_66=m_22+m_33∗(-sin(j))；

｝

UpdateData(false)；//更新显示

｝

4.3 坐标反算程序的核心代码

void Czbfs::OnButtonEqual()//响应坐标反算按钮

{

//TODO:Add your control notification handler code here

UpdateData(true)；//获得输入数据

dx=m_3-m_1；

dy=m_4-m_2；

az1=dxdy_az(dx，dy)；//计算坐标方位角

az=radio_to_angle(az1)；//弧度转换为角度

s=dist(dx，dy)；//计算距离

m_5=m_9；

m_6=m_10；

m_7=az1；

m_8=s；

UpdateData(false)；//更新显示

｝

double Czbfs::dxdy_az(double dx，double dy)//坐标方位角计算

{

double R，az；

R=atan(dy/dx)；//公式10

if(dx==0)//特殊情况

{

if(dy＞0)

az=PI/2；

else

az=3∗PI/2；

｝

else if(dx＞0)//由表一得出az与R关系

{

if(dy＞0)

az=R；

else

az=R+2∗PI；

｝

else

az=PI+R；

return(az)；

｝

double Czbfs::radio_to_angle(double radio)//弧度转换为角度

{

double a1，a2，angle；

int d，f，m；

a1=radio∗180/PI；

d=int(a1)；//计算度

a2=(a1-d)∗60；

f=int(a2)；//计算分

m=int((a2-f)∗60)；//计算秒angle=d+f/100.0+m/10000.0；

return(angle)；

｝

double Czbfs::dist(double dx，double dy)//计算距离

{

return(sqrt(dx∗dx+dy∗dy))；

｝

5 运行结果

将外业实测数据进行坐标方位角的推算和平面坐标的正反算，通过坐标的正反算来确保控制网的精度。在坐标反算主界面中输入起点:1点坐标(4053345.321，486456.321)，终点2点坐标(4053323.678，486123.443)，通过计算得出坐标方位角(弧度)为4.64746249773597，1点到2点的距离为333.580848270678；在坐标正算主界面中输入起点:1点坐标(4053321.476，485123.443)，距离334.756，坐标方位角(角度)213.342，通过计算得出终点坐标为(4053041.81926841，484939.449271809)。计算结果如图5所示:

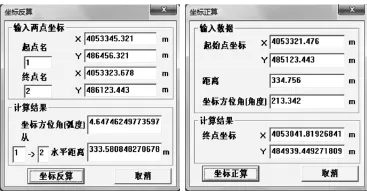
图5 坐标正反算的验证结果

6 结 论

本文通过对坐标正反算的验证得出该程序的可靠性与实用性，基于对话框编写的该程序，界面直观简洁，使计算方位角的工作变得简单易行，实现坐标方位角的正反算更加方便快捷，可以广泛应用于工程测量的施工放样及相关工作中，大幅降低了测绘工作量。

[1] 潘正风，杨正尧，程效军等.数字测图原理与方法[M].武汉大学出版社，2004.

[2] 王育坚.Visual C++面向对象编程教程[M].清华大学出版社，2007.

[3] 沈晶，刘海波，周长建.Visual C++数字图像处理典型案例详解[M].机械工业出版社，2012.

[4] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉大学出版社，2003.

[5] 陈天华.面向对象程序设计与Visual C++6.0教程题解与实验指导[M].清华大学出版社，2006.

[6] 张正禄.工程测量学[M].武汉大学出版社，2005.

Based on the Dialog Box to W rite the Program to Realize Direct and Inverse Calculation of Geodetic Coordinates and Azimuth

Li Xiangqing1，2
(1.Lanzhou Istitute of Survey and Investigation，Lanzhou 730030，China；2.Lanzhou Geographic Information Center Gansu，Lanzhou 730030，China)

Through the Visual C++6 to design the inverse coordinate calculation program，based on the dialog box to write，especially the calculation in the control network adjustment，and to calculate the coordinate azimuth angle and plane coordinates calculation，in a traverse，through coordinate and ensure the precision of the control network.This program iswidely used in construction lofting and related work and verified its accuracy and reliability by using examples.

direct and inverse calculation of coordinates；visual C++；coordinate azimuth；traverse survey

1672-8262(2013)05-137-03

P209

B

2013—06—28

李香清(1978—)，女，工程师，现从事地理信息空间数据质量检查、GIS应用研究及开发等。