基于图像分解的PCB图像去噪算法研究
2022-09-28胡涛,茅健
胡 涛,茅 健
(上海工程技术大学 机械与汽车工程学院,上海 201620)
0 引 言
印刷电路板(printed circuit board,PCB)是电子设备的重要组成部分。由于PCB板的加工工艺复杂,且板表面线路孔位密集,使得生产出的PCB板难免存在一些缺陷。自动光学检测(automatic optic inspection,AOI)设备替代传统人工目检的方式,已成为工业中应用广泛的视觉检测设备。在PCB缺陷检测环节中,由于受到现场环境、采集设备的干扰,使拍摄的图像存在一些噪音。为保证后续对图像做缺陷检测的准确度,需要先对PCB图像进行去噪处理。
在图像处理领域,传统的图像去噪算法主要有:均值滤波、中值滤波和高斯滤波等。但这些算法的去噪效果并不理想,会造成图像中细节信息的丢失。近年来,出现了一些新型的图像去噪算法,其中包括:TV算法、NLM算法、双边滤波(Bilateral Filtering,BF)算法和小波去噪算法等。这里,TV算法是一种基于各向异性的去噪算法,具有较好的去噪效果,能有效保留图像的边缘纹理等细节信息,但该算法会导致图像产生“阶梯效应”;NLM算法是根据图像块之间相似性分配权重,通过对邻域像素进行加权平均来计算中心像素点的像素值,从而达到去噪目的,但该算法计算复杂度较高,计算耗时。
基于上述研究成果,国内外专家学者对去噪算法进行了深入研究,提出了很多相应的改进方法。如:文献[10]中提出,将马氏距离作为计算图像块相似性的NLM去噪算法,在获得与原NLM算法相同的去噪效果下,一定程度上缩短了图像去噪耗时。文献[11]对NLM算法相似性度量的方法进行改进,提出同时考虑图像像素的空域信息、像素相似性和像素差均值,来计算新的权重,改进后的算法对多种噪音均有较好地去除效果。文献[12]提出先对图像采用NLM算法进行滤波,提取去噪后图像先验信息,根据先验信息设计自适应的全变分去噪模型,去噪效果相较于原有去噪算法有所提升。文献[13]提出首先采用分数阶全变分模型获得精确的残差图像,根据残差图像的方差,区分出图像的纹理和平坦区域,选用不同的保真项参数进行图像去噪,较好地保持了图像的边缘和细节信息。文献[14]提出一种混合去噪模型,通过值确定最优加权参数,分配维纳滤波模型和改进全变差模型的权重,实现对图像的去噪,有效保护了图像的边缘细节信息。
综合上述图像去噪算法的优缺点,本文提出了一种基于图像分解的PCB去噪算法。该算法对全变分(Total Variation,TV)算法进行改进,设计了一种基于范数的正则项去噪模型;将改进的TV算法和非局部均值(Non Local Mean,NLM)算法相结合,对图像去噪开展研究,使图像的边缘信息和“阶梯效应”得到很好的处理。
1 基于图像分解的PCB图像去噪算法
本文PCB去噪算法主要包括PCB图像分解、纹理部分去噪和结构与纹理部分融合三部分。通过分析传统TV算法在处理图像时会产生“阶梯效应”现象,设计了一个基于范数的正则项去噪模型对PCB图像进行分解,得到结构和纹理两个部分。其中,结构部分包含图像中较大尺度的对象,纹理部分包含图像的噪音和细小尺度的细节信息。使用NLM算法来去除纹理部分中的噪音。最后,将结构部分和纹理部分融合,得到最终的PCB去噪图像。
1.1 基于改进TV的图像分解
通过使用图像去噪算法来对图像进行分解是目前常用的方法。Rudin等人提出了一个经典的TV去噪算法,将含噪音的图像分为无噪声图像和噪音两部分组成,即。则TV去噪模型为:
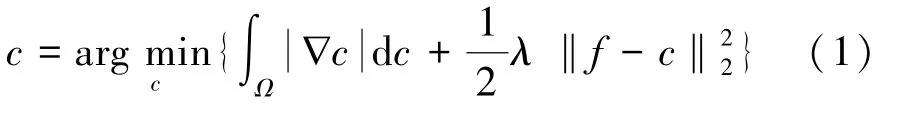

由于直接对该去噪模型求解较为困难,通常将其转化为Euler-Lagrange方程进行求解,其结果如下:
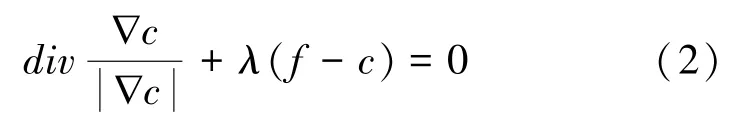
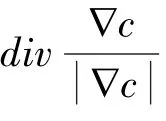
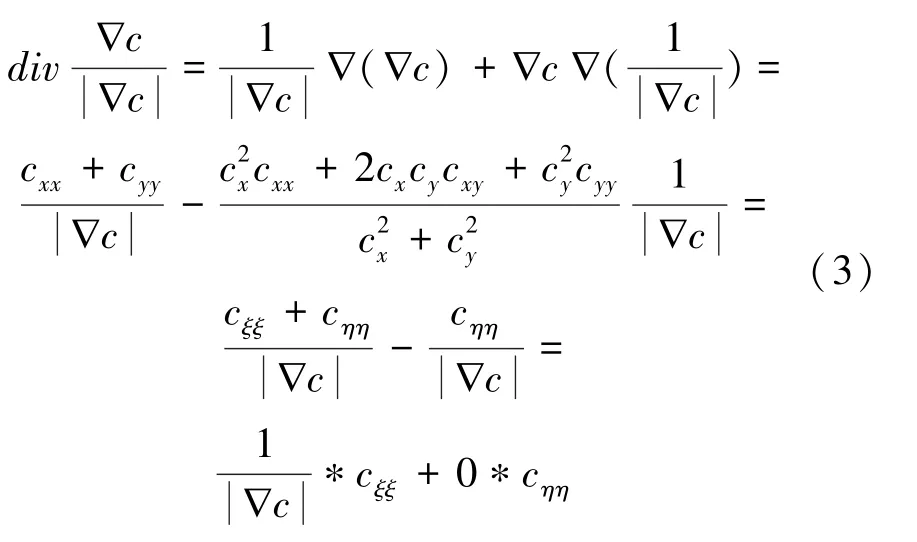
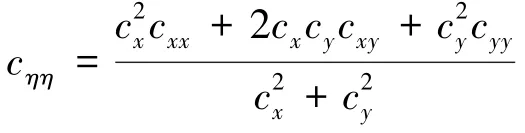
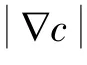
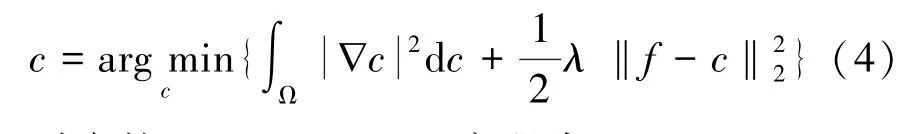
对应的Euler-Lagrange方程为:
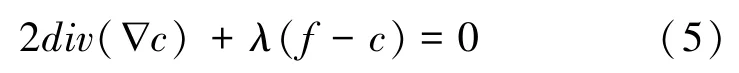
对(∇)进行分解得:
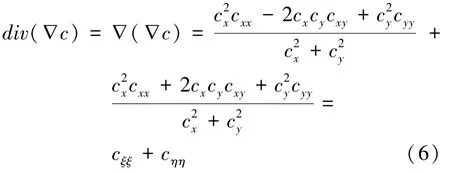
从式(6)中可以看出,c和c的系数均为1,说明改进的TV算法是属于各向同性扩散模型。各向同性扩散模型可以有效避免阶梯效应,但在去噪的同时,会导致图像边缘的模糊化。
由于传统迭代方法速度较慢,本文使用Split Bregman迭代框架对提出的去噪模型进行求解,可以显著降低计算的复杂度。由此对式(5)进行转换得:
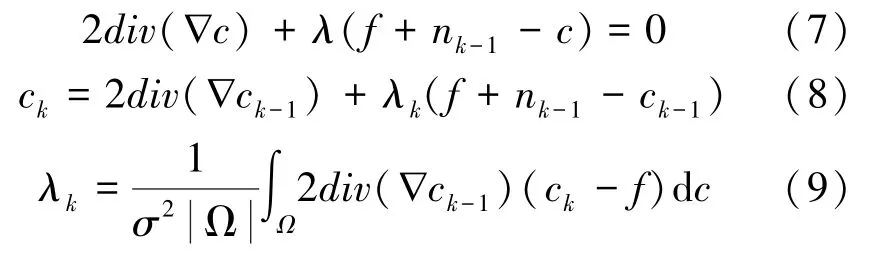
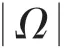
通过采用改进的TV去噪算法对PCB图像进行分解,其结果如图1所示。

图1 PCB图像分解过程Fig.1 PCB images decomposition process
1.2 NLM去噪算法
NLM算法的核心思想是:图像内像素点都由其邻域内的像素块来描述,通过计算各个像素块之间的相关度来分配权重,对邻域内的像素点进行加权求和,得到新的像素值,从而实现去噪目的。
算法流程如下:给定一幅带噪音的图像{(,)(,)∈},通过NLM算法得到滤波后的图像,该图像是由其邻域内像素点的加权平均得到。公式为:
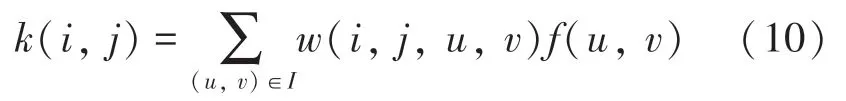
其中,(,,,)表示像素点(,)在其窗口邻域{(,)∈}内其它像素点对(,)相似度的权重,该权重需满足以下条件:
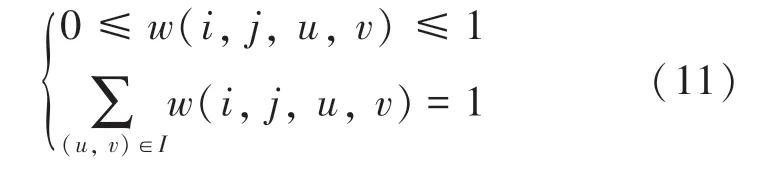
权重(,,,)的计算公式为:
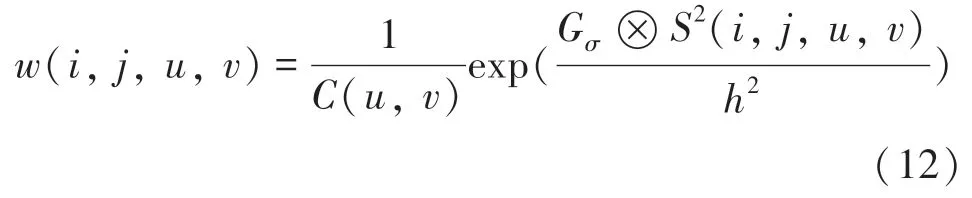
这里,(,)可由下式计算求得:
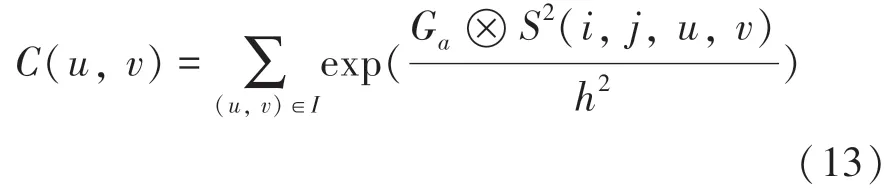
其中,G是标准差为的高斯核;(,,,)表示搜索窗口内像素块之间的欧式距离;为图像的平滑系数;(,)是权值的归一化系数。
1.3 去噪图像质量评价
为了验证本文算法对PCB图像去噪效果的好坏,采用主观视觉评价和客观评价相结合的评价方法。客观评价采用峰值信噪比(Peak Signal to Noise Ratio,)和结构相似度(Structural Similarity Index Measurement,)两种图像质量评价指标。
方法是目前普遍使用的一种图像客观评价指标。取值为正数,值越高,图像质量越好。对此定义可表示为:
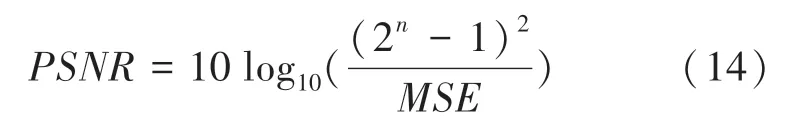
其中,表示图像和的均方误差。具体定义式可写为:
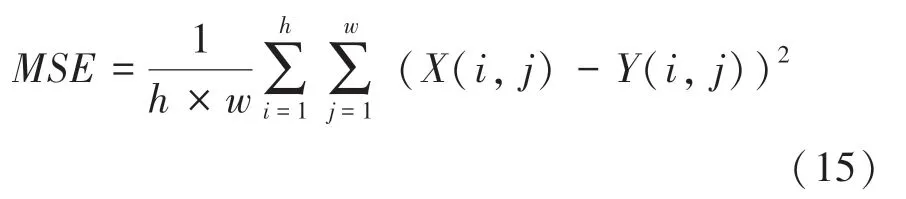
评价法是一种衡量2幅图像相似度的指标,由亮度相似性评价、对比度相似度评价、结构相似度评价三部分组成。其取值范围为0~1,值越大、则图像质量越好,反之质量越差。推导得到的数学定义式见如下:
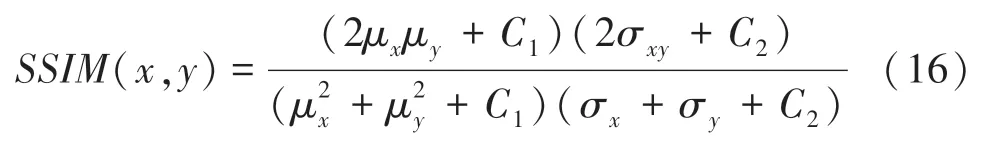
其中,μ、μ为2张图像的平均强度;σ、σ为两图像的标准差;σ为两图像之间的互相关系数。
2 实验结果与分析
本文实验平台为Windows10操作系统,CPU2.4 GHz,内存16 GB;编程环境为Matlab 2019a。选取5组图像,其中包含4组PCB图像,像素大小为600 pixel×600 pixel,以及1张人物图像,像素大小为512 pixel×512 pixel。并为这5组图像添加标准差为10的高斯白噪音。为了验证本文提出的基于图像分解的PCB去噪模型的有效性和可行性,将本文提出的去噪算法与改进TV算法、传统TV算法和NLM算法,分别对实验图像进行去噪处理,并对实验结果进行对比分析。
图2是4种去噪算法对含噪音的PCB图像处理的结果。从主观视觉来看,改进TV算法和传统TV算法去噪的效果较差,虽然都有效去除了高斯噪音,但同时也导致图像很多细节信息的丢失,图像中大部分的小孔被模糊,图像整体效果不太清晰。NLM算法和本文算法去噪效果比较显著,均过滤掉图像的噪音,图像的细节信息保护得很好,原图中排列的很多细微的小孔都得到了保留。

图2 PCB图像去噪结果比较Fig.2 Comparison of PCB images denoising results
考虑到基于主观视觉评价对去噪结果的细微差异无法进行很好的辨别,所以结合客观评价的方法是很有必要的。表1和表2统计了5组图像在4种去噪算法处理后,采用和评价指标对去噪效果进行评价的结果。从表1、表2中可以看出,实验的5组图像中,本文算法的和值均最高。通过计算5组图像和的平均值得出,本文算法的相较于TV算法、改进TV算法和NLM算法分别提高了9.0%、10.8%和1.4%;本文算法的相较于TV算法、改进TV算法和NLM算法分别提高了7.0%、8.6%和1.1%。
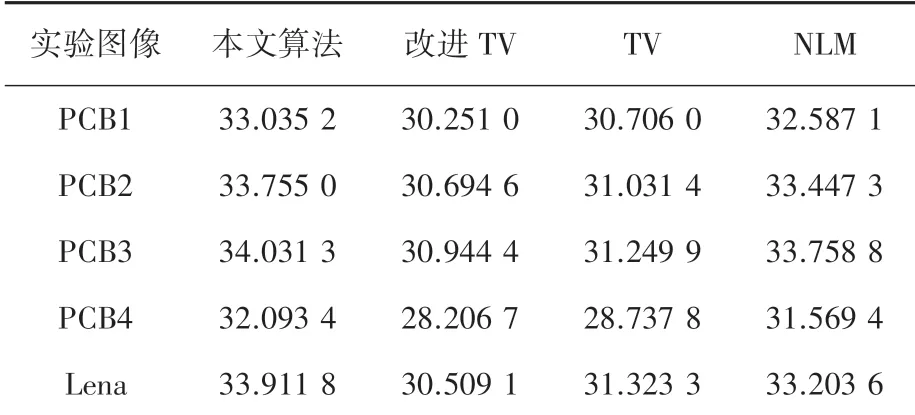
表1 图像去噪后的PSNRTab.1 PSNR after images denoising

表2 图像去噪后的SSIMTab.2 SSIM after images denoising
综合上述主观视觉评价和客观评价的结果,充分验证了本文所提算法的有效性。
3 结束语
为了更好地消除PCB图像中的噪音,本文提出了一种基于图像分解的PCB去噪算法。通过实验证明了本文所提算法的有效性。此外,相较于传统的图像去噪算法,本文算法的去噪效果和对图像细节保护能力更佳。
