G-纯正合复形的相关刻画

魏宝军, 于春艳, 杨晓燕

(重庆对外经贸学院 数学与计算机学院, 重庆 合川 401520)

纯这一概念在代数和模理论研究中扮演着重要的角色.纯性是阿贝尔群理论中的一个重要概念,其中有足够纯内射群和足够纯投射群,这使得可以利用同调方法对纯进行更深层次的探究.然而复形范畴是一个有足够多投射对象和足够多内射对象的Abel 范畴,因此Gorenstein同调理论在复形范畴中可以形成一种新的理论体系.1998 年,Enochs等[1]引入了Gorenstein投射复形的概念,证明了在Gorenstein环上的这些复形就是Gorenstein投射模的复形.2011年,Yang等[2]证明了在任意环上复形P是Gorenstein投射(内射)的当且仅当P的每一层次上的模是Gorenstein投射(内射)模,并给出了一系列相关的等价刻画.

2017年,Yu等[3]在定义了相对于Gorenstein投射模范畴中的纯正合列,即G-纯正合列,并得到了相关的一系列性质和应用.随着纯领域的深入研究,本文通过前面对Gorenstein投射复形范畴中的纯正合列,即定义了G-纯正合复形的研究,主要对G-纯正合复形相关的等价刻画作了进一步研究.

1 预备知识

除非特别声明,环R是具有单位元的结合环,所有涉及的模均是酉模,ModR表示左R-模范畴.对未作解释的标记,事实和概念,请参见文献[4].

定义 1[5]如果正合复形F:…→Fn+1→Fn→Fn-1→…是G-纯正合的,则满足以下两条:

1) 对任意的n∈Z,Fn是Gorenstein投射的;

2) 对任意的n∈Z,模的短正合列0→ZnF→Fn→Zn-1F→0是G-纯正合的.

性质 1[5]1)H如果为GProjC(R)中的纯投射复形,则对复形的任意G-纯正合列0→F1→F2→F3→0,序列

0→HomC(R)(H,F1)→HomC(R)(H,F2)→
HomC(R)(H,F3)→0

是正合的.

2)E如果为GProjC(R)中的纯内射复形,则对复形的任意G-纯正合列0→F1→F2→F3→0,序列

0→HomC(R)(F3,E)→HomC(R)(F2,E)→
HomC(R)(F1,E)→0

是正合的.

3)A如果为GProjC(R)中的绝对纯复形,则GProjC(R)中任意的正合列0→A→F2→F3→0是G-纯正合的.

将GProjC(R)中的纯投射、纯内射和绝对纯复形构成的GProjC(R)的全子范畴分别记为PP-GProjC(R),PI-GProjC(R)和Abs-GProjC(R).

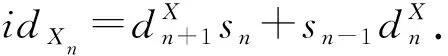
定义 3[4]称R-模的序列

定义 4[6]称小范畴I是filtered,如果满足以下两个条件：

1) 对I的任意两个对象i、j,存在对象k,使得HomI(i,j)和HomI(j,k)是非空的.

2) 对I的任意两个对象i、j和两个平行同态f,g∈HomI(i,j),存在对象k和同态h∈HomI(j,k),使得hf=hg∈HomI(i,k).

引理 2[6]设X、Y是链复形.若满足：

1) 对任意的整数n,HomR(Xn,Y)是正合的;

2) 对任意的整数n≪0,HomR(Xn,Yn)是平凡群.

则链映射f:X→Y是零伦的.

定义 5如果任意Gorenstein投射R-模可写成有限表示Gorenstein投射模的正向极限,称环R满足(*)条件.

例子 11) Artian代数是满足(*)条件的[3].

2)n-完全的Ding-Chen环是满足(*)条件的[7].

2 Gorenstein投射复形范畴中的纯正合列

000↓↓↓0→N'→N→N″→0↓↓↓0→P'→P'P″ →P″→0π'↓π↓π″↓0→M'π→Mp→M″→0↓↓↓000

证明因为p*:HomR(P″,M)→HomR(P″,M″)是满的,所以存在映射f:P″→M,使得pf=π″.因此由线性映射π=[τπ′,f]:P′⊕P″→M可得到如下行正合的交换图.

0→P'→P'P″ →P″→0π'↓π↓π″↓0→M'τ→MP→M″→0

取N=Kerπ,由蛇引理得到上述行列正合的交换图.又因为左右两列的短正合列是G-纯正合的,所以中间一列的短正合列也是G-纯正合的.

引理 4设R满足(*)条件,C是有限表示Gorenstein投射模构成的复形,P是一个可缩复形且P的每一个合冲模是有限表示Gorenstein投射模的直和.考虑链映射g:C→P,则存在一个可缩复形P′⊆P,其中P′是每个层次由有限表示Gorenstein投射模构成的,使得Img⊆P′.如果复形C是左有界(右有界,有界),那么子复形P′也是左有界(右有界,有界).

证明假设对任意的正整数n,存在有限表示Gorenstein投射模{Qn}n∈Z,使得Pn=Qn⊕Qn-1,其微分dp:Pn→Pn-1是映射

Qn⊕Qn-1→Qn-1⊕Qn-2,

(xn,xn-1)(xn-1,0),

g(Cn)⊆Q‴n⊕Q‴n-1.

因此P的可缩复形可以通过g合成,对于所有的n,其中P的n-层次上的模是有限表示Gorenstein投射子模且

Q‴n⊕Q‴n-1⊆Qn⊕Qn-1=Pn.

定理 1设R满足(*)条件.则对任意的Gorenstein投射复形F,以下条件等价:

1)F是G-纯正合的;

2) 对任意的有限表示Gorenstein投射模C,有HomR(C,F)是正合的;

3) 任意从有限表示Gorenstein投射模的右有界复形到F的链映射是零伦的;

4)F是正合的且对每个层次都是G-纯满的任意链映射f:Y→F,对任意的有限表示Gorenstein投射模的右有界复形C,链映射C→F可通过f分解;

5) 任意从有限表示Gorenstein投射模的右有界复形到F的链映射能通过有限表示Gorenstein投射模的右有界可缩复形分解;

6) 任意从有限表示Gorenstein投射模的有界复形到F的链映射能通过有限表示Gorenstein投射模的有界可缩复形分解;

7)F是有限表示Gorenstein投射模的有界可缩复形的一个filtered上极限.

证明1)⟹2) 设C是有限表示Gorenstein投射模.因为F是G-纯正合的,所以对任意的n∈Z,存在GProjR模中的短正合列0→ZnF→Fn→Zn-1F→0,则

0→HomR(C,ZnF)→HomR(C,Fn)→
HomR(C,Zn-1F)→0

2)⟹3) 由引理6可得.

3)⟹4) 因为任意的从有限表示Gorenstein投射模的右有界复形到F的链映射是零伦的,所以对任意的R[n]也成立.故F是正合的.

设C是有限表示Gorenstein投射模的右有界复形.考虑链映射g:C→F.假设存在g与零映射之间的同伦Σ,使得g=dFΣ+ΣdC.因为f:Y→F是每个层次由G-纯满同态构成的链映射,所以在每个层次存在映射S:C→Y,使得Σ=fS.因此

h=dYS+SdC:C→Y

是一个链映射.又因为dYh=dYSdC=hdC,所以

fh=f(dYS+SdC)=fdYS+fSdC=
dFfS+fSdC=dFΣ+ΣdC=g.

4)⟹5) 设F是正合复形.构造一个对子(P,π),若对任意的n,Qn是有限表示Gorenstein投射模的直和且Qn→ZnF是G-纯满态射,则由引理4可得到如下交换图.

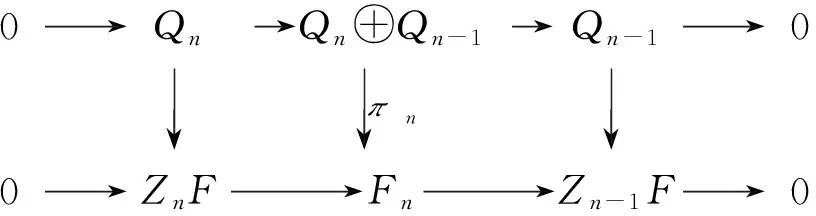
0→Qn→QnQn-1 →Qn-1→0↓πn↓↓0→ZnF →Fn→ Zn-1F→0

5)⟹6) 设C→F是链映射,其中C是有限表示Gorenstein投射模构成的有界复形.由5)可知,链映射C→F可以通过有限表示Gorenstein投射的有界可缩复形P分解为C→P→F的合成.因为C是有界复形,所以由引理4知,Img⊆P′,其中P′是有限表示Gorenstein投射模的有界可缩复形.

ζ=ζ

是链映射,使得f是合成

其中(P,f)是中的任意对象,η(P,f)是Γ(P,f)到的自然映射.

则对子(P⊕P′,[f,f′])是中的对象且自然映射τ:P→P⊕P′和τ′:P′→P⊕P′是中的态射.因此有如下交换图.

Pτ→ PP'τ'←P'f↓[f,f']↓ f'↓FFF

下证ζ每一个层次是满的.

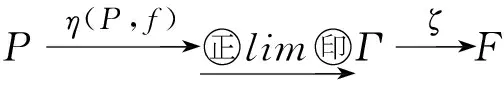
再证ζ每一个层次是单的.

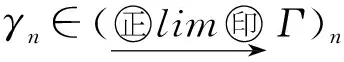
γn=η(Q,g)(tn).

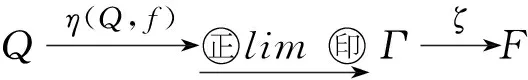
gn(tn)=0∈Fn.

考虑可缩链复形P,其中P的第n和n-1层次为R，其他层次为0.则存在唯一的链映射h:P→Q,其中h(1)=tn.则有范畴中的如下交换图.

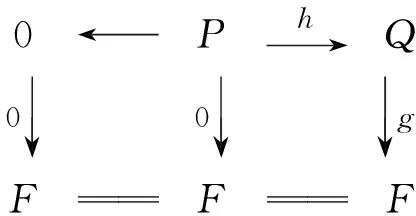
0←Ph→Q0↓0↓g↓FFF

因此可以诱导出链复形的交换图.

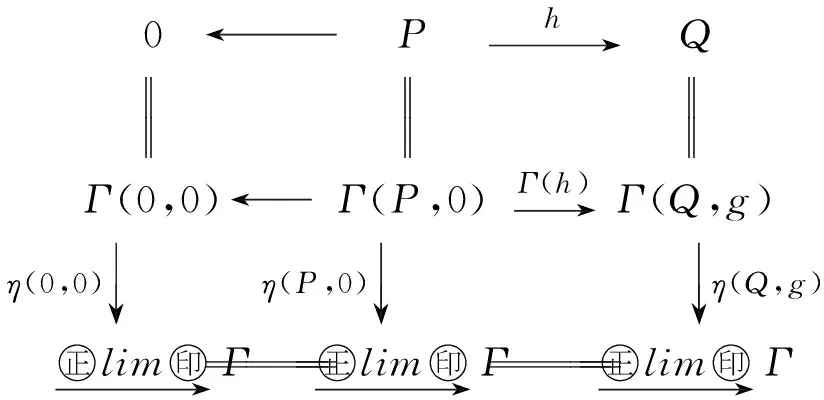
0←Ph→QΓ(0,0)←Γ(P,0)Γ(h)→Γ(Q,g)η(0,0)↓ η(P,0)↓ η(Q,g)↓㊣lim㊞→ Γ㊣lim㊞→ Γ㊣lim㊞→ Γ

于是易得tn∈Kerη(Q,g).故

γn=η(Q,g)(tn)=0.

设(P,f)和(P′,f′)是中的两个对象,a,b:(P,f)→(P′,f′)是两个平行态射.则a,b:P→P′是两个链映射,使得f′a=f=f′b.因为f′(b-a)=0,所以f′可通过C=Coker(b-a)分解为其中p是商映射.因为C是有限表示Gorenstein投射模的有界复形,所以存在有限表示Gorenstein投射模的有界可缩复形P″,使得分解为

于是有下面交换图.

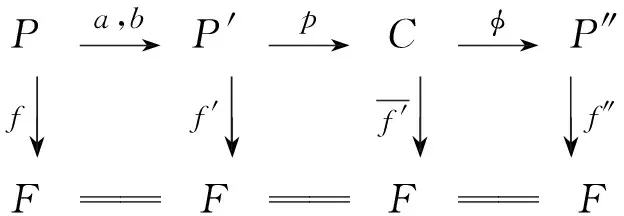
Pa,b→P'p→Cϕ→P″f↓f'↓f'↓f″↓FFFF

故对子(P″,f″)也是的一个对象,链映射c=φp是ζ中从(P′,f′)到(P″,f″)的态射.因为

c(b-a)=φp(b-a)=φ0=0,

所以cb=ca.

7)⟹1) 设F是有限表示Gorenstein投射有界可缩复形{Pi}i∈I的filtered上极限.因为Pi是正合的且filtered上极限是正合函子,所以复形F也是正合的.因此对任意的整数n,GProjR中的短正合列0→ZnF→Fn→Zn-1F→0是可裂短正合列0→ZnPi→Pni→Zn-1Pi→0的filtered上极限.故由引理1易知,对任意的整数n,GProjR中的短正合列0→ZnF→Fn→Zn-1F→0是G-纯正合的.

致谢重庆师范大学涉外商贸学院校级项目(GG2020010)对本文给予了资助,谨致谢意.