Fuzzy系统的函数逼近功能及误差估计
2022-09-27李洪兴
李洪兴
(1. 北京师范大学珠海校区 应用数学学院, 广东 珠海 519085;2. 大连理工大学 控制科学与工程学院, 辽宁 大连 116024)
1 预备知识
熟知,Fuzzy集合是由L.A.Zadeh于1965年首次提出的,随后,基于Fuzzy集所形成的Fuzzy推理以及使用Fuzzy推理所构造的Fuzzy系统的研究工作逐渐展开,Fuzzy系统的应用范围逐渐扩展.其中,Fuzzy系统的函数逼近功能是一个十分有意义的研究方向.从数学的观点看,一个Fuzzy系统实际上是从输入论域到输出论域的一个映射; 特别,当输入论域和输出论域都是实空间时,该Fuzzy系统就是一个实函数,它当然可以近似逼近某个实函数.文献[1]已经显示了Fuzzy系统函数逼近的雏形,文献[2]证明了Fuzzy系统的插值机理,而文献[3]揭示了Fuzzy系统的概率论意义.本文将从Fuzzy系统的具体构造出发讨论Fuzzy系统的函数逼近功能,同时还要研究这种函数逼近的误差估计.
值得指出的是,许多文献也在讨论Fuzzy系统的泛逼近性,但是它们都是基于所谓简略推理法得到的非含参积分形式的推理结果,这样的推理结果是不合理的,也是不准确的.而本文的推理结构是源于条件数学期望得到的推理结果,是一种最小二乘最优的推理结果.
2 Fuzzy系统的结构
首先,考虑单输入单输出的开环静态系统,即SISO,如图1所示.

图1 SISO静态开环系统
s:X→Y,
xy≜s(x),
(1)
对于一个不确定性系统,常常可以通过实验或检测得到一组输入输出数据,记为
IOD≜{(xi,yi)∈X×Y|i=0,1,…,n},
成为该系统的基础数据集.根据IOD可以得到一个离散的映射
s1:X0→Y0,
xis1(xi)=yi,
i=0,1,…,n,
这里
X0={x0,x1,…,xn},Y0={y0,y1,…,yn}.
s:X→Y,
xy=s(x).
x
(2)
‖s‖≜‖s‖∞≜max{|s(x)||x∈X}.
a=x0 c=yk0≤yk1≤…≤ykn=d, σ:{0,1,…,n}→{0,1,…,n}, iσ(i)=ki, (3) 或者记为 如果没有如此的置换,如下的输出数据集 Y0={yi|i=0,1,…,n}, 一般不满足如下的全序关系 c=y1 Bi∈F(Y),i=0,1,…,n 时是必不可少的条件. A≜{Ai|i=0,1,…,n}. 类似地,采用输出数据集Y0也好获取另一组Fuzzy集 B≜{Bki|i=0,1,…,n}. kσ-1(i)=i, 从而Bi=Bkσ-1(i),这样一来,便得到 B={Bi|i=0,1,…,n}. IfxisAithenyisBi,i=0,1,…,n, (4) 这里Ai和Bi分别是定义在X和Y上的Fuzzy集,即 Ai∈F(X),Bi∈F(Y), i=0,1,…,n. Ri∈F(X×Y), ∀(x,y)∈X×Y, μRi(x,y)≜θ(μA(x),μB(y)), 这里 θ:[0,1]×[0,1]→[0,1] ∧:[0,1]×[0,1]→[0,1], (a,b)∧(a,b)=a∧b. ·:[0,1]×[0,1]→[0,1], (a,b)·(a,b)=a·b. Fuzzy推理规则组(4)被视为如下的一个映射 s*:A→B, Ais*(Ai)≜Bi, i=0,1,…,n. ∀(x,y)=X×Y, μ s**:F(X)→F(Y), AB=s**(A)≜A·R, μ 接下来,为了获得如下的函数 x s**:F(X)→F(Y), s1:X→F(Y), xs1(x)≜s**({x}), (5) ∀(x,y)∈X×Y, μs1(x)(y)=μs**({x})(y)= μ (6) B(ξ=x)≜s1(x), ∀(x,y)∈X×Y, μB(ξ=x)(y)=μs1(x)(y)= (7) y=(y(ξ))ξ=x=y(x), 文献[3]已经证明了常用的清晰化方法,即重心法是合理的,并且是在最小二乘意义下是最优的方法.现在假定 使用重心法便有需要的这个点的表达式 y=(y(ξ))ξ=x= (8) 这意味着已经得到 x (9) 然后,把(7)式带入到(9)式中,便有 (10) 注 2.1注意到∀(x,y)∈X×Y,有 μB(ξ=x)(y)=μR(x,y), (11) IOD={(xi,yi)∈X×Y|i=0,1,…,n}, Δyki=yki+1-yki,i=0,1,…,n-1, Δy 由于 Δyi=Δykσ-1(i), (12) 这里已置 μ i=0,1,…,n. (13) μ i,j∈{0,1,…,n}. 构造如下的函数 f (14) 显然 f 特别地,当Δyi=h(i=0,1,…,n),即 Y0={yi|i=0,1,…,n} 是等距分割的数据集时,其中通用的间隔h>0,并且不难验证满足条件 那么有 μ i=0,1,…,n. (15) 进一步,(12)和(14)式可以简化为 (16) f FIOD≜ {(Ai,Bi)∈F(X)×F(Y)|i=0,1,…,n}, 如果它满足条件 μAi(x)∈C(X),μBi(y)∈C(Y), i=0,1,…,n, ∃i∈{0,1,…,n-1},μAi(x)+μAi+1(x)=1; ∃j∈{0,1,…,n-1},μBj(x)+μBj+1(x)=1. Ai(x Bi(y 注 2.2不难验证,当FIOD具有二相性时,前面得到的结论仍然有效. 回过头来,再考察数据集 IOD={(xi,yi)∈X×Y|i=0,1,…,n}. 引入记号 Δxi≜xi+1-xi,i=0,1,…,n-1, 显然 反之不然,即 yi=s(xi), FIOD= {(Ai,Bi)∈F(X)×F(Y)|i=0,1,…,n}. (17) 这里假定满足条件 yi=s(xi), (18) 引理 3.1设f(x,y)是X×Y上的一个二元连续函数,其中 X=[a,b],Y=[c,d], 对于下面的含参积分 c=y0 只要 (19) 证明倘若不然,那么∀ε>0,取 δk=1/k,k=1,2,…, c=y(k)0 同时存在 ξ(k)i∈[y(k)i,y(k)i+1],i=0,1,…,n-1, 尽管 λ 但是 |I(xi|≥ε. x 因为 δ 所以必有 0<ε≤ 这显然是个矛盾,故引理为真. 引理 3.2设f(x,y)∈C(X×Y),这里 X=[a,b],Y=[c,d]. 如果∀x∈X,I(x)>0,则∃δ>0,使得关于Y的任何一个分割 c=y0 以及任意选取的ξi∈[yi,yi+1],如下的I(x)的Riemann和式一定满足下面的蕴涵式 (20) 证明首先,不难理解下式 I(x)≥I(x0) 为真.今取 ε=I(x0), c=y0 以及任意选取的ξi∈[yi,yi+1],如下的I(x)的Riemann和式必满足结果:只要 I(x0)-ε=0. 因此引理的结论为真. 再从引理 3.1和引理3.2,可以获得如下的引理3.3. 引理 3.3设f(x,y)、g(x,y)是两个定义在论域X×Y上的连续函数,这里 X=[a,b],Y=[c,d], c=y0 如果 (21) 证明根据引理3.2,下面的表达式对于较大的n∈N+是有意义的: 根据极限运算规则,即商的极限等于极限的商,再利用引理3.1,便知引理3.3正确. 定理 3.1关于数据集IOD,假定如下的Fuzzy数据集满足二相性 FIOD= {(Ai,Bi)∈F(X)×F(Y)|i=0,1,…,n}. 这里满足条件 证明对于任意给定的s∈C[a,b],假定数据集IOD满足插值条件:∀i∈{0,1,…,n}, yi=s(xi). n>N1⟹‖f ‖s-fn‖ fn(x)=μ 由二相性可知 μ 因此得到 |s(x)-fn(x)|= 由此便有 |s(x)-fn(x)|≤ 即 ‖s-f 取 N=max{N1,N2}∈N+, 定理 4.1在定理3.1的条件下,对于任意的函数s∈C2[a,b],假定满足条件:∀i∈{0,1,…,n-1}, μAi,μAi+1∈C2[xi,xi+1]. yi=s(xi), 则必有下面的结论: rn(x)=s(x)-fn(x)= (22) 其中 x∈[xi,xi+1],ξi∈(xi,xi+1), i=0,1,…,n-1, 2s′(ξ s(ξ qi(x)=μAi(x)Δyi+μAi+1(x)Δyi+1. ‖rn‖∞=‖s(x)-fn(x)‖ (23) 其中 Δ Ci≜min{qi(x)|x∈[xi,xi+1]}, M M M L1i≜max L2i≜max 证明1)∀x∈[a,b],当 x=xi,i=0,1,…,n, 结论显然为真;故只考虑 x≠xi,i=0,1,…,n x∈(xi,xi+1), f μ (24) 其中 pi(x)≜μAi(x)s(xi)Δyi+ μAi+1(x)s(xi+1)Δyi+1, (25) qi(x)≜μAi(x)Δyi+μAi+1(x)Δyi+1. (26) f qi(x)>0. 接下来考虑逼近余项的表达式 rn(x)=s(x)-f 将它改写为 rn(x)qi(x)=s(x)qi(x)-fn(x)qi(x)= s(x)qi(x)-pi(x), (27) 根据插值条件可知 rn(xj)=0,j=i,i+1, 或者写为 s(xj)qi(xj)-pi(xj)=0, j=i,i+1. rn(x)qi(x)=k(x)(x-xi)(x-xi+1), (28) 进而写为 rn(x)qi(x)=k(x)(x-xi)(x-xi+1)= s(x)qi(x)-pi(x), 事实上,设x是个固定点,构造一个辅助函数 φi(t)=s(t)qi(t)-pi(t)- k(x)(t-xi)(t-xi+1), (29) φi(xj)=0,j=i,i+1, xi 为了方便起见,引入符号: φi(t)=φi1(t)-φi2(t)-φi3(t), φi1(t)≜s(t)qi(t), φi2(t)≜pi(t), φi3(t)≜k(x)(t-xi)(t-xi+1). 于是便有: rn(x)=s(x)-f i=0,1,…,n-1. |(x-xi)(x-xi+1)|≤ Ci=min{qi(x)|x∈[xi,xi+1]}. 最后,根据余项表达式便有如下的不等式 r Δyi=s′(ξi)Δxi, 即 Δyi⟺c·Δxi, ‖rn‖ 推论 4.1在定理4.1中,如果诸Fuzzy集Ai(i=0,1,…,n)具有三角波形隶属函数,则: 1) fn(x)关于s(x)逼近的余项表达式呈现为 rn(x)=s(x)-fn(x)= i=0,1,…,n-1, (30) qi(x)=Ai(x)Δyi+Ai+1(x)Δyi+1, (ξi(x)-x 2) fn(x)关于s(x)逼近的误差估计表达式呈现为 ‖rn‖ (31) 证明首先,容易了解一个事实:∀i∈{0,1,…,n-1}, 又有 r 最后可得 M 定理 5.1在定理3.1的条件下,任取连续函数s∈C[a,b],记 μBi(y),μBi+1(y)∈C1[yi,yi+1], yi=s(xi), 则有 (32) 其中 证明对于任意选取x∈X=[a,b],有下面的表达式 |f 接下来,分别考虑下面两个表达式的估计: μAks(x)+μAkt(x)=1, ∀i∉{s,t},μAki(x)≡0. 由此便有 (μAkt(x)·μBkt(y)))dy- μAks(x)yksΔyks-μAkt(x)yktΔykt|. 图2 s=t,0 Bks(y)≜μBks(y). 图3 s=t,s=0 Bk0(y)≜μBk0(y). 图4 s=t,s=n Bkn(y)≜μBkn(y). 类似地有 图5 0 因为所有的Bki都是Fuzzy数,所以在 μAks(x)μBks(y),μAkt(x)μBkt(y) ηs-1∈(yks-1,y 使得 图6 0=s μAks(x)yksΔyks-μAkt(x)yktΔykt|≤ 图7 0 μAks(x)yksΔyks-μAkt(x)yktΔykt|≤ 图8 |s-t|>1,0 图9 |s-t|>1,0=s 图10 |s-t|>1,0 μAks(x)yksΔyks-μAkt(x)yktΔykt|≤ μAks(x)yksΔyks-μAkt(x)yktΔykt|≤ 综合上述的3种情形,有 μAks(x)+μAkt(x)=1. 于是有 μAks(x)Δyks-μAkt(x)Δykt|. 综合上述3种情形,有 最后,根据1)和2)的结果,有 于是便有 这就完成了定理的证明. 推论 5.1在定理5.1中,当所有的Bi具有三角波形式的隶属函数式,则(32)式中的Γ转化为 (33) 这里 根据定理4.1和定理5.1,可以得出下面的结论. 定理 5.2在定理4.1和定理5.1的结论中,如果记则有 ‖s-fn‖∞+‖f∞= ‖rn‖ (34) 考虑函数 s(x)=sinx∈C[-3,3], 不难知道 ‖s′‖∞=‖s″‖∞=1. λ=Δx 再取 μ i=0,1,…,n, 图11 和fn(x)逼近s(x) 图12 和fn(x)逼近s(x) 可以看出:当n=6(即使用了7条推理规则),逼近的精度较低,但是曲线的光滑性不差;当n=30(即使用了31条推理规则),逼近的精度较高并且光滑性也较好.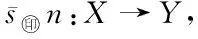

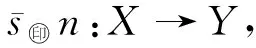

3 Fuzzy系统的函数逼近性质
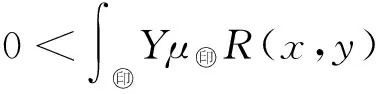









|s(x)-(μ
|s(x)(μ
(μ
μ
μ
|s(x)-s(xi)|+|s(x)-s(xi+1)|≤4 误差分析与余项估计
5 Fuzzy系统和fn(x)之间的误差估计
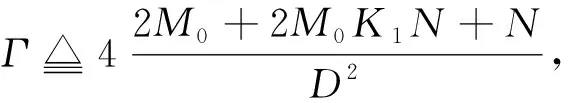

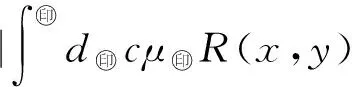








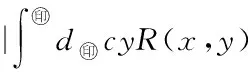


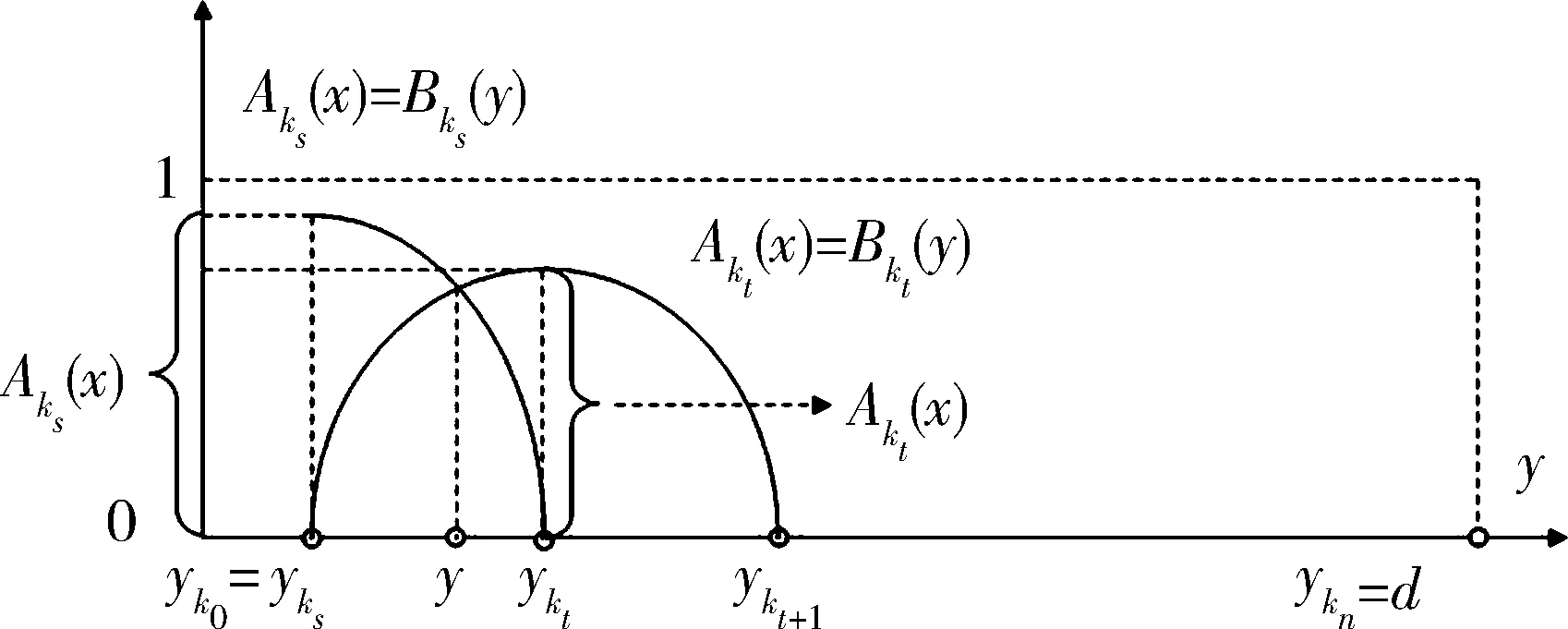



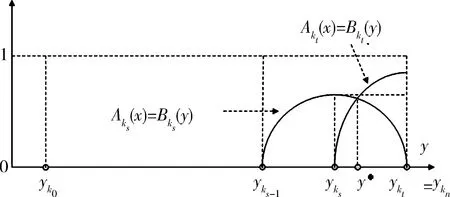

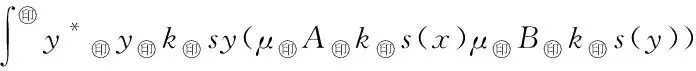





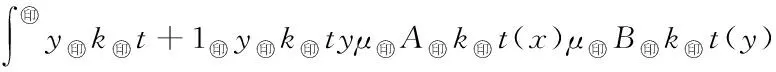










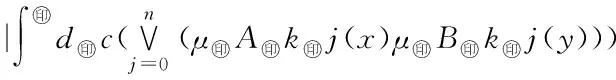












6 仿真实例


