有限域上一类对合多项式的计数

张召辉, 廖群英

(四川师范大学 数学科学学院, 四川 成都 610066)

1 序言及主要结果

鉴于对合多项式的重要性,目前已经有一部分关于对合多项式的研究.Charpin等[7]在讨论偶特征域上的Dickson多项式时,开启了关于对合多项式显性表达式及其不动点的研究.自此,人们开始关注这个问题:Charpin等[8]讨论了偶特征域上的对合单项式个数以及线性对合多项式;Castro等[9]给出Fq上的单项式在Fq上对合的充要条件,以及具有特定个数不动点的单项式在Fq上对合的充要条件;Fu等[10]证明了目前已知的四差分一致置换多项式中,大部分都不是对合多项式;Zheng等[11]利用分圆多项式的思想给出一类特殊形式的多项式是对合的充要条件;Niu等[12]基于AGW准则给出另一类特殊形式的多项式是对合的充要条件;张召辉等[13]通过讨论有限域上两个对合多项式的不动点集合与非不动点集合之间的关系,给出了两个对合多项式复合后仍然对合的充要条件等.

本文基于文献[13]给出的充要条件,在给定对合多项式f(x)∈Fq[x]的情况下,对任意g(x)∈Fq[x],通过讨论f(x)与g(x)不动点集合与非不动点集合之间的交集合,确定了使得复合函数f∘g(x)和g(x)均对合的g(x)的计数公式.

为方便,记Af表示多项式f(x)∈Fq[x]在Fq中的不动点集合.

引理 1.1[12]设f(x)∈Fq[x]为Fq上的对合多项式,|Af|=n(n∈N),则q-n为偶数.特别地,当q为奇数时,|Af|≤1.

由引理1.1可知,如果f(x)∈Fq[x]为对合多项式,则|Fq-Af|为偶数,不妨设为

|Fq-Af|=2h,h∈N,

而Fq-Af为f(x)在Fq上的非不动点集合,故可设βi=f(αi)(i=1,2,…,h),并以(αi:βi)(i=1,2,…,h)表示2-轮换(即对换).

对Fq中的对合多项式f(x),记

Bf={(α1:β1),…,(αh:βh)};

Mf={g(x)∈Fq[x]|g(x),f∘g(x)均为Fq上的对合多项式,|Af∩Ag|=|Af|,Bf⊆Bg};

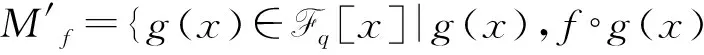
引理 1.2[13]设f1(x),f2(x)∈Fq[x]为Fq上的对合多项式,则f1∘f2(x)为Fq上的对合多项式当且仅当对任意x∈Af1,有f2(x)∈Af1,并且对(x:f1(x))∈Bf1,以下条件之一成立:

1)x,f1(x)∈Af2;

2) (x:f1(x))∈Bf2;

3) 存在(x1:x2)∈Bf1,使得(x1:x2)≠(x:f1(x)),且(x:x1),(f1(x):x2)∈Bf2.

本文利用上述充要条件,通过讨论Fq上两个对合多项式f(x)与g(x)的不动点集合与非不动点集合之间的交集合,确定了一类特殊的对合多项式的计数公式,即证明了如下主要结果.

定理 1.3设f(x)∈Fq[x]为Fq上的对合多项式,|Af|=n(n∈N),则:

1)Mf={f(x)},即|Mf|=1;

3)

其中

2 主要结果的证明

证明定理1.3.

任取g(x)∈Mf,由Bf⊆Bg可知

|Bf∩Bg|=|B

即Ag⊆Af.

因为g(x)∈Mf,所以|Af∩Ag|=|Af|,但是Ag⊆Af,从而|Af|=|Ag|=n,即Af=Ag.

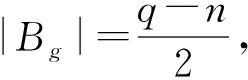
所以，由Af=Ag,Bf=Bg，可知g(x)=f(x),即Mf={f(x)},|Mf|=1.

注意到Bf⊆Bg,所以Ag⊆Af,从而

m=|Af∩Ag|=|Ag|.

因为f(x)、g(x)和f∘g(x)均为Fq上的对合多项式,所以由引理1.2可知，对任意x∈Af,有g(x)∈Af.下面对任意x0∈Af,分以下两种情形讨论.

情形 1 当x0∈Ag时,有g(x0)=x0∈Ag⊆Af.

情形 2 当x0∈Af-Ag时,由x0∉Ag可知g(x0)≠x0.

若g(x0)∈Ag,由g(x0)为Fq上的对合多项式及对合多项式的定义,易得x0∈Ag,此与x0∉Ag矛盾,故g(x0)∉Ag,即g(x0)∈Af-Ag-{x0}.

|Af∩Ag|=m, 0≤m≤n,

|Bf∩Bg|=j.

对于任意x0∈Ag,有情形3和4.

情形 3 当x0∈Af时,有x0∈Af∩Ag.

情形 4 当x0∈Fq-Af时,有(x0:f(x0))∈Bf.又x0∈Ag,故由引理1.2中1)可知f(x0)∈Ag.

又Bf中有i个2-轮换满足引理1.2中的1),|Af|=n,且|Af∩Ag|=m(0≤m≤n),故

|Ag|=m+2i.

再由引理1.1可知q-m-2i和q-n均为偶数,从而n、m与q同奇偶.

对于x0∈Fq-Ag,可知g(x0)≠x0,(x0:g(x0))∈Bg.有情形5和6.

情形 5 当f(x0)=x0时,有x0∈Af,因为x0∈Fq-Ag,所以x0∈Af-Ag,又因为f∘g(x)为Fq上的对合多项式,所以由引理1.2可知g(x0)∈Af,而g(x0)≠x0,故g(x0)∈Af-Ag-{x0}.

情形 6 当f(x0)≠x0时,有(x0:f(x0))∈Bf.

(Ⅰ) 若(x0:f(x0))=(x0:g(x0)),则f(x0)=g(x0),从而(x0:f(x0))∈Bf∩Bg.

(Ⅱ) 若(x0:f(x0))≠(x0:g(x0)),因为f∘g(x)为Fq上的对合多项式,所以,由引理1.2可知,存在(x1:x2)∈Bf,使得(x1:x2)≠(x0:f(x0)),且(x0:x1),(f(x0):x2)∈Bg.

又Bf中有2k个2-轮换满足引理1.2中的条件3),故

|B

|Af|=n,n∈N, |Af∩Ag|=m,

0≤m≤n, |Bf∩Bg|=j,

且Bf中有i个2-轮换满足引理1.2中1),2k个2-轮换满足3),则满足条件的g(x)的个数为:

事实上,不妨设

Af={al1,al2,…,alm,alm+1,…aln},

B1={(b1:f(b1)),(b2:f(b2)),…,(bi:f(bi))},

B2={(d1,1:f(d1,1),(d2,1,f(d2,1),…,

(dk,1:f(dk,1)}(当k=0时,B2=∅),

B3={(d1,2:f(d1,2)),(d2,2:f(d2,2)),…,

(dk,2:f(dk,2))}(当k=0时,B3=∅),

B4={(c1:f(c1)),(c2:f(c2)),…,(cj:f(cj))},

B当k=0时,B

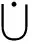
B5={(alm+e:aln+1-e)|1≤e≤n-m-1}

(当n=m时,B5=∅).

由拉格朗日插值公式可知,存在Fq上的对合多项式g(x),使得

Ag={al1,al2,…,alm,b1,f(b1),b2,f(b2),…,bi,f(bi)},

B

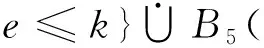
且

|Af∩Ag|=m, 0≤m≤n,

|Bf∩Bg|=j.

于是,对任意x∈Af,有g(x)∈Af,并且对(x:f(x))∈Bf,以下条件之一成立:

1)x,f(x)∈Ag;

2) (x:f(x))∈Bg;

3) 存在(x1:x2)∈Bf,使得(x1:x2)≠(x:f(x)),满足(x:x1),(f(x):x2)∈Bg.

从而,由引理1.2可知f∘g(x)为对合多项式.所以,若f(x)∈Fq[x]为Fq上的对合多项式,|Af|=n,n∈N,则

其中

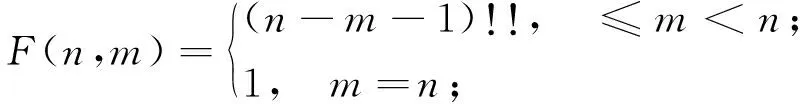
3 应用举例

本节通过实例进一步验证定理1.3.例3.1是对应于定理1.3中2)的例子,例3.2是对应于定理1.3中3)的例子.首先通过枚举法得出F7上的所有对合多项式的真值表,然后通过MATLAB利用拉格朗日插值公式得出每个真值表对应的多项式形式,其结果如附录表1～8所示.

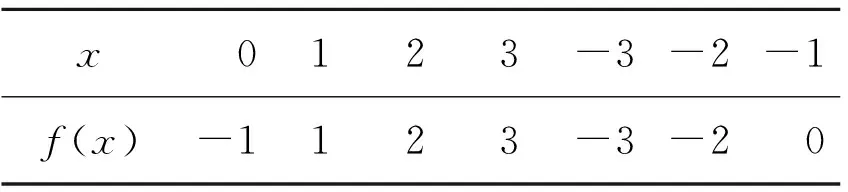
例 3.1取f(x)=x5-x4+x3-x2+2x-1∈F7[x],则f(x)的真值表如下.

x0123-3-2-1f(x)-1123-3-20

由真值表可知:f(x)为F7上的对合多项式,且

Af={1,2,3,-3,-2},

Bf={(0:-1)}.

一方面,若g(x)为F7上的对合多项式,由定理1.3的2)可知

通过枚举法将所有结果罗列出来后,再利用拉格朗日插值公式得到这些g(x),如附录表9所示,共25个.

另一方面,F7上的所有对合多项式如附录表1～8所示.经一一验证可知,仅有表9中的对合多项式与f(x)复合后仍为对合多项式.

例 3.2取f(x)=x5∈F7[x],则f(x)的真值表如下.

x0123-3-2-1f(x)01-3-223-1

由真值表可知:f(x)为F7上的对合多项式,且

Af={0,1,-1},

Bf={(2:-3),(3:-2)}.

一方面,若g(x)为F7上的对合多项式,则由定理1.3中的3)可知

通过枚举法将所有结果罗列出来后,再利用拉格朗日插值公式得到这些g(x),如附录表10所示,共24个.

另一方面,F7上的所有对合多项式如附录表1～8所示.经一一验证可知,仅有表10中的对合多项式与f(x)复合后仍为对合多项式.