正交群的新刻画①

程敏， 杨国川， 晏燕雄

1.西南大学 数学与统计学院，重庆 400715； 2.208水文地质工程地质队，重庆 400700

本文涉及的群均为有限群．clG(x)表示x在G中的共轭类，N(G)表示群G的所有共轭类类长的集合，li(G)表示群G的第i大共轭类长，特别地，

l1(G)=max{|xG|：x∈G}

设n为正整数，p为素数，π(n)表示整除n的所有互异素因子集合，特别地，π(G)=π(|G|)．Gp表示群G的某个Sylowp-子群．给定群G，G的素图Γ(G)定义为：以π(G)作为图的顶点，两顶点x，y∈π(G)有边相连当且仅当存在z∈G使得xy||z|，并记为x～y．设t(G)是Γ(G)的连通分支的个数，则

Γ(G)={πi：i=1，2，…，t(G)}

若2∈π(G)，则总假设2∈π1．其他未说明的符号和术语都是标准的(见文献[1])．

有限群的数量刻画一直是有限论研究领域的热点， 许多群论研究者都进行过相关的研究． 文献[2]讨论了一类共轭类特殊长度之集对群结构的影响． 文献[3]证明了不存在同阶交换子群个数之集为{1，2}的有限群， 并刻画了同阶交换子群个数之集为{1，3} 的群的结构． 文献[4]利用准素数子群的δ-置换性得到超可解群的若干性质．

本文继续研究群的数量性质对群结构的影响， 研究的问题与Thompson教授提出的猜想相关：

Thompson猜想设L是非交换单群，如果群G满足Z(G)=1且N(G)=N(L)， 则G≅L．

Thompson猜想指出：有限非交换单群能够被其共轭类长的集合唯一刻画． 陈贵云教授在文献[5-7]中证明了Thompson猜想对所有素图不连通的有限非交换单群成立．文献[8]减弱了Thompson猜想的条件， 用群的阶与某些共轭类长刻画了散在单群和单K3-群． 文献[9]用群的阶以及某些特殊共轭类长刻画了单K4-群． 文献[10-12]用群的阶以及某些特殊共轭类长刻画了Ap，Cn(2)及Sp+1等．

本文继续这一研究， 主要结果如下：

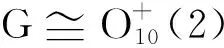
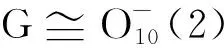
定理1的证明

必要性是显然的，下面只证充分性．

由文献[1]知

l5(G)=220·35·52·7·17

因此G存在31阶元x， 使得CG(x)=〈x〉． 于是，{31}是群G的一个素图分支， 即t(G)≥2．

下面先证明：G既不是Frobenius群又不是2-Frobenius群．

断言：G不是Frobenius群．

否则，设G是以H为核，K为补的Frobenius群． 由文献[13]的引理2.6(1)知t(G)=2．

如果31∈π(H)，则

π(K)={2，3，5，7，17}

|K|=220·35·52·7·17

从而220·35·52·7·17|30，矛盾．

如果31∈π(K)，则

π(H)={2，3，5，7，17}

|H|=220·35·52·7·17

设H7∈Syl7(H)，由H幂零得H7◁_G，且由文献[14]的定理4.5.3得|Aut(H7)|=6．则

(31，|Aut(H7)|)=1

由文献[9]的引理2.12得7～31， 矛盾．

再证明：G不是2-Frobenius群．

如果G是2-Frobenius群，则由文献[15]的定理2得t(G)=2．此时G有一正规群列1◁_H◁_K◁_G， 使得

π(K/H)=π2π(H)∪π(G/K)=π1

且|G/K|||Aut(K/H)|．由于t(G)=2，且{31}是群G的一个素图分支， 则

π2=π(K/H)={31}

从而|G/K||30，且7∈π(H)．设H7∈Syl7(H)，由H幂零得H7◁_G，且|Aut(H7)|=6．于是

(31，|Aut(H7)|)=1

且7～31，矛盾．

因此，G既不是一个Frobenius群，又不是一个2-Frobenius群．

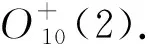
若K/H≅L2(31)，L5(2)，则|Out(K/H)|=2． 由|G/K|||Out(K/H)|得17∈π(H)．设H17∈Syl17(H)，则H17◁_G．由于

(31，|Aut(H17)|)=1

由文献[9]的引理2.12得17～31，矛盾．

定理2的证明

必要性是显然的，下面只证充分性．

由定理的条件知

l1(G)=220·36·52·7·11

因此G中存在17阶元y，使得CG(y)=〈y〉，则{17}是群G的一个素图分支，且t(G)≥2．

断言：G不是Frobenius群．

否则，设G是以H为核，K为补的Frobenius群．由文献[13]的引理2.6(1)知：

如果17∈π(H)，则

π(K)={2，3，5，7，11}

|K|=220·36·52·7·11

从而220·36·52·7·11|16，矛盾．

如果17∈π(K)，则

π(H)={2，3，5，7，11}

且

|H|=220·36·52·7·11

设H11∈Syl11(H)，由H幂零及文献[14]的定理4.5.3得

H11◁_G|Aut(H11)|=10

于是(17，|Aut(H11)|)=1． 由文献[9]的引理2.12得17～11，矛盾．

再证明：G不是2-Frobenius群．

否则，由G是2-Frobenius群及文献[15]的定理2知t(G)=2．此时G有一正规群列1◁_H◁_K◁_G， 使得

π(K/H)=π2π(H)∪π(G/K)=π1

且|G/K|||Aut(K/H)|．由于t(G)=2，且{17}是群G的一个素图分支， 则

π2=π(K/H)={17}

从而|G/K||16且11∈π(H)．设H11∈Syl11(H)，由H幂零得H11◁_G且|Aut(H11)|=10．进一步，有17～11，矛盾．

从而，G既不是Frobenius群，又不是2-Frobenius群．

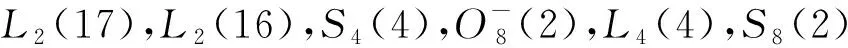
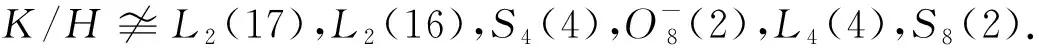
否则，由于11∉π(K/H)，且|Out(K/H)|=2n(n≤2)，得11∈π(H)．设H11∈Syl11(H)，则H11◁_G．因为

(17，|Aut(H11)|)=1

所以由文献[9]的引理2.12得17～11，矛盾．