罗茨转子具有节弦高内共轭段的高能轮廓构造
2022-03-24李玉龙张安民
刘 萍,李玉龙,张安民,赵 岩
(宿迁学院,江苏宿迁 223800)
0 引言
罗茨泵是利用2个相同罗茨转子共轭旋转中所产生的进口真空吸力,将流体介质输送到出口的一类容积设备[1],随着其在空天海洋装备中的逐步运用[2],相应的轻量化要求也越来越高[3-5]。研究表明“泵容积效率≈转子容积利用系数×(100%-内泄漏率)”决定了泵的轻量化程度[6],其中,容积利用系数越大和内泄漏率越小,容积效率就越高,轻量化程度就越好;容积利用系数=“转子顶圆柱体积中用于挤出介质的部分叶槽容积/转子顶圆柱的体积”≈“1-1/转子形状系数的平方”[7];内泄漏率≈径向泄漏率+轴向泄漏率+共轭泄漏率[6]。因此在转子的轮廓设计中,总希望通过采用最大化的形状系数和最小化的内泄漏控制措施,以期获得更高的容积效率和更好的轻量化效果[8-9]。目前,在常见渐开线、摆线、圆弧等转子中,圆弧转子所具有2叶的1.670、3叶的1.477、4叶的1.368为已知最大形状系数[6],能否进一步提高该最大形状系数呢?为此,拟就所期望的更大形状系数和更小内泄漏率,提出一种由转子半叶节圆弧的弦高线(简称为节弦高)为节圆内共轭轮廓段的特殊构造方法,并就其高形化技术的应用展开进一步研究。
1 转子形状系数对共轭轮廓段形状的影响
对于叶顶叶谷均采用圆弧过渡的普通转子[10],其形状系数的大小由转子轮廓中的共轭段形状直接决定,且共轭段由(节圆)外共轭段和(节圆)内共轭段两部分组成。以3叶渐开线普通转子的半叶轮廓为例,ε0=1.20,1.35,1.46三种普通转子形状系数下的外共轭段12和内共轭段23,如图1所示。其中,ε0=1.46为渐开线普通转子的上限形状系数[11],o为转子中心,顶 op、谷轴 ov分别为转子叶顶部、谷部的对称轴,简称为顶轴、谷轴;顶轴、谷轴的平分轴为中轴o2,顶轴与节圆的交点为顶节点a,谷轴与节圆的交点为谷节点b。
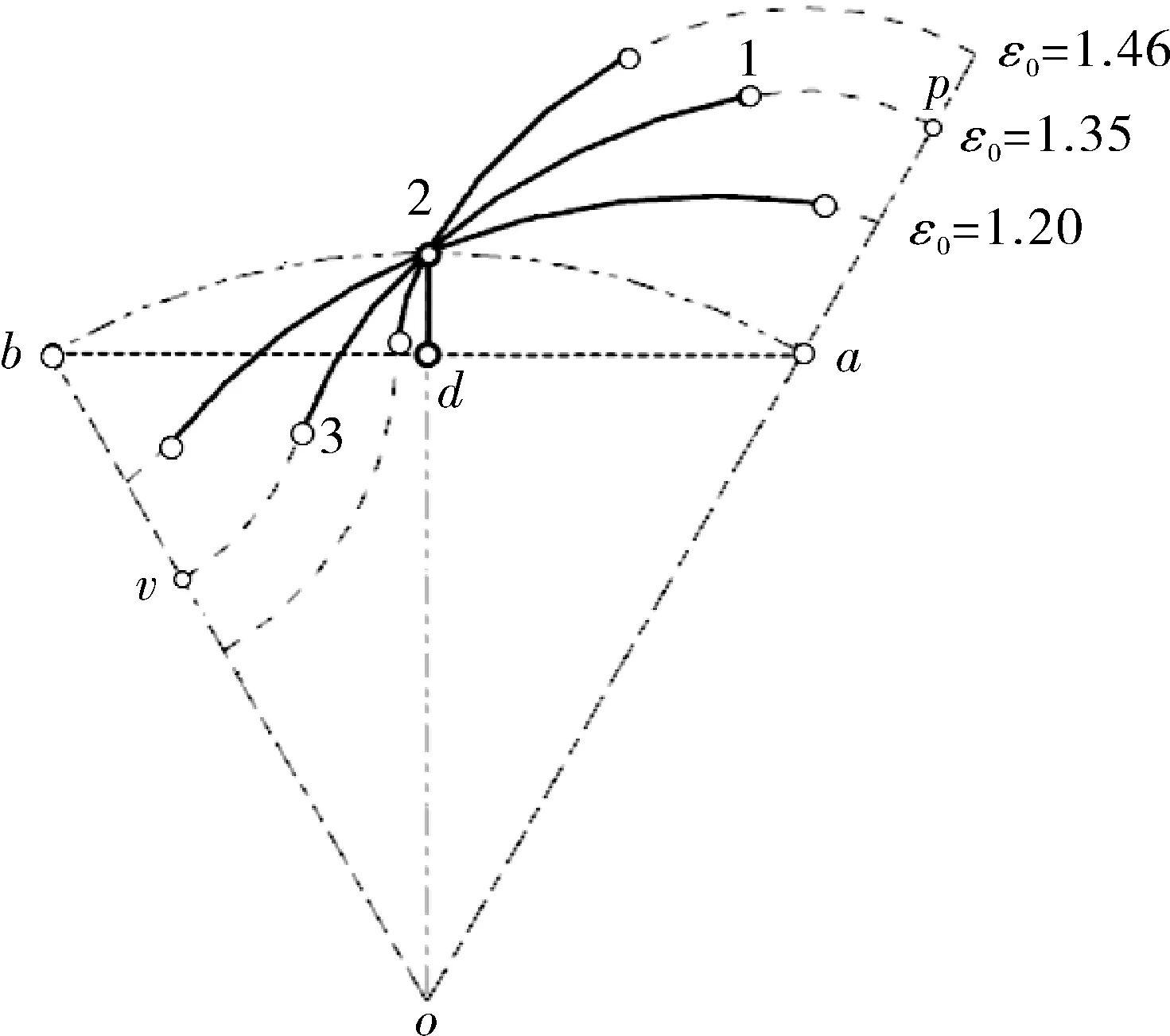
图1 形状系数对共轭轮廓段形状的影响Fig.1 Influence of shape coefficient on the shape of conjugate profile segment
由3种普通转子形状系数ε0下12+23段曲线的形状变化,知ε0越大,23段具有逐步贴近半叶节圆弧ab弦高2d的变化趋势,则当23段采用该弦高时,对应的转子称为节弦高内共轭普通转子,该转子理应取得比3叶渐开线普通转子1.46的上限形状系数的更大形状系数,且节弦高的平-凸共轭模式较渐开线的凸-凸模式,更利于抑制共轭泄漏[3]。
2 转子共轭轮廓段上的双对称几何关系
图2中,设点6,7为节圆上关于中轴互为对称的2个点,对应的圆心角均为(2N),N为转子叶数,点6,7在段12,23上的法向垂足为轮廓点4,5。
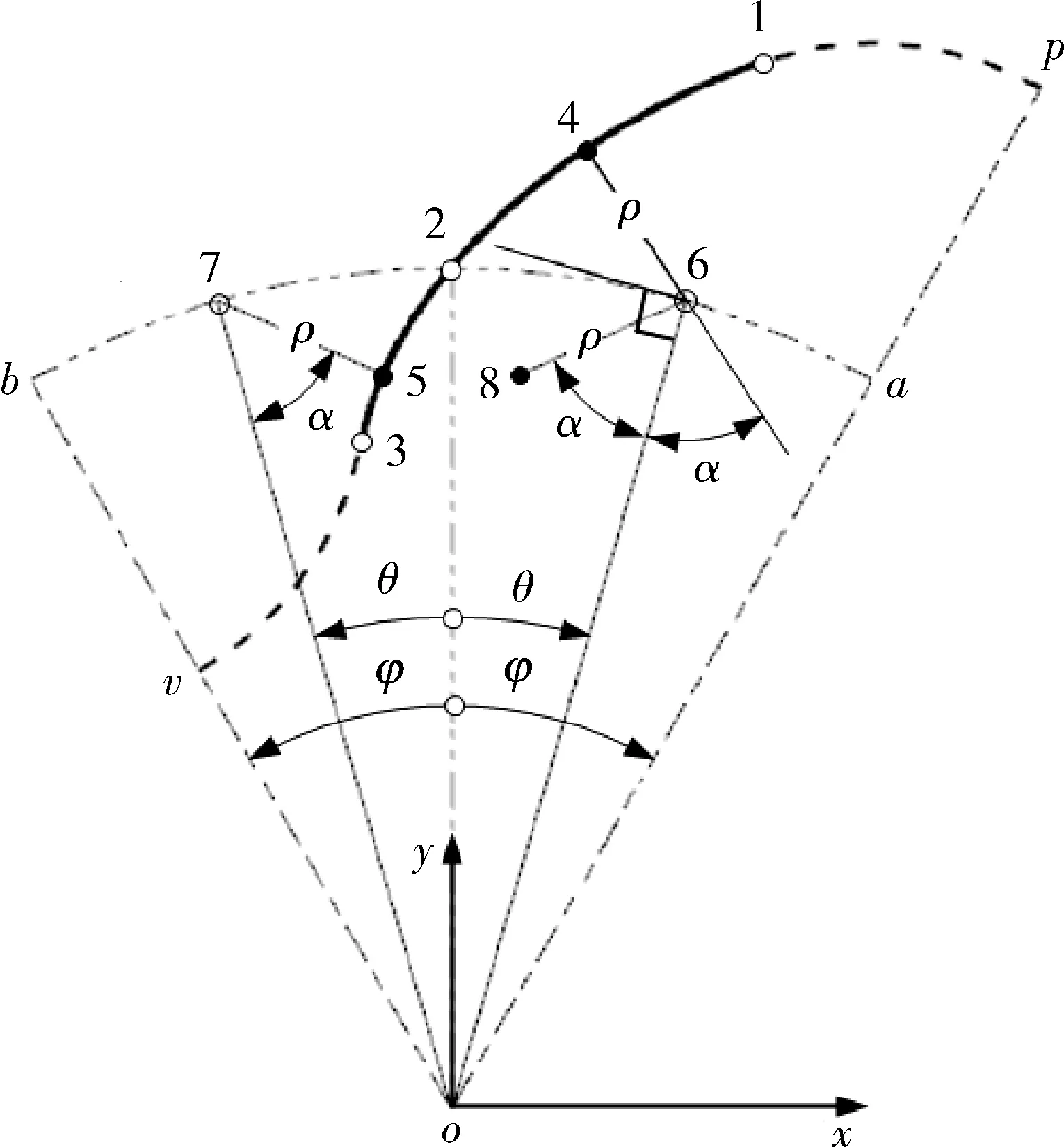
图2 共轭轮廓段间的双对称几何关系Fig.2 Double symmetric geometric relations between conjugate profile segments
由两相同转子间的共轭原理[10],知轮廓线46,57具有相同的瞬径ρ(θ),线46与线 6o间、线57与线7o间具有相同的瞬角α(θ),即点6,7为点4,5的共轭瞬心,及线46与线86关于点6处节圆切线对称、线86与线57关于中轴对称,或者说外共轭瞬径46/外共轭段12与内共轭瞬径57/内共轭段23间具有一种互为双对称的几何关系。则由其中任一确定的共轭段,透过彼此间的双对称几何关系,能求出另一待定的共轭段。
为此,在图2示出的xoy坐标系下,外共轭段12和内共轭段23的规律曲线方程为:
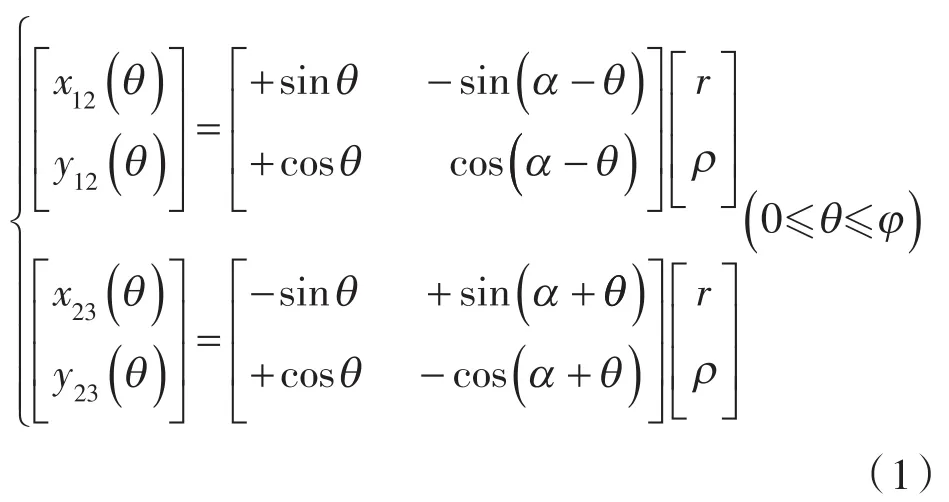
式中 r ——节圆半径。
3 普通转子的形状系数及其轮廓构造
对于节弦高内共轭普通转子的轮廓,其内共轭段23为确定段,外共轭段12为待求段。由图3所示节弦高23的位置关系,得:
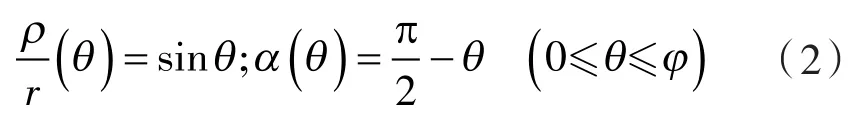
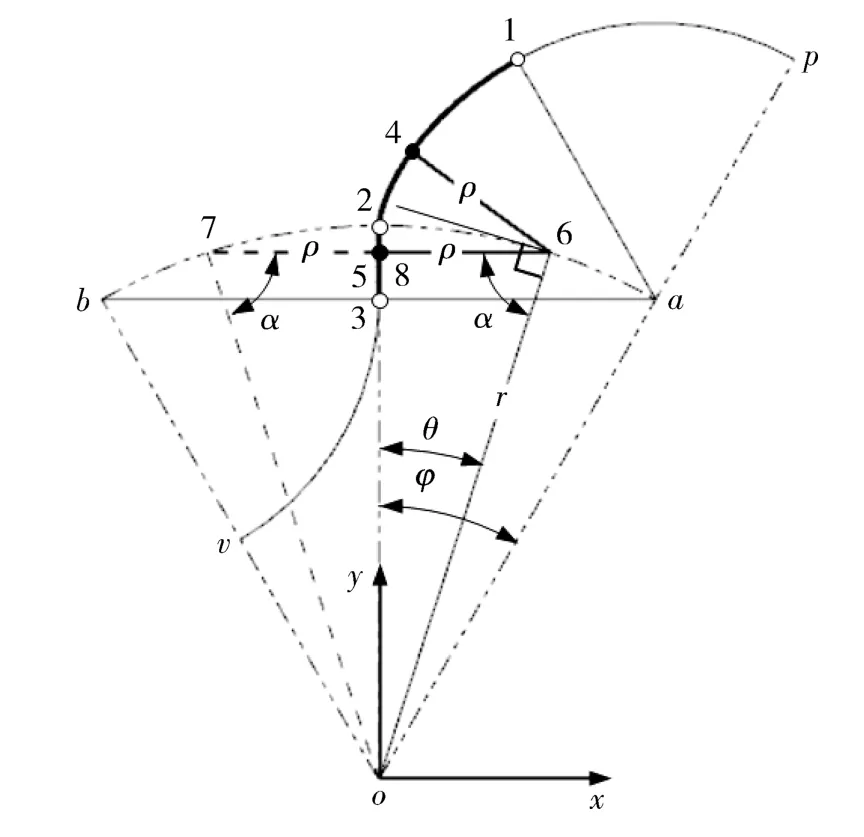
图3 节弦高内共轭转子的普通轮廓构造Fig.3 Ordinary-profile structure of conjugate rotor with chord height of pitch arc as inner conjugate profile segment
并由式(1),得外共轭段12的规律曲线方程为:
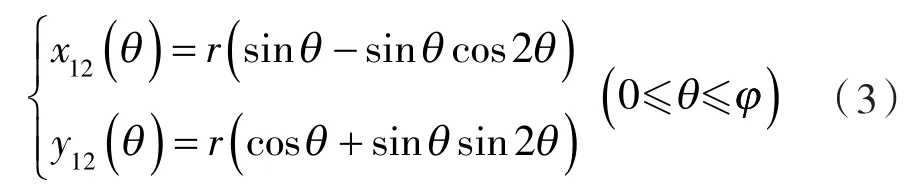
其次,由θ=φ,得节弦高内共轭普通转子的形状系数ε0为:
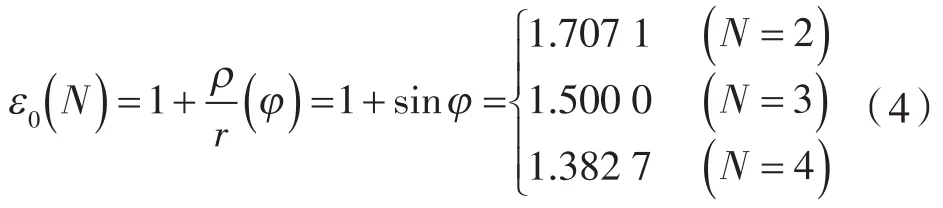
最后,将式(2)所给出的 ρ/r和式(4)所给出的ε0代入下式(容积利用系数式)[7]:
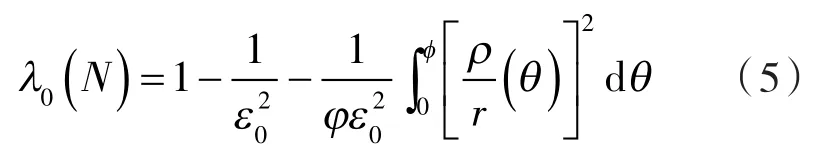
得节弦高内共轭普通转子的容积利用系数λ0为:
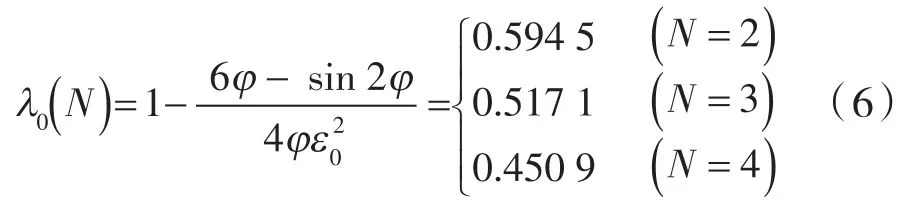
3叶节弦高内共轭普通转子副的3D模型及其相关几何量的测量,如图4所示。其中,3D模型由UGNX软件依据式(1)(2)绘制,节圆半径取为r=100 mm,由3D模型测量出的叶顶半径为ra=150 mm,转子端面的面积为A=34 133.440 3 mm2且转子副无啮合余隙。
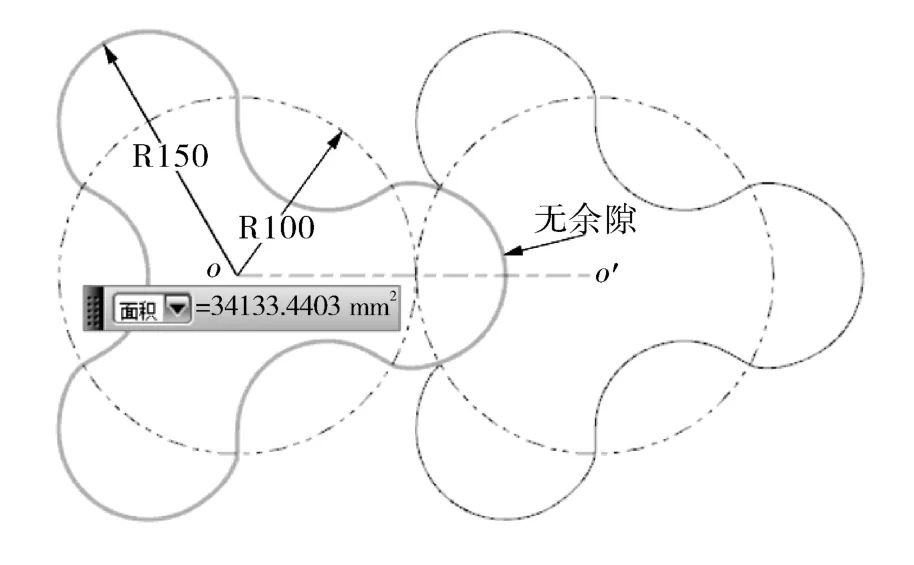
图4 3叶节弦高内共轭普通转子副及其测量Fig.4 3-lobe ordinary-profile rotor pairs with chord height of pitch arc as inner conjugate profile segment and area measurement
3叶节弦高内共轭普通转子的验证形状系数为ra/r=150/100=1.5,与式(4)给出的理论形状系数完全一致,且由验证容积利用系数计算式(式(7))计算结果与式(6)给出的理论容积利用系数完全一致,说明节弦高内共轭普通转子的ε0式(4)和λ0式(6)正确。
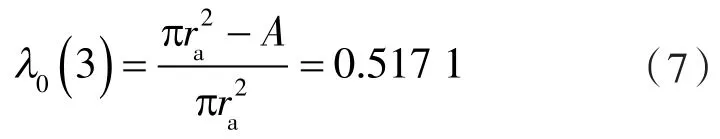
与具有已知最大上限形状系数和上限容积利用系数的圆弧普通转子[11](式(8))相比,2,3,4叶节弦高内共轭普通转子的形状系数提高了2.23%,1.56%和1.07%,容积利用系数提高了2.29%,2.70%和2.55%,且加工相对简单。
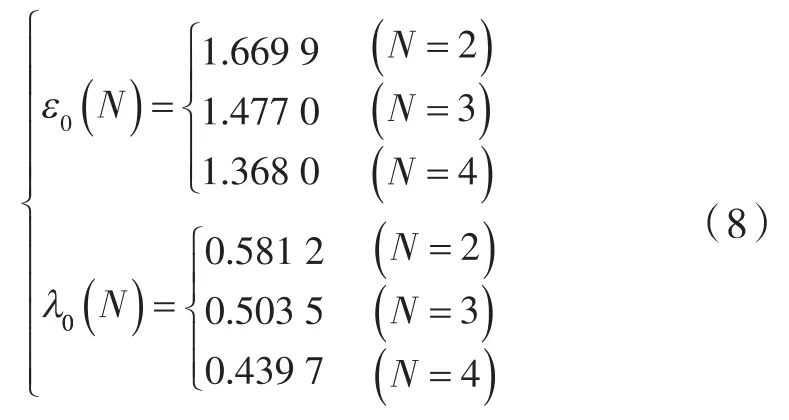
4 高形转子的形状系数及其轮廓构造
为充分控制节弦高内共轭普通转子的叶顶径向泄漏和缓解排气侧压缩反冲现象对该径向泄漏的影响[12],可采用如图5所示的节弦高内共轭高形构造[13]。其中,顶mp、谷nv圆弧的圆心均为转子中心o,半径分别为rε、(2-ε)r,圆心角均为顶封角γ,ε为高形转子的形状系数,即ε=mo的连线长度lmo/节圆半径r。
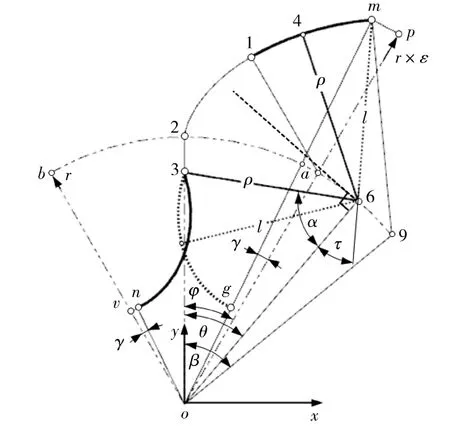
图5 节弦高内共轭转子的高形轮廓构造Fig.5 Tall-profile structure of conjugate rotor with chord height of pitch arc as inner conjugate profile segment
由于顶圆弧mp与泵壳腔内圆弧面具有转子中心o的共同圆心,所以叶顶间隙为径向等缝隙,较普通转子的径向凸-凹缝隙,能有效降低径向泄漏。
图5中,取对应于β>φ的节圆点9,则三角形△mo9中的角∠mo9=β-φ+γ,由前述双对称几何关系知边长m9的长度lm9为点3,9的连线长度l39,角∠m9o=π-∠39o;三角形△3o9中的边长o3的长度lo3=rcosφ。
在三角形△3o9中,由三角形几何关系,得:
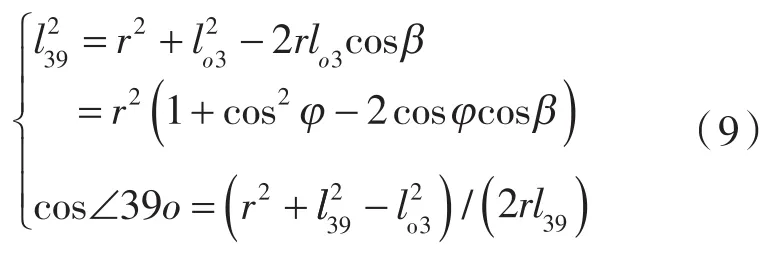
在三角形△mo9中,由三角形几何关系,lm9=l39,∠m9o=π -∠39o 及lo3=rcosφ,得mo的连线长度lmo为:
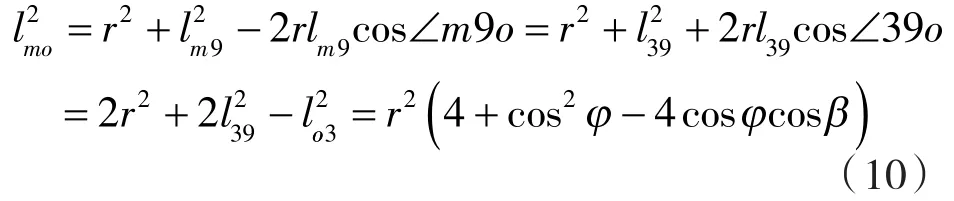
则节弦高内共轭高形转子的形状系数ε为:
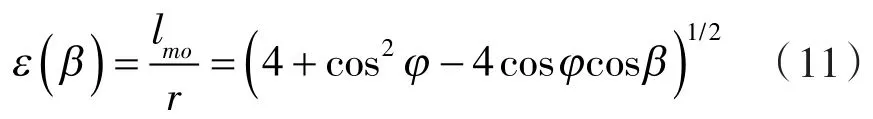
及节弦高内共轭高形转子的容积利用系数λ为:
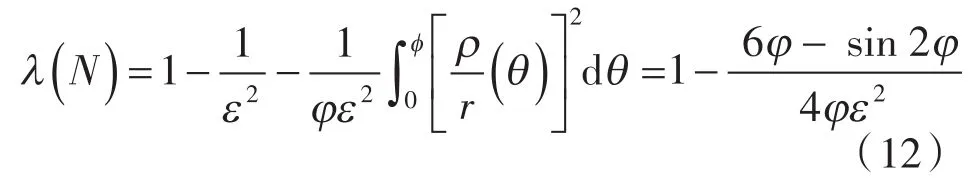
由m9的长度lm9=l39,角∠m9o=π -∠39o,及三角形△mo9中的:
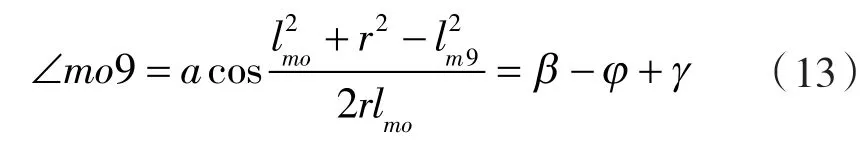
得节弦高内共轭高形转子的顶封角γ为:
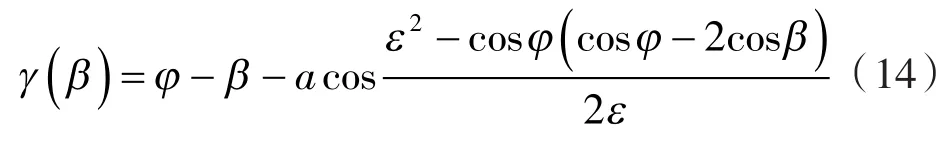
N=3下ε(β)、γ(β)、λ(β)的变化规律,见表1。以3叶β=50.8°的节弦高内共轭高形转子为例,此时ε=1.60、λ=0.57,针对其普通转子的ε0=1.50、λ0=0.517 1,ε提高了 6.67%,λ提高了10.03%。针对与具有已知最大上限形状系数1.477和上限容积利用系数0.503 5的圆弧普通转子,ε提高了8.33%,λ提高了13.21%。
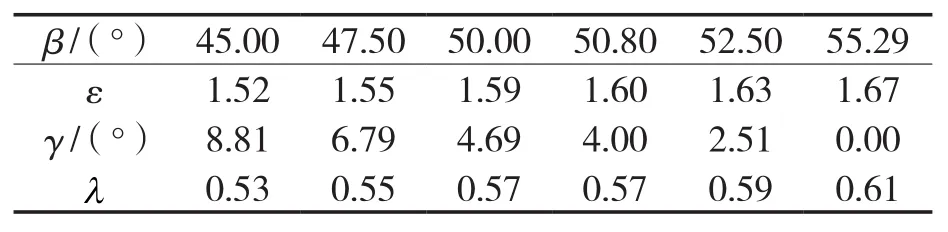
表1 3叶高形转子的形状系数和顶封角及容积利用系数Tab.1 Shape coefficient, top sealing angle and volume utilization coefficient of 3-lobe tall-profile rotor
当θ位于[φ,β]区间内时,采用双对称构造方法,得与点3共轭的(节圆)外轮廓段1 m的规律曲线方程为:
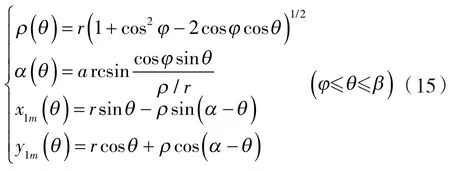
式中 ρ(θ)——图5中线段36的长度;
α(θ)——线段36与线段6o的夹角。
当θ位于[φ-γ,β]区间内时,采用双对称构造方法,得与点m共轭的(节圆)内轮廓段3n的规律曲线方程为:
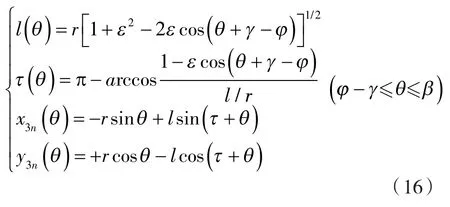
式中 l(θ)——图5中线段6m的长度;
τ(θ)——图5中线段6m与线段6o的夹角。
3叶节弦高内共轭高形转子副的3D模型及其相关几何量的测量,如图6所示。其中,β取50.80°,节圆半径r=100 mm,由3D模型测量出的的叶顶半径ra=160 mm,顶封角γ=4°,转子端面面积A=33 255.964 2 mm2,半叶余隙面积 185.547 5 mm2。则,全叶余隙面积为S=1 113.285 mm2,3叶节弦高内共轭转子的高形验证形状系数为ra/r=160/100=1.6,且由其高形验证容积利用系数计算式(式(7))所得结果及顶封角均与表1给出的对应理论值完全一致,说明节弦高内共轭高形转子的式(11)、式(12)、式(14)及轮廓构造式(15)(16)正确。
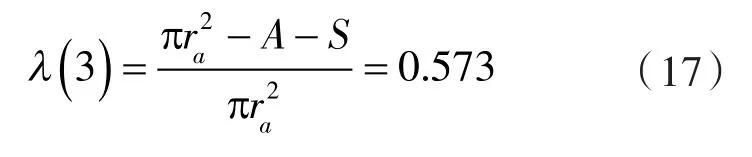
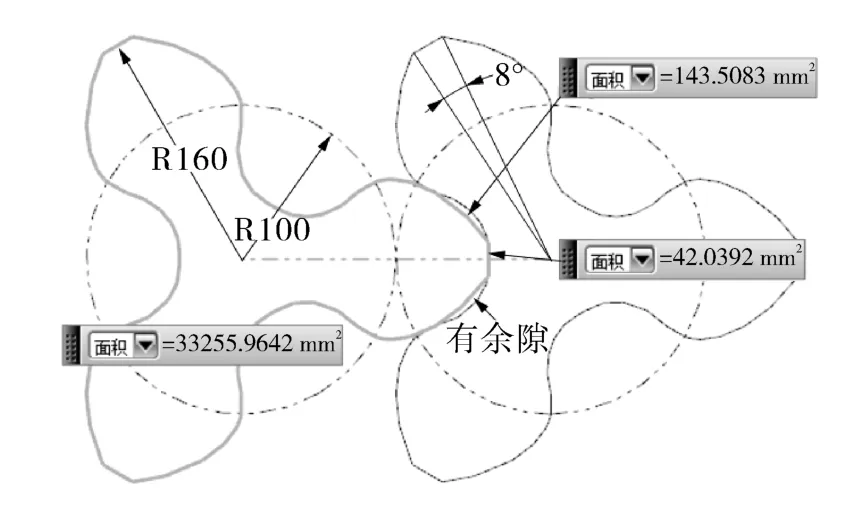
图6 3叶节弦高内共轭高形转子副及其面积测量Fig.6 3-lobe tall-profile rotor pairs with chord height of pitch arc as inner conjugate profile segment and area measurement
5 普通转子与高形转子的优劣比较
从泵轻量化效果所涉及的形状系数和内泄漏看,高形转子因径向泄漏率小于、形状系数大于普通转子,故高形转子更利于取得最大化的形状系数和最小化的径向泄漏。同时,高形转子副在不同的旋转区间内,将会出现不同的共轭/密封点位。设ω为旋转角,则0≤ω<γ内将有5个,ω=γ有4个,γ≤ω<β-φ有3个(如图7所示),ω=β-φ有2个,β-φ≤ω<φ内有1个的不同共轭/密封点位数。
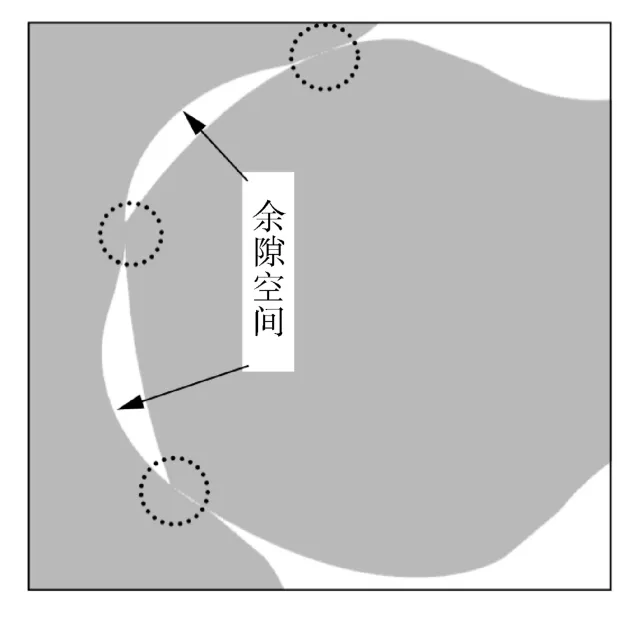
图7 高形转子副不同区间内的密封点位数Fig.7 Number of sealing points in different rotating intervals of tall-profile rotor pairs
以 3叶 β=50.8°为例,相对于 0< ω <φ内仅有1个共轭/密封点位的普通转子副,多点位共轭/密封区间占比 β/φ-1=69.33%,因此共轭泄漏更小。
由于罗茨转子泵多为非高速流体介质,转子间也存在较大非接触间隙,所以共轭区多点位共轭/密封不会形成类似齿轮泵的困油现象,或者这种现象很轻微。
但高形转子副存在一定的余隙空间,其内的高压出口介质会随着转子副的旋转而回流到泵的低压进口腔,从而影响到象罗茨真空泵进口腔内介质的真空度质量,故罗茨真空泵不建议使用高形转子副。
6 结论
(1)内共轭轮廓段采用节弦高的普通转子,具有比圆弧转子更大的形状系数和容积利用系数。
(2)内共轭轮廓段采用节弦高的高形转子,将进一步获得更大的形状系数和容积利用系数。
(3)高形转子副的2~5个多共轭/密封的点位数及高达69.33%区间占比,加上平-凸共轭模式的自身优势,使共轭泄漏最小化,径向等缝隙密封使径向泄漏最小化。
