凸转子定点共轭的极限轮廓构造及轻量化分析
2022-09-21陈曦刘嘉
陈曦,刘嘉
(1.重庆化工职业学院,重庆 401220;2.太原工业学院机械工程系,山西太原 030008)
0 前言
凸转子泵是利用两个相同凸转子在旋转过程中所产生的进口真空吸力,将介质输送到出口的一类容积泵,应用广泛。其中,转子副广义上分为接触式(如齿轮泵)和非接触式(如罗茨泵)两类,转子的容积利用系数是衡量该类泵轻量化效果、流量脉动性能的最重要指标之一,如形状系数越大,容积利用系数(≈1-1/)越大,泵的单位体积排量就越大,额定排量下的“转子体积/质量∝1/”就越低,即轻量化效果越好。对于具有顶偏心圆弧过渡的常见普通转子,其形状系数由转子轮廓中共轭段的形状直接决定。其中,共轭段由节圆外共轭段和节圆内共轭段两部分组成;由普通转子经高形化改进后得到的高形转子,其转子形状系数可进一步提高。针对共轭段所采用的不同曲线类型,目前虽然已有各自最大形状系数的通用判据及计算方法,但是并没有解决共轭段为何曲线类型时能取得所有曲线类型中的极限形状系数问题。为此,旨在由内共轭段收缩为一定点时的轮廓构造条件,直接计算出转子能取得的该极限形状系数,并由此确定出外共轭段的曲线方程,并针对其高形化应用作进一步研究。
1 内外共轭段形状随形状系数的变化规律
在现有普通转子中,渐开线转子具有较大的形状系数。以三叶渐开线普通转子为例,1.20、1.35、1.46三种形状系数下的半叶外共轭段和内共轭段,如图1中的Ⅰ、Ⅱ、Ⅲ所示。其中,其极限形状系数为1.46,由于渐开线构造原理上的特殊性,外共轭段和内共轭段为一条完整的渐开线段。
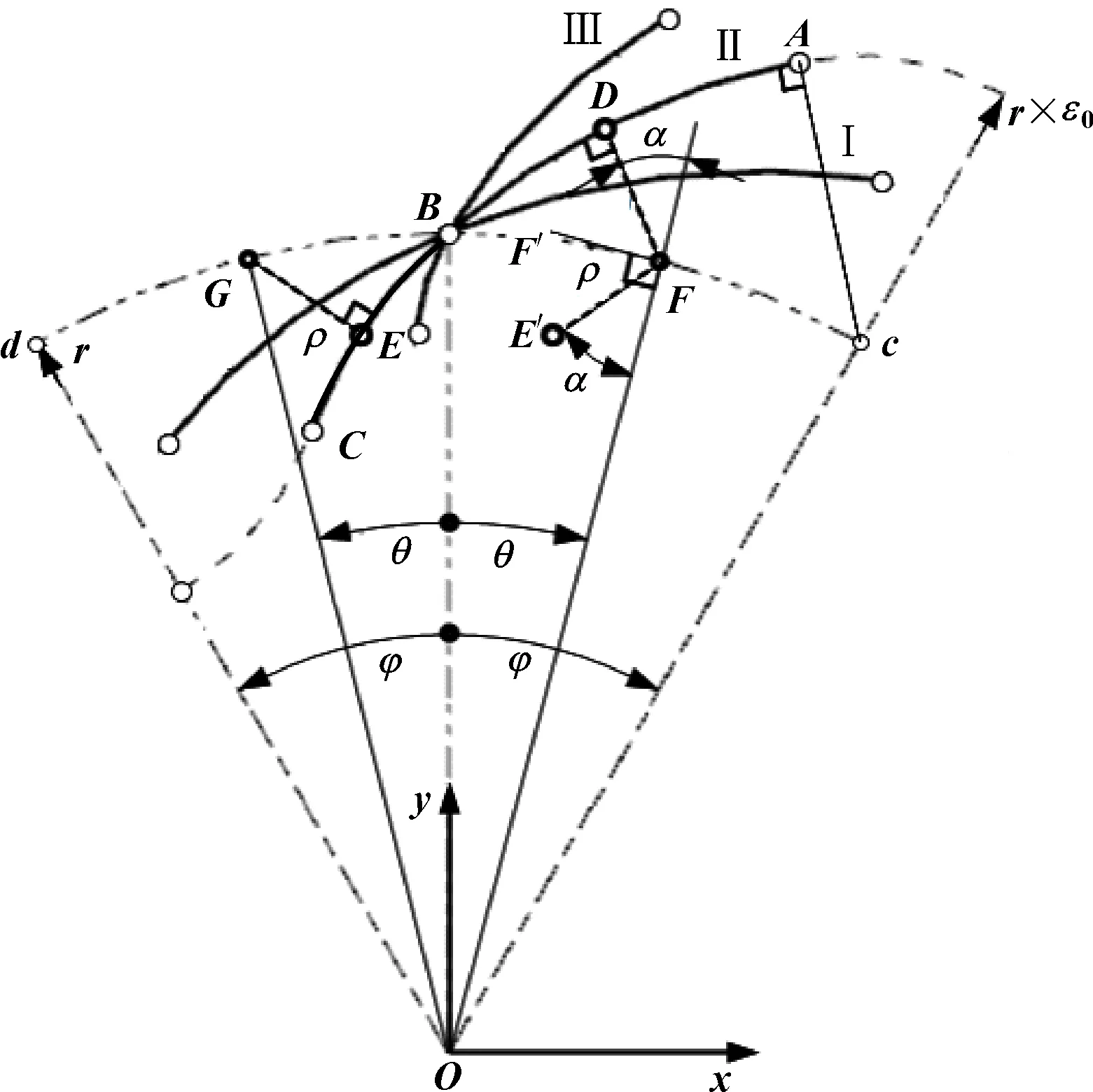
图1 共轭轮廓段间的双对称关系
设转子中心为,节圆半径为,转子叶的峰、谷对称轴与节圆的交点分别为峰节点、谷节点,间节圆弧的圆心角为2=π/,为转子叶数,中轴为峰、谷对称轴间的角平分轴,且中轴过节点,叶顶部、谷部采用圆心为峰节点、谷节点的过渡圆弧段,即为最常见的普通转子。此时转子顶过渡圆弧面(圆心非)与泵壳内腔圆弧面(圆心为)形成的径向间隙为非等间隙,径向泄漏较大。
图1中,设点、为节圆上关于中轴对称的2个点,对应圆心角为,0≤≤,点、在渐开线段上的法向垂足分别为点、。
由两相同转子间的共轭原理,知、的连线具有相同的长度,设为();连线与连线间、连线与连线间具有相同的夹角,设为()。
此时显然连线关于中轴的对称线为′连线;连线关于节圆切线′的对称线也为′连线,即连线和连线具有先关于点处节圆切线互为对称和后关于中轴互为对称的几何关系。利用这种关系的轮廓构造方法称为双对称构造法,如图1所示。
在图1所示坐标系下,外共轭段和内共轭段的坐标方程(0≤≤)分别为
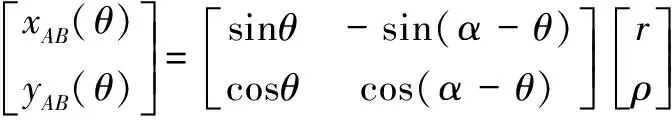
(1)
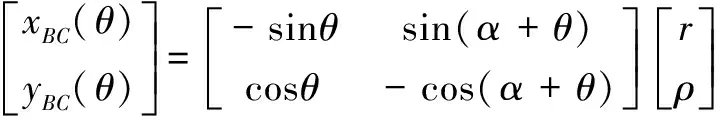
(2)
式中:(,)、(,)分别为图1中外共轭段、内共轭段上点、点的坐标。
由外共轭段和内共轭段在1.20、1.35、1.46三种形状系数下的变化规律,知越大,内共轭段向节点逐步收缩聚集的趋势越大,当收缩汇聚为节点时,称之为定点共轭。相应地,应取得普通转子各种曲线类型下的极限形状系数,否则,将因内共轭段位于节圆外,不能形成转子副正确的共轭几何关系,如图2所示。
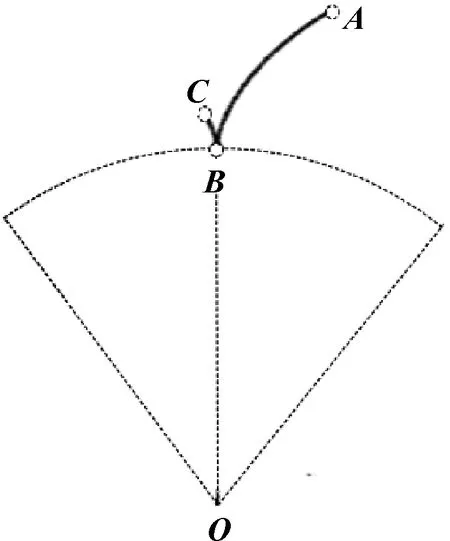
图2 内共轭轮廓段的几何干涉
2 定点共轭普通转子的轮廓构造及形状系数
图1中当内共轭段收缩汇聚为节点时,对应的普通转子半叶轮廓如图3所示。此时,由等腰△的几何关系得:
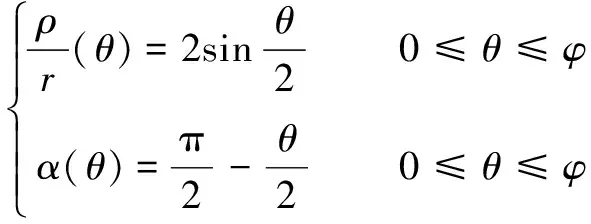
(3)
将式(3)代入式(1),则外共轭段在图3所示下的坐标方程为
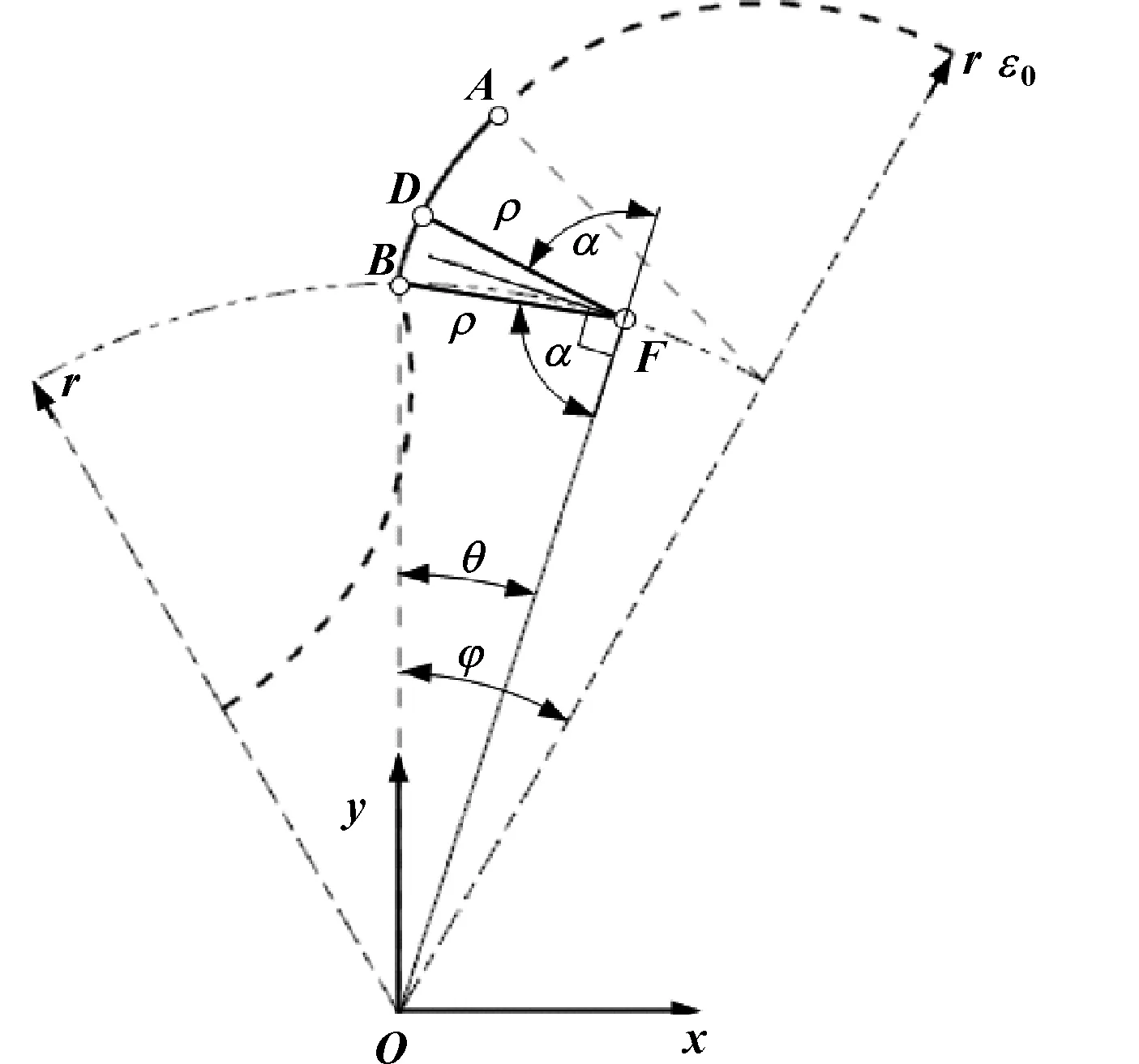
图3 定点共轭普通转子的轮廓构造
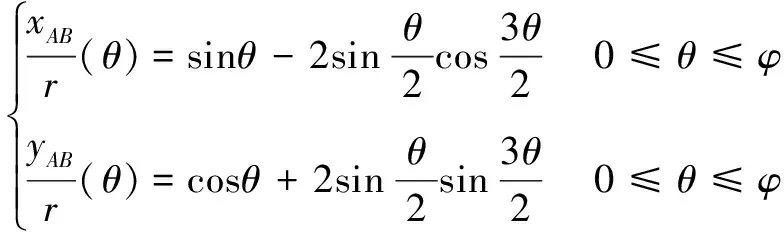
(4)
将=代入式(3),得定点共轭普通转子的形状系数为
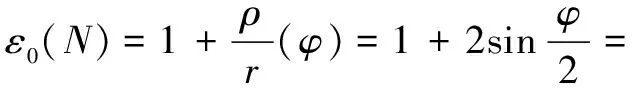
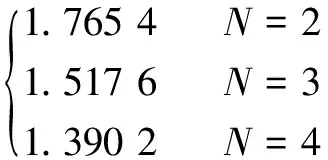
(5)
由文献[12]容积利用系数计算式的进一步推导,得定点共轭普通转子的容积利用系数为
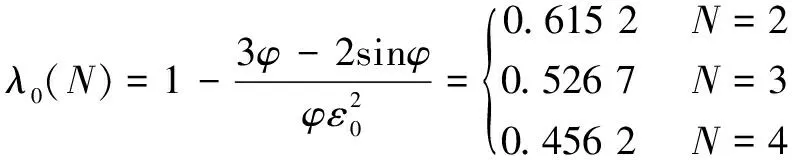
(6)
三叶下的验证如图4所示。其中,验证采用UGNX软件中的面积测量工具。
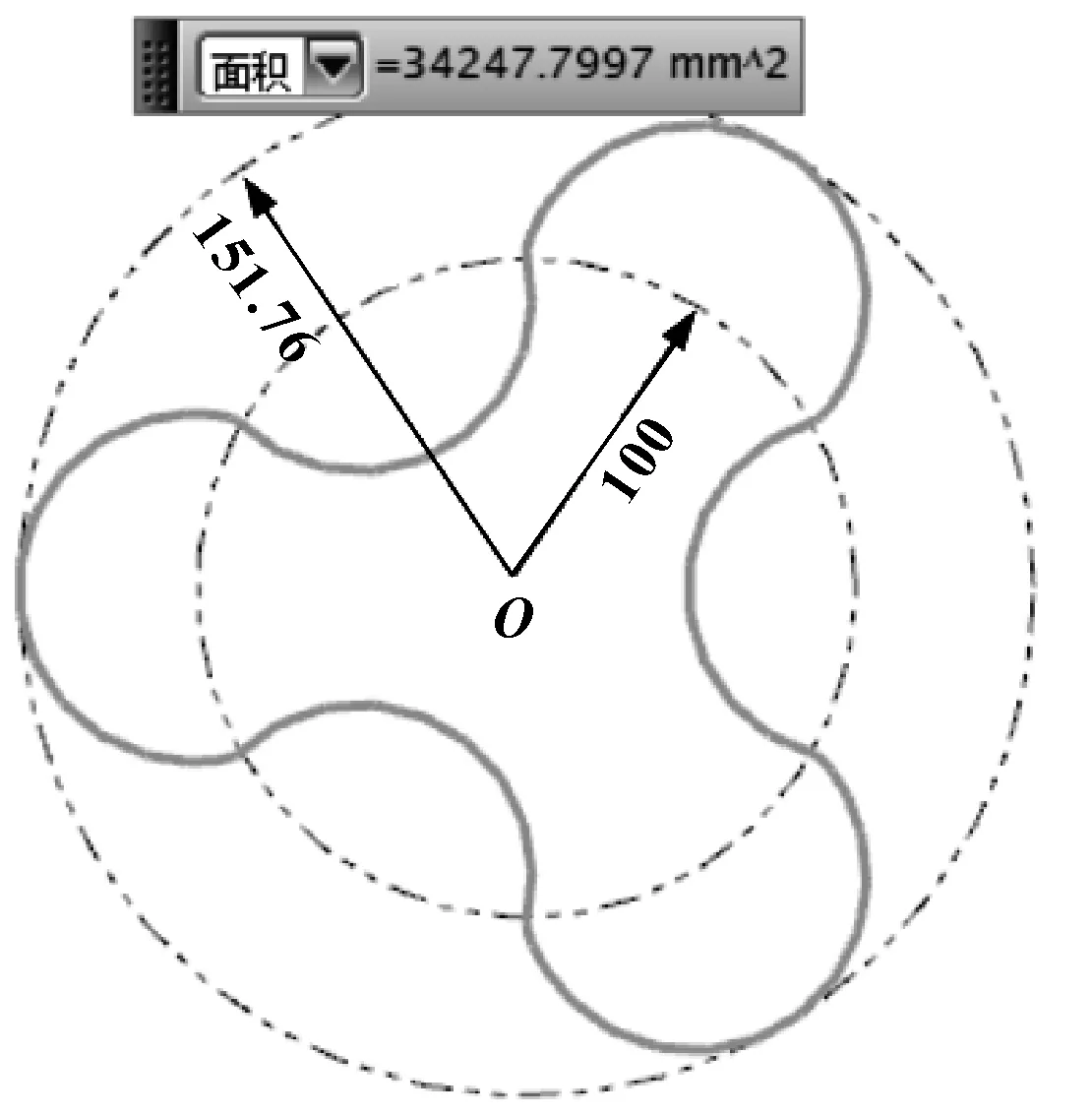
图4 三叶定点共轭普通转子模型
由图4测量出:
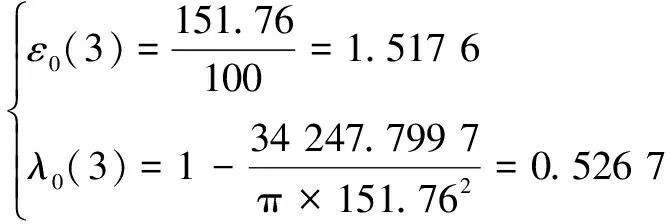
(7)
式(7)结果与式(5)—式(6)完全一致,说明式(1)—式(6)正确。
渐开线普通转子的最大形状系数及其最大容积利用系数分别为
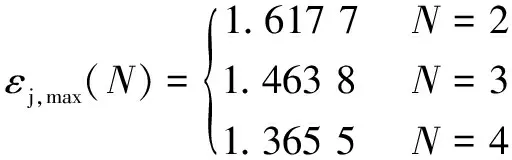
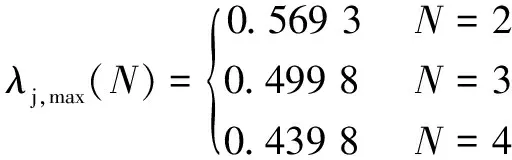
(8)
由式(8)知二、三、四叶定点共轭普通转子的形状系数与普通转子相比分别提高了9.13%、3.68%和1.81%,容积利用系数分别提高了8.06%、5.38%和3.72%。
3 定点共轭高形转子的轮廓构造及形状系数
为充分控制定点共轭普通转子顶部的径向泄漏和缓解排气侧压缩反冲现象对该径向泄漏的影响,可采用如图5所示的定点共轭结合顶同心圆弧段的高形轮廓构造,与相共轭的谷圆弧段为。其中,顶同心圆弧段、谷圆弧段的圆心均为转子中心,半径为、(2-),圆心角均为顶封角,因能大幅度提高普通转子的形状系数,故称之为定点共轭高形转子。

图5 定点共轭高形转子的轮廓构造
图5中,取对应于>的节圆点为,并由控制的变化上限。
根据等腰△的三角几何关系,边的长度和角∠分别为
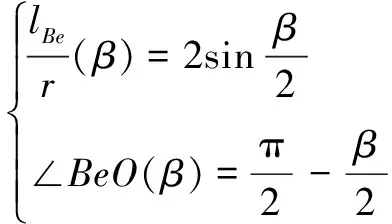
(9)
由△中的几何关系,得边的长度和角∠分别为
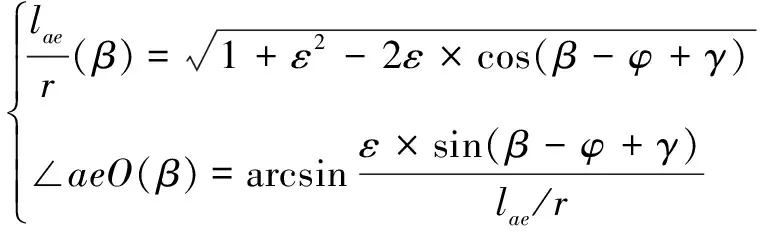
(10)
由转子与配对转子完全相同和转子副旋转过程中的轮廓点恰好避让配对转子上的轮廓点的轮廓构造,得=及∠=π-2∠,即∠=∠+ ∠=π-∠。
联立式(9)和(10),得定点共轭高形转子的形状系数和顶封角分别为
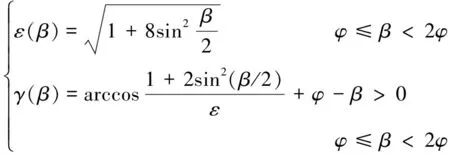
(11)
再由容积利用系数计算式进一步推导,得定点共轭高形转子的容积利用系数为
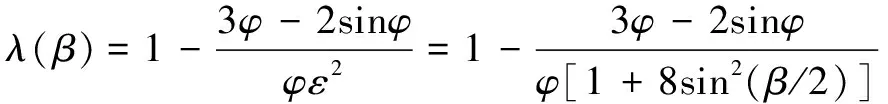
(12)
其中,=3下()、()、()的变化规律如表1所示。
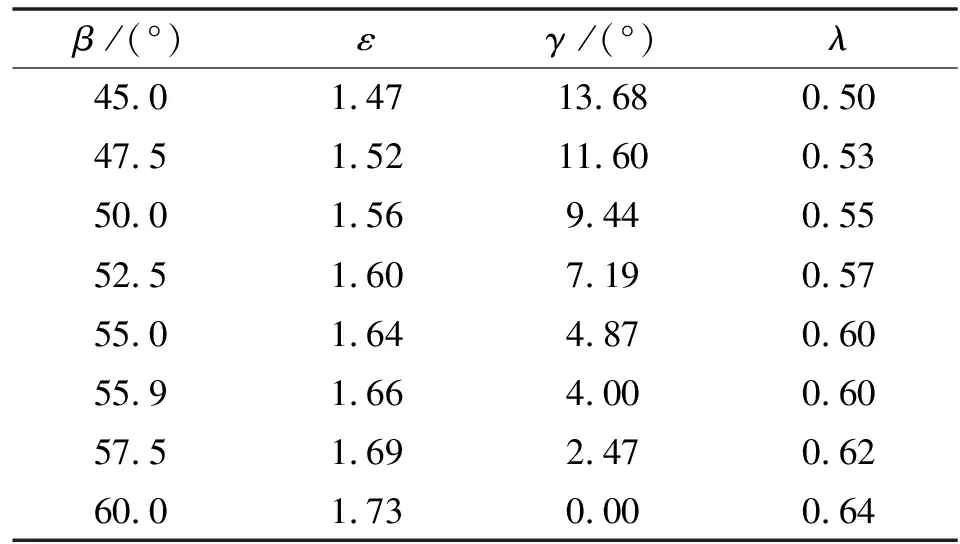
表1 高形转子形状系数和顶封角及容积利用系数
以三叶=55.9°的定点共轭高形转子为例,其模型如图6所示。此时形状系数=1.660 6、容积利用系数=0.604 5,相较于定点共轭普通转子的形状系数=1.517 6、容积利用系数=0.526 7,高形转子的形状系数再提高9.42%,容积利用系数再提高14.77%。相较于具有上限形状系数的三叶渐开线普通转子的形状系数=1.463 8、容积利用系数=0.499 8,形状系数总提高13.44%,容积利用系数总提高20.95%。
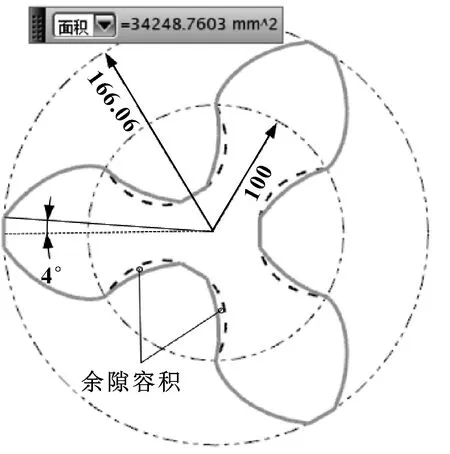
图6 三叶定点共轭高形转子模型
由图6测量出:
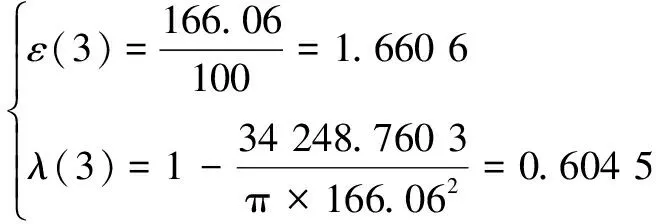
(13)
结果与表1完全一致,说明式(9)—式(12)正确。
采用前述双对称构造法,得与点共轭的节圆外轮廓段的坐标方程(0≤≤),形式上与式(4)完全相同。其中,节圆外轮廓段内0≤≤部分为对应于节点的共轭段,≤≤部分为对应于节点的避让段,如图5所示。
采用前述双对称构造法,得与点避让共轭的内轮廓段在-≤≤内的坐标方程为
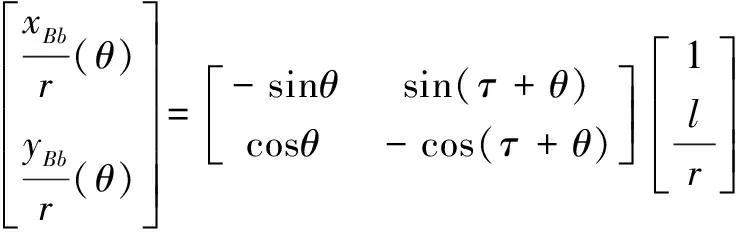
(14)
其中:
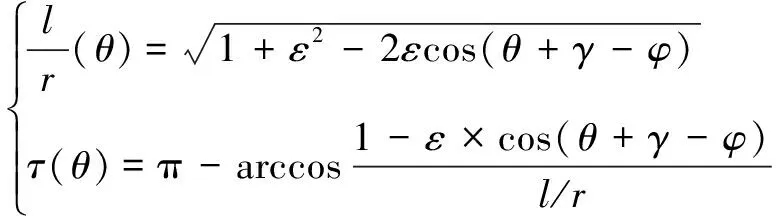
(15)
式中:(,)为图5中段上对应于的点坐标;()为线段的长度;()为线段与线段间夹角。
4 定点共轭高形转子旋转区间内多密封点位
高形转子副在共轭旋转的不同角度区间内,将会出现如图7所示的不同密封点位。其中,为以主转子谷对称轴与从转子峰对称轴重合时为起始位置的旋转角,则0≤<、=、≤<-、=-、-≤<内将分别有5、4、3、2、1个的密封点位。
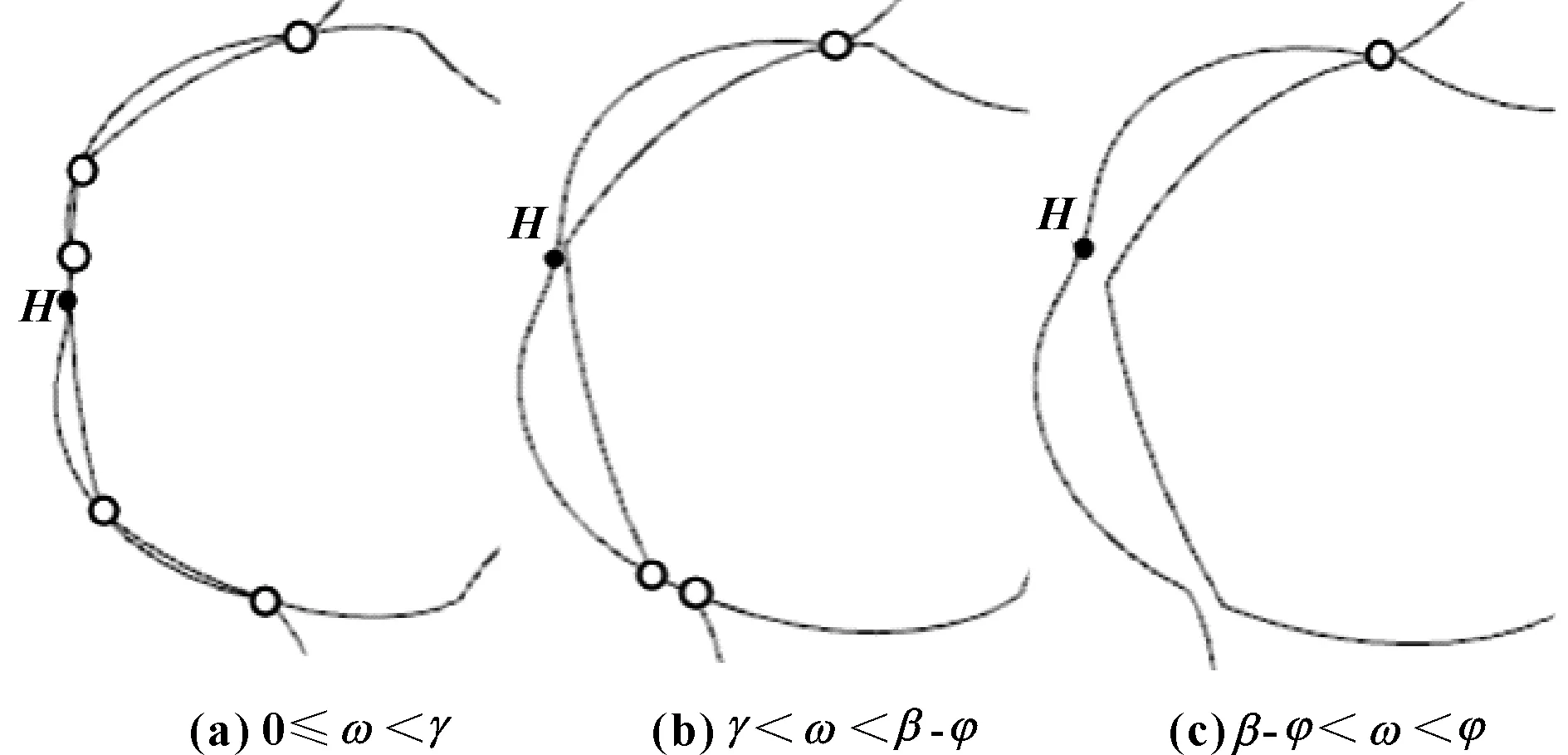
图7 转子副不同区间内的密封点位数
以三叶=55.9°为例,相对于0<<内仅有1个密封点位的普通转子,多密封点位区间占比-1=86.3%,共轭泄漏更小,加上叶顶2=8°的径向等缝隙密封,径向泄漏会更小。
对于像罗茨泵/风机用的凸转子多采用非高速气体介质,因转子间存在较大的非接触间隙,多密封点位不会形成类似齿轮泵的困油现象,或者这种现象很轻微。但是,对于液体介质会形成类似齿轮泵的困油现象,可采用如图8所示的替代圆弧来消除多密封点位。此时,半叶轮廓更简单,加工更容易。
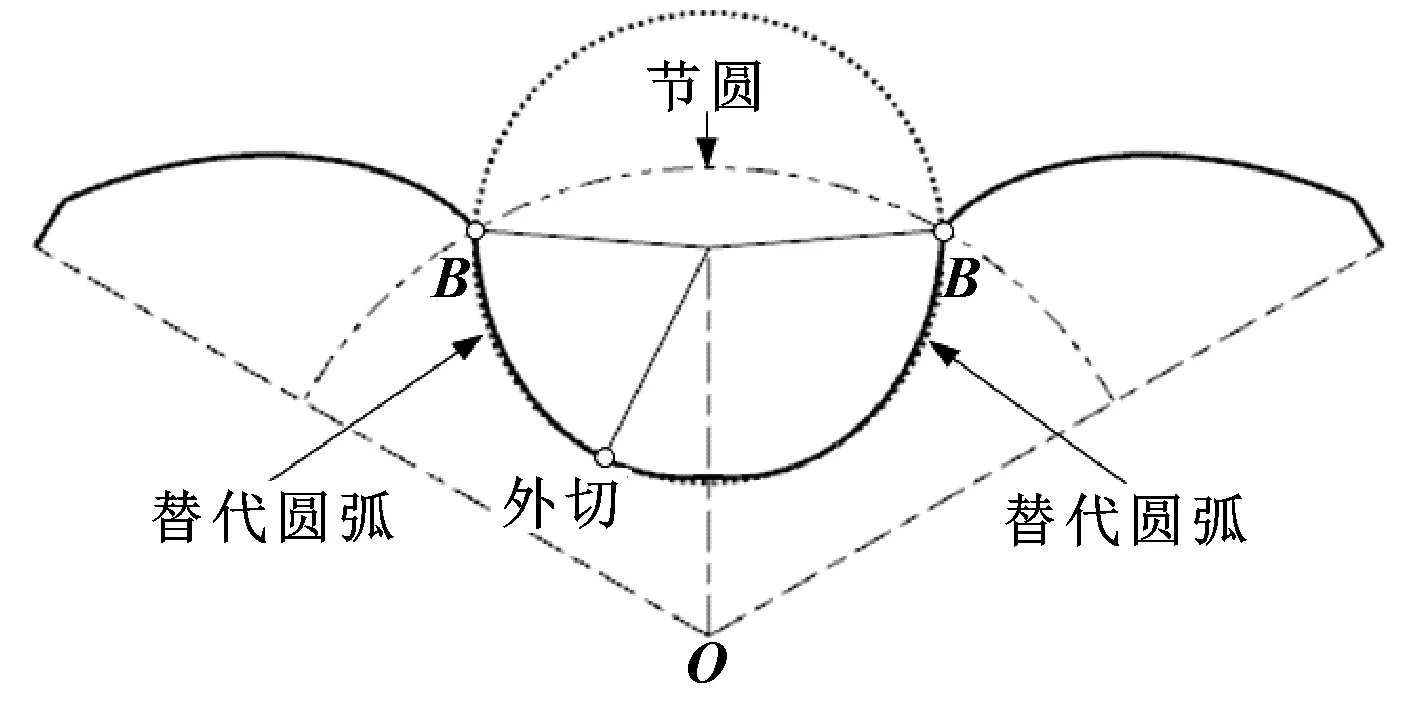
图8 节圆内替代圆弧
5 结论
(1)内共轭段汇聚为轮廓节点时的定点共轭普通转子,具有各种共轭轮廓曲线下极限的形状系数和容积利用系数,如三叶时2个参数分别为1.52和0.53。
(2)定点共轭的高形化构造可进一步取得更大的形状系数和容积利用系数,例如4°顶封角时2个参数分别为1.66和0.6。
(3)高形化构造将形成2~5个密封点位及86.3%的区间占比,能有效减少气体介质的共轭泄漏。
(4)节圆内替代圆弧能有效消除液体介质的困油现象,且轮廓更简单,加工更容易。
