空气涡轮起动机整机结构动力学分步建模与确认策略

张钟鸣 乔思佳 朱钰珏 刘学森 任悦 臧朝平

（1 中国航空工业集团公司金城南京机电液压工程研究中心，南京 211106；2 空军装备部驻南京地区第三军事代表室，南京 210008；3 中国人民解放军海军指挥学院，南京 210016；4 南京航空航天大学能源与动力学院，南京 210016）

0 引言

航空发动机空气涡轮起动机作为航空发动机的辅助起动装置，安装于飞机的飞附机匣。起动机工作时，将空气压力转变为机械能，带动航空发动机运转，实现飞机的正常启动[1]。因此起动机的安全、可靠运行，对飞机的正常启动起着关键的作用。空气涡轮起动机整机系统非常复杂，主要由壳体部件、涡轮、减速器、输出轴等组成（图1）。目前国内对空气涡轮起动机的精确建模研究较少，实现其整机的高精度建模与分析[2-5]，对于起动机的动力学设计和运行工作中的故障分析、诊断，提高产品的可靠性，具有重要的意义。与此相反，航空发动机的整机建模和模型确认已有诸多研究，文献[6-7]建立了含滚动轴承和挤压油膜阻尼器的双转子整机模型。王立[8]等提出了高速转子-支承结构动力学的缩尺相似设计方法。Santiago[9]，陈果[10]，Bonello[11]等人建立了刚性连接的航空发动机整机模型，实现了其动力学分析。马双超[12]使用分步修正策略对航空发动机的机匣进行了动力学模型修正。张根辈[13]，缪辉[14]，秦清珍[15]等提出了螺栓连接、接触界面以及整机模型的模型修正与确认方法。本文提出空气涡轮起动机的整机结构动力学分步建模与确认策略。根据起动机的结构特点，把整机模型分为转子和静子两个子系统，再将子系统分为若干底层结构。通过建立底层结构有限元模型和利用模态试验数据修正模型，再通过薄层单元和摩擦接触模拟连接界面，建立子系统有限元模型和修正，最终建立空气涡轮起动机的高精度有限元模型。

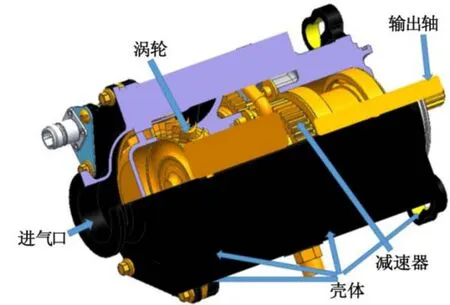
图1 空气涡轮起动机示意图Fig.1 Air turbine starter schematic

1 整机结构动力学分步建模与确认策略

1.1 整机分步建模与模型确认流程

空气涡轮起动机是由轴承将转子系统以及静子系统连接成的复杂整机系统。转子系统包括涡轮转子、主动齿轮、双联齿轮和环形齿轮；涡轮转子与主动齿轮固定连接，构成一级传动结构，将转速传递给双联齿轮，双联齿轮通过齿轮轴固定在壳体上，并与主动齿轮和环形齿轮啮合来起到减速增扭的作用，最终通过环形齿轮将扭矩输出。静子系统由壳体系统和轴承座、密封座衬盖组成，其中壳体系统包括进气壳体、导向器壳体、涡轮壳体和安装壳体。针对其复杂的整机结构，本文提出一种动力学的分步建模与确认策略，以实现整机高精度有限元模型的快速有效建模，流程如图2所示。

图2 整机分步建模与模型确认流程框图Fig.2 Whole machine step-by-step modeling process

整机建模与模型确认共分为以下三步：第一步，底层各结构的建模与模型确认。通过适当简化底层各结构的几何模型，建立其有限元模型，并开展自由-自由状态的结构模态试验。通过模型预测结果与模态试验的数据的相关分析，试验数据对预测模型的修正，得到底层各结构确认的有限元模型。第二步，子系统的建模与模型确认。通过确认的底层结构的连接界面建模，得到子系统的有限元模型，同时对底层结构装配后的子系统进行模态测试，并进行子系统层连接模型的参数修正，得到确认的子系统模型。第三步：整机模型的建立及预测分析。将各子系统结合，得到高精度的整机动力学有限元模型，并进行整机临界转速仿真预测，与试验数据对比验证，从而验证模型的精确性。

1.2 底层结构和子系统的建模理论

1.2.1 底层结构动力学建模方法

底层结构有限元模型精度和规模直接决定了子系统以及整机的模型精度和规模。为了保证底层结构模型精度的同时，也要有较高的计算效率，按照以下建模准则执行。

1）几何结构简化：在实际底层结构中存在各种局部细小的几何特征，例如倒角、圆角以及小孔等。在有限元分网时细小特征会使模型局部自由度快速增加，严重影响计算效率。因此需要删除这些局部细小特征能够使得几何结构更加平整，减少畸形网格的产生，减小模型规模。

2）确定单元类型及划分网格：对于局部几何特征较小而对模型的动力学特性影响较大的结构，可设置较小的网格尺寸来保证局部的网格质量。对某些复杂结构，可以分区域划分不同的尺寸的网格，来保证整体的网格数量以及网格精度。本文模型选用四面体单元分网。

1.2.2 子系统建模方法

在空气涡轮起动机中存在螺栓连接和齿轮摩擦接触两种连接方式。静子系统以螺栓连接为主要形式，通过预紧力计算出薄层单元刚度，建立连接关系。转子系统以摩擦接触为主要形式，建立面与面接触，通过接触单元模拟目标面和接触面。

1.2.2.1 子系统螺栓连接的建模

起动机壳体系统的各部件之间通过螺栓连接，本文采用线性本构的薄层单元来对螺栓连接的接触关系做近似等效，通过改变薄层单元厚度和材料参数来模拟连接刚度，能够较为准确地反映接触面的力学关系。

假设薄层单元的几何尺寸为l1×l2×d，可根据虚功原理得出经等参变换后薄层单元刚度矩阵为

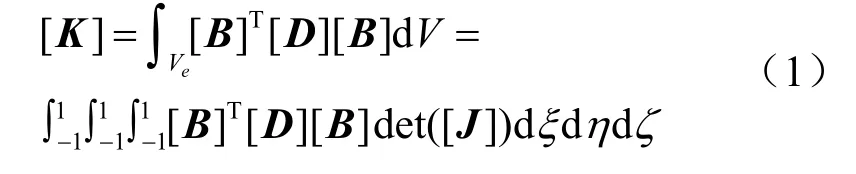
其中为[B]材料的弹性矩阵，[D]为单元几何矩阵，[J]为雅可比矩阵。雅可比矩阵表示局部坐标与全局坐标的关系，其形式为

一般采用数值积分方法对式(6)求解，可采用二节点高斯方法提高插值精度，得到刚度矩阵表达式为

wξwηwξ是高斯积分权函数。在采用有限元方法的动力学分析中薄层单元的本构方程为

式中λ为拉梅常数；G=E/2 (1 +ν)是材料的剪切模量。由于各向同性材料仅有杨氏模量E和剪切模量G两个相互独立的材料参数，可简化为

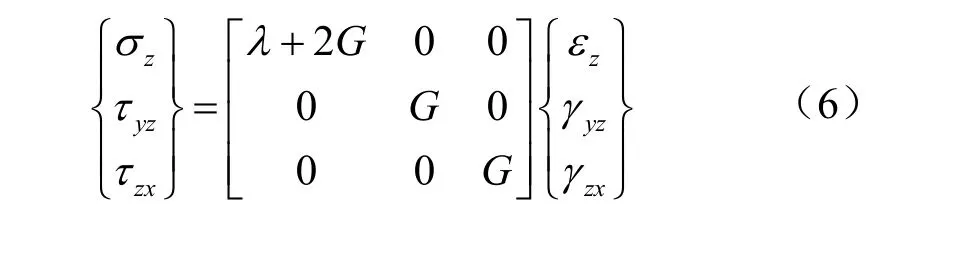
此时法向弹性常数与切向弹性常数是非独立的，二者共同决定接触面的连接刚度。

1.2.2.2 子系统连接摩擦界面的建模

起动机的转子系统存在两组摩擦接触：主动齿轮和双联齿轮的摩擦接触以及双联齿轮和环形齿轮的摩擦接触。在建立轮齿面的接触模型时，需先确定摩擦系数，其大小与轮齿的几何形貌、齿面间的相对滑移以及接触应力等因素有关。目前有多种针对齿面摩擦系数的计算模型，如库伦模型，基于弹流润滑理论的计算模型等。库伦摩擦模型的基础假设为：在啮合过程中摩擦系数的大小维持不变，仅在节点处发生方向的改变。

式中，Ff为摩擦力，µ为摩擦系数，vrel为滑移相对速度，sgn为符号函数。vrel=0时，为粘滞状态，此时Ff=µsN，µs为静摩擦系数。

1.3 模态测试基本理论

被测结构的多自由系统强迫振动运动方程为

其中，M、C、K分别为结构的质量、阻尼、刚度矩阵；{x(t)}为各个测点的响应；{f(t)}为激振力向量。设激振力是频率为ω的简谐力，运动方程可以被表示为

进一步可以求解出结构响应

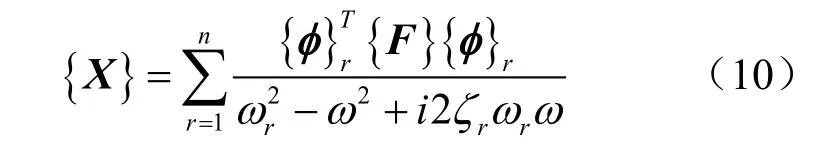
其中{φ}r，ωr，ζr分别为结构第r阶模态的模态振型、模态频率、阻尼比。结构所有自由度的响应{X}，即结构工作变形，是各阶模态响应的叠加。当外力的激励频率等于某阶模态的固有频率时，结构的振动形态为这一阶的固有振型。采用激光扫描多普勒测试，可以快捷得到其固有振型。

1.4 模型确认基础理论

起动机的分步建模过程中，采用相同的技术路线对底层结构和子系统模型进行型确认。模型确认包括对实际结构的模态测试、模态校准、相关性分析以及模态参数的修正等环节，模型确认流程如图所示。

图3 模型确认流程图Fig.3 Model validation flow chart

相关性分析是把简化模型的仿真计算结果与试验数据进行对比分析的过程。通过分析，可得到有限元模型与实际结构的相关度和差异性。在描述模态特性的过程中，相较于模态频率，模态振型更能体现特征。相关性分析中，通过模态置信准则（MAC）评价振型之间的相似度，定义为

其中，φa,φe分别对应简化模型振型以及参考数据振型。MAC主要是利用模态振型之间的正交性原则，通过计算两个振型向量的夹角余弦来评价振型相似性。MAC值介于0到1之间，值为0时，二者振型向量正交，完全不相关；值为1时，两者振型向量完全一致或者成比例。实际工程应用中，MAC值大于0.6时，即可认为两者为同一阶模态，称之为一阶模态对；当MAC小于0.2时，即可视为该两阶模态无关。模型修正是指利用参考数据作为对比，对有限元模型中一个或多个参数进行修改，从而使有限元模型动力学特性和参考数据保持高度一致，更加准确地反映实际结构的动态特性。这里介绍基于灵敏度分析的模型修正方法。

设修正参数为θ，第j阶特征值λj和特征向量φj的灵敏度分别为

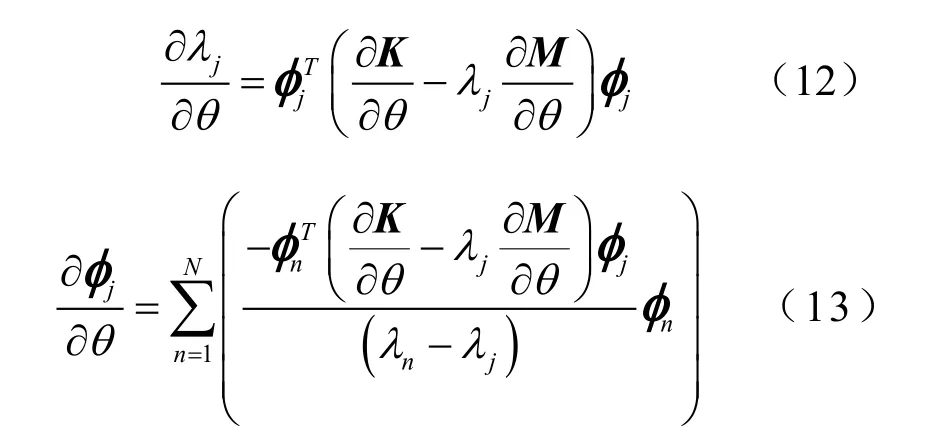
M、K分别为质量矩阵和刚度矩阵，且为对称矩阵。n是模态阶数。通过式(12)和式(13)可以得到各阶特征值以及特征向量对修正参数的灵敏度。对于模型迭代修正中下一步迭代的修正参数的摄动量，也就是修正参数估计值，可以通过最小化某一目标函数得到，推导过程如下：目标函数可以通过模态数据关于修正参数θ的泰勒展zδ开

其中，δθ代表修正参数估计值，为模态试验的响应残差，Si为灵敏度矩阵。将式(14)两边同时乘以，并整理可得下次迭代的修正参数θi+1

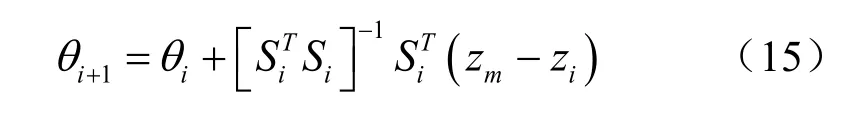
2 空气涡轮起动机整机分步建模应用

2.1 底层结构的建模及模型确认

空气涡轮起动机的底层结构包括转子系统底层部件（涡轮、主动齿轮、双联齿轮和环形齿轮）与静子系统底层部件（进气壳体、导向器、涡轮壳体、安装壳体、轴承座和密封座衬盖）。底层结构的有限元模型，通过对几何模型去除圆角、螺栓孔等对结构动力学特性不敏感的微小特征的简化和网格划分得到。模型确认是通过有限元模型的仿真计算和模态试验的模态参数进行相关分析和基于测试数据的模型修正得到。以涡轮壳体为例，其几何模型删除了部分圆角面以及法兰边螺栓孔，以网格尺寸为8mm建立简化后涡轮壳体的有限元模型，如图4所示，共有37342节点，20800单元，112026自由度。为验证简化模型的精确性，开展基于非接触式测量的模态试验，将试验得到的模态频率与简化模型仿真计算得到的模态频率进行对比。模态试验采用单输入多输出（SIMO）的模态试验方法-锤击法开展模态试验，涡轮壳体测试频率范围为0 Hz ～5000Hz。利用有限元模型进行模态计算，表1中给出了前五阶模态振型与频率。试验布置如图5所示，采取弹性绳支撑的方式来模拟自由边界，力锤从径向敲击，使用激光垂直对准测点位置，进行响应测量。测点布置于涡轮壳体与导向器壳体连接的接触面，以及内部表面上，共布置两圈测点。

表1 简化模型前五阶模态振型Table 1 The first five mode shapes of simplified FEM

图4 简化后涡轮壳体有限元模型Fig.4 FEM of turbine housing

图5 模态试验Fig.5 Modal test

涡轮壳体模态试验得到的频响函数如图所示，对测得的频响函数用导纳圆拟合的方法，分析出5000Hz以内共有5阶模态。

图6 涡轮壳体模态试验频响函数Fig.6 Frequency response function of turbine housing modal test

将模态试验和有限元模型仿真计算得到的前五阶模态频率进行对比，如表1所示。从表中可以看出，第五阶模态频差过大，为-7.46%，需要进行模型修正。将模态试验的数据作为优化目标，对涡轮壳体的弹性模量进行修正，表3给出了修正前后的弹性模量。将修正后的简化模型再与模态试验数据进行对比，并使用相关性分析进行模型确认。修正后得到频差如表4所示，最大频差为2.90%，且MAC值如图7所示，均大于0.78。可认为简化模型能够较为真实地反映出涡轮壳体的动力学特性。

图7 修正后的涡轮壳体有限元模型与试验数据相关性分析Fig.7 Correlation analysis of the corrected finite element model of turbine housing and test data

表2 涡轮壳体简化模型与试验模态对比Table 2 Comparison of simplified FEM mode shape and test mode shape of turbine housing

表3 涡轮壳体修正前后的弹性模量Table 3 Elastic modulus of turbine housing before and after correction

表4 修正后涡轮壳体简化模型与试验模态对比Table 4 Comparison of corrected simplified FEM mode shape and test mode shape of turbine housing

对于其他零部件采用相同的方式建立简化模型，并开展模态试验对模型进行修正和确认，在设计的频率范围内，修正后最大频差以及最大频差出现的阶次如表5所示。最大频差为-4.17%，简化模型的准确度很高，可以进行下一步的子系统建模。

表5 修正后的各部件简化模型与试验数据对比Table 5 Comparison of corrected simplified FEM and test data

2.2 子系统建模及模型确认

在得到起动机各底层部件的有限元模型后，分别对静子系统和转子系统的接触界面进行建模，从而形成子系统的装配模型。

2.2.1 静子系统连接界面建模及确认

静子系统包括壳体系统和密封座衬盖、轴承座。其中壳体系统间存在两组螺栓连接，分别为涡轮壳体-安装壳体的螺栓连接和进气壳体-导向器壳体-涡轮壳体的螺栓连接。通过在接触面间建立实体薄层单元的方式来模拟螺栓连接。薄层单元采用线性本构关系，能够将接触面的复杂接触关系近似等效为线性关系。以涡轮壳体与安装壳体之间的薄层单元建模为例，在涡轮壳体与安装壳体之间建立厚度1mm的实体薄层单元。涡轮壳体-安装壳体的实体薄层连接有限元模型如图所示。实体薄层连接简化模型采用绑定接触，即令实体薄层单元分别与两侧壳体进行刚性连接。

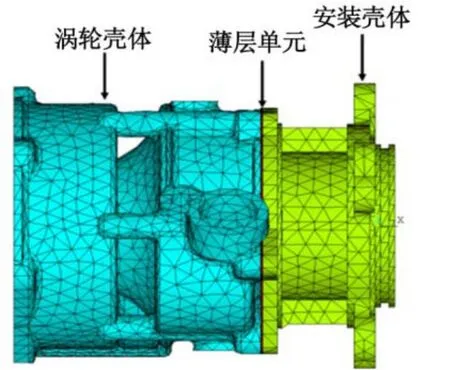
图8 含薄层单元的涡轮壳体-安装壳体连接件有限元模型Fig.8 FEM of turbine housing-mounting housing connector with thin layer element

薄层单元的弹性模量通过实际螺栓连接预紧力下的连接刚度计算得到，为4.71GPa。但以此刚度计算得到的仿真计算结果与试验数据相差较大，这是由于模型简化后，壳体法兰接触面上的节点数量减少，导致连接刚度偏小，因此需对简化模型连接参数进行修正，修正后得到薄层的弹性模量为8.71GPa。修正后涡轮壳体-安装壳体连接件的有限元计算与模态试验数据对比如表6所示，最大频差为-6%，连接件的建模满足要求。

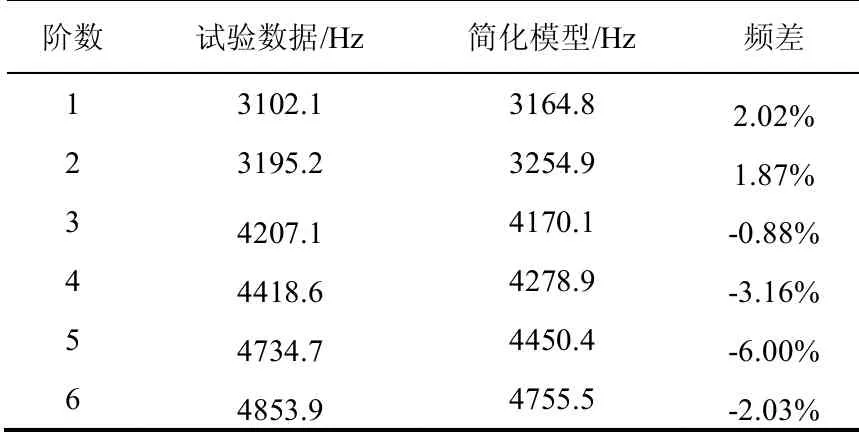
表6 涡轮壳体-安装壳体连接件模型与试验模态对比Table 6 Comparison of simplified FEM mode shape and test mode shape of turbine housing-mounting housing connector

采用同样的方式构建进气壳体-导向器壳体-涡轮壳体连接件的两组薄层单元模型，连接件与底层部件相同，均采用模态试验数据进行修正和确认。确认后两组薄层单元的弹性模量分别为5.17GPa和5.87GPa。在建立三组薄层单元后，得到壳体系统的有限元模型。为了得到与实际的起动机更接近的整机模型，在壳体系统中采用刚性连接建立接触，添加轴承座和密封座衬盖的模型，得到静子系统的模型如图9所示。

图9 静子系统有限元模型Fig.9 FEM of stator system

2.2.2 转子系统连接界面建模

转子系统包括涡轮转子、主动齿轮、双联齿轮以及环形齿轮这四个底层部件。如图10所示，转子系统间存在三组接触对。

图10 转子系统的三组接触Fig.10 Three sets of rotor system contacts

主动齿轮内侧凸台与涡轮卡槽进行定位固定，第一组接触对为绑定接触；主动齿轮与双联齿轮、双联齿轮与环形齿轮之间的接触均为轮齿的啮合，第二、三组接触对为摩擦接触。图11为最终建立的转子系统简化模型。

图11 转子系统简化模型Fig.11 Simplified finite element model of rotor system

2.3 整机模型及其特性分析

在转子系统和静子系统之间共有三组轴承，每组有两个相同型号轴承。第一组在涡轮轴处，第二组在双联齿轮内表面处，第三组在环形齿轮外表面处。均采用combin14单元模拟轴承，三组轴承的支承刚度在表7中给出。最终建立空气涡轮起动机整机简化模型。根据空气涡轮起动机的实际安装形式，在进气壳体和安装壳体处施加全约束。对整机简化模型进行涡轮转子临界转速计算，在坎贝尔图中得到两阶临界转速如图12所示，分别为21067 rpm和56371 rpm。

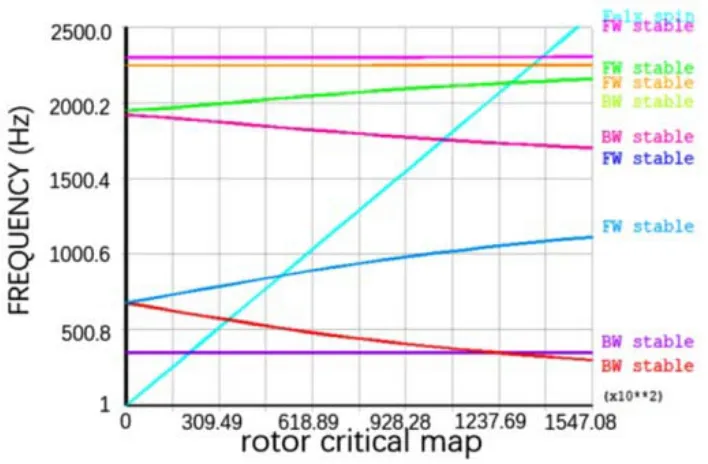
图12 整机系统坎贝尔图Fig.12 Campbell diagram of ATS

表7 轴承支承刚度Table 7 Bearing stiffness

在起动机实际运行试验中，采用加速度传感器进行振动响应测量。由于试验传感器布置在涡轮壳体上，一阶临界转速附近采集到的振动响应幅值较小，难以辨识。在二阶临界转速附近振动响应较大，分析多台起动机的测试数据得知，此时转速在55800rpm到59100rpm之间，与仿真预测结果的相对误差小于4.6%。由此验证了采用分步建模与确认策略建立的整机有限元模型具有较高的准确性。

3 结论

提出了空气涡轮起动机整机结构分步建模与确认的策略，并依据这一策略建立底层结构到子系统再到整机的确认模型，具体结论如下：1）建立底层结构的有限元模型，并基于试验数据对有限元模型进行修正，与试验相比最大频差均小于2.99%；2）通过确认的底层结构的连接建模，得到子系统层的有限元模型。其中，静子系统连接件：基于薄层连接建立连接件模型并对薄层单元进行修正，与试验相比最大频差均小于1.42%；转子系统连接件：通过绑定接触和摩擦接触建立连接关系；3）静子系统与转子系统进行连接，最终得到高置信度的起动机整机有限元模型，进行转子动力学计算的结果与起动机实际测试数据差值在4.6%内，可以验证采用分步建模与确认策略建立的整机有限元模型具有较高的准确性，具有工程价值。