基于单相机的飞行器结构表面应变片三维定位方法

李立欣 周书涛 周江帆 董学金 苏志龙 张东升

（1 上海大学力学与工程科学学院上海市应用数学与力学研究所，上海 200444；2 北京强度环境研究所，北京 100076；3 上海卫星装备研究所，上海 200240）

0 引言

光学三维重建是研究物体三维信息获取的热点方向之一，发展了诸如明暗恢复法、多视角立体视觉、近景工业测量、光度立体法等。其中，多视角立体视觉技术利用视觉几何，从一组普通光学图像中对物体的三维形状和空间位置进行测量和重构，可以大大提高三维测量的效率，有效地构建目标的三维数据，在工业自动化检测和航空航天逆向工程等方面具有广阔的前景。将多视角立体重构与不同领域的应用需求相结合，研究人员们建立了多种具有实用价值的光学三维重建方法。例如，结构光三维形貌测量是建立在双视角成像基础上的一种经典三维形貌测量技术，由于它测量精度高且适用性强，已经广泛应用于许多工业生产领域[1,2]，但结构光需要额外的投影设备配合才能进行测量。RGB-D相机和光场相机的出现为三维重建提供了简单易行的途径[3]，由于这类测量主要采用共轴形式，测量精度有待进一步提高。随着深度学习技术在计算机视觉领域中的快速发展，出现了基于单帧图像的三维形貌重建技术[4,5]，该技术在人脸三维重建得到了应用；然而这类方法目前还只能应用在特定的对象，并且需要大量的前期训练才能提高测量精度。除此之外，采用单相机对物体进行多角度成像是多视角立体测量中一种经济的三维重建技术[6,7]，可从不同角度获得的场景图像中实现对相机姿态和物体三维信息的同时估计，在实际应用中备受青睐，也是本文进行航天飞行器结构三维点稀疏重建的关键方法。在航空航天领域，对飞行器结构进行逆向工程是结构和力学设计优化的关键方法，对结构安全性和可靠性具有重要意义。因此急需发展一种方便、可靠的几何测量方法对飞行器结构进行精确的三维测量。在结构试验中，一般会在结构上布置大量的电阻应变片监测部件主要部位的变形。为了精确对比试验测试与数值仿真结果，需要精确测量所有应变片的空间位置。当飞行器结构尺寸较大和粘贴的应变片的数量较多时，采用传统的逐点式测量方法获取应变片的三维坐标的难度和成本往往会很大。为此通过单相机多视角成像，发展了基于多视觉几何的应变片三维坐标测量与定位方法，以期为航空航天领域飞行器结构的优化设计提供一种方便可靠的三维坐标重构技术。为了实现飞行器结构上应变片三维坐标的精确测量，使用一个标定[8,9]的单反相机对目标进行多角度成像，通过识别布置在结构上的编码点，可靠地估计相机相对于参考帧的姿态信息；然后使用深度学习中的目标检测技术，对图像中的应变片进行识别和坐标提取，并结合特征匹配和相邻帧之间的极线约束对相邻图像中的应变片进行匹配；最后利用三角测量原理，实现应变片的空间定位。

1 测量原理

本文实现大幅面测量区域内应变片的三维定位遵循单相机多视觉立体三维重构的一般步骤，主要涉及相机姿态估计、目标点（应变片）识别与匹配、以及三维坐标重构[10,11]。

在测量操作上，采用定焦相机（记为C）按照如图1所示的方式对目标结构进行多视角成像，其中1C，2C，…，Ci，…,Cn为不同视角下的相机位置。为了能够进行相机姿态估计和应变片坐标重构，在成像过程中需要控制相机使相邻帧Ci和 1Ci+的视场需具有足够的重合区。在获得至少两帧图像后，即可相对于参考坐标系进行相机姿态估计和应变片三维坐标重构，最后根据在视场中放置的比例尺，可以确定结构的物理尺寸。以下对该过程中的主要方法进行详细介绍。

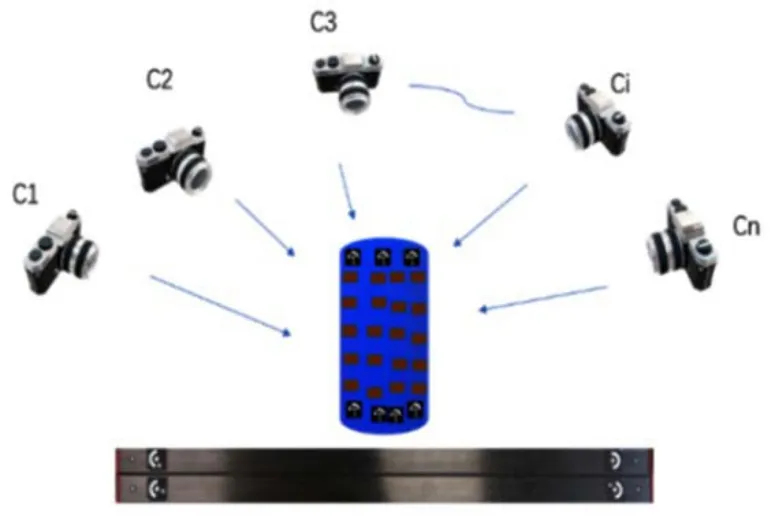
图1 单相机多视觉测量示意图Fig.1 Schematic diagram of multiple view measurement with a single camera

1.1 基于PnP算法的相机全局姿态估计

在应变片三维定位问题中，由于应变片的尺寸通常（最小3mm左右）远小于目标结构的尺寸，且定位精度要求高，因此需要对相机姿态进行可靠估计。为此，本文假设测量相机的焦距固定，在测量前使用张氏标定法对相机内参进行预标定[12]，然后在测量中以布置在目标结构上的编码点为控制点，确定相机的姿态。由于编码点具有唯一性、识别鲁棒性好且定位精度高，可以比自然场景特征提供更加可靠的控制点信息，因此可以得到更精确的相机姿态估计。图2为本文中使用的15位环形编码点[13,14]。

图2 编码点示例Fig.2 Examples of coding points

在检测到相邻图像中的共同编码点后，可采用多点透视算法（Perspective-n-Point，PnP）相对参考坐标系确定相机姿态，包括旋转矩阵与平移向量t∈3。假设以第一帧相机（C1）坐标系为参考系，则相机姿态的确定方法如下。在给定n对三维点和二维图像点对应关系的前提下，可以利用PnP算法确定当前帧相对于参考坐标系的旋转矩阵R与平移向量t。为此，重构第一二帧中观察到的编码点的初始三维坐标是进行PnP姿态估计的关键。由于相机内参已知，可以通过估计前两帧之间的本质矩阵得到第二帧相对于参考系的姿态，然后进行三维重构得到初始三维坐标。假设在第一二帧中得到的编码点坐标对为，其中pj1和pj2采用齐次坐标形式，下标j表示编码点的序号。根据标定相机的极线约束原理[15]，可以得到

其中，K为已标定的相机内参矩阵；E为本质矩阵，表示当前帧相对于参考坐标系的姿态变换关系，即表示平移向量对应的反对称矩阵）。根据式（1）可知，一对编码点可为求解本质矩阵E提供一个方程。尽管是E是一个3×3的矩阵，但其秩为2（即行列式det(E)=0），因此需要八对编码点即可确定本质矩阵E。对本质矩阵进行奇异值分解后，可以得到第二帧相对于参考坐标系的旋转矩阵R和平移向量t。然后，可使用三角测量方法对每一对编码点对应的三维坐标定初始的三维坐标，但由于PnP算法依赖于Pj进行进行重构。尽管上述过程可以确后续相机姿态的估计，因此提高Pj的重构精度有利于提高应变片定位精度。为此，本文进一步采用光束平差法(Bundle A djustment，BA)[16]对Pj进行优化。光束法平差的本质是求解关于相机姿态 (R和t)与三维点Pj的最小二乘优化问题，使得总体重投影误差最小[17,18]。需要注意的是，在应变片三维定位中，为了保证透视投影模型下小尺寸应变的可识别性，相邻两帧相机的姿态变化不宜过大，因此而来的一个问题是相机的基线变化比物距小得多。如果在BA优化中直接以Pj的坐标为参数，往往会存在数值稳定性问题。为此这里采用逆深度参数化的方式表示空间点，然后建立BA优化模型。由于参考坐标系为第一帧相机坐标系，因此上述重构的三维点Pj的Z坐标即为其深度，于是其逆深度可以表示为wj=1/Zj。从而，Pj可以被逆深度参数化为P j=pj1/wj。根据初步估计的旋转矩阵R和平移向量t，Pj可被重投影到第二帧图像得到重投影图像点坐标，然后与观察到的对应点做差得到重投影误差。将所有观察到的编码点的重投影误差进行求和，可得到BA优化模型

其中，N为编码点对数，〈〉为归一化算子。通过求解上述模型，即可得到最优逆深度，然后根据逆深度参数化得到高精度的初始三维点Pj。在初始三维坐标确定之后，可使用PnP算法依次确定后续图像帧相对于参考坐标系的相机姿态。由于在测量中应变片图像序列往往比较长，单纯使用PnP算法会存在一定的误差累计。为了消除累计误差，在新的姿态估计完成之后，可以对其及上一帧应用式（2）中的BA优化，可以同时提高每一帧中编码点三维坐标重构精度和相机姿态的估计精度。

1.2 基于YOLO模型的应变片图像识别

布置在结构表面的应变片尺寸小、数量多，而且外观相似度比较高，因此很难采用人工识别或者传统图像处理的方式完成应变片识别。为了解决这个问题，本文采用深度学习的方式从图像序列中识别应变片的坐标。目前，深度学习的目标检测方法大体上分为2类，即两阶段目标检测方法和一阶段目标检测方法。两阶段的目标检测方法常见的有Faster R-CNN[19]，这一类检测方法往往先处理图像生成候选区域，然后再对候选区域进行分类和回归；其优点是检测精度高，缺点是检测速度比较慢。一阶段目标检测的代表性方法有YOLO[20]和SSD[21]等，这类方法不需要生成候选区域，直接通过图像回归出物体的类别和坐标，不生成二阶段目标检测方法所需的候选框，检测速度快。在考虑应变片的特征后，本文使用YOLO（You Only Look Once）进行应变片识别[22,23]。YOLO模型使用一个单独的 CNN 模型，实现端到端的目标位置检测以及分类；与Faster R-CNN相比，YOLO速度快，而且准确率也很高[24,25]。YOLO算法直接把输入的原始图片分割成互不重合的小方块，然后通过卷积运算遍历每一个小方块，产生特征图，再得到与特征图中对应的每个元素，从而达到目标点位置推理的目的。在应变片检测任务中的具体细节如下。

首先建立应变片图像数据集。对粘贴在结构表面的应变片进行多角度拍摄，通过数据增强的手段扩展样本数量，使得样本数量大于等于训练YOLO模型的经验值1500。然后人工标注每张图像中的应变片的位置。标注完成后，按8:2的比例随机将数据集分成训练集和测试集，随后开展模型训练。采用Pytorch框架，构建了YOLO v 5x模型，并对其进行训练。模型输入端主要包含自适应图片缩放、Mosaic数据增强和自适应计算锚定框。其中，Mosaic数据增强通过对图像随机的缩放、裁剪、排布，将同一组的图像拼接起来，拼接后的图像用于后续的模型训练。训练时，图像按照输入大小缩放为1280×1280像素后分组依次输入Backbone主干网络。Backbone网络模型提取的特征图的长度和宽度相对较大，然而最终分类定位的输出维数相对较小，因此需要对特征维数进行压缩。为此在主干网络和检测头Head之间添加一个Neck层。Neck结构可更好地利用主干输出的图像特征，将其进一步融合后传输到检测头进行分类和定位。经过Neck网络层压缩和融合后传递给Head 输出层，最后输出应变片的类别和图像坐标。为评估训练的YOLO模型的性能，可采用mAP (Mean A verage P recision) 作为模型精度的综合评价指标。在训练完成后，评估模型的mAP@0.5的数值，当该指标大于0.95时，认为模型训练达标。对成功训练的YOLO进行部署后，进行应变片检测。

1.3 应变片的立体匹配和重构

通过第1.1和1.2节，我们可以得到相邻帧之间相机姿态信息和每帧图像中的应变片坐标。接下来就可以通过立体匹配的方法对相邻帧可见的应变片进行匹配，然后采用三角测量计算空间位置。相机姿态估计得到的旋转矩阵和平移向量可为应变片的匹配提供极线约束，这样可以减小搜索范围，提高匹配效率和降低误匹配率。应变片匹配中的极线约束如图3所示。由于应变尺寸很小，且彼此之间相似度较高，因此为了在极线约束区域内得到稳定的匹配结果，需要再引入两个约束条件。首先，将YOLO模型检测到的应变片视为特征点，它们在相机进行移动和旋转时，会因视角变化产生尺度和方向上的变为。为了解决这一问题，本文利用尺度不变特征描述(feature descriptor)[26]提取每个应变片的特征向量，然后在相邻两帧图像中按照距离最近原则进行特征向量搜索，得到匹配分数最高的一对描述子，将它们对应的应变片视为最佳匹配。需要注意的是，此时得到的最佳匹配并不唯一，需要进一步筛选。考虑到拍摄图像时相机的移动范围较小，相邻图像中的目标发生的是仿射运动，所以相邻图像中的应变片和编码点的移动趋势具有高度的一致性。因此，可以依据编码点的匹配关系，确定相邻帧间的仿射变换关系，对上述匹配得到的应变片进行进一步筛选，提高应变片的匹配准确度。最后，结合相机之间的空间位姿关系，即可确定检测出的应变片在世界坐标系中的三维坐标。

图3 极线搜索示意图Fig.3 Epipolar constraint relationship

2 实验验证

实验采用佳能EOS 5D Mark IV单反相机，分辨率为4464×2976像素。为了验证本文方法的重构精度和应变片三维定位的可行性，实验部分包括两个方面的内容。首先，采用精度为1µm两根高精度标尺验证定位精度；然后，对一个粘贴有86个应变计和25个编码点的圆柱形结构（直径300 mm）进行测量。

2.1 定位精度验证

精度验证中使用了如图4所示的两根标尺，标尺上两个定位圆之间的长度分别为949.880 m m和949.606 mm。

图4 精度验证用的标尺Fig.4 Scale bars for accuracy validation

测试中，对图4中包含两个标尺的场景进行5次成像，并对标尺长度进行重构。需要注意的是，为了保证精度测量的合理性，在估计相机姿态时仅使用不在标尺上的编码点。在重构标尺时，以较长的标尺作为长度参考，然后重构较短标尺上两个定位圆的坐标。得到定位圆坐标后，将两个定位圆之间的距离作为标尺长度的测量值，然后与标尺的实际长度（即949.606 mm）进行比较，得到重构误差，结果如表1所示。根据验证结果可知，5次测量得到的最大绝对误差值为0.120 mm，平均值为0.098mm（四舍五入后为0.100 mm）。根据图4可以看出，测量的水平视场大小约为1 m，说明对于1 m大小的物体，本方法的定位精度可以达到0.100 mm/m。

表1 精度验证结果Table 1 Accuracy verification results

2.2 圆柱结构应变片测量

在精度验证之后，使用本文方法对布置在直径为300mm圆柱上的应变片（86个）进行定位测量。在采集图像时，相机环绕目标结构移动，并确保相邻图像有重叠部分，共拍摄32张图片，如图5所示。由于目标结构特征尺寸仅有300 mm，为了不使目标结构在图像中的占比过小，本次测量中使用一根较短的标尺（长度为551.423mm）恢复结构的物理尺度。测量中首先使用训练的YOLO模型识别单反相机拍摄的图像中的应变片。由于采用了重叠成像的方式，每帧图像能够清晰的记录部分应变片的信息，将训练后模型应用到这种重叠图像序列，可以保证能够识别到圆柱结构上的所有应变片，识别效果如图6所示。然后，在确定各个相机的位姿关系后，以第一帧图像对应的相机坐标系为参考，根据第1节中的方法对应变片进行匹配和三维重构。需要注意的是，并非所有在第一帧中的应变片都能够在第二帧中找到对应的应变片，由于拍摄视角的遮挡关系，会有一部分应变片在第二帧中无法找到对应的应变片。因此，在完成对第一帧应变片空间定位后，继续对第二帧中未配对的应变片与第三帧中的应变片进行匹配，然后依次再进行重构。需要说明的是，在此种情况下，应变片的空间坐标是基于前一帧的相机坐标系进行确定的，需要根据坐标转换将其映射到全局参考坐标系。通过上述处理过程，最终完成对圆柱壳表面所有应变片的三维定位，如图7所示。为了说明重构的可靠性，根据应变片的三维定位结果对圆柱进行了拟合，得到圆柱直径为300.052mm，其相对与真实直径的误差仅为0.052 mm。由于测量视场约为0.55 m，可换算得到1 m视场下的定位精度约为0.100mm/m，这与 第2.1节中的结果相吻合。

图5 拍摄的序列图像Fig.5 Sequential images

图6 应变片识别示例Fig.6 Examples of strain gauge recognition

图7 应变片三维重构结果Fig.7 Three-dimensional reconstruction of strain gauges

3 结论

本文介绍了一种基于单相机的多视角三维测量方法，实现了圆筒构件上应变片三维坐标的定位。该方法利用编码点对相机姿态进行高精度估计，然后采用YOLO模型对应变片进行识别，得到应变片的图像坐标。最后基于相邻相机的位姿关系，依次完成所有应变片的立体匹配和三维空间定位。实验表明该方法操作简单，可以实现大幅面结构上小应变片的识别定位；对于1 m以内大小的结构，本方法的定位精度可以达到0.100 mm/m。本文方法不仅适用于应变片，在后续的研究中，将尝试通过训练其它被测小目标物体的深度学习模型，从而重构出这些物体的三维坐标，具潜在的实际应用价值。