适度综合，注重“概念”认知的深度考量——关于“周长”概念测评题的设计与说明

浙江省嘉兴市南湖区教育研究培训中心 费岭峰

浙江省嘉兴一中实验经开学校 李亚群

测评题命制是学生学习质量评价的重要内容之一，命制过程需要依据课程目标、学习目标及学生当下的学习状况三个方面的内容。与传统的测评题相比，素养理念下的测评题不仅需要了解学生在知识理解、技能掌握方面的表现状况，还需要对学生的学习素养做出诊断与把握，以便有利于教师在后续的教学中为发展学生的学习素养提供全面的帮助。概念认知作为小学数学教学的重要内容，当然也不例外。以下结合几道关于“周长”概念的理解与应用的测评题，就核心素养理念下的“概念”认知的测评题命制，谈一些想法与实践。

周长是什么？周长属于一维长度的范畴。对周长概念的认知，一般包括认识、理解与应用等几个水平层次。传统的测评题编制过程中，相对单一的指向一个维度的测评更多些，比如指出或测量、或计算某个图形的周长等。这在测评学生对概念的认知过程中也是必要的。但核心素养理念下的测评，需要在了解学生对概念的认识、理解与应用水平的同时，适度考虑测评题对分析、综合、评判甚至创造的要求，在测评学生基础知识理解与基本技能掌握的基础上，关注学生数学基本活动经验与基本数学思想方法的形成、应用水平，从而体现素养立意测评的特征与意义。

典型题例1：下面的图形有周长吗？如果有，请用水彩笔描出它的周长。

[内容]人教版数学三年级上册“长方形和正方形”单元“周长”的相关知识。

[设计意图说明]“长度”是认识图形的重要维度之一，而“周长”又是认识平面图形的重要内容。认识周长、理解周长的含义，是“周长”概念学习的重要目标。传统教学中，对学生是否认识了周长、理解了周长的含义，一般的检测会以单个的图形进行（比如就上题中的某个图形请学生做出描述或判断）。这样的测评题当然能对学生对周长概念的认识水平有一定的了解，但相对单一，对学生综合分析与判断的能力的关注相对弱化。以上测评题则以多个图形整体呈现，请学生做出判断，并要求有“描”这样的操作要求跟进，对学生关于“周长”概念的认知状况的了解则会更加全面。在实际解答时，学生一般会出现以下三种情况：

情况一：能够对图1、图2做出准确判断，对图3、图4的判断则较为困难。

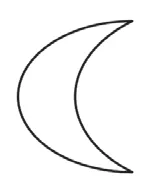
图1

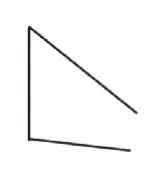
图2

图3

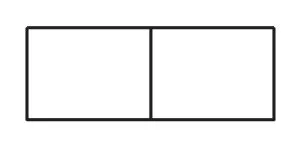
图4

情况二：能够对图1、图2做出准确判断的同时，对图4也能做出准确判断，即能够正确描出图4整个图形的周长（外面一圈）。

情况三：能在对图1、图2和图4做出准确判断的基础上，还能对图3进行准确描述，即能够描出图3中三角形的周长（因其也是一个封闭图形）。

以上三种结果，反映了学生对“周长”概念理解的三种水平。情况一，表明学生对“周长是指封闭图形一周的长度”的基本认识是有的，但深度理解不足，延展力不够，当出现一些干扰因素时，判断图形的周长就会出现困难；情况二，表明学生对图形周长的概念相对比较清晰，不受图形内部信息的干扰；情况三，表明处于此水平的学生深度理解了“周长”的含义，对他们来说，只要发现封闭的平面图形，便能够描述这个图形的周长。对于对周长具有此认知水平的学生，结合图4进行追问，学生还有可能表述出不同图形的周长，即除了可以描述整个图形的周长，还可以描述图中两个小长方形的周长。

此题一般在本节内容学习后用来对学生的学习状况进行检测，当然也可以在单元练习中作为了解学生对周长概念理解状况的测评题。

典型题例2：下面的长方形被分成甲、乙两个部分，哪个部分的周长比较长？请写出你的想法。

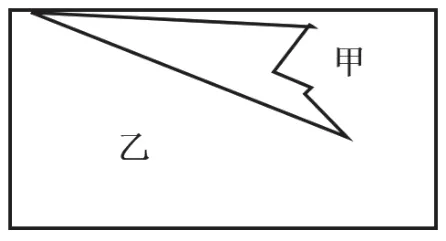
[内容]人教版数学三年级上册“长方形和正方形”单元“周长”的相关知识。

[设计意图说明]同样作为“周长”内容学习后即时跟进的测评题，与上一题相比，本题有更高的分析与综合的要求，不仅考查学生对周长概念的理解，同时也将图形的特征纳入分析中，考查学生综合应用知识分析和解决问题的能力。相对来说，此题对学生的素养要求更高。另外，在平时的考查中，我们一般只需得出结果。但在素养立意的测评中，我们还需要学生表达出相关的思考过程，以便更加准确地把握学生的思维状态，了解学生解答此问题的过程。实际解答时，有学生受了“面”的直观大小的干扰，做出了错误的判断（即或甲周长大于乙周长，或甲周长小于乙周长。上图中回答后者的可能性更大些，因为甲的面积明显小于乙的面积），解答正确的学生会表现出以下两种思路：

思路一：量出长方形的长和宽，再量出中间那条曲线的长度，然后分别将长、宽与曲线的长度加起来后进行比较。

思路二：根据长方形“对边相等”的特征进行推理。即甲图形的周长是“长+宽+曲线的长度”，乙图形的周长也是“长+宽+曲线的长度”，因为甲、乙两个图形的周长均是以“长方形的长、宽的长度和+公共曲线的长度”来计算的，所以两个图形的周长是一样的。

以上两种思路，反映了学生对图形周长的理解是正确的，但在解答问题时，其思维水平还是有差异的。产生思路一的学生，对图形的周长是理解的，即“围成这个封闭图形的所有边的长度之和”，当然，其思维显然处于需要得到具体的“量”才能判断结果的水平；产生思路二的学生，能够结合图形的特征，对问题进行综合分析，在理解周长含义的基础上，借助图形特征进行推理，其对“量”的理解、信息的综合分析水平显然高于思路一的学生。

类似的测评题还有如“下图中大正方形的周长是小正方形周长的几倍”这样的题。同样是在“面”的干扰下，检测学生对周长的本质“图形一周的长度”的理解水平。解此题首先要找到大正方形的周长，再根据大正方形与小正方形边的关系（小正方形边长的2倍是大正方形的边长）来判断大正方形周长与小正方形周长的倍数关系。当然，此题受到“面”的干扰可能更大一些，更适合用于学完“面积”与“周长”知识后，作为概念比较与辨析时的检测题。

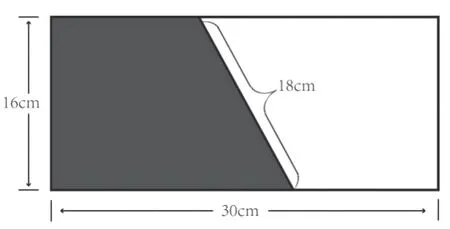
典型题例3：如下图，两个完全一样的直角梯形拼成了一个长方形。其中一个直角梯形的周长是多少？

[内容]人教版数学四年级上册“平行四边形和梯形”内容中图形特征的相关知识。

[设计意图说明]认识平面图形一般有两条路径，即从“边”的角度来认识与从“角”的角度来认识。“周长”即是从“边”的角度，基于长度属性来认识平面图形。学生在三年级学习了“周长”后，在四年级“平面图形的认识”中，再次出现“周长”的相关知识，这也是帮助学生全面建构图形特征必不可少的过程。题干内容表述文字虽然不多，但涉及的知识点却有长方形、梯形、周长的概念等，具有较强的综合性。本测评题作为2022年某市四年级期末检测试卷中的习题，学生在解答时出现的几种典型错误如下：

错误一：直接计算长方形的周长，即（16+30）×2=92（cm）。

错误二：计算了长方形的周长，再除以2，即（16+30）×2=92（cm），92÷2=46（cm）。

错误三：计算了长方形的面积，再除以2，即

16×30=480（cm），480÷2=240（cm）。

三种典型错误，第一种错误是由于学生审题不清，后两种错误则反映了四年级学生在“周长”概念的认识上仍然存在着问题。问题一（即错误二），学生对在复杂情境中对梯形周长的认知不清，将其简单化为整个图形周长的一半，实质也是在“周长”概念表象建立过程中出现了问题；问题二（即错误三），学生混淆了“面积”与“周长”的二维与一维属性，这也是学生在学习了“面积”相关知识后，时常会出现的问题，实属正常情况。同时也表明，在新知学习后将旧知与新知结合起来考查学生对知识的整体把握情况，有着极为重要的现实意义。

在对正确的答案进行分析后，发现学生的解答思路主要表现为两种：

思路一：16+30+18=64（cm）。用此种方法解答的学生，对平面图形周长的认识相当清楚。要求这个直角梯形的周长，就是求直角梯形上底、下底和两条腰的长度和。根据图中的相关信息，两条腰的长度已知（16cm和18cm），上底和下底的长度分别是多少虽然不知道，但它们的长度之和是30cm。于是将这些长度加起来，即为这个直角梯形的周长。

思路二：（16+30）×2＝92（cm），92÷2＝46（cm），46+18＝64（cm）。从思维水平来说，用此种思路解答且正确的学生，其对周长概念的理解还是相当深刻的，而且思维水平也比较高。因为他们不仅知道求直角梯形的周长就是求上、下底和两腰的长度和，同时也知道可以借助整个图形去思考解决这个问题。即在算出长方形周长的一半时，还能够将18cm这条腰的长度加上去。这表明：这部分学生不仅知道梯形的周长是哪一部分，还能够厘清直角梯形与拼成后的长方形之间的关系。显然，他们的高阶思维能力也比较强。

典型题例4：超市牙膏“买一送一”。将下图这样的两盒牙膏用透明胶带绑起来，绑一圈至少需要多少厘米长的透明胶带？（胶带重叠的部分忽略不计）

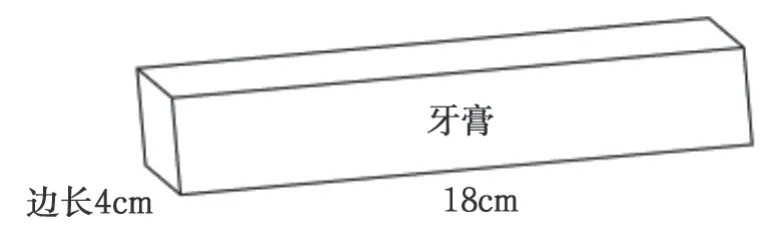
[内容]人教版数学五年级下册“长方体和正方体”与“周长”的相关知识。

[设计意图说明]“周长”作为一种图形认识中的长度属性，同样也是认识立体图形特征时的重要维度之一。这也是图形认识从一维到二维再到三维的一个系统建构的过程。同时也表明，将孤立的数学知识纳入知识系统中进一步理解也是数学学习系统性的基本特点，还是学生综合分析能力发展的重要过程。显然，此题将周长知识结合立体图形的认识进行考查，便具有了更强的综合性。这对学生的空间想象能力与概念应用能力的要求更高。学生在解答此题时出现的两种典型思路事实上也正反映了不同的思考与解决问题的水平。

思路一：算出绑扎一个牙膏盒所需要的胶带长度，然后乘2，再去掉重合的两条边的长度。当然，以这样的思路来解答此问题时需要理解，两盒牙膏重叠起来时，所求胶带长度其实由原来的“8条边长（8个4cm）的和”变成了“6条边长的和”，中间2条边重合后，就不属于周长部分了。因此，用此种思路解答的学生，很容易在这个点上出现错误，可能不会去掉这两条边，还有可能只去掉一条边。

思路二：直接计算一个长8cm、宽4cm的长方形的周长。以此种思路解答这道题的学生，其脑海中已经建构了两个盒子重叠后，算所绑胶带长度的问题其实就是求一个长方形周长的问题。这个过程对学生的空间想象能力要求比较高，同时要求学生对图形的特征及图形拼组后“边”的变化有较为清晰的认知。值得注意的是，本题题干中并没有出现“周长”字眼，学生需由一个长方体想象两个同样的长方体拼组后的立体图形，并通过问题情境的描述，还能从立体图形中抽象出一个平面图形。能够这样思考并解决这个问题的学生，其思维水平已经比较强了，因此解题的正确率也会比较高。

另外，此测评题的综合性还体现在，除了结合生活情境、具有现实意义，从“量感”发展的角度来看，将“周长”概念的理解置于抽象的数学分析中，周长概念的应用经历了一个从“线”到“面”再到“体”的直观演进过程，同时在解决问题的过程中却又经历了一个从“体”回到“面”再到“线”的抽象概括过程。事实上，这也是周长概念系统化建构的必要过程，因为对周长概念的理解当然不能停留于对线的理解水平，它应该被纳入图形认知的系统中，在发展周长“量感”的同时，经历从一般的直观感知理解水平上升到直观想象甚至数理抽象的认识过程，以真正将“周长”上升到长度维度作为认识图形、发展空间观念的重要内容。这也许就是适度综合测评题的意义与价值。