基于不同破坏模式的盾构隧道掌子面支护力上限分析

曾明生，王文法，康海波，王华玲，李智，何毅

(1.四川公路桥梁建设集团有限公司 公路隧道分公司，四川 成都 610200；2.西南交通大学 地球科学与环境工程学院，四川 成都 611756)

随着隧道开挖，围岩发生扰动进而导致应力重分布，掌子面后方岩土体存在变形和破坏的风险。因此，在施工过程中如何维持隧道掌子面的稳定是当前学术界的焦点问题，其关键在于合理确定掌子面支护压力的大小。一方面，支护压力过小则起不到支护作用，导致隧道坍塌破坏；另一方面，支护压力过大会造成掌子面后方的隆起破坏。在早期的研究中，判断掌子面稳定性大多是建立在原位和室内试验上的一些经验公式，如BROMS等[1]提出的不排水条件下黏土隧道掌子面稳定系数法。然而早期的这些经验公式只是定性的分析，无法得到具体的支护压力值，很难应用于实际工程。因此，如何定量分析支护压力对隧道掌子面稳定性的影响是一个重要课题。随着理论研究和计算机的蓬勃发展，求解此问题的方法主要有：极限平衡、数值分析和极限分析三大类。ANAGNOSTOU等[2]构造矩形和楔形块体，得到合理的支护压力以维持排水条件下的隧道稳定；徐前卫等[3]据极限平衡理论的条分法原理，推导出了基于不同地层隧道上覆土的掌子面极限状态方程。极限平衡法因其构造简单、计算简便的优势被广泛应用，不足之处是计算结果与实际工程相比有较大出入。AN等[4]基于温克尔地基模型和刚体极限平衡法并通过FLAC3D数值模拟,对超前小导管下的隧道掌子面围岩稳定性进行了分析。ZAMORA等[5]采用ABAQUS 3D®有限元软件进行数值计算，并评估了对掌子面支撑和稳定压力的需求。有限元极限分析既有严密的理论又兼顾有限元法的适用性，SLOAN等[6]采用极限分析有限元法研究了非均质地基中浅埋环向隧道的稳定性问题。杨峰等[7]改进了刚体平动运动单元上限有限元方法(UBFEM-RTME)，求解了非均质黏土地层稳定性问题。数值分析对于分析破坏机制和极限支护压力有重要的参考价值，但由于其本身的复杂性难以在行业规范中推广。极限分析上限法理论严格，可以较好地界定真实解的范围。一些学者将Hoek-Brown破坏准则[8]和非线性Baker破坏准则[9]与上限法结合起来分析掌子面稳定性。近年来，通过极限分析上限法结合多块体理论[10-12]对隧掌子面支护压力进行研究成为了隧道领域的热点，这也是本文所探讨的。例如，双对数螺旋线[13]，交叉—覆盖层模式[14]等一系列多块体模式，按照极限分析上限法的原则建造模型来求解隧道掌子面的极限支护压力。多块体极限分析上限法具有很强的适用性和极大的参考价值，但也及其依赖于多块体模型的构造，合理的模型决定了求解问题的准确性。本文针对浅埋隧道，将文献中已提出的截锥-对数螺旋-三角形破坏模式中的计算方法做进一步优化。并在此基础上提出一种新的矩形-对数螺旋-三角形的多块体破坏模式，推导了2种模式的掌子面支护压力的表达式，并将其转换为类似太沙基地基承载力分析的三项叠加形式。通过OPTUMG2软件建立极限分析条件下的隧道模型，求解出掌子面的极限支护压力。对2种破坏模式和数值模拟求得的支护压力随隧道埋深比、土体内摩擦角和黏聚力的变化规律进行探讨。

1 隧道掌子面模型

本文依托二维平面隧道，采用极限分析上限法对掌子面进行研究。如图1所示，隧道直径(拱顶与拱底之间的距离)为D，埋深(即地表到掌子面顶部的距离)为C，隧道埋深比为C/D，地表承受均布荷载q，沿隧道掌子面作用均布支护压力σt，模型土体重度为γ，黏聚力为c，内摩擦角为φ。

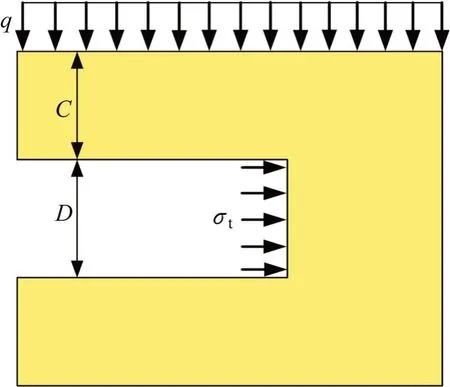
图1 隧道模型示意图Fig.1 Tunnelmodel schematic

需要解决的问题是在土体重度γ，地表荷载q和隧道开挖直径D为固定数值的情况下获得支护压力在不同的埋深比C/D，黏聚力c和内摩擦角φ影响下的极限解和变化规律。固定参数如表1所示。

表1 模型参数Table 1 Modelparameters

2 掌子面破坏模式

2.1 模式1

将吕玺琳等[15]提出的截锥体-对数螺线-三角形破坏机构适当优化。假定掌子面的破坏模式由3部分组成，分别是2个刚性块体a,c和一个剪切块体b。刚性块a为一个底边长为OB，顶角为2φ的等腰三角形O′OB；构造边OE=边AE的等腰三角形OAE(底角等于π/4-φ/2)，命名为块体c，材料属性为刚性；对数螺旋区OBE构成了剪切块体b，对数螺线由起点旋转到终点，即从起点B到终点E。按照图2将CHEN[16]中的公式进行变形得到，

其中，r0可由几何关系推导获得，图中

滑动面相对速度方向与滑面之间的夹角为φ，符合关联流动法则，滑块a，b，c的速度场构建如图2所示。

图2 模式1极限分析Fig.2 Pattern1-lim itanalysis

2.1.1 外功率块体a重力做功功率为

块体b为剪切区，需对整个曲边三角形进行积分。对数螺旋线块微元如图3所示。

图3 微元做功Fig.3 M icroelementwork

此处对文献[2]的微元速度做出优化，取微元3点横坐标的平均值作为速度重心，微元速度为

剪切块微元的重力做功功率为微元面积dA，土体重度γ和微元速度v三者的乘积，即

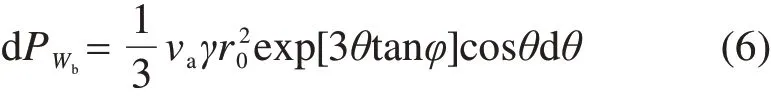
从θ0-θh积分可得

刚性块体c的重力做功功率为

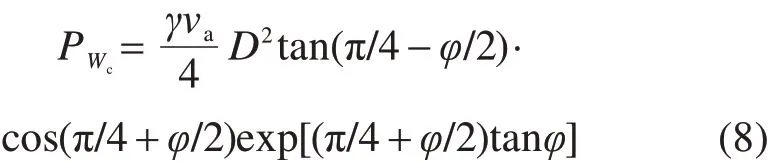
地表荷载做功功率为

支护压力做功功率为

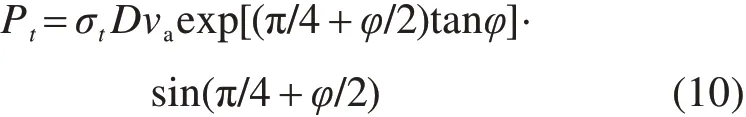
2.1.2 内功率刚性块体a在OO’和O’B间断面上的内能耗散功率为

刚性块体c在间断面AE上的内能耗散功率为

对数螺旋区域的内能耗散由2部分构成，一部分是剪切块体b的内能耗散功率，另一部分是速度间断面BE上的内能耗散功率，且二者相等，可得

2.1.3 极限分析上限求解

按照极限分析上限定理的求解原则，即令外功率等于内能耗散功率，可得

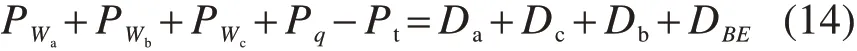
将式(4)，(7)～(13)代入式(14)中，移项后可得支护压力σt的表达式。将支护压力的表达式写成类似地基承载力3项系数之和的形式，即

式中，

2.2 模式2

由于模式1在隧道埋深比较大或者摩擦角偏大的情况下，地面荷载以及上覆土体的自重作用考虑不足。所以模式2在其基础上进行改动，将块体a构造成随隧道埋深变化的矩形，充分体现土体自重以及地表超载的影响。速度场构造如图4所示。

图4 模式2极限分析Fig.4 Mode two lim itanalysis

2.2.1 外功率刚性块体a的重力做功功率为

地表荷载做功功率为

剪切区b和刚性块体c的重力做功功率和支护力做功功率与模式1相同，详见式(7)～(8)和式(10)。

2.2.2 内功率刚性滑块a在速度间断面FO和GB上的内能耗散功率为

剪切区b，速度间断面BE和块体c在间断面AE上的内能耗散与模式一相等，见式(13)和式(12)。

2.2.3 极限分析上限求解

同理根据极限分析上限法，令外功率等于内功率，将式(7)，(10)，(8)，(12)～(13)和(19)～(21)代入式(14)中，可得同式(15)一样的支护压力表达式，其中

3 数值模拟

通过OPTUMG2建立极限分析条件下沿隧道纵向中线剖开的二维平面掌子面模型。模型长为2L1，埋深为C，隧道直径为D，如图5所示。

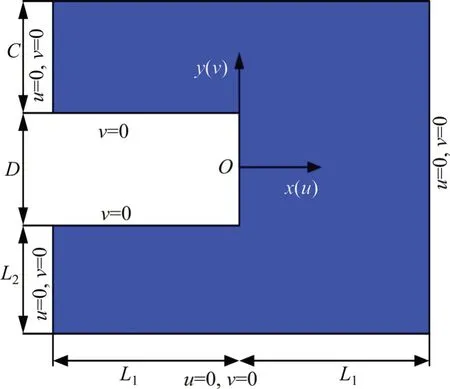
图5 隧道模型Fig.5 Tunnelmodel

模型的边界条件通过法向和切向的速度来解释。模型的左边界、右边界和下边界完全约束，从而达到消除边界效应的目的；在隧道开挖面上、下边界施加法向约束，约束掌子面拱顶和拱底的位移变形，用来模拟开挖之后的隧道衬砌；模型上边界和掌子面上不施加任何约束，来模拟正常情况下的隧道掌子面变形和地表的沉降。

地表施加固定分布荷载来模拟地表荷载，掌子面上施加乘数分布荷载来模拟掌子面支护压力。这里的乘数分布荷载是OPTUMG2中的一种可以随模型稳定系数变化的量，向洞口方向施加来模拟极限状态下的主动土压力(向洞内挤出)破坏，收敛后所得到的乘数荷载数值即为极限支护压力。数值模拟选取Mohr-Coulomb本构模型，隧道模型的几何、土体参数与上述2.1和2.2节相同(详见表1)。

通过OPTUMG2内置上限分析法计算出极限支护压力，并输出内能耗散云图，分别取C/D=0.3和C/D=1.0，如图6所示(取模型土体参数黏聚力c=2 kPa，内摩擦角φ=15°时为例)。

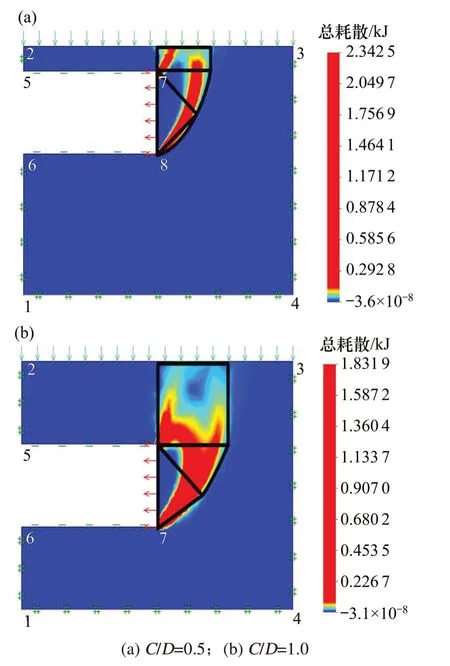
图6 内能耗散Fig.6 Internalenergy dissipation

现将模式2和数值模型计算得到的破坏机构的几何形状进行对比(OPTUMG2模型中的破坏机制已经考虑了剪切耗散的分布)。可以看出，模式2破坏机构的几何轮廓跟OPTUMG2模型给出的掌子面后方的破坏形态基本一致。需要注意的是，多块体模型与数值模型中失稳土体内部的能量耗散面有所区别，这导致二者分析结果并不完全相同。上述分析表明，模式2的破坏机构能够合理地预测掌子面后土体的破坏形态，可以进行下一步极限支护压力的对比分析。

4 结果分析

根据第2节建立的极限分析破坏模式和第3节数值模拟软件OPTUMG2建立的模型对隧道掌子面稳定性进行分析。所得结果能够为理论分析和实际工程提供有价值的参考和新的优化方向。

4.1 支护压力随黏聚力的变化

控制内摩擦角(φ=15°)一定计算得到的极限支护压力解与土体黏聚力c的变化关系如图7所示。从图中可以清晰地看出，模式1，模式2和OPTUMG2的支护压力变化规律相同，都是随黏聚力的增大而减小，且呈线性变化，这说明土体黏聚力越大，隧道掌子面越稳定，需要的支护压力就越小。在同一黏聚力下，对于模式2和OPTUMG2而言，支护压力随埋深增加而增大，如图7(b)和7(c)。

模式1中掌子面上方的块体a(截锥体)的几何形状受到隧道埋深C和内摩擦角φ的控制。在φ=15°的条件下，当埋深比C/D≥1时，块体a就变成了一个面积固定的三角形刚性块体，也就是说模式1的破坏机构将不会再随埋深增加而改变，即极限支护压力是一个定值。所以图7(a)中埋深比C/D≥1的曲线都将和C/D=1的曲线重合。而且随着隧道埋深的增加，块体a变成三角形时，模式1破坏机构将不会再受到地表荷载的影响，3项系数中的Nq等于0，地表荷载的影响被忽略，所以C/D=1时的极限支护压力比C/D=0.5和0.7时的极限支护压力相应地减小。这也是模式1需要继续优化的地方。

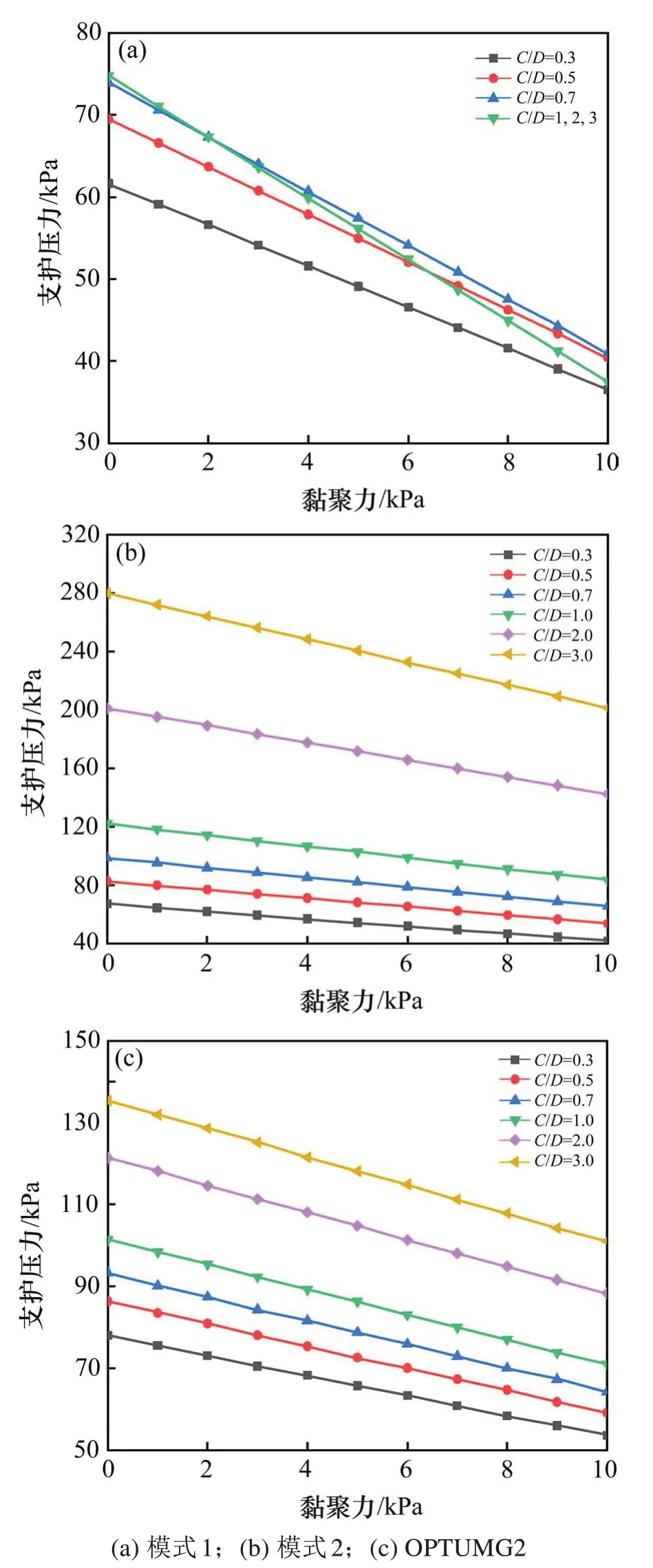
图7 黏聚力的影响(φ=15°)Fig.7 Effectof cohesion(φ=15°)

4.2 支护压力随摩擦角的变化

极限支护压力和内摩擦角φ的关系如图8所示。

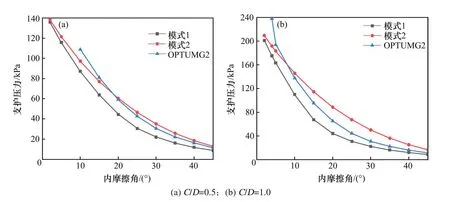
图8 内摩擦角的影响(黏聚力c=2 kPa)Fig.8 Effectof internal friction angle(cohesion c=2 kPa)

按照控制变量法的原则，控制黏聚力(c=2 kPa)一定,埋深比C/D分别为0.5和1的时候，讨论内摩擦角φ的变化对支护压力的影响。从图中可以看出，模式1，模式2和OPTUMG2的支护压力变化规律相同，都是随着内摩擦角的增大而减小，内摩擦角越大，隧道掌子面越稳定。

需要注意的是，OPTUMG2在建模的时候要考虑模型自身的稳定性，不同的埋深所对应的维持模型自身稳定性的最小摩擦角不同，因此C/D=0.5时(图8(a))从φ=10°开始分析，C/D=1时(图8(b))从φ=4°开始分析。

就三者之间的比较而言，模式1的极限支护压力是三者中最小的，这一分析模式可能会低估掌子面的极限支护压力。模式2和OPTUMG2得到的计算结果比较接近，且模式2的极限支护压力略大于数值计算结果，可能会略高于掌子面实际需要的支护压力，在三者中是最安全的。当内摩擦角逐渐增大到φ=45°时，随着土体强度增高，三者的极限支护压力将趋于一较小的稳定值。

4.3 支护压力求解比较

接下来讨论在内摩擦角(φ=30°)一定，通过选取不同的隧道埋深，研究极限支护压力随黏聚力的变化规律。以及在相同参数条件下，三者之间的极限压力值的比较。如图9所示，与(1)结论相同，在同一隧道埋深和内摩擦角下，三者的支护压力的变化规律是随黏聚力的增加而减小且呈线性递减。当内摩擦角大于某一角度时，模式1所求得的支护压力将不再随隧道埋深的改变而变化，所以该模式与实际情况存在一定的偏差，有进一步优化的必要。在隧道埋深比较小的时候，模式2可以较理想地考虑到隧道埋深以及上覆荷载作用的影响，得到的支护压力与数值模拟相近；然而随着隧道埋深的增加，模式2当中的上覆刚性块体自重的作用将会被放大，超过数值模拟中的最大值，仍有改进的必要。

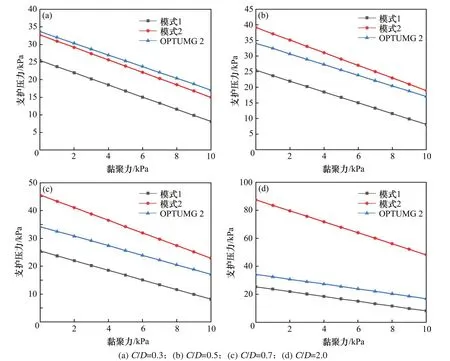
图9 黏聚力的影响(φ=30°)Fig.9 Effectof cohesion(φ=30°)

5 结论

1)合理的破坏机构是多块体极限分析上限法的核心，并且能够和实际破坏情况相互对应，为确定隧道掌子面极限支护压力提供了一种简单易行的方法，对实际工程具有一定的指导意义。

2)隧道掌子面的极限支护压力和土体内摩擦角呈负相关；随土体黏聚力的增加线性减小；在摩擦角较小的时候，支护压力随隧道埋深的增加而增加，当摩擦角增大到一定值时，隧道埋深的改变对支护压力影响甚小。

3)模式1在内摩擦角较大的时候，由于模型上覆破坏块体的特性，地表超载的影响将被忽略，土体自重的作用也相应削弱；模式2可以很好地弥补地表荷载的作用，但在隧道埋深变大时，上覆破坏块体的自重影响较大，可能超过实际作用的上覆土体。因此在地表荷载作用面积和上覆刚性快的模型构造上存在进一步优化的必要。