基于快速自适应超螺旋算法的高速列车最优黏着控制

李中奇，张俊豪

(1.华东交通大学 电气与自动化工程学院，江西 南昌 330013；2.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013)

高速列车轮轨间黏着特性具有较高的非线性和时变性，轨面状态变化易导致机车牵引制动力得不到有效发挥。近年来许多国内外学者对此展开针对性研究，ZIREK等[1]提出了一种比例积分控制方法，为确定黏着曲线上的最优黏着系数提供参考。FANG等[2]提出了一种改进的黏着控制方法，用带遗忘因子的递推最小二乘法求得黏滑曲线的斜率。TORRES-ZUIGA等[3]提出了一种基于超螺旋的优化算法计算导致未知凸目标函数极值的输入。HE等[4]提出了一种基于最优蠕滑率的积分滑模防滑控制方法。ZHAO等[5]设计了一种基于滑模观测器(SMO)的智能黏着系数传感器，利用负载转矩观测值进一步计算轮轨黏着系数。HAJANO等[6]提出了一种基于模糊逻辑的城际列车防滑控制器。UYULAN等[7]提出鲁棒自适应控制策略，最大限度地提高再黏着过程后的黏着利用率。CHEN等[8]在车辆模型上增加不规则轨迹，采用递归最小二乘法确定车轮黏着状态，计算最佳制动力。李宁洲等[9]研究出一种基于自适应子群协作QPSO算法的机车黏着控制。徐传芳等[10]提出一种基于障碍Ly‐apunov函数的蠕滑速度动态面跟踪控制算法，但需要设定系统不确定性上界。马天和等[11]通过设计黏着力观测器对黏着力进行在线观测。王会议[12]提出一种基于模糊近似熵的黏着控制方法。魏银花等[13]提出一种云模型的黏着控制方法。赵凯辉等[14]将超螺旋算法应用于重载机车的黏着控制，取得较好的效果。超螺旋(Super-Tw isting,ST)算法是一种高阶滑模控制算法，算法在抑制抖振的同时还能保持对干扰的鲁棒性，提高控制精度。但算法有限时间稳定条件需要已知系统不确定性上界，实际应用中这个界的精确值很难确定，为得到系统的稳定控制，往往选取尽可能大的参数，结果带来系统损坏和剧烈抖振。刘畅等[15]在标准超螺旋算法上引入线性项和自适应控制器设计出快速自适应超螺旋(FastAdaptive Super-Tw isting,FAST)算法并成功应用于导弹制导律的设计。该算法不需要已知系统不确定性的边界且收敛速度较快。列车黏着控制系统为非线性系统且具有较强不确定性，考虑FAST算法对于非线性不确定系统具有较强鲁棒性，本文将FAST算法应用于列车黏着控制，并提出了一种新的滑模控制律，实现了最优黏着控制。

1 列车轮轨模型及黏着关系

1.1 轮对动力学模型

本文以CR400AF型高速列车(4M 4T)为研究对象，单轮对受力分析如图1所示。

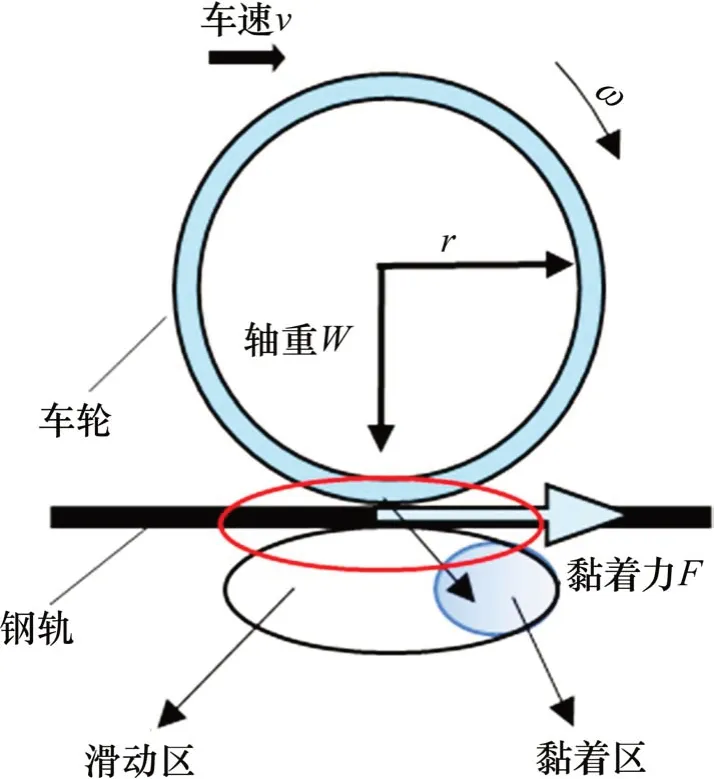
图1 单轮对受力分析Fig.1 Force analysisof singlewheel set

电机转矩方程：

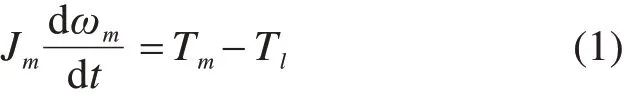
负载转矩Tl可由此求得：

其中：Fμ为黏着力，Rg为传动比。

黏着系数μ(vs)为：

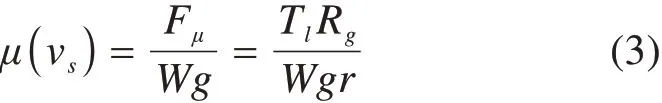
考虑转矩产生过程的列车动力学模型描述，忽略牵引电机与轮对间的转矩传输动态影响，车轮及车体的动态方程可以表示为：

式中：Fr为列车运行总阻力，在列车启动阶段，主要考虑列车运行基本阻力Fd。

式中：Jm为电机转动惯量，kg∙m2；ωm为电机角速度，rad/s；Tm为电机转矩，N∙m；Tl为负载转矩，N∙m；r为轮对半径，mm；W为列车轴重，t；M为整车重量，t；Fμ为机车黏着力；动轴数N=16；FN=NFμ为机车总黏着力；vt为车轮速度；vd为机车速度；a，b和c为基本阻力系数；g为重力加速度。

1.2 轮轨黏着特性分析

列车蠕滑速度为：

黏着系数与蠕滑速度之间的函数关系为[12]：

式中：a1，a2，a3为轨面系数，不同轨面系数如表1所示[14]。

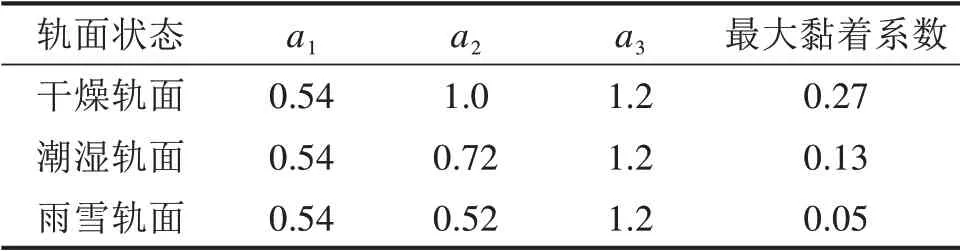
表1 不同轨面系数Table 1 Coefficientof different railsurface

不同轨面黏着特性曲线如图2所示。

图2 不同轨面黏着特性曲线Fig.2 Adhesion characteristic curvesof different railsurfaces

2 蠕滑速度搜索及控制器设计

2.1 全维状态观测器观测黏着系数

依据列车运行实际过程，电机角速度ωm可测，负载转矩Tl不可测，设计观测器对负载转矩进行观测，由式(1)和式(2)可得状态空间表达式如下

由状态方程可知系统具有完全能观性，采用极点配置方法设计全维状态观测器。

式(9)中p1，p2为待配置极点，通过极点配置使观测器收敛[14]，通过对不同极点的选取对比可知，当p1=-100,p2=100时，观测器动态响应更快，在轨面条件突然发生改变的情况下可以加快黏着控制系统的响应速度。得到负载转矩观测值如下：

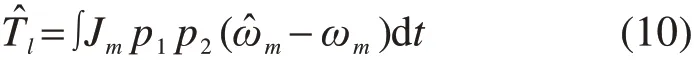
由式(3)可求得黏着系数估计值μ̂(vs)为：

2.2 滑模极值搜索算法搜索最优蠕滑速度

极值搜索是在闭环系统中自动寻找系统最优值，其主要用来实现动态系统的实时最优化。依据轮轨黏着曲线中黏着系数先增大后减小，并存在唯一极值的特点，将黏着系数观测值作为搜索算法的输入，搜索当前轨面蠕滑速度最佳估计值。原理如图3所示。

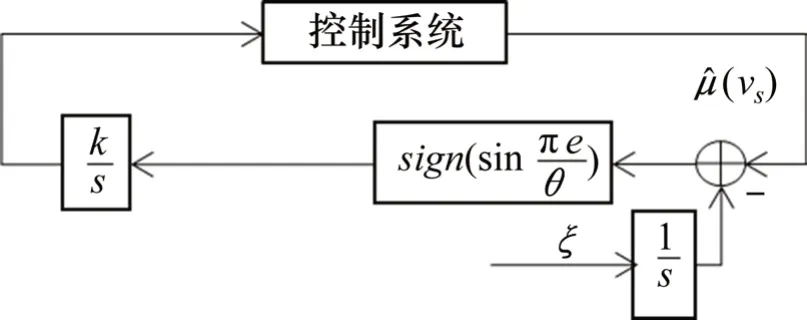
图3 滑模极值搜索原理Fig.3 Schematic of slidingmode extremum search

构造切换滑模面：

由搜索原理可知s(t)在任意初始条件下，均能在Nθ系列滑模面上收敛(N=0,±1,…)，保证了任意初值的滑模可达性。

2.3 控制系统设计

控制系统原理如图4所示，根据列车模型输出电机角速度至全维状态观测器得到黏着系数，极值搜索部分搜索最佳蠕滑速度，将最佳蠕滑速度与其导数输入控制器得到控制转矩，完成黏着控制的闭环控制。

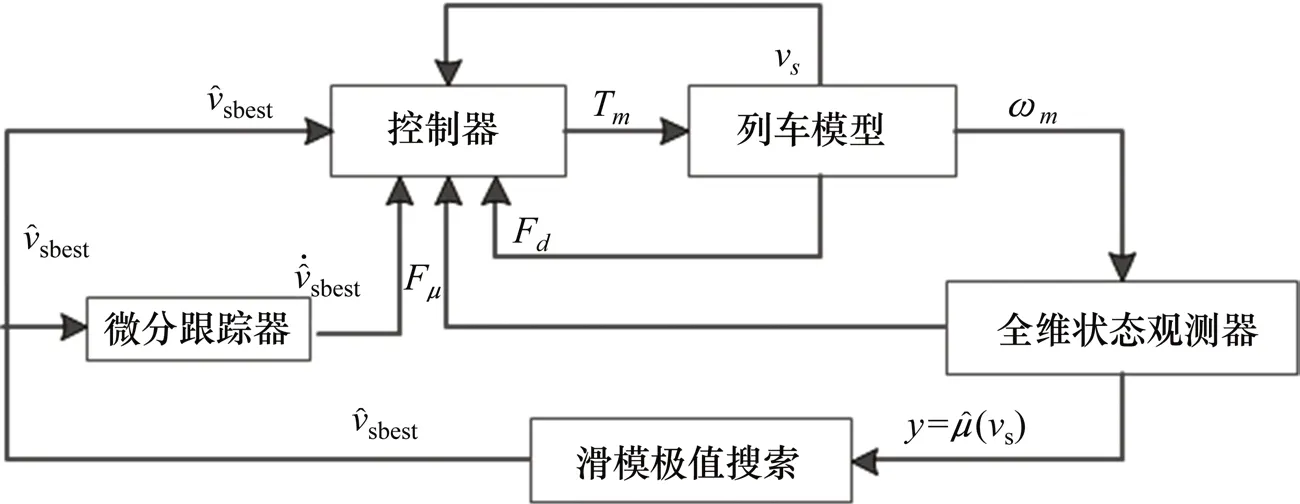
图4 控制系统原理Fig.4 Controlsystem schematic

根据式(4)轮对动力学模型和式(5)列车运动方程，设状态变量x=vt-vd=vs，可得列车模型：

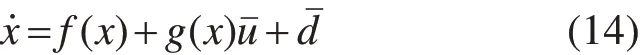
定义滑模面s为：

式中：vsbest是极值搜索算法搜索到的当前轨面的最优蠕滑速度，将式(4)，(5)，(7)代入式(16)得：

2.3.1 超螺旋滑模控制律设计

针对式(14)，可将其考虑为1阶系统：

u∊R为控制输入，H∊R为不确定项。根据超螺旋滑模控制原理，设计控制律为：

式中：ueq为滑模控制项：udc为滑模切换项，k1,k2为待设计参数。

设计等效滑模控制律ueq为：

根据超螺旋滑模控制器原理[14]和式(21)得到控制律为：

式中：k1,k2为人为选定使得系统稳定的控制器参数，k1=4,k2=3。

2.3.2 快速自适应超螺旋滑模控制器设计

定义系统(18)中，不确定项H=H1(x,t)+H2(x,t)，H1(x,t)表示系统不可微的不确定性，H2(x,t)表示系统可微的不确定性。

设H1(x,t)和H2(x,t)满足：

式中：g1和g2为未知正数；ϕ1(x)和ϕ2(x)为滑模变量函数。

控制律设计如下：

式中：

自适应参数控制器为：

式中：a,b,c,d为正数。

由于滑模面很难完全收敛至0，是在0的极小邻域内波动，从而会导致k1,k2过大，引起系统不稳定。因此，将自适应参数控制器改进为

式中：λ为极小正数。

根据式(22)和(25)，设计快速自适超螺旋滑模控制律如下：

其中：k1,k2满足下式

式中参数满足：a∊[5,10],b∊[5.5,6],c=d=1。

由式(29)可以看出控制器参数k1,k2随滑模面s变化而改变，实现了自适应调节。

2.3.3 快速自适应超螺旋滑模控制器稳定性证明

令ρ1=H1(x,t),ρ2=H2(x,t)，将 式(24)代 入 系统，得到控制系统为：

可得

式中：ε1为足够小的正常数，结合可得：

因此：

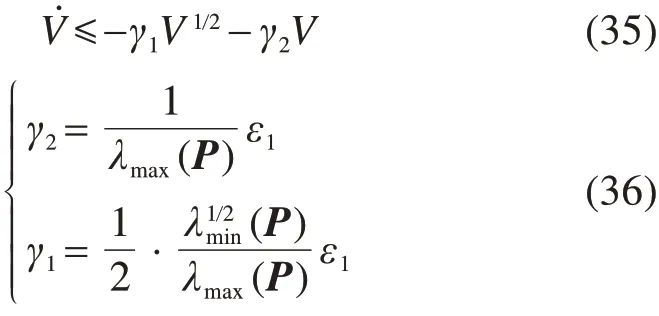
所以当ξT=[ϕ1(x1),x2]，在有限时间内收敛到0，且收敛时间满足

当参数k1和k2满足式(30)条件时，x1和在有限时间treach内收敛到0。

3 仿真分析

参数设置参考CR400AF参数如表2。

表2 列车相关参数Table 2 Train parameters

轨面条件设定，0～30 s：干燥轨面，30～50 s：潮湿轨面，50～70 s：干燥轨面。

3.1 最佳蠕滑速度搜索对比

图5为不同控制算法下的蠕滑速度搜索结果，由图可知传统滑模控制算法搜索效果较差，而ST算法和FAST算法搜索结果良好，轨面变化时，系统始终能够快速搜索到最佳蠕滑速度。由局部放大图可知，ST算法下，系统搜索到的蠕滑速度在1.2～2m/s之间，波动幅度较大；而FAST算法下，蠕滑速度稳定在1.4～1.5m/s之间。FAST算法在不同轨面最佳蠕滑速度搜索值的精度、收敛性都比ST算法有着更好效果。

图5 蠕滑速度对比Fig.5 Comparison of creep speed

3.2 黏着系数观测对比

图6为不同控制算法下轨面黏着系数的观测结果，0～1 s，列车启动阶段，黏着系数观测值剧烈振荡。由局部放大图可知，传统滑模控制算法观测效果不佳，而且抖振较大，ST和FAST算法观测效果良好，且FAST算法在线观测的轨面黏着系数抖振小，收敛速度快，在5 s处黏着系数到达0.267，将稳定时间缩短了5 s。

图6 黏着系数对比Fig.6 Comparison ofadhesion coefficient

3.3 控制转矩对比

由图7可知，各算法的控制转矩与轨面变化趋势一致，0～30 s转矩稳定在67 200 N∙m，30～50 s转矩稳定在32 720N∙m，50 s后控制转矩重新稳定在67 200 N∙m临域内。由局部放大图可知，传统滑模控制算法控制精度不高，抖振剧烈，后2种算法在转矩控制速率和精度上都有所提高，且FAST算法收敛时间更短，抖振更小，轨面切换时转矩变化更平稳。

图7 控制转矩对比Fig.7 Comparison of control torque

3.4 控制器鲁棒性对比

为验证控制器的鲁棒性，在列车模型中加入随机序列干扰，加入干扰后的列车模型为：

图8为在2种较好控制算法下的输出转矩相对误差对比。初始阶段FAST算法能快速稳定；稳定运行后，由局部放大图可知，系统受到干扰后FAST算法设计的控制器输出转矩相对误差更小接近零值，控制器具有更好的鲁棒性。

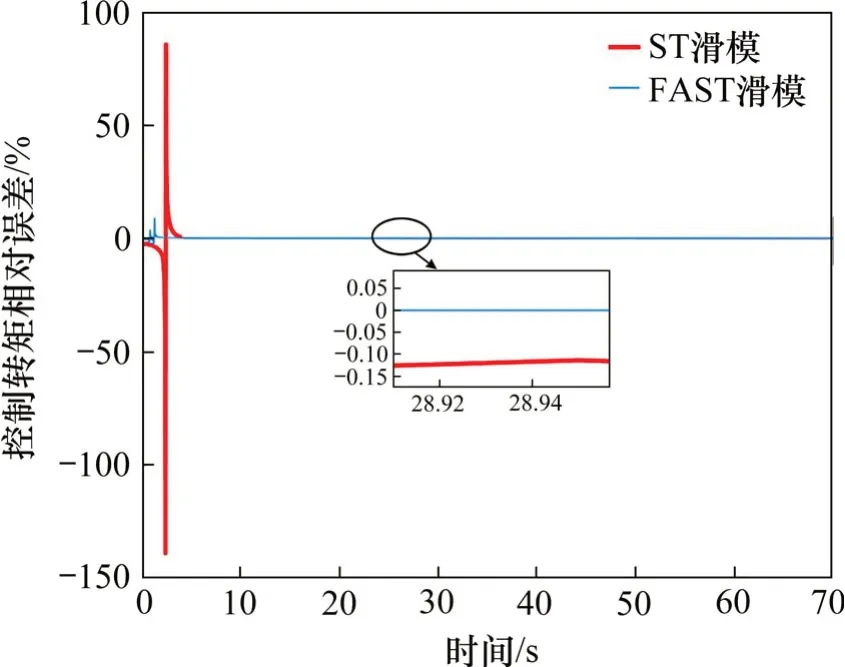
图8 控制转矩相对误差对比Fig.8 Comparison of control torque relative error

4 结论

1)与ST算法相比，FAST算法在系统的不确定性上界未知的情况下，控制器参数实现了自适应调节，解决了人为调节控制器参数过大造成系统不稳定的问题。

2)在超螺旋滑模算法基础上进一步抑制抖振并增强控制器鲁棒性，并具有快速收敛的特性，使得黏着控制更快速、稳定、安全。

3)本文验证了FAST算法的可行性与优越性，下一步将以此为基础对高阶滑模算法和列车运行的速度跟踪控制进行深入研究。