基于不同速度控制模式的列车驾驶策略优化研究

李蔚，刘高峰，赵思哲，于晓泉,2，韩锟，李茜

(1.中南大学 交通运输工程学院，湖南 长沙 410075；2.北京全路通信信号研究设计院集团有限公司，北京 100070)

优化列车驾驶策略(列车速度曲线)可以降低列车运行过程中的牵引能耗。列车的节能运行对铁路网络的节能减排有促进作用，进一步可以促进“碳达峰、碳中和”目标的实现。列车运行能耗主要包含辅助能耗和牵引能耗2个部分：辅助能耗由列车的非牵引设备产生，其功率大小确定；牵引能耗由列车的牵引设备产生并用以驱动列车行驶，占列车总运行能耗的70%以上[1]。列车的牵引能耗与列车速度曲线有关，具有一定的优化空间。列车驾驶策略优化问题最早由日本学者ICHIKAWA在20世纪60年代提出，该研究考虑平直线路并利用庞特里亚金极大值原理对问题进行了分析，指出了列车节能驾驶策略包含最大牵引、巡航、惰行和最大制动4种节能运行工况[2]。ICHIKAWA的研究吸引了很多学者的研究兴趣，并使得这一研究领域在过去几十年得到发展。优化列车驾驶策略的主要方法分为解析方法、数值方法和元启发式算法3类。在M ILROY[3]研究的基础上，AL‐BRECHT等[4-5]及其团队对列车驾驶策略优化问题进行了一系列研究，采用的方法以解析方法为主。HOWLETT团队的ALBRECHT后来对列车驾驶策略优化问题进行了总结，这些研究成果成为列车驾驶策略优化的早期理论基础。优化列车驾驶策略的数值方法以动态规划为代表，但动态规划存在因状态空间增大导致求解时间过长的问题。针对该问题，高豪等[6]提出了基于动态规划的快速优化方法，但该方法优化列车驾驶策略的求解过程依旧较复杂。元启发式算法在列车驾驶策略优化问题上被使用最多[7]，其无需目标函数梯度信息的寻优特性吸引更多学者利用元启发式算法优化列车驾驶策略。CHANG等[8]利用遗传算法对列车惰行点进行寻优，充分利用列车惰行工况以降低列车牵引能耗。LU等[9]采用了蚁群优化算法、遗传算法和动态规划，考虑不同优化算法的寻优特性设置了不同的建模求解规则，分别优化了列车速度曲线并对比分析了3种算法的优化性能；该研究存在对优化算法寻优特性依赖程度高和不同优化算法求解规则设置复杂的问题，可能导致算法的优化性能表现受建模求解过程的影响。元启发式算法中的群智能优化算法也多被用来求解列车驾驶策略优化问题，并取得了一定的节能效果[10-12]。在问题分类上，连续速度控制模式或离散速度控制模式是列车驾驶策略问题的2个基本分类[13]。已有研究虽然采用了不同类别的优化方法优化列车驾驶策略，但主要针对单一速度控制模式进行优化和对比，较少有文献对比分析相同条件下2种速度控制模式的列车节能速度曲线节能效果差异[13]。此外，已有研究中列车驾驶策略的优化过程过度依赖特定算法的寻优特性，导致问题建模过程复杂，很难采用多种优化算法基于统一的模型和基准进行横向对比。基于以上研究现状，本文提出2种速度控制模式的列车驾驶策略多目标优化方法，同时提出2种速度控制模式下列车驾驶策略优化的优化算法决策变量通用设置规则。考虑不同的区间运行时间方案，基于提出的列车驾驶策略多目标优化方法及其对应的优化算法决策变量通用设置规则，在2种线路条件上分别采用粒子群优化、模拟退火和模式搜索法优化列车节能速度曲线，对比分析2种速度控制模式列车节能速度曲线的节能效果。本研究分析了2种速度控制模式列车节能速度曲线在不同运行时间和不同线路条件下的节能效果并给出相应结论，对后续研究具有一定的参考意义。本文所提出的优化算法决策变量通用设置规则解决了已有研究中优化列车驾驶策略过度依赖特定算法寻优特性的问题，具有更好的通用性。

1 问题建模

列车速度曲线的生成及优化需要对列车运行过程进行建模分析。下面，将对列车运行过程进行分析，并建立列车区间运行多目标优化数学模型。

1.1 列车牵引计算

列车运行时，一般用如下公式[14]描述列车运行过程：

其中：v是列车运行速度；x是列车当前位置；F(v)是与列车牵引特性相关的牵引力，kN；B(v)是与列车制动特性相关的制动力，kN；W0(v)是与列车运行速度有关的基本阻力，kN；Wi(x)是与线路条件有关的附加阻力(坡道附加阻力、隧道附加阻力和曲线附加阻力)，本文仅考虑坡道附加阻力，kN；ρ是列车回转质量系数，与列车特性有关；M为列车质量，t。

列车牵引力F和制动力B根据列车的牵引特性曲线和制动特性曲线确定，也可以采用经验公式法。

根据铁道行业技术标准[15]，列车运行所受基本阻力计算公式如下：

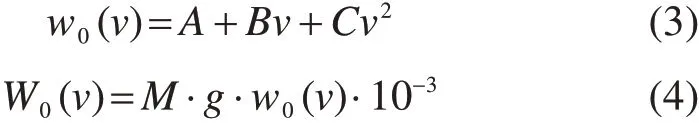
式(3)中：w0为单位基本阻力，N/kN；A，B和C为经验系数，通常给定；常数项A和线性项Bv是与列车质量有关的列车滚动阻力；二次项Cv2是与列车质量无关的列车空气阻力。

式(4)中，W0为列车运行所受基本阻力，kN；g为重力加速度。

根据铁道行业标准[15]，单位坡道附加阻力的计算公式如下：

式(5)中：wi为单位坡道附加阻力，N/kN；i为坡道的坡度千分数，取上坡为正值。

列车所受坡道附加阻力的计算公式如下：

由式(6)可知，Wi与列车的质量有关，kN。

1.2 列车节能运行工况

在列车驾驶策略优化问题中，采用列车节能运行工况描述列车运行状态，因为列车在节能运行工况下最节能[2]。按照线路的坡度变化情况，列车节能运行工况有所不同。水平线路上，列车节能运行工况有最大牵引(Maximum Acceleration,MA)、巡航(Cruising,CR)、惰行(Coasting,CO)和最大制动(Maximum Braking,MB)4种[2]；变坡度线路上，除了水平线路上的4种节能运行工况，还有列车在下陡坡区段维持巡航的部分制动工况(Partial Braking,PB)[16]。PB运行工况在速度表现形式上与CR运行工况相同，都是维持列车在一定速度运行；不同之处在于PB运行工况下列车施加部分再生制动力来克服列车在下陡坡区段受到的与列车前进方向相同的总运行阻力，而CR运行工况下列车施加部分牵引力来克服列车受到的与列车前进方向相反的总运行阻力。因此，CR运行工况下牵引电机消耗电能，而PB运行工况下四象限变流器利用再生制动技术反馈电能。在后文中，以CR运行工况统称维持列车巡航的CR运行工况和PB运行工况，但在计算列车能耗时加以区分。

1.3 列车区间运行的多目标优化数学模型

在本研究中，主要考虑准点性、节能性和站停准确性，并作为3个量化的优化目标。定义这3个优化目标：准点性，表示为列车区间给定运行时间Tgiven与列车区间运行时间T的误差，定义为obj1=|Tgiven-T|；节能性，表示为列车区间运行能耗E，定义为obj2=E；站停准确性，表示为区间距离Ssection与列车速度曲线运行距离S的误差，定义为obj3=|Ssection-S|。

除了3个优化目标，列车区间运行多目标优化还需满足一定的现实约束。列车区间运行多目标优化的数学模型如下：

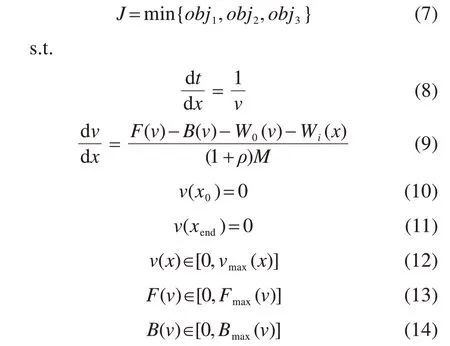
式(10)和式(11)中的x0和xend分别为区间起点和区间终点；式(12)，式(13)和式(14)中的vmax(x)，Fmax(v)和Bmax(v)分别表示线路限速约束、最大牵引力约束和最大制动力约束。

2 不同速度控制模式的列车驾驶策略多目标优化方法

2.1 列车驾驶策略多目标优化的参考基准

2.1.1 列车运行时间与列车运行能耗的关系

列车驾驶策略优化本质上是一个需要满足多种现实约束的多目标优化问题。多目标优化问题中，不同优化目标往往矛盾，需在优化过程中进行取舍。运行时间与运行能耗是列车驾驶策略优化问题的2个主要优化目标，两者关系见图1。图1所示曲线为2个优化目标之间的关系，一些文献也称之为Pareto前沿曲线[13]或成本-时间曲线(costtime curve)[17]。

图1 列车运行时间与列车运行能耗之间的关系Fig.1 Relationship between train running time and train energy consumption

受限于列车最大牵引力、列车最大制动力、线路限速和线路坡度等约束条件，列车在区间运行存在一个技术性的最短运行时间。列车区间冗余运行时间，定义为区间给定运行时间与列车区间最短运行时间之差。列车区间冗余运行时间的多少可以揭示通过延长列车区间运行时间ΔT来降低列车区间运行能耗ΔE的优化潜力，见图1。通过生成列车区间最速曲线，可以求得具体列车在特定区间线路上的区间冗余运行时间。区间冗余运行时间越多，则列车驾驶策略可节能优化的空间越大。已有研究[18]提出了一种两阶段优化方法对列车区间冗余运行时间进行分配及优化，通过实例分析验证了优化方法的节能效果。列车区间最速曲线对应的性能指标(区间最短运行时间和区间最高运行能耗)将作为本文中列车驾驶策略多目标优化的参考基准。

2.1.2 列车区间最速曲线的生成方法

列车区间最速曲线的运行工况切换序列为MA-CR-MB。在区间线路距离固定的情况下，该运行工况切换序列的列车区间平均速度最高，因此列车区间运行时间最短。MA-CR-MB切换序列中的2个切换点无需优化，但需要根据列车数据和线路数据计算求得。列车区间最速曲线的求解步骤如下。

输入：列车数据(固定参数、牵引特性、制动特性和基本阻力等)，路数据(线路长度、坡度数据和限速数据)。

Step 1从区间起点，根据列车固定参数和牵引特性，计算列车MA运行工况下从0到运营速度的最短牵引距离；

Step 2从区间终点，根据列车固定参数、制动特性和列车制动初始速度，反向递推计算列车MB运行工况下到站停车的制动初始点；

Step 3列车MA运行工况终点到MB运行工况起点之间的区间中间线路，在满足线路限速约束下，列车采用CR运行工况维持限速运行；

Step 4计算得到列车区间最短运行时间和列车区间最高运行能耗；

Step 5绘制列车区间最速曲线的列车运行速度-距离关系图；

Step 6绘制列车区间最速曲线的列车所受合力-距离关系图。

输出：列车区间最速曲线及其对应的列车所受合力变化图。

2.2 面向连续控制的列车驾驶策略多目标优化

2.2.1 连续速度控制模式的列车运行工况切换序列

连续控制型和离散控制型是列车驾驶策略优化问题的2种基本类型[13]，依据对列车速度控制变量(牵引力或制动力)的控制类型而划分。连续控制模式意味着列车节能运行工况中存在CR运行工况和PB运行工况，即列车可以实时调整连续的控制变量(列车牵引力或列车再生制动力)以维持列车在当前速度行驶。对于连续控制模式，列车可以在水平线路或上坡道实时调整部分牵引力以克服列车受到的向后的总运行阻力使得列车所受合力为0，或者列车可以在下陡坡调整部分再生制动力以克服列车受到的向前的总运行阻力使得列车所受合力为0。对于自动驾驶列车，采用闭环控制算法可以实时调整列车的部分牵引力或部分再生制动力，以使列车巡航运行。

对于连续控制模式，已有研究指出了列车运行工况最优切换序列为MA-CR-CO-MB[18]。确定了连续控制模式的运行工况最优切换序列，剩下只需要利用优化算法寻找运行工况最优切换点。

2.2.2 优化算法决策变量的通用设置规则

通过预先确定列车运行工况切换序列，可以将列车驾驶策略优化问题从组合优化及连续优化问题转换成单一的连续优化问题，有效降低了问题的求解时间。具体来说，就是将列车节能速度曲线中的运行工况切换序列预先确定，优化变量便只剩下不同节能运行工况之间的运行距离这一连续变量。在连续控制模式下，优化过程的决策变量为运行工况切换序列MA-CR-CO-MB之间的切换点，也可以表示为每个节能运行工况的运行距离，表示如下：

需要指出的是，本文对于列车制动距离的计算采用反向递推的方法。根据区间线路终点位置和列车制动初始速度计算列车的制动起点位置，即MB运行工况起点。采用反向递推计算的原因在于列车制动终点的位置(区间终点)和速度(0)已知，而制动初始速度不固定，所以需要反向递推计算制动起点位置(MB运行工况作用距离)。因此，在决策变量中无需设置MB运行工况的作用距离，求解模型将反向递推计算MB工况作用距离。

2.2.3 连续控制型列车驾驶策略多目标优化方法

基于MA-CR-CO-MB的运行工况最优切换序列，本文提出一种连续控制型列车驾驶策略的多目标优化方法，具体步骤如下。

输入：列车参数(固定参数、牵引特性、制动特性和基本阻力等)、线路数据(线路长度、坡度数据和限速数据)。

Step 1初始化优化目标obj1，obj2和obj3；

Step 2初始化决策变量XC；

Step 3调用优化算法根据优化目标和约束条件优化决策变量XC；

Step 4根据决策变量XC，反向递推计算列车制动距离xMB；

Step 5求得运行工况最优运行距离XC′=[xMAxCRxCOxMB]；

Step 6计算优化后列车节能速度曲线的区间运行时间、区间运行能耗和区间运行距离；

Step 7绘制连续控制型列车节能速度曲线的列车运行速度-距离关系图；

Step 8绘制连续控制型列车节能速度曲线的列车所受合力-距离关系图。

输出：连续控制型列车节能速度曲线及其对应的列车所受合力变化图。

2.3 面向离散控制的列车驾驶策略多目标优化

2.3.1 离散速度控制模式的列车运行工况切换序列

离散速度控制模式，意味着列车速度的控制变量(列车牵引力和制动力)是非连续的，即列车不能实时调整牵引力或再生制动力的大小以使列车所受合力为0，从而保持巡航状态。离散速度控制模式下，列车节能运行工况为MA，CO和MB 3种。虽然人工驾驶列车的司机室设置了不同级别的牵引操纵手柄位和制动操纵手柄位，但文献[2,16,18]已经证明除了MA，CR，CO和MB的其他运行工况均非节能运行工况。因此，离散速度控制模式下的列车驾驶策略需要采用MA-CO工况对的组合来替代连续速度控制模式的运行工况最优切换序列MA-CR-CO-MB中的CR工况。

关于MA-CO工况对数量的选取，需要参考多方面的因素。首先，HOWLETT在理论上证明了MA-CO工况对越多越节能[19]；但在实际运行过程中，列车工况频繁切换将降低旅客乘坐舒适度，并造成不必要的能耗损失。综合考虑，本文依据线路坡道的坡度特征进行划分并确定MA-CO工况对的数量，再利用优化算法的寻优过程来找到最优的MA-CO作用距离。《高速铁路设计规范》规定正线坡段的最小长度一般条件下不少于900m，困难条件下不少于600m[20]。同时，《高速铁路设计规范》规定了不同坡度下的坡段最大长度：15‰的坡度时不大于10 km；20‰的坡度时不大于6 km；30‰的坡度时不大于4 km[21]。

综合考虑以上因素，本文将根据区间线路长度设置MA-CO工况对数量，再设置MA-CO工况对决策变量的下边界为600m；为了充分发挥优化算法的连续优化特性，设置上边界为比10 000m长的50 000m。MA-CO工况对的下边界代表MA工况或CO工况的最小切换间隔，即工况最短运行距离；MA-CO工况对的上边界代表MA工况或CO工况的最大持续距离。在上下边界之间，利用优化算法的连续优化特性寻优得到MA工况或CO工况的最优作用距离，即MA-CO工况对的最优切换点。

2.3.2 优化算法决策变量的通用设置规则

在离散控制型列车驾驶策略优化中，优化过程的决策变量为除MB运行工况外的运行工况切换点，也可以表示为每个运行工况的作用距离，表示如下：

式(16)中：p表示MA-CO工况对的数量，依据上一小节中的原则确定。

基于上述的优化算法决策变量通用设置规则，在满足决策变量上下边界的条件下，可以采用不同的优化算法优化不同运行工况的作用距离。本文提出的优化算法决策变量通用设置规则降低了优化过程对特定算法寻优特性的依赖程度，同时降低了问题的建模难度，具有更强的通用性。

2.3.3 离散控制型列车驾驶策略多目标优化方法

基于MA-(MA-CO工况对)-CO-MB的运行工况最优切换序列，给出离散控制型列车驾驶策略的多目标优化方法，具体步骤如下。

输入：列车参数(固定参数、牵引特性、制动特性和基本阻力等)、线路数据(线路长度、坡度数据和限速数据)。

Step 1初始化优化目标obj1，obj2和obj3；

Step 2依据线路长度和线路坡度特征划分MACO工况对的数量p；

Step 3初始化决策变量XD，设置MA-CO工况对的决策变量边界为[600,50 000]；

Step 4调用优化算法根据优化目标和约束条件优化决策变量XD；

Step 5根据决策变量XD，反向递推计算列车制动距离xMB；

Step 6求得运行工况最优运行距离XD′=

Step 7计算优化后列车节能速度曲线的区间运行时间、区间运行能耗和区间运行距离；

Step 8绘制离散控制型列车节能速度曲线的列车运行速度-距离关系图；

Step 9绘制离散控制型列车节能速度曲线的列车所受合力-距离关系图。

输出：离散控制型列车节能速度曲线及其对应的列车所受合力变化图。

3 实例分析与讨论

基于本文提出的2种速度控制模式下列车驾驶策略多目标优化方法及其对应的优化算法决策变量通用设置规则，分别采用3种优化算法进行优化。粒子群优化(Particle Swarm Optim ization,PSO)是一种全局随机并行搜索的群智能优化算法，其灵感来自于鸟类的觅食行为；模拟退火(Simulated Annealing,SA)是一种基于概率的通用优化算法，其灵感来自于冶金学中的退火过程；模式搜索(Pattern Search,PS)是一种求解多维最优化问题的局部搜索算法，每次迭代搜索都交替进行轴向移动和模式移动，以期望使迭代序列逼近极小值点。

仿真所用实验平台：Windows 10 64位操作系统、Intel®CoreTMi5-8300H中央处理器、NVIDIA GeForce GTX 1060显卡、16 GB内存和MATLAB R2020b。

3.1 列车实例和线路实例

本文选用CRH3C型动车组列车作为仿真实例，具体列车参数见表1。

表1 CRH3C型动车组列车主要参数Table 1 Main parametersof CRH3C EMU train

本文的线路实例采用岳阳东站(公里标K1440+000)到汨罗东站(公里标K1510+085)长70 085m的区间线路，线路限速300 km/h。查询铁路12306官网(http://www.12306.cn)的列车运行时刻表，岳阳东站到汨罗东站的运行车次见表2。可知区间给定运行时间有19 m in(1 140 s)和20 m in(1 200 s)2种方案。

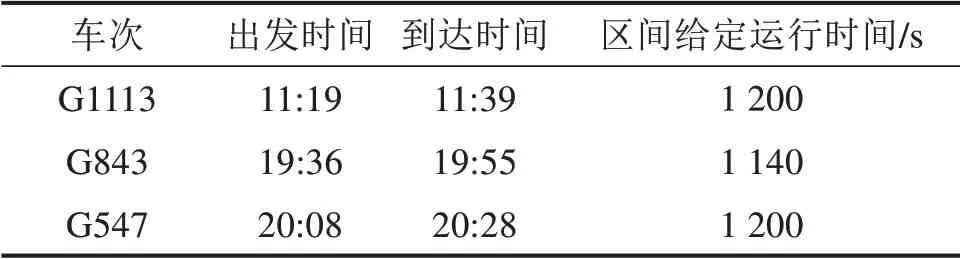
表2 2022年3月28日岳阳东站到汨罗东站的运行车次Table 2 Trains running from Yueyangdong Station to M iluodong Station on M arch 28,2022

图2展示了岳阳东站到汨罗东站区间线路坡度变化情况。可以发现，该区间线路存在7个上坡道和6个下坡道。上坡道和下坡道的最大坡度均不超过20‰，符合《高速铁路设计规范》[20]。

图2 岳阳东站到汨罗东站的区间线路坡度Fig.2 Slope of the interval line from Yueyangdong Station to M iluodong Station

3.2 连续控制型列车节能速度曲线

基于本文提出的方法，生成了CRH3C型动车组列车从岳阳东站到汨罗东站的区间最速曲线和2种区间运行时间方案下的连续控制型列车节能速度曲线，见图3。

图3(a)和图3(b)中列车区间最速曲线的运行工况切换序列为MA-CR-MB。对比分析图3(a)和图3(b)，可以发现1 200 s区间运行时间方案下的列车CO运行工况起点提前，同时CO运行工况平均速度更低，两者共同作用下列车区间运行时间从1 140 s延长到1 200 s。图3(a)和图3(b)中3种优化算法求得的连续控制型列车节能速度曲线仅在CO运行工况起点处存在部分差距，说明3个优化算法的优化性能差距较小且都接近或达到全局最优解。此外，图3(a)和图3(b)中的列车速度曲线在出站加速阶段出现了降速的现象，而在CO运行工况下出现了升速的现象，这是坡道附加阻力对列车所受合力的影响。为了体现坡道附加阻力影响，图4给出图3中列车速度曲线对应的列车所受合力变化。

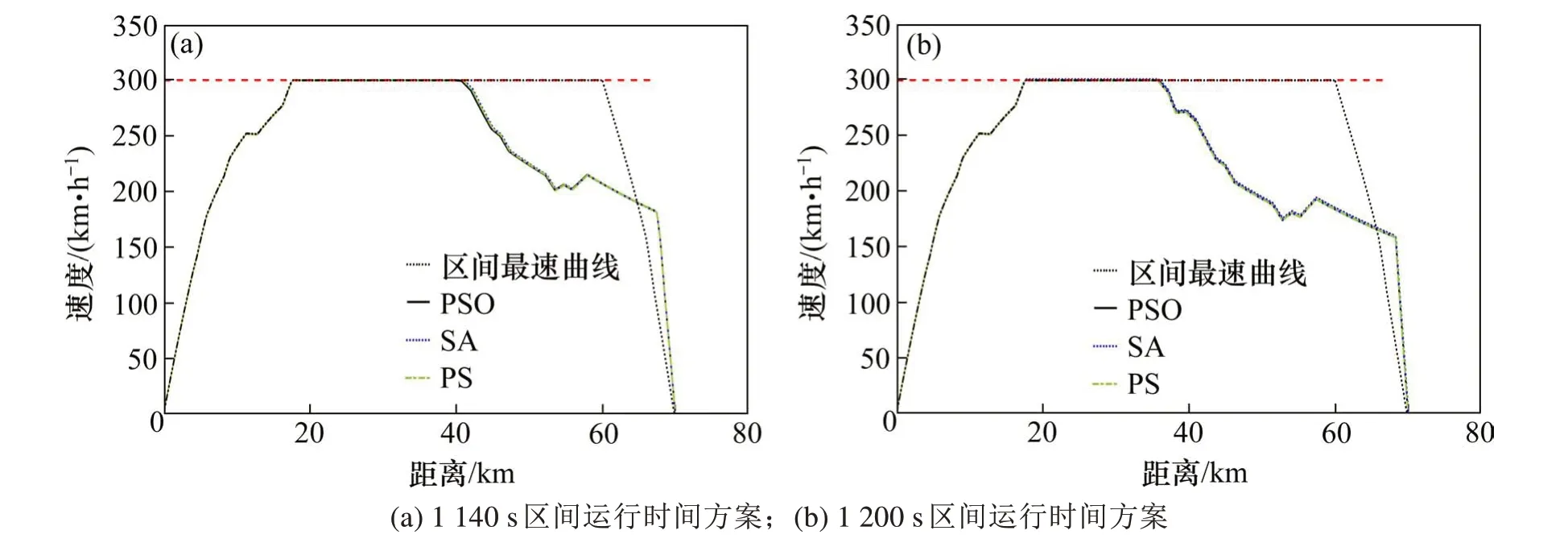
图3 列车区间最速曲线和3种连续控制型列车节能速度曲线Fig.3 Fastest train speed profile and the three energy-efficient train speed profilesw ith continuous control

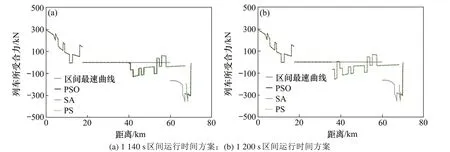
图4 图3中列车速度曲线的列车所受合力变化情况Fig.4 Variation of the combined force on the train for the train speed profiles in Fig.3

观察图4，可以发现列车所受合力在MA工况、CO工况和MB工况均出现了陡增或陡降的情况。对比图2和图4，可以发现：列车运行在下坡道时，列车所受合力陡增，列车受到向前的合力增加；列车运行在上坡道时，列车所受合力陡降，列车受到向后的合力增加。观察图4，可以发现图4(b)中的CO运行工况列车所受合力变化趋势比图4(a)中的CO运行工况所受合力变化趋势提前，与图3一致。

列车速度曲线体现了列车运行速度与列车运行距离的对应关系，而评价列车速度曲线的优劣则需要参考列车速度曲线对应的性能指标。图3中不同列车速度曲线的性能指标见表3。

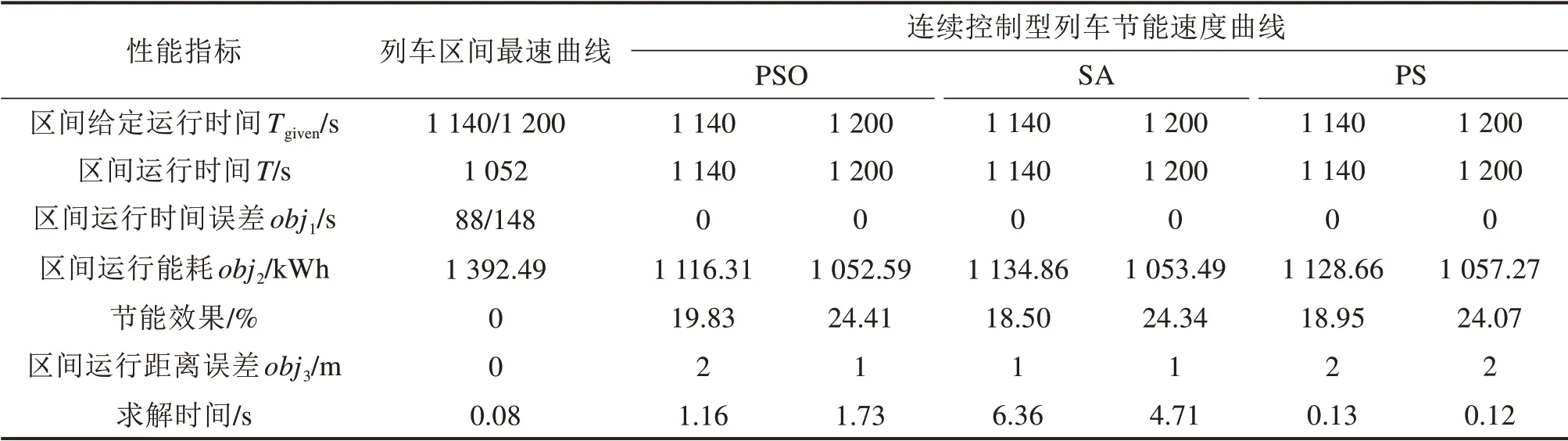
表3 连续控制型列车节能速度曲线的性能指标Table 3 Performance indicators forenergy-efficient train speed profilesw ith continuous control

分析列车区间最速曲线，可以发现：列车区间最短运行时间为1 052 s，低于区间给定运行时间1 140 s和1 200 s；列车区间最高运行能耗为1 392.49 kWh，将作为优化的参考基准。分析区间运行时间误差和区间运行距离误差，可以发现所有列车节能速度曲线均收敛。对比2种区间运行时间方案，可以发现1 200 s方案的列车区间运行能耗整体低于1 140 s方案的列车区间运行能耗。对比同一区间运行时间方案下的不同算法优化性能，可以发现PSO的节能效果均优于SA和PS。在求解时间上，求解时间最快的是PS，最慢的是SA，且所有算法的求解时间均不超过7 s。

3.3 离散控制型列车节能速度曲线

基于本文提出的离散控制型列车驾驶策略多目标优化方法及其对应的优化算法决策变量通用设置规则，采用PSO，SA和PS求得CRH3C型动车组列车从岳阳东站到汨罗东站的离散控制型列车节能速度曲线，见图5。其中，MA-CO工况对数量p设为8。

观察图5(a)和图5(b)，可以发现列车节能速度曲线之间的差异较为明显。图5(b)中列车节能速度曲线在线路中间的平均运行速度更低，实现了列车区间运行时间从1 140 s到1 200 s的延长。

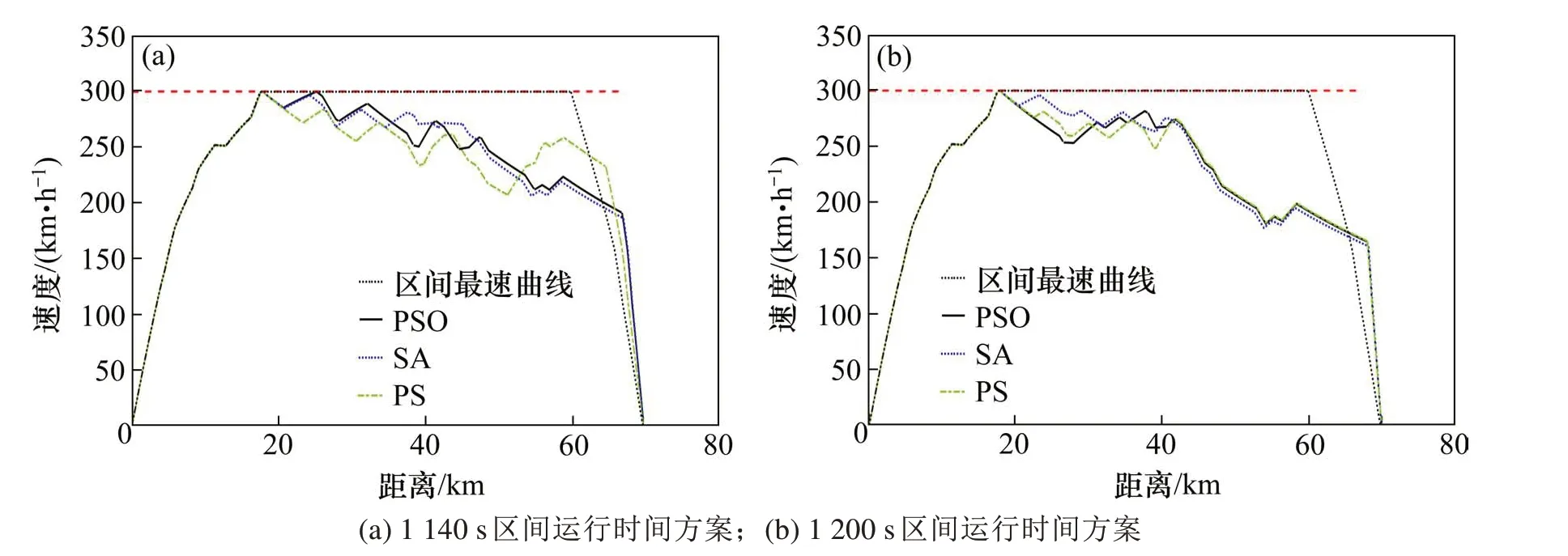
图5 列车区间最速曲线和3种离散控制型列车节能速度曲线Fig.5 Fastest train speed profile and the three energy-efficient train speed profilesw ith discrete control

图5(a)和图5(b)中的列车节能速度曲线同样受到坡道附加阻力影响从而呈现不光滑。图5中列车速度曲线对应的列车所受合力变化情况见图6。

观察图6，可以发现2种区间运行时间方案下的列车所受合力在运行全程均出现因坡道附加阻力造成的波动。下面给出3种离散控制型列车节能速度曲线的性能指标，见表4。

图6 图5中列车速度曲线的列车所受合力变化情况Fig.6 Variation of the combined force on the train for the train speed profiles in Fig.5

分析表4中的区间运行时间误差和区间运行距离误差，可以发现所有列车节能速度曲线均收敛。同样的，1 200 s区间运行时间方案的列车区间运行能耗整体低于1 140 s区间运行时间方案的列车区间运行能耗。在每种区间运行时间方案下，PSO的节能优化性能均优于SA和PS。3种优化算法的求解时间相较于连续控制型均有所增加，其中最快和最慢的依旧分别是PS和SA。

对比表3和表4，综合分析连续控制型列车节能速度曲线和离散控制型列车节能速度曲线的优化效果。在相同的区间运行时间方案和优化算法条件下，连续控制型列车节能速度曲线的节能效果均优于离散控制型列车节能速度曲线。分析线路条件，其原因在2个方面：岳阳东站到汨罗东站的区间线路中存在6个下坡道；连续速度控制模式下列车在下坡道施加部分再生制动力维持巡航，再生制动技术能够减少列车运行能耗。

表4 离散控制型列车节能速度曲线的性能指标Table 4 Performance indicators for the energy-efficient train speed profilesw ith discrete control

离散速度控制模式下，列车的节能运行工况中不包含CR运行工况和PB运行工况，而是以MA-CO运行工况对的组合在区间线路中间运行。对比列车在下坡道采用PB运行工况反馈制动动能，MA-CO工况对组合只能减少MA运行工况下的牵引能耗和增加CO工况的惰行距离进行节能，节能效果相对较低。为了对比实验，下面进行水平线路上的2种速度控制模式列车驾驶策略优化，水平线路上不存在PB运行工况。

3.4 水平线路上的列车节能速度曲线

图3和图5所示的列车节能速度曲线均考虑坡道附加阻力影响，因此出现了加速阶段降速和惰行阶段升速的现象。通过去除坡道附加阻力的影响，可以得到列车运行在水平线路上的列车区间最速曲线、连续控制型列车节能速度曲线和离散控制型列车节能速度曲线，见图7。

可以发现，不同运行时间的列车速度曲线在MA工况和CO工况时的速度曲线均是光滑的，未出现加速阶段降速和惰行阶段升速的现象。图8展示了图7中列车速度曲线对应的列车所受合力变化情况。

图7 水平线路上的3种列车速度曲线Fig.7 Three train speed profilesof the train running on the level track

观察图8，可以发现列车区间运行全程都未出现因坡道附加阻力而产生的波动，说明列车未受到坡道附加阻力影响。进一步分析水平线路上2种速度控制模式列车节能驾驶策略的节能效果，见表5。

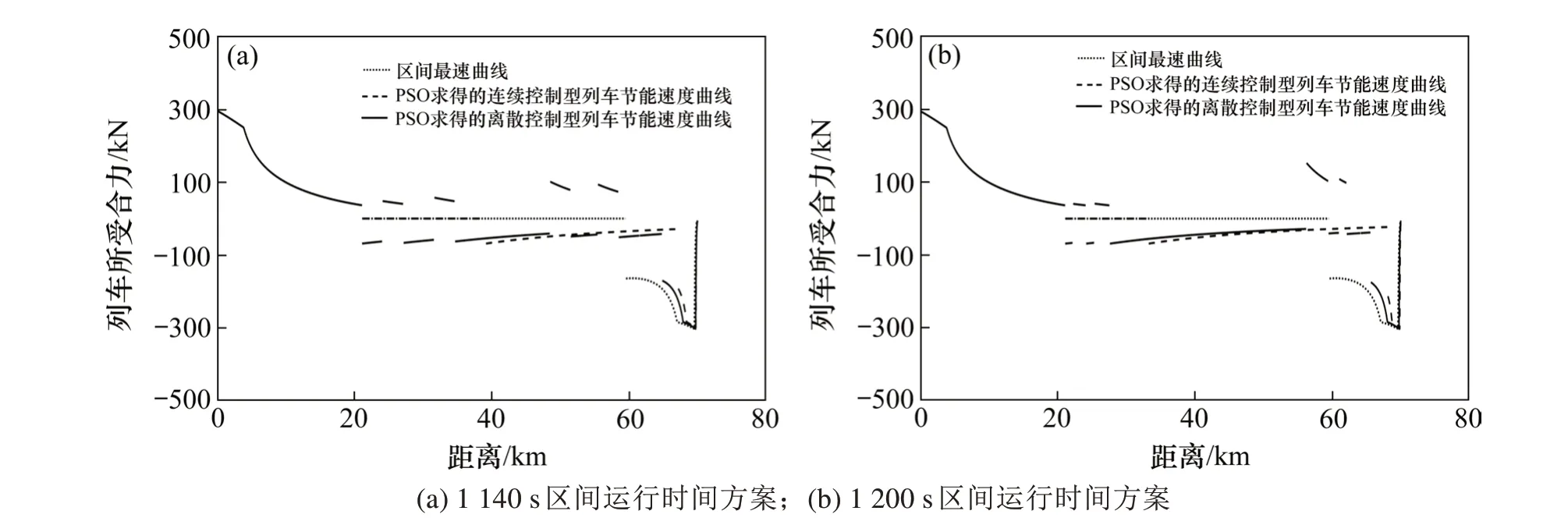
图8 图7中列车速度曲线的列车所受合力变化情况Fig.8 Variation of the combined force on the train for the train speed profiles in Fig.7

在3.2节连续控制型列车节能驾驶策略优化和3.3节离散控制型列车节能驾驶策略优化中，PSO优化取得了更优的优化效果，因此采用PSO求解列车在水平线路上的2种节能驾驶策略。

分析表5，同样可以发现1 200 s区间运行时间方案的列车节能速度曲线运行能耗均低于1 140 s区间运行时间方案的列车节能速度曲线。对比分析2种速度控制模式，发现离散控制型列车节能速度曲线的能耗更低；考虑线路条件和再生制动技术，其原因在于水平线路上CR运行工况需要一直施加部分牵引力以克服列车基本阻力，而MA-CO运行工况对可以部分减少列车在CR运行工况的牵引能耗。此外，在相同的区间运行时间和速度控制模式下，表3和表4中PSO求得的列车节能速度曲线运行能耗均低于表5中PSO求得的列车节能速度曲线，这说明线路中的下坡道在优化算法的作用下对列车驾驶策略的节能优化具有促进作用。

表5 水平线路上3种列车速度曲线的性能指标Table 5 Performance indicators for three train speed profilesof the train running on the level track

4 结论

1)适当延长列车区间运行时间可以有效降低列车区间运行能耗，且列车区间运行时间越长则列车区间运行能耗越低。

2)连续控制型列车节能速度曲线和离散控制型列车节能速度曲线均能有效降低列车区间运行能耗。在含有下坡道的变坡度线路上，由于PB运行工况和再生制动能量反馈，连续控制型列车节能速度曲线的节能效果优于离散控制型列车节能速度曲线；在水平线路上，通过MA-CO运行工况对的组合替换长距离的CR运行工况，离散控制型列车节能速度曲线的节能效果优于连续控制型列车节能速度曲线。

3)2种速度控制模式的列车驾驶策略多目标优化过程中，PSO的节能优化效果均优于SA和PS。

4)坡道附加阻力对列车运行过程的影响显著，体现在列车速度曲线及其对应的列车所受合力的变化上；此外，下坡道在优化算法的寻优作用下对列车驾驶策略节能优化具有促进作用。

5)本文提出的列车驾驶策略多目标优化方法不仅适用于高速列车，也适用于普速列车、城轨列车和重载列车，只需调整对应的列车动力学参数，并设置合适的列车运行工况切换序列。