考虑城市轨道交通折返进路占用的大小交路列车运行组织优化

谭彬彬，金华，刘爽，陈绍宽

(1.北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；2.北京交通大学 中国综合交通研究中心，北京 100044)

目前，关于城市轨道交通列车运行组织优化模型的研究通常借助最小折返时间代替折返进路组织的安排[1-2]，列车在折返站内的作业过程犹如一个“黑箱”。随着线路高峰小时断面客流的持续增加，发车间隔不断压缩至最小，在传统列车运行图编制的过程中考虑折返进路的占用，可以进一步压缩折返间隔，提高折返效率。大小交路运营模式由于列车折返作业办理频繁，考虑折返进路排列对提高线路通过能力更具意义[3]。国内外关于列车运行组织优化的研究主要集中在时变客流需求下的非周期列车运行图，但模型中关于列车折返接续、车底运用的约束设置得较为简单[4-6]。姚宇等[1,7-9]针对列车折返接续过程仅考虑了折返时间的限制和车次间的接续匹配。关于折返间隔计算的文献较多，但多数学者是通过典型的数学归纳法、图解法进行实例分析和评估，提出提高折返效率的可实施措施。王俊锋[10]对典型站后折返站的单线折返和双线交替折返方式进行了详细的折返间隔计算；徐意[11]推导了列车折返时间与折返间隔之间的相互关系；王潇骁等[12]分析了影响站后双折返线折返站折返能力的关键因素；陈垚等[13]以站后双折返线折返站为例，阐述了接车进路的安全区段不同延伸长度情况下的单线折返过程。仅有少数文献对折返组织过程进行数学建模，且通常是在给定列车到发时刻的前提下进行研究，如JIANG等[14-15]基于N-track理论构建相关模型。折返站能力计算通常独立分析，未考虑列车时刻表与折返间隔的相互影响。鉴于此，本文在不考虑客流因素的前提下，对典型站前、站后折返站型的折返过程进行建模，在此基础上构建了运营高峰时期考虑折返进路占用的大小交路列车运行组织优化模型。

1 问题描述

考虑有N个车站且具备开行大小交路列车条件的城市轨道交通线路，如图1所示。车站n是中间折返站，车站1及车站n后方通过出入段线相连车辆段。在站1和站N之间开行大交路，在站N和站n之间开行小交路，不考虑嵌套交路等情况。

图1 大小交路模式下的城市轨道交通线路示意图Fig.1 Urban rail transit line under the full-length and short-turn routingmode

研究问题可描述为：在已知大小交路形式和发车比例的前提下，考虑不同折返方式，通过调整列车在各站点的到发时刻以及对折返站轨道资源的占用情况进行运行图通过能力的优化。模型假设线路所属车底数量有限、技术参数相同且车辆段能力充足。此外由于中间普通站的到发时刻不影响通过能力，为简化求解，仅考虑折返站的到发时间，普通站的停站时间与站间运行时间约束将整合为折返站间的区间运行时间约束。

后续建模涉及的符号定义如表1所示。表中仅列出上行车次相关的符号，下行车次符号与上行类似。

表1 参数、变量定义Tab le 1 Definition of parametersand variables

2 基于累积0-1变量的折返组织建模

依据TÖRNQUIST等[16]提出的N-track理论，对较为典型的站前交叉渡线折返站和站后双折返线折返站进行建模，区域划分如图2和图3所示，其中交叉渡线与折返线视为双向通行的轨道，其余轨道单向通行，通行方向如图中箭头标记所示。对所有轨道依次标号，渡线区域的轨道记为折 返 线 区 域 的 轨 道 记 为则 站 前“直进侧出”折返方式的折返路径为：，“侧 进 直 出”的 折 返 路 径 为：。站后折返路径以此类推。

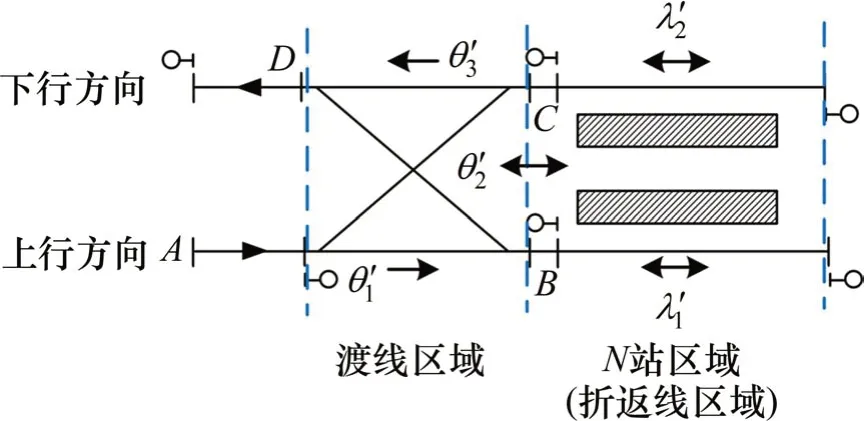
图2 典型站前交叉渡线折返站区域划分Fig.2 A rea division for typical station w ith crossovers located in frontof the platform

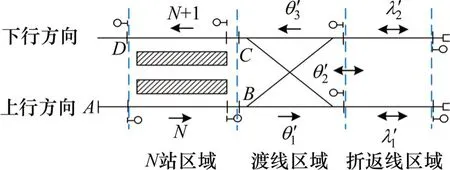
图3 典型站后双折返线折返站区域划分Fig.3 A rea division for typical station w ith crossovers located behind the platform

折返组织建模主要需要解决折返轨道占用相容性约束以及折返路径选择约束。前者保证轨道占用不产生冲突，后者保证每个车次选择一条折返路径，且该路径的占用符合作业要求。

2.1 折返轨道占用相容性约束

根据折返组织过程，任意时刻，每条折返线及整个渡线区域只能被一列列车占用。据此可以分别定义折返线占用相容性约束和渡线区域轨道占用相容性约束。为方便表达这两类约束，本文假设：当某上行车次iup与某下行车次idown在折返站N的某一折返线λN上接续时，整个折返过程都视为上行车次走行的一部分，记录到上行车次的时刻表中。下行方向类似。

采用累积0-1变量表示车次i到达和离开折返线轨道λ的时刻，首先要对时间进行离散化，再引入变量ai,λ,t和di,λ,t分别表示车次i在t时刻是否已经到达和离开折返线轨道λ。借助变量ai,λ,t，di,λ,t和中间变量yi,λ,t即可表示车次i对轨道λ的时间占用，如图4所示。中间变量yi,λ,t表示车次i在t时刻是否占用λ。yi,λ,t与ai,λ,t，di,λ,t之间的计算关系如式(1)所列。

图4 车次对折返线轨道资源的占用时长示意图Fig.4 Illustration of train’soccupation duration of turn-back track

车次i到达和离开轨道λ的时刻ai,λ，di,λ可以由ai,λ,t，di,λ,t计算得到，如式(2)和式(3)所列。式中，T表示运行图编制的总时间，acc表示时刻t的离散粒度。故轨道占用相容性约束可表达如式(4)所列。

2.2 折返路径选择约束

对于每个折返站一般都有2种折返路径，用和分别表示车次i是否采用这2种路径。式(5)保证了每个车次只选择一条折返路径，其中I为所有车次集合。

此外对每种折返路径需单独根据折返作业确定其路径上轨道的占用时间。以站前折返方式下的“直进侧出”折返路径为例，列车在各轨道资源的到发时刻之间存在由列车占用折返进路作业决定的推算关系。令折返站的到发时刻为aiup,N,didown,N+1，据此可获得列车占用折返线及渡线区域轨道的时间如图5所示，其中和分别是列车在进折和出折方向渡线区域轨道的最小作业时间。据此可依次得到该折返路径对的占用时间约束如下，其中iup为上行方向车次，下行方向类似。

图5 站前折返方式下列车折返进路时空占用Fig.5 Space-time occupancy of train’s turn-back route under the ahead-station turn-backmode

1)进折方向渡线区域轨道：

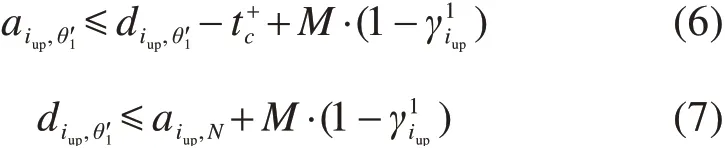
式(6)保证了进折作业时间；式(7)保证车次要在离开进折方向渡线区域轨道再进入折返线。

2)折返线区域轨道：

式(8)和式(9)保证了折返线区域轨道占用时间要包含折返站的到发；式(10)保证了折返线的作业时间。

3)出折方向渡线区域轨道：

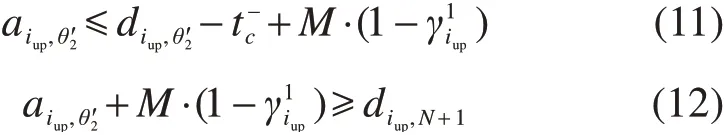
式(11)保证了出折作业时间；式(12)保证车次要在先离开折返线区域再进入出折方向渡线区域轨道。

3 大小交路列车运行组织优化模型建立

3.1 目标函数

从运营角度出发，模型的目标设置为最小化列车运行图的周期时间，如式(13)所列，等价于最大化线路通过能力。式中aLdown,2N是一个完整周期内下行末班车次到达终点站的时刻，d1up,1是上行首班车次离开起点站的时刻。

3.2 约束条件

模型主要考虑列车运行、折返接续相关约束以及额外的一些约束。为简化表达，仅列出上行车次的各类约束，下行车次以此类推：

1)首班车运营时间约束。上、下行各交路的首班车次在起点站的发车时刻须确保在一个合理的范围内变化。

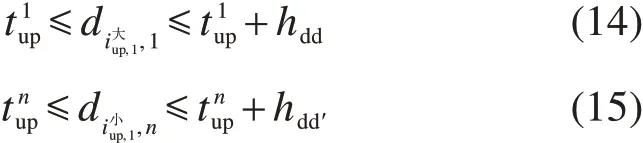
2)停站时间约束。由于列车在起终点站的停站时间包含在折返过程中，这里仅考虑大交路列车在中间折返站的停站时间。

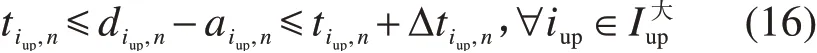
3)区间运行时间约束。考虑折返站间列车运行时间的范围限制。

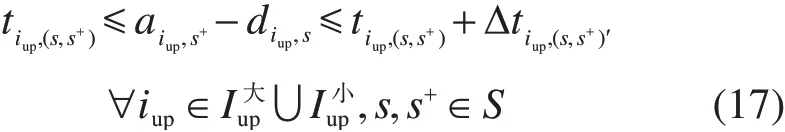
4)行车间隔约束。各行车方向上车次间到达、离开同一站台的时刻需要大于等于最小间隔。

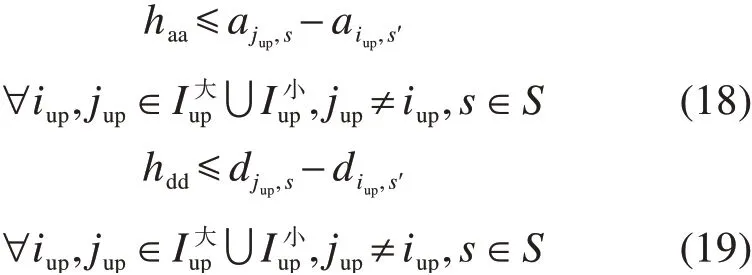
另外，对于中间折返站，若是站前折返站型，小交路列车在折返过程中会占用正线，如图6所示，则还需加入折返列车与通过列车的发到间隔约束。

图6 中间折返站列车行车间隔示意图Fig.6 Illustration of trains'headway at intermediate turn-back station

5)接续唯一性约束。上、下行车次间的接续必须满足唯一性要求。具体来讲，对于折返站N，任意上行车次结束运营后必须与下行某一车次在某一条折返线上实现接续。这类约束是严格约束，即式(21)和式(22)左项等于1。

对于折返站1和n，由于连接车辆段，允许不被接续的车次，这类约束是宽松约束，上式左项小于等于1。

6)折返时间约束。当2个行车方向的车次接续时，列车的折返时间需要满足折返时间的范围限制，具体的折返时间取值视折返站站型而定。

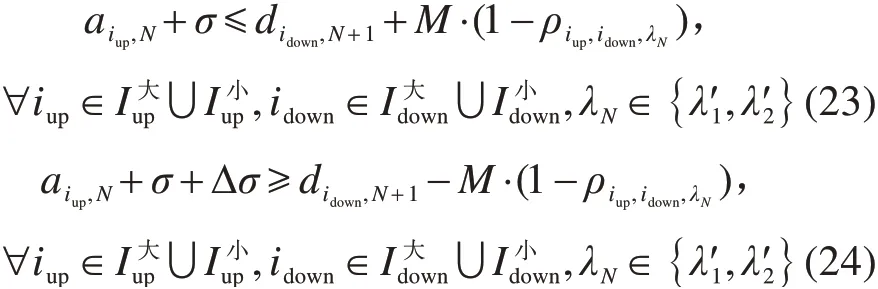
7)轨道占用相容性约束与占用开始和结束时间约束，详见第2节。

8)累积0-1变量连续性约束。由累积0-1变量本身的性质所决定，0-1序列后一时刻的取值大于等于前一时刻的取值，式中x是折返站任意折返线、渡线区域轨道的索引。

9)车底数量限制约束。由于线路所属的车底数量有限，承担车次任务的车底数量必须小于等于最大车底数。

综上所述，考虑折返进路占用的大小交路列车运行图优化模型构建完毕。

4 案例分析

4.1 参数设置

以虚拟线路数据为基础进行算例验证。模型涉及的列车运行、折返相关参数见表2和表3。其中σ为参考经典折返间隔计算方法[10-11]得到的最小折返间隔，用作对比分析。模型借助Gurobi求解器进行求解。

表2 模型基本参数取值Table 2 Basic parameters for themodel

表3 折返站基本参数取值Tab le 3 Basic parameters for the turn-back stations

4.2 考虑折返进路占用的效果分析

构建2种线路折返站布置形式：方案1设折返站N为站后双折返线折返站，折返站1和折返站n为站后单折返线折返站；方案2设折返站N为站后双折返线折返站，折返站n为站前单渡线折返站，折返站1为站后单折返线折返站。在大、小交路发车比例为1∶1的情况下进行案例分析，其中本文优化模型求得结果作为实验组，传统基于折返间隔计算公式[7-8]推算的大小交路列车运行图作为对照组。

方案1结果如表4所列，采用本文优化模型的实验组结果中的运行图周期时间较小，线路通过能力较大，且最小发车间隔相较对照组降低了15 s，这说明通过对折返进路具体占用的考虑可以充分挖掘折返能力，提高运行图效率。

表4 方案1结果对比Table 4 Results comparison of case 1

方案2结果如表5所列，当中间折返站为站前折返站时，实验组运行图可以压缩小交路的发车间隔至145 s，相比对照组降低了30 s，线路通过能力每小时提高了4对，同样提高了运行图效率。需要说明的是方案2和方案1的实验组均调整了车次接续，从而增加了部分车底，但未违反线路配属最大车底数的限制。此外，对比方案1和方案2可以发现，中间折返站形式对开行大小交路列车的线路通过能力影响显著：中间站为站前单渡线折返站的方案2的线路通过能力相较于中间站为站后双折返线折返站的方案1，降低了33.3%。

表5 方案2结果对比Tab le 5 Results comparison of case 2

5 结论

1)基于累积0-1变量对典型站前折返站型和站后折返站型进行了折返组织过程的数学建模。然后在此基础上，从运营角度出发最大化线路通过能力，着重优化列车折返进路的排列，建立了大小交路运营模式下的考虑折返进路占用的列车运行组织优化模型。

2)案例分析着重对考虑进路占用的优化模型与基于最小折返间隔的传统模型进行对比，结果表明优化模型求得的列车运行图具有较高的折返效率，验证了考虑折返进路占用可进一步压缩列车折返间隔，提高线路的整体通过能力。

3)考虑到加入折返进路排列的列车运行组织优化模型整体的复杂性，本文对模型进行了简化。该模型未考虑时变客流，未来可以尝试引入时变断面客流对发车间隔进行同步优化，同时目标函数也可以从乘客的角度进行设置。