运用相位差解决机械波中的疑难问题

周国庆

(江苏省金坛区第一中学 213200)

人教版选择性必修第一册P37，“做简谐运动的物体处于一个周期中的哪个状态叫相位；两个频率相同的简谐运动相位之差叫相位差.当φ1>φ2时，Δφ=φ1-φ2此时，我们说1的相位比2超前Δφ，或2的相位比1滞后Δφ”.笔者认为这种超前或滞后本质上体现的是质点振动过程中的“时空性”，即质点振动时间的先后或质点平衡位置距波源的前后(远近).以下是笔者分别从时间和空间两个维度对相位差(Δφ)和它们的关系进行的归纳.

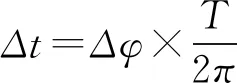
例1(2021·甲卷)均匀介质中质点A、B的平衡位置位于x轴上，坐标分别为0和xB=16cm.某简谐横波沿x轴正方向传播，波速为v=20cm/s，波长大于20cm，振幅为y=1cm，且传播时无衰减.t=0时刻A、B偏离平衡位置的位移大小相等、方向相同，运动方向相反，此后每隔Δt=0.6s两者偏离平衡位置的位移大小相等、方向相同.已知在t1时刻(t1>0)，质点A位于波峰.求：

(1)从t1时刻开始，质点B最少要经过多长时间位于波峰；

(2)t1时刻质点B偏离平衡位置的位移.

解(1)t1时刻(t1>0)，质点A位于波峰，波形沿x轴正方向传播，该波形传播到B经历的时间：

则质点B最少要经历0.8s时间位于波峰；

(2)t=0时刻A、B偏离平衡位置的位移大小相等、方向相同，运动方向相反，此后每隔Δt=0.6s两者偏离平衡位置的位移大小相等、方向相同.因为每经过半个周期质点运动到与该点对称的位置，所以可得出：

波长：λ=vT=20×1.2cm=24cm

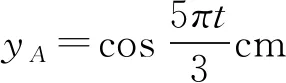
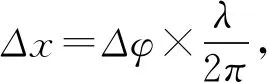
B滞后A振动，所以B的振动方程：

在t1时刻(t1>0)，质点A位于波峰,即yA=1cm, 不难求得此时yB= -0.5cm

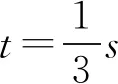
图1

解略

例3甲、乙为一列沿x轴方向传播的简谐横波上的两个质点，两质点平衡位置的间距为x=3m，图2中的实线和虚线分别为质点乙和质点甲的振动图像.如果波由质点甲向质点乙传播，求该波的传播速度.

图2

解由图像可得，两质点的振幅均为A=2 cm，周期为T=0.4 s

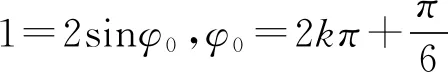
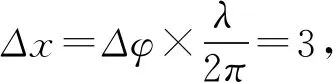
例4如图3所示，图3(a)为一列沿x轴传播的简谐横波在某时刻的波形图，P为平衡位置在x=17.5cm的质点，图3(b)为此波中平衡位置坐标x=10cm的质点从该时刻起的振动图象，求从该时刻起，P点第一次回到平衡位置通过的路程.

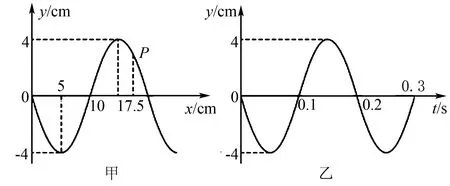
图3

解由图3(a)、图3(b)两图知λ=20cm,T=0.2s得V=1m/s.由图3(b)还可判断x=10cm的质点该时刻振动方向向下，因此波以1m/s沿x轴正方向传播.

设x=15cm处的质点为Q点，此时振动方程：

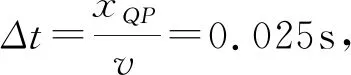
要注意的是，用相位差解决问题时，初相位的确定是关键，很多学生会忽视初相位与质点振动方向的关系而造成错解，下面以2016年天津高考第7题为例.

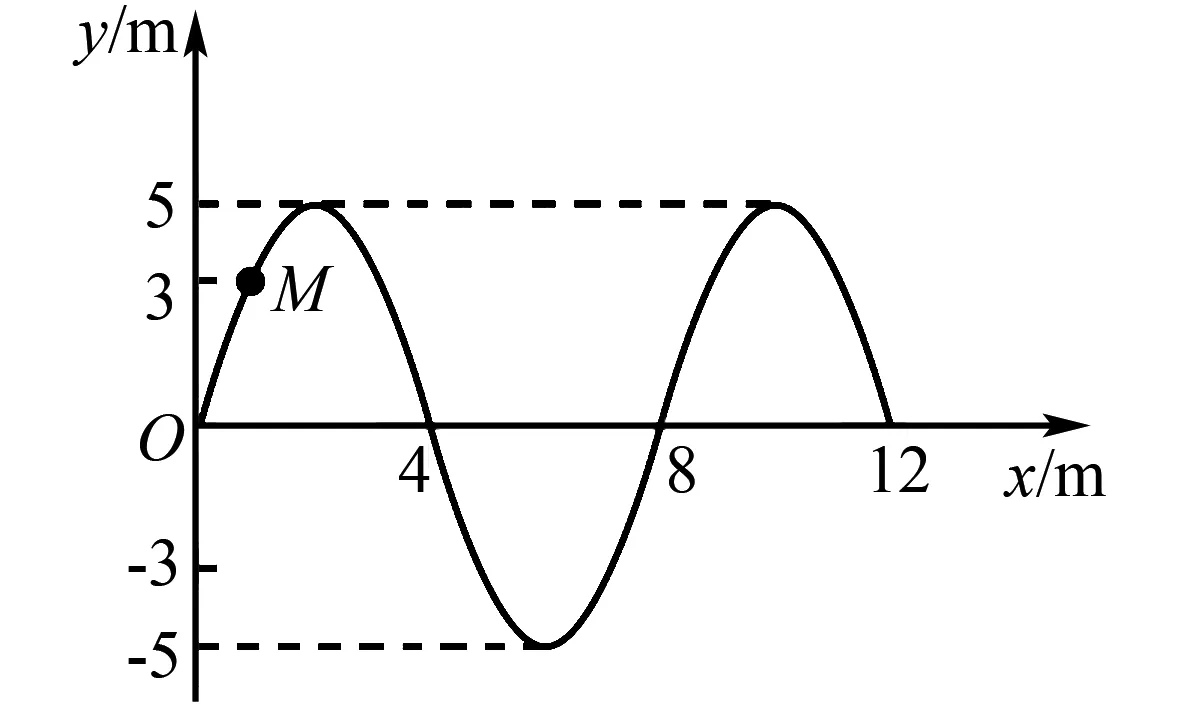
图4

A．此后再经6 s该波传播到x=24 m处

B．M点在此后第3 s末的振动方向沿y轴正方向

C．波源开始振动时的运动方向沿y轴负方向

D．此后M点第一次到达y=-3 m处所需时间是2 s

对于A、B、C选项这里不再重复，较易得到AB正确.对于D选项，以下是笔者列出学生错解过程供参考.

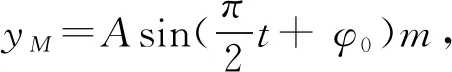
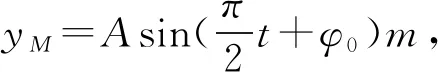
当机械波中质点某时刻处于波峰、波谷或平衡位置时，这类型题学生撑握起来比较容易，但质点不处于上述位置时，运用“相位差”求解这类疑难问题是一种符合学生认知的好方法.通过课堂教学实践，绝大部分学生能很快理解并应用，以上是笔者教学中的一点体会.