近五年高考数学文化命题的特点与启示

巨小鹏

(陕西省汉中市龙岗学校 723102)

顾沛教授说数学文化包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系以及数学与各种文化的关系等.新课标中多次指出要将数学文化融入课程内容、融入数学教学活动中和渗透在日常教学中，体现出时代性，特别是如何将数学史和数学美融入数学课堂教学是数学教育领域的一个重要课题，通过让学生了解数学概念的发生过程和思想方法的形成过程，一方面可以使学生感受丰富多彩的数学文化底蕴，做好文化传承，激发数学学习的兴趣，另一方面也有助于学生对数学概念本质的理解和其思想方法的掌握.

1 数学文化命题统计以及特点分析

1.1 近五年数学文化命题统计

表1 2017-2021年高考卷中数学文化命题特点统计

1.2 数学文化命题特点分析

从以上统计我们可以看到：(1)数学文化背景题理科考查比文科多.全国卷基本每年都有涉及，已经成为常态，通过对比，每年题量相当；(2)可以看出题型以选择填空题呈现，并且以中国古代文化瑰宝文献摘取居多，国外文化艺术也有涉及，比例不大.全国卷以外的浙江卷除了2020年每年都会涉及数学文化题，都是关于中国古代文化；(3)从考查知识点内容可以看出有解三角形、几何体体积、图形面积、数列以及求和、几何概型、古典概型、曲线与方程以及不等式等；(4)数学文化为背景的考查最终落脚点还是数学基础知识的考查，由于阅读量较大和语境陌生等原因，题的难度才会加大，只有在平时加强阅读量，才能够很快进入题意语境，理解题意，分析题意，然后通过学过的数学工具去解决问题.

2 命题趋势与经典例题赏析

2.1 以中国文化瑰宝为背景

我国历史源远流长，灿烂文化更是民族的骄傲，由于语言的障碍，今天的我们对老祖宗留下的财富知之甚少，对其研究者更是寥寥无几.尽管古代研究没有像西方那样形成研究风尚，让更多的国人通晓其精妙之理，但我们的研究功不可没，造诣更是非凡，比如《数书九章》《周易》《数术记遗》《四元玉鉴》《算经十部》等很多成果领先其他国家很多年之久.借助今日体系之研究，理解古人博大的文化底蕴，增强民族自豪感，以此激励更多的人在学术无国界的知识海洋里探索、追求寻找更加奇妙的万物之规律，为人类造福祉，为求真理孜孜不倦.

图1

故选B.

评注《九章算术》是《算经十部》中最重要的一部，总结了战国秦汉时期的数学成就，最早提到分数问题、盈不足问题、负数和加减运算法则问题等，分别囊括“方田”(平面几何图形面积计算包括长方形、三角形、直角梯形、等腰梯形、圆形、扇形、弓形和圆环以及分数四则运算)、“粟米”(谷物粮食比例折换和比例分配法则)、“衰分”(比例分配问题)、“少广”(已知面积和体积求边长、开平方和开立方)、“商功”(土石工程、体积计算和工程分配方法)、“均输”(正反比例、比例分配、复比例和连锁比例等)、“盈不足”(双设法问题、盈不足、盈适足和不足适足、两盈和两不足等问题)、“方程”(一次方程组、分离系数表示线性方程组即矩阵、矩阵初等变换、负数、正负数加减法则和正负数乘除法)、“勾股”(勾股数问题)等九个方面.

例2(2021届西安中学模拟)《数术记遗》是《算经十书》中的一部，相传是汉末徐岳(约公元2世纪)所著，该书主要记述了：积算(即筹算)太乙、两仪、三才、五行、八卦、九宫、运筹、了知、成数、把头、龟算、珠算计数14种计算器械的使用方法.某研究性学习小组3人分工搜集整理14种计算器械的相关资料，其中一人4种、另两人每人5种计算器械，则不同的分配方法有( ).

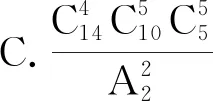
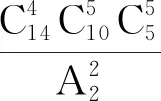
评注此题主要考查排列组合计算，考查平均分组是需要注意的地方，考查本身与书中算法没有关系，从表面形式让学生了解古代文化经典的大概内容.

2.2 以外国数学文化为背景

柏拉图说，打开宇宙之谜的钥匙是数学和几何图形.外国数学发展以追求理性为动力，特别是早期古希腊哲学家以毕达哥拉斯最为出名，开始了研究数学的传统，还有亚里士多德对于理论科学特别是数学的研究，被他称为形而上学的第一哲学，学问之起点.当然还有泰勒斯、欧几里得、阿基米德、高斯、牛顿、笛卡尔、柯西和泰勒等数学家的研究，让数学的皇冠耀眼辉煌，充满真理光辉，照耀着万物生灵，启迪着未来智慧.

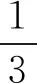
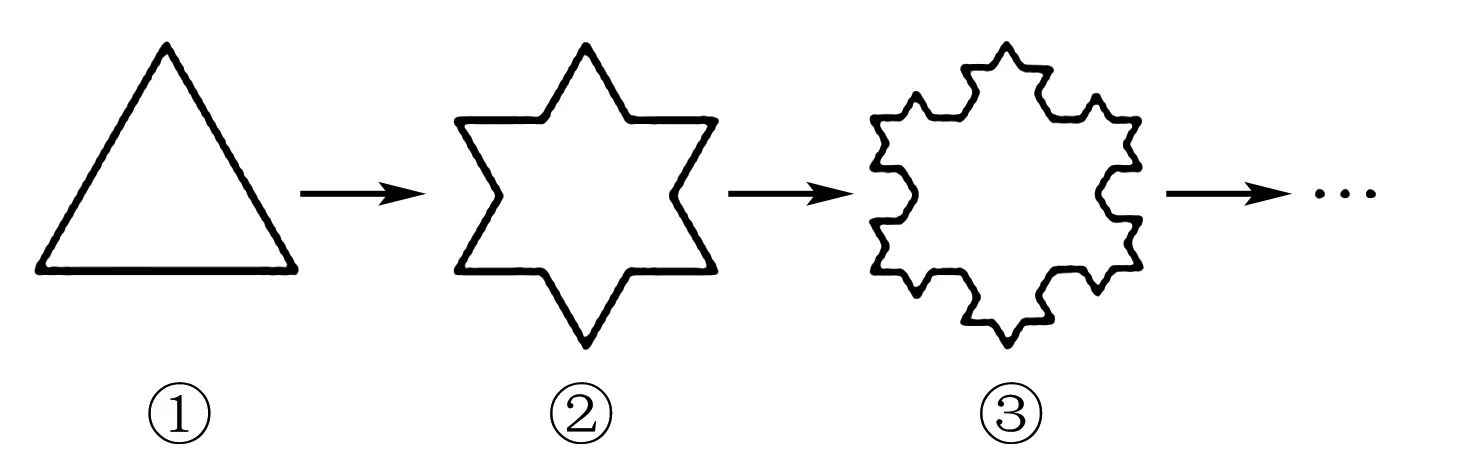
图2

B．记第n个图形的边数为an，则an+1=4an；

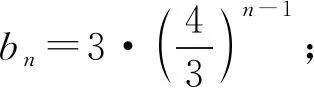
D．记第n个图形的面积为Sn，则对任意的n∈N+，存在正实数M，使得Sn

由各个图形的边数也成等比数列且q=4，所以an=3·4n-1，所以B正确；

当n→∞时，图形无限接近于圆，可得Sn

故选BCD.

评注“燕山雪花大如席，片片吹落轩辕台”，北京奥运会的火炬在一朵巨大的雪花中闪烁升腾，张艺谋用“一朵雪花的故事”讲述国人奥运精神，科赫探寻雪花的奥秘后提出了著名的“雪花”曲线.

例4(2021届衡水中学模拟)卡西尼卵形线是1675年卡西尼在研究土星及其卫星的运行规律时发现的．在数学史上，同一平面内到两个定点(叫做焦点)的距离之积为常数的点的轨迹称为卡西尼卵形线．已知卡西尼卵形线是中心对称图形且有唯一的对称中心．若某卡西尼卵形线C两焦点间的距离为2，且C上的点到两焦点的距离之积为1，则C上的点到其对称中心距离的最大值为( ).

解析设左、右焦点F1，F2的中点为坐标原点，F1,F2所在的直线为x轴建立平面直角坐标系，则F1(-1,0),F2(1,0)．

设曲线上任意一点P(x,y)，则

化简得该卡西尼卵形线的方程为(x2+y2)2=2(x2-y2)，显然其对称中心为(0,0)．

故(x2+y2)2=2(x2-y2)=-4y2≤0.

所以(x2+y2)2≤2(x2-y2).

所以0≤x2+y2≤2.

故选B.

评注卡西尼卵形线是天文学家乔凡尼·卡西尼对卵形线的研究结果，他还是第一个发现土星的四个卫星的人，发现了土星光环间的暗缝即卡西尼缝，有个以他命名的土星探测器“卡尼西号”.

2.3 以科技成果和生活日常为背景

日新月异的今天，现代科技的发展使得数学发展显得尤为重要.怀特说工匠后面是化学家，化学家后面是物理学家，物理学家后面是数学家.数学是一切科学的起点，数学也造就了今日科技发展，借助新的科技成果，让学生走近科学和了解科学，解开科技神秘面纱，让学生知道平时所学即是现代科技的基础，从而坦步走进科学殿堂，追寻真理智慧之光.

例51970年4月24日，我国发射了自己的第一颗人造地球卫星“东方红一号”，从此我国开启了人造卫星的新篇章，人造地球卫星绕地球运行遵循开普勒行星运动定律：卫星在以地球为焦点的椭圆轨道上绕地球运行时，其运行速度是变化的，速度的变化服从面积守恒规律，即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.如图3，设椭圆的长轴长、焦距分别为2a，2c，下列结论不正确的是( ).

图3

A．卫星向径的最小值为a-c

B．卫星向径的最大值为a+c

C．卫星向径的最小值与最大值的比值越小，椭圆轨道越扁

D．卫星运行速度在近地点时最小，在远地点时最大

解析根据题意，向径为卫星与地球的连线，即椭圆上的点与焦点连线的距离.根据椭圆的几何性质有：卫星向径的最小值为a-c，卫星向径的最大值为a+c，所以A,B正确.

卫星运行速度在近地点时,其向径最小，由卫星的向径在相同的时间内扫过的面积相等，则卫星运行速度在近地点时最大，同理在远地点时最小，所以D不正确.

例6(2022届合肥市联考)如图4，奥运五环由5个奥林匹克环套接组成，环从左到右互相套接，上面是蓝、黑、红环，下面是黄，绿环，整个造形为一个底部小的规则梯形．为迎接北京冬奥会召开，某机构定制一批奥运五环旗，已知该五环旗的5个奥林匹克环的内圈半径为1，外圈半径为1.2，相邻圆环圆心水平距离为2.6，两排圆环圆心垂直距离为1.1，则相邻两个相交的圆的圆心之间的距离为( ).

图4

解析如图5所示，由题意可知|AB|=2.6.

图5

在△ABC中，取AB的中点D，连接CD，所以|BD|=1.3，|CD|=1.1.

又因为AC=BC，所以AB⊥CD.

除了以上介绍的数学文化命题，还有很多，比如南宋杨辉的《日用算法》中有度量衡换算、土地丈量、仓窖容积、建筑工程、商品交换以及日常生活中与数学有关的问题，《杨辉算法》中记录了世界上第一个排列纵横图(即幻方)，并且从中总结出构成规律的理论知识，改进乘除计算算法；垛积术即高级等差数列的研究以及等差数列求和公式；杨辉三角(准确说是贾宪三角)是二项式系数在三角形中的几何排列.我国古代乐理、围棋、中药和建筑等方面都有很深的造诣.外国数学文化题也有很多，比如欧拉线、斐波那契数列和高斯函数等.教学过程中应该关注数学与生活的紧密联系，关注时政与数学的应用，关注数学与科技的融合，更应该关注新教材和新课标下的数学文化渗透和教学，重视课本阅读材料和例题应用，以此内化数学核心素养，落实立德树人的任务.