基于母线电流采样的开关磁阻电机自抗扰控制
2022-09-22侯利民杨玉岗
郭 词,侯利民,王 巍,杨玉岗
(1.辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105;2.太原理工大学 电气与动力工程学院,山西 太原 030024)
0 引言
开关磁阻电机(switched reluctance motor,SRM)由于其结构简单、机械强度高、成本低、控制灵活、容错能力强、无需永磁材料等优点,吸引了国内外学者的广泛关注,目前已广泛应用于油田开采、地下矿井传动、电动汽车、小家电、纺织等领域.
由于开关磁阻电机在运行过程中需要对各相绕组电流进行采样,作为电流控制器的输入,用以控制电机转矩.因此获得准确且时效性高的电流信号,对于抑制电机的转矩脉动和提升系统调速性能至关重要.传统的开关磁阻电机控制系统中,通常需要根据电机相数安装多个电流传感器,以便实时获取各相电流值为电流环控制器提供反馈信息.由于开关磁阻电机的驱动电路拓扑多采用不对称半桥电路,这种拓扑结构下驱动电路的直流母线中,包含着电机运行所需要的全部电流信息.所以,本文通过仅在驱动电路直流母线上安装一个电流传感器,将母线电流信息依据不同驱动模式进行分类处理,得到可供于控制器使用的电流信号实现闭环控制.
母线电流采样技术,作为一种可以有效简化接线结构、降低系统总体成本的方法,已经在各类电机上进行了初步探索和应用[1-3].开关磁阻电机由于其各相电气回路相对独立的特性,比较适用于母线电流采样技术,所以很早就被国外学者发现[4],但国内相关研究热度相对较低.文献[5]提出一种运用高频脉冲注入的方法,从母线中提取相电流信息的方案.该方案虽然解决了开关磁阻电机相电流重构的难题,但存在需要预留出一定占空比以供脉冲注入的缺点,时间窗口利用率降低,驱动器功率不能满载.文献[6]提出一种基于H桥驱动电路的单电阻采样的电流检测方案,通过改造接线结构测量出相绕组电流和续流二极管电流之和的方法,实现相电流的重构,但存在非观测区电流突起和适用电机结构受限等问题.
本文提出一种单电流传感器母线电流采样法,并给出了母线采样电流作为直接反馈的依据.针对双相启动、直接瞬时转矩控制(direct instantaneous torque control,DITC)等存在相电流重叠问题的驱动方法,给出一种基于改进型转矩分配函数法(torque sharing function,TSF)的解决方案.不同于传统的相电流重构法,该方案提出了一种在转矩层面上解决相电流重叠和转矩脉动难题的新思路.
为解决开关磁阻电机转矩脉动较大的问题,使用滑模控制[7]、模糊控制[8]、神经网络[9]等先进控制算法,用于抑制转矩脉动.自抗扰(active disturbance rejection controller,ADRC)技术中的“总扰动”概念,在抑制开关磁阻电机转矩脉动方面有着更容易理解的物理解释.不依赖电机精确模型的设计方法,使其在实际应用中具有很强的可操控性.文献[10]使用自抗扰控制技术实现转速闭环控制,文献[11]、文献[12]将模糊控制、迭代学习等先进算法与自抗扰技术相结合为解决转矩脉动问题提供了新思路.
本文采用单电流传感器采样母线电流作为输入,结合自抗扰控制技术实现对外部扰动转矩和自身转矩脉动的有效抑制,最后通过仿真和实验验证控制策略的有效性.
1 不对称半桥母线电流分析
1.1 相电流无重叠时母线电流分析
常用SRM 驱动电路由电机相数个单相不对称半桥电路并联而成,由于各相驱动电路的独立性且各相互感效应很小可忽略不计,通常仅需要分析其中一相即可,单相不对称半桥运行状态见图1,不对称半桥电路由一对 MOSFET管和一对续流二极管组成.通常情况下将变换器设定为软斩波模式,即:将一个开关管根据相位角开断,另一个接受速度控制器斩波.这种模式降低了器件的开关损耗,有利于低速时转矩脉动的抑制.但缺点是输出转矩不足,启动转矩低.而硬斩波驱动模式更适合使用母线电流采样法.
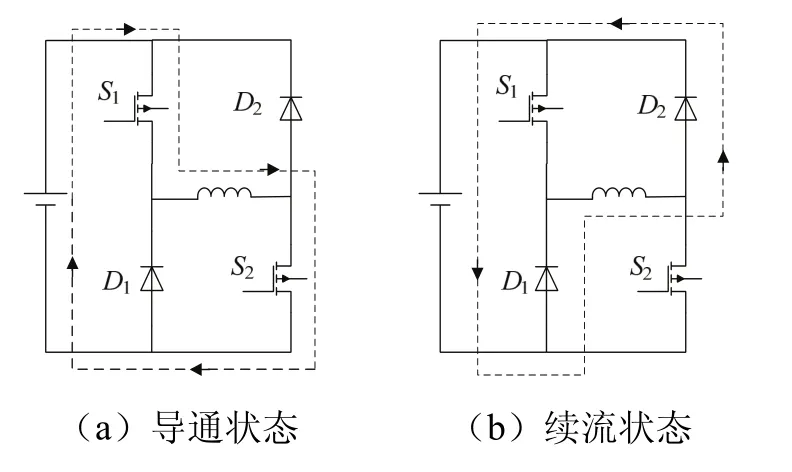
图1 单相不对称半桥运行状态Fig.1 single-phase asymmetric half-bridge operating state
图1中硬斩波导通方式,具体运行模式为:当电机角度到达开通位置时,所对应的开关管S1、S2同时开通;当相电流超过最高电流限值,S1、S2同时关断,同时对角的两个二极管间进行续流;当相电流跌落到最低电流限值时,再次开通S1、S2管,相电流上下往复变化.当位置角度大于关断角后,S1、S2关断,绕组电流通过对角的续流二极管回馈电源.
值得注意的是,在电机低转速或轻负载运行时,单步换相硬斩波驱动方式可以令各相电流没有励磁重叠,仅有少量传导重叠甚至无重叠,这使得母线电流idc基本等于导通区间的励磁电流为

由图1和图2可知,在单步换相硬斩波运行模式下,仅需要装设一个母线电流传感器,并采用A/D采样通道进行采样,再通过单片机或DSP的采样序列通道,依次赋给各相电流环控制器,就可替换图2所示的传统接线方法,实现相同控制效果.图3中LEM代表所用相霍尔电流传感器.
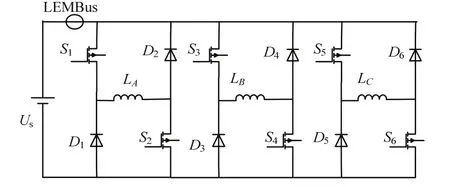
图2 单电流传感器接线Fig.2 single current sensor wiring
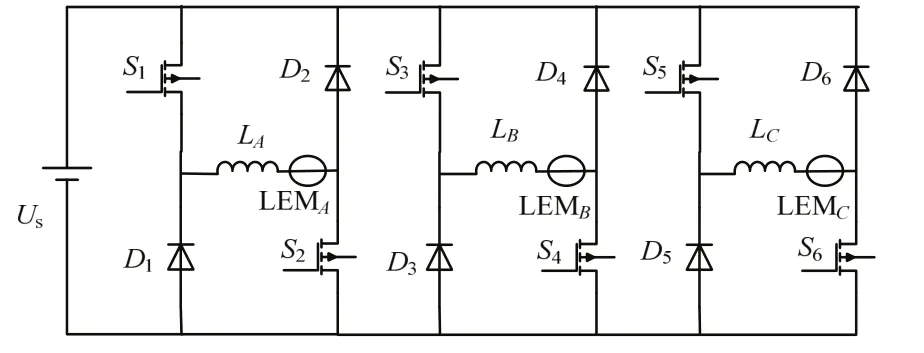
图3 多相电流传感器接线Fig.3 multiphase current sensor wiring
1.2 相电流重叠时母线电流分析
当使用双相启动、直接瞬时转矩控制等方式驱动开关磁阻电机时,将会发生两相同时导通的情况,进而产生励磁电流重叠现象.为避免此类问题,故本文给出一种适用的母线电流矫正方式.首先根据导通相数量区分出单相导通模式和双相导通模式.
仅有单相导通的情况见图4,其交叠电流来自于其他导通相的传导交叠电流,而由于开关磁阻电机电流回路独立的特性,其互感电流非常小,可以认为采集电流等价于单相励磁电流,实际上采用多相电流传感器的传统方案时,也选择忽略区域Ⅱ的重叠电流影响.
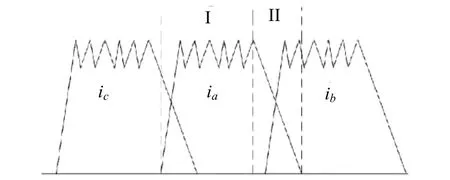
图4 三相电流非交叠波形Fig.4 three-phase current non-overlapping waveform
当出现双相导通驱动状态时,会出现前一相励磁电流和后一相励磁电流交叠情况.即“励磁重叠”状态,此时各相电流见图5.

图5 三相电流交叠波形Fig.5 waveform diagram of three-phase current overlap
图5中,区间Ⅰ、区间Ⅲ为励磁电流重叠区,其总电流和母线电流关系可表示为

为解决电流波形重叠问题,这里引入一种基于改进型转矩分配函数的方法,将重叠电流对转矩的影响通过转矩分配函数的构造过程予以消除.
由图6可知,每一相的期望转矩可以表示为位置角的函数,即
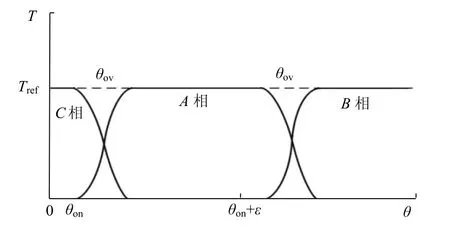
图6 转矩与位置角关系Fig.6 relationship between torque and position angle

式中,Tref(k)为总参考转矩;frise(θ)为导通阶段的上升沿TSF函数;fall(θ)为关断阶段的下降沿TSF函数,θon、θov、θoff分别为开通角、重叠角和关断角,rad.为寻求恒定转矩,frise(θ)、frise(θ)需满足
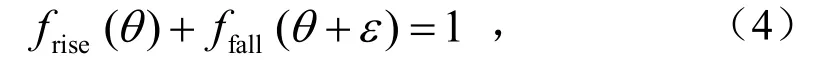
式中,ε=2πmNr为 SRM 极距角也称步进角,rad,其中Nr为转子极数,m为SRM的相数.
在多相电流采样控制时,重叠区的frise(θ)和ffall(θ)主要是用来解决换相区前后电感引起的转矩脉动问题.frise(θ)和ffall(θ)是电机的逆转矩模型函数,通常的做法是通过测量电机结构和材料参数,使用有限元仿真软件求出T-θ-i关系表并拟合出近似函数,这种方法不但需要大量仿真计算时间且受装配工艺精度等因素限制,结果与实际值偏差较大.
当采用母线电流采样法时,frise(θ)和ffall(θ)变成了同时补偿电机转矩误差和母线电流重叠影响的函数.同传统转矩分配函数法一样,改进后的转矩分配函数具体形式仍可以用直线型、三角函数型、指数型等形式.但由于总转矩不断变化和补偿母线重叠电流的影响,其函数结构形式上仍然与式(3)一致,但并不需要满足式(4)约束.以三角函数型为例,设

由于电机前后相电流在重叠区转矩贡献是变化的,但换相重叠区采集的母线电流信息却是代数和,没有相位信息,所以也采用不对称的frise(θ)和ffall(θ)来实现转矩的重新分配.由于两相励磁时磁能转换的机械能明显多于单相励磁时磁能转化的机械能,所以其转矩也大于单相励磁转矩,其具体值需根据不同电机具体情况,通过试验或有限元仿真计算获得.这里假设双相导通转矩为单相导通的 1.5倍,下面将通过搭建控制系统,验证减小转矩脉动的效果.
2 自抗扰速度环控制
2.1 自抗扰控制器结构
自抗扰控制是在继承了传统PID反馈控制思路的基础上,将控制系统的外部和内部扰动整合为总扰动的概念,并提出一种不依赖于被控对象的精确数学模型的扰动处理范式,结合现代控制理论提出的一种更易于与实践相结合的控制方法.自抗扰控制原理见图7.它由非线性跟踪微分器(nonlinear tracking differentiator,TD)、非线性误差反馈控制律(nonlinear error feedback control law,NLSEF)和扩张状态观测器(extended state observer,ESO)三部分组成[13].
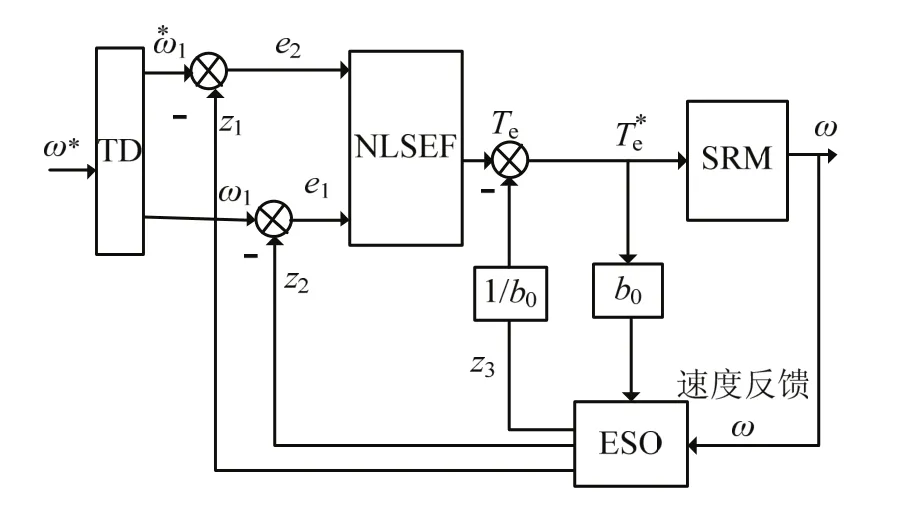
图7 自抗扰控制器原理Fig.7 schematic diagram of active disturbance rejection controller
非线性跟踪微分器(TD)的作用是通过过渡过程减小初始误差,降低初始阶段对系统的冲击、有效地解决超调与快速性矛盾.同时可利用其频率特性起到带通滤波器作用.
扩张状态观测器(ESO)是自抗扰控制器的核心控制部分,它以控制对象的输入和输出量作为依据,把状态的定义扩展到系统的总扰动,估算出系统的总扰动,并根据这些扰动量补偿到反馈中,从而消除扰动对系统实际特性的影响.
非线性状态误差反馈控制律(NLSEF)形式上可看作是某种PD控制器,引入了最速控制函数使误差以指数方式减小,并且能接受非线性状态反馈.
2.2 开关磁阻电机数学模型
开关磁阻电机的数学模型可由电压平衡方程、电磁转矩方程、机械运动方程组成,电压平衡方程为
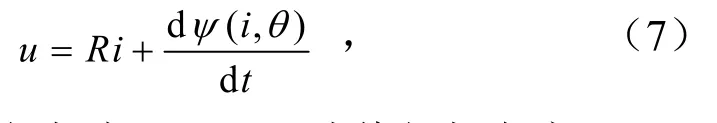
式中,u为绕组相电压,V;i为绕组相电流,A;R为绕组相电阻,Ω;ψ为绕组的磁链,Wb;θ为电角度,rad.
磁链方程为

电磁转矩方程为

机械运动方程
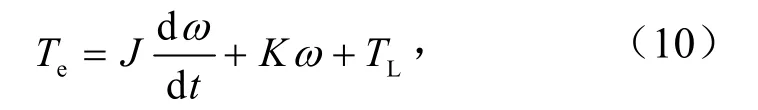
式中,J为转动惯量,kg·m²,K为阻尼系数;TL为负载转矩,N·m;Te为电磁转矩,N·m;L为绕组电感,H;ω为电机转速,r/min.
2.3 开关磁阻电机自抗扰控制器设计
为便于理解分析,将开关磁阻电机数学方程转换为自抗扰范式的线性差分方程,首先将式(10)转化为

进一步将方程右侧前两项合并为
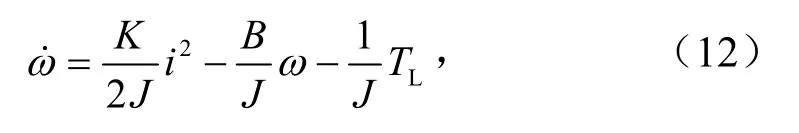
将其与一阶系统状态方程对应得到


式中,Lmax、Lmin为电感的最大和最小值,H;θup为电感上升区区间范围.在小电流运行时由于电感饱和效应不明显,可以假设K为常数[14].为得到电流输入形式,需要将控制器输出i2再开根号转换为标准电流i.
为方便分析,将转速ω作为控制目标,则被控系统可以当作成一个一阶系统.取电机的给定转速ω为输入,通过TD滤波器得到合适的过渡过程ω1和ω2,TD滤波器线性差分方程为

式中,
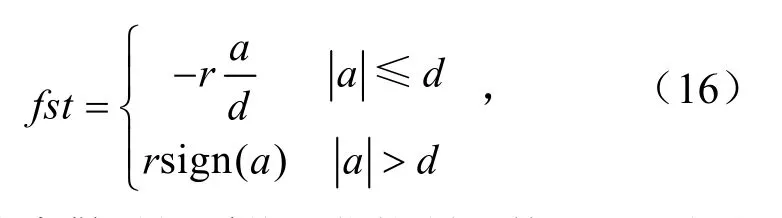
其中,fst为离散时间系统最优控制函数;sign为分段函数;d=rh,r为跟踪速度参数,r越大跟踪效果越好.以电机的实际转速ω为输入信号,设计二阶扩张状态观测器,将反馈差值e处理后,得到的ω观测值和系统所受总扰动的估计值方程为
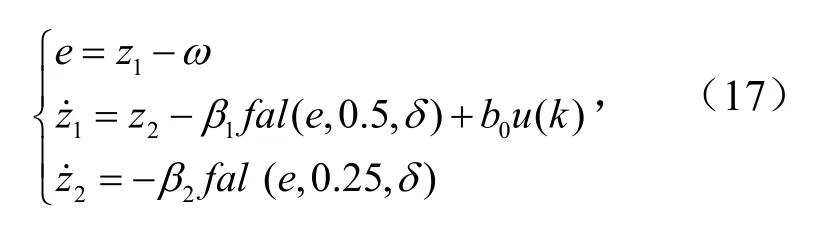
式中,β1、β2为反馈增益,其取值影响ESO的收敛速度,当h大于0.01时,β1一般取积分步长h的倒数,β2取作为补偿因子.fal为非线性函数,其表达式为
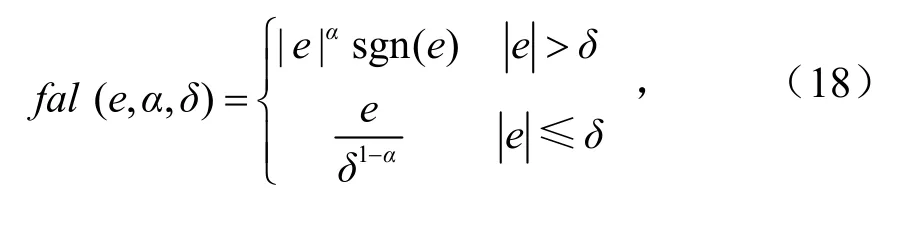
式中,e为误差信号;α为滤波因子;δ为线性区间的宽度,这里取经验值0.01.
由给定转速ω1的跟踪值和实际转速ω的观测值z1得到状态误差e1.
采用fal函数构成非线性状态误差反馈控制律
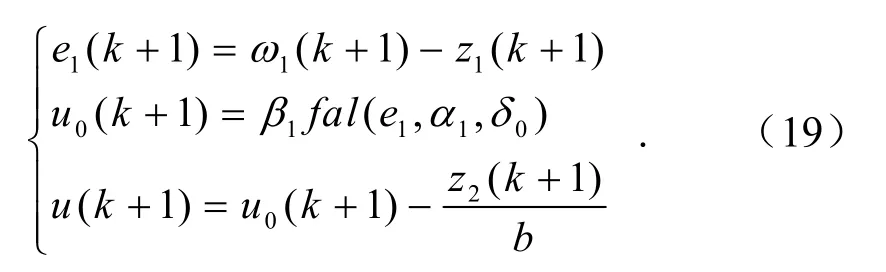
再由ESO实时估计出的扰动进行补偿,得到最终的输出控制量为

式中,u0=β1fal( −y1(k),α0,δ0)为非线性反馈;Z2为内部和外部扰动的补偿.
3 抗饱和PID电流闭环控制
传统开关磁阻电机电流环通常采用滞环控制方式,其优点是程序结构简单、适用性强.但在实际运行时存在两方面问题,其一,当电机处于低转速、低转矩时电流变化情况很小,这就要求滞环限宽设置得足够小,这对电流传感器精度和采样电路设计要求较高;当电机处于高转速情况下,电流滞环控制法控制精度明显不足,又需要引入角度控制技术和高精度编码器,这样又提高了系统成本.其二,现代数字控制器多采用多路 PWM 发生器作为主要驱动输出器件,而滞环控制这种控制方式即不能充分利用控制器的带宽资源,也不利于开发人员编写控制程序.故本文采用抗饱和PID代替滞环控制作为电流环控制器,不但降低了采样电路精度需求,充分利用数字控制芯片性能,且能使绕组电流变化更加平滑,实际使用中在相同开关频率下dv/dt更小,器件所受冲击明显降低,延长了器件使用寿命.比较各种抗饱和PID结构后,这里采用带有积分反馈抑制抗饱回路的PID控制器作为电流环控制器,其基本思想简单来说就是当饱和出现时,对积分项加入负反馈,使其尽快退出饱和.抗饱和PID结构见图8.
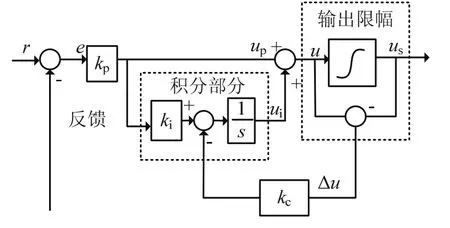
图8 抗饱和PID结构Fig.8 Anti-saturation PID structure
当系统发生正向饱和,则u>umax,那么有Δu=u-us>0,所以最终Δu将反馈到积分部分;相当于从ui中减去了Δu,这样可以对积分项进行削弱,使其退出饱和状态;抗饱和系数Kc越大,积分器退出饱和响应越快,反之则越慢;通常Kc的取值范围为0.3~3倍的Ki/Kp.实际调试过程中应根据饱和情况进行适当调整.
4 仿真与实验
4.1 仿真验证
在Matlab R2020a环境下搭建单电流传感器母线电流采样开关磁阻电机调速系统模型,通过仿真验证方案可行性.
为使仿真得到的结果尽可能接近实际,对实验平台开关磁阻电机各项参数进行估测,实际电机为12/8三相开关磁阻电机,参照材料密度表和转动惯量公式估算出转子转动惯量J约为0.05 kg·m².根据文献[15]提出方法测量电感变化范围在 0.013 H至0.005 H.实际驱动电路限压为20 V,限流为20 A.电机铭牌和估测参数见表1.

表1 电机参数Tab.1 motor parameters
调速系统结构见图9,包括开关磁阻电机模型、自抗扰调速控制模块、电流环控制模块、不对称半桥驱动模块、速度检测模块等.
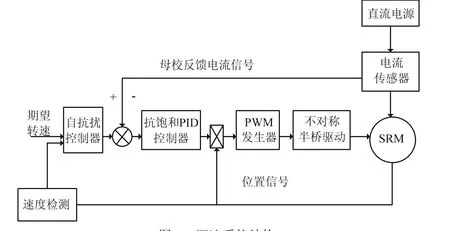
图9 调速系统结构Fig.9 structure of speed control system
图10为单步换相母线电流和三相采集电流波形对比,红黄蓝为A、B、C三相电流,可以看出母线电流完整保存了各相电流信息,不存在电流重叠,可直接作为电流反馈使用而无须进行任何补偿.
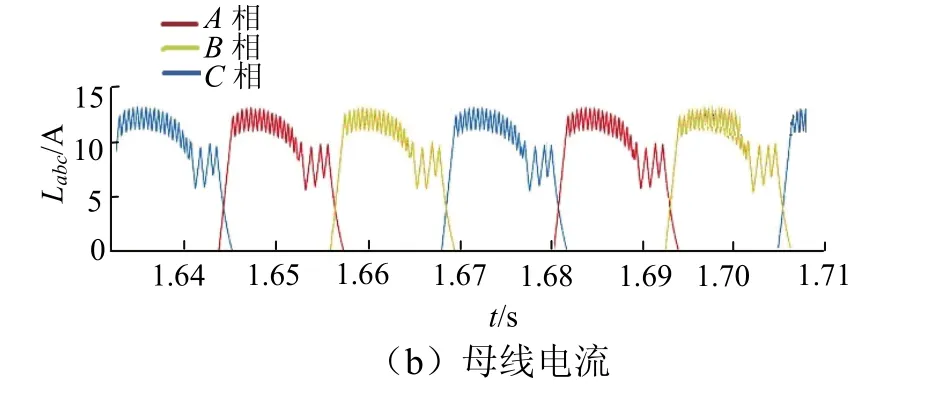
图10 不同导通角电流对比Fig.10 comparison of current at different conduction-angle

图11给出无交叠导通角和全导通角母线采样法的两种导通角稳态转矩对比.传导交叠并未影响系统的转矩调节能力.且全导通输出总转矩更高,转矩连续性更强.
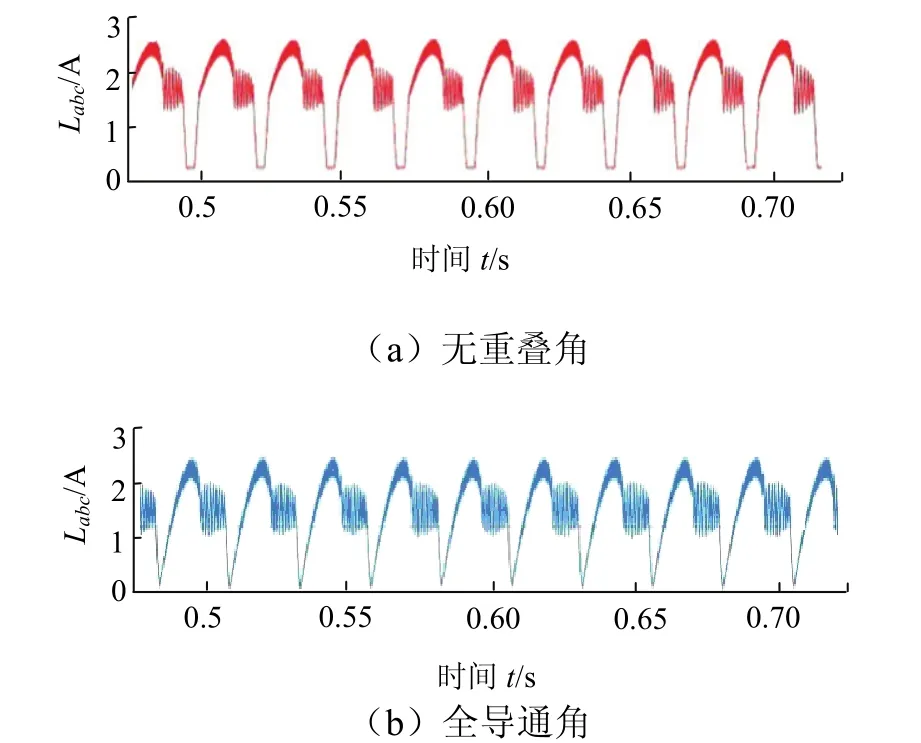
图11 不同导通角转矩对比Fig.11 comparison of torque at different conduction angles
图12给出了自抗扰和PID两种控制器组合调速仿真对比图,可以发现与传统PID调速控制器相比自抗扰调速控制器的跟踪能力有一定提升,且稳态误差明显降低.
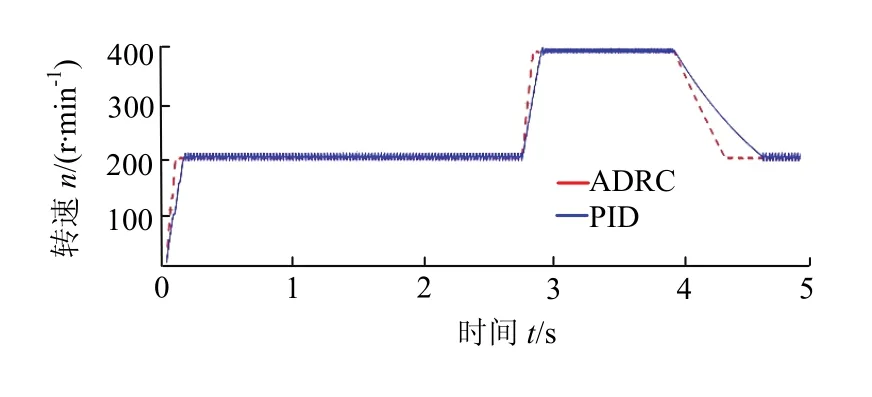
图12 ADRC和PID控制调速对比Fig.12 comparison of ADRC and PID control speed regulation
图13还对比了自抗扰和一般PID速度控制器两者的抗扰动性能,在2 s时给予两者相同的人工干扰,仿真表明两者都有一定的抗扰能力.
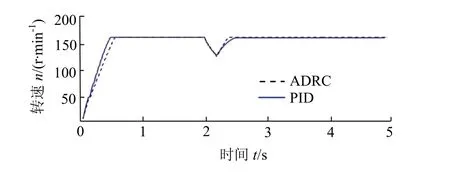
图13 自抗扰与PID控制抗扰动性能对比Fig.13 comparison of ADRC and PID disturbance rejection performance
为测试改进型转矩分配函数处理励磁重叠电流影响的能力,搭建了基于母线电流采样法和改进型转矩分配函数法的电机调速模型,见图14.

图14 改进型转矩分配函数调速系统模型Fig.14 improved torque distribution function speed regulation model
转矩脉动系数定义
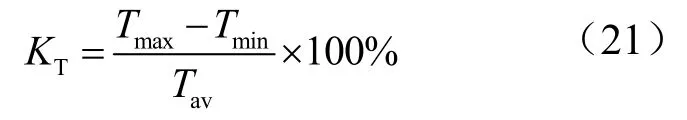
式中,Tmax、Tmin、Tav分别为电机进入稳态后的最大电磁转矩、最小电磁转矩、平均电磁转矩,Tav可以由速度控制输出的参考转矩Tref近似替代.转矩分配改进前后转矩见图15.

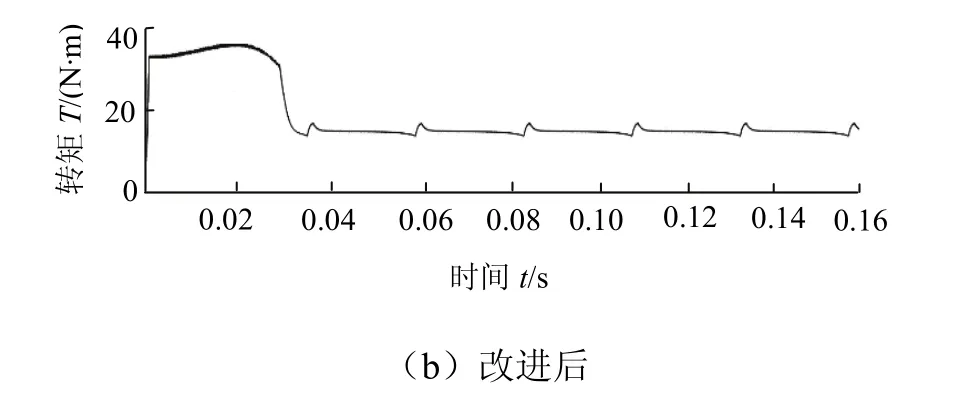
图15 转矩分配改进前后转矩Fig.15 torque before and after improvement of torque distribution
由图15可知,采用改进型的转矩函数后转矩脉动明显降低.转矩脉动系数从传统三角函数法的0.52降低到0.43.
4.2 实验结果分析
采用Simluink自动代码生成功能,将仿真系统中的模型代码下载到 DSP中进行实验验证.实验设备包括:笔记本上位机;DSP F28335开发板,不对称半桥驱动电路,12/8开关磁阻电机,霍尔电流传感器,可编程直流电源,数字示波器.软件开发环境为:Matlab 2020a;CCS 6.0.实验平台见图16,实验结果见图17~图22.

图16 实验平台Fig.16 experimental platform
图17、图18为滞环电流和抗饱和PID控制的电流。对比图17、图18可以发现外部因素完全相同的情况下,抗饱和PID作为电流环控制器相比于传统滞环控制电流波形更平稳和光滑.从图18可以看出母线电流波形基本等于各相电流波形之和,说明各相电流能被准确采集,保证了电机运行可靠性.
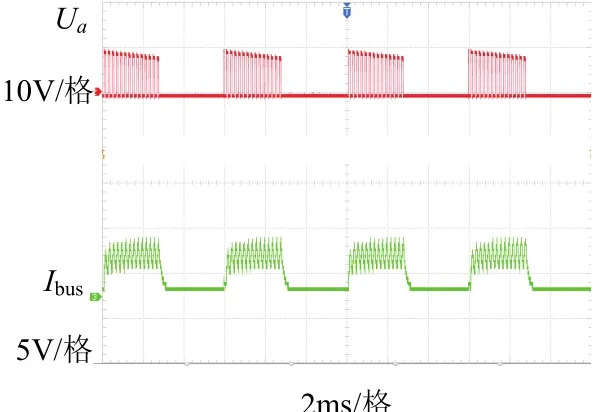
图17 滞环控制电流Fig.17 hysteresis control current
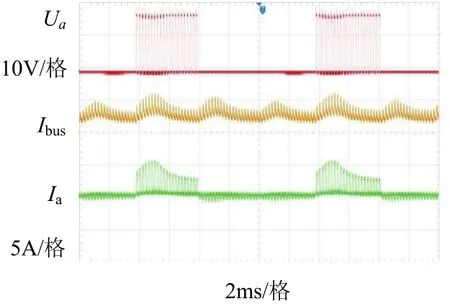
图18 抗饱和PID电流Fig.18 anti saturation PID current
PID控制和自抗扰控制两者实际调速性能对比见图19,从图中可以发现两者均有良好的转速跟踪能力,自抗扰拥有更好的稳态性能.
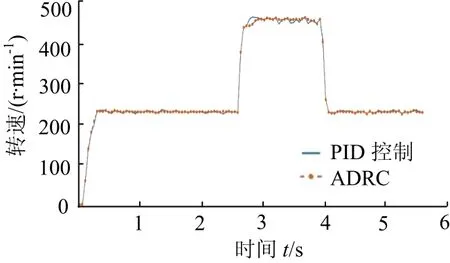
图19 实际调速性能对比Fig.19 speed control performance comparison
图20为PID和ADRC速度控制器性能对比,可以看出PID与ADRC两者都有一定的抗扰能力,ADRC拥有更强的调节能力,受扰动后未出现明显的超调,鲁棒性更强.由于硬件条件的限制,实验仅验证了两相启动模式母线采样方案在励磁电流重叠情况下的有效性.
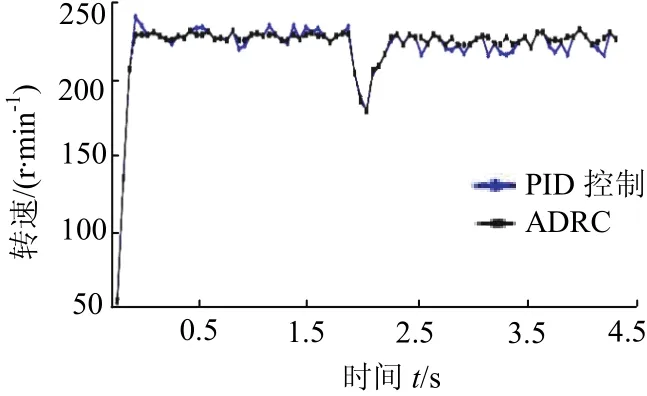
图20 抗扰动性能对比Fig.20 anti-disturbance performance comparison
图21为两相启动的母线电流和相电流,图22为两相启动转速波形.可以看出由于电流交叠和互感的原因,母线电流无法归零,这与仿真结果一致,母线采样电流仍能实现电机启动和速度调节.
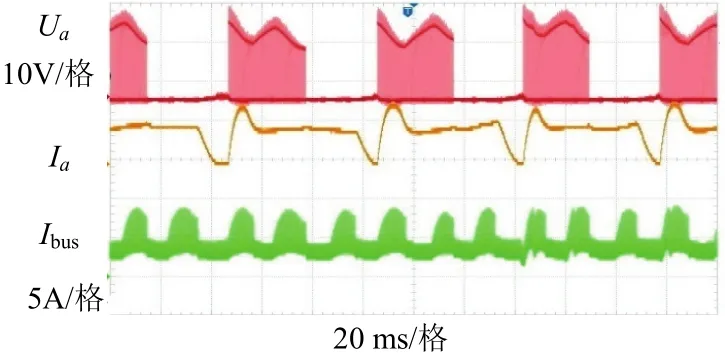
图21 两相导通电流Fig.21 two phase conduction current
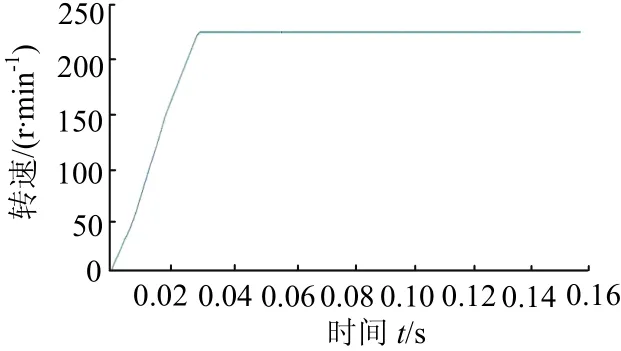
图22 两相启动速度Fig.22 Two-phase starting speed
5 结论
本文分析基于母线电流采样的开关磁阻电机的调速方法,通过仿真与实验分析,得出如下结论.
(1)母线电流采样方案,在单通道换相运行条件下,各相电流采集互不干扰,仿真与实验结果一致,该方案简化了硬件结构,降低了硬件成本和控制算法的复杂性,降低了故障发生率,更利于保障人员和设备的安全,对于小功率和低成本的应用场景具有一定的商业价值.
(2)自抗扰控制技术在开关磁阻调速系统中具有良好跟踪性能和抗扰动性能,有一定的降低转矩脉动能力.
(3)针对双相导通时母线电流采样带来的电流重叠问题,本文所提出的改进型转矩分配函数法具有一定的降低转矩脉动的能力,且改进空间较大.
