基于振动频移的纤维增强复合材料薄板裂纹识别
2022-09-22屈建龙徐成辉周震寰徐新生
屈建龙,徐成辉,王 伟,周震寰,徐新生
(1.大连理工大学 工程力学系,辽宁 大连 116024;2.西北工业大学 力学与土木建筑学院,陕西 西安 710072)
0 引言
自然纤维增强复合材料因其重量轻、生物降解性好、比强度高等优点,被用于制造梁、板、壳等基本构件,广泛应用于航空航天、建筑、核工业等领域[1],针对这种材料也产生了许多强度理论[2].通常情况下,结构中的裂纹会引起强度和刚度的损失,导致结构的固有振动频率和模态振型发生变化.因此可以根据损伤前后振动参数的变化来进行结构的裂纹损伤检测[3].对于结构损伤识别问题,可通过分析含裂纹结构的频移,检测出裂纹的几何尺寸和位置等[4].采用固有频率频移原理,对梁裂纹参数识别问题的研究已经比较成熟,但对于板类结构的损伤识别研究[5]尚待深入.由于纤维增强复合材料板的广泛应用,建立其损伤或裂纹识别方法越来越重要.针对含裂纹自然纤维增强复合材料薄板结构,采用线弹簧模型理论和哈密顿体系相结合的方法,获得薄板结构自由振动频率和模态函数的解析解,并根据频移可对裂纹的位置和长度进行识别.
1 基本问题
考虑中心开裂的自然纤维增强复合材料薄板,板的长、宽、高分别为a、b、H,见图1.自然纤维的方向与x轴平行,坐标系位于板的中面.裂纹的长度为ac,与x轴平行,裂纹中线和板中面的距离为d,见图1(b).考虑裂纹深度hc,裂纹高度与板厚之比为s=hc/H.当d/H= 0 时,为中心对称裂纹;当d/H= ( 1 −hc/H)/2时,为表面裂纹;当0 图1 含中心裂纹自然纤维增强复合材料薄板Fig.1 schematic diagram of natural fiber reinforced composite plate with a central crack 自然纤维材料性质受湿热老化的影响,采用文献[1]的力学性质老化模型,得到自然纤维增强复合材料薄板的材料参数为 式中,E11、E22为杨氏模量;G12为剪切模量;υ12为泊松比;f为纤维板中纤维质量分数;γs和γl为描述吸水和湿热老化的函数,无量纲,与剪切模量G、纤维含量f和老化时间t密切相关.剪切模量G,GPa, 老 化 时 间γl=−fTte xp(−fTt) − e xp(−fTt)+ 1 ; 密 度 为kg/m3.这里ρ0是初始时刻(t= 0)的密度.相关计算参数[1]可以通过与实验数据的曲线拟合方式获得:G= 0.104GPa,= 9 0.870,= 7.3459,= 2 00.0104,χs= 0.6171,D= 5 6.18hN/m2和T= 0.1/h,其中为无量纲参数,有关参数的具体含义可参考文献[1]和文献[6]. 根据薄板理论和线弹簧模型(LSM),含裂纹纤维增强复合材料薄板的动力学方程可以表示为[7] 由裂纹引起的力和弯矩可以利用线弹簧模型得到.线弹簧模型的核心思想是建立裂纹位置和板边的拉伸和弯曲力之间的关系.该关系可以表示为这里 其中,αbb、αtb和ttα分别表示裂纹中心的弯曲、拉伸弯曲和拉伸裂纹柔度系数.这3个系数是裂纹深度、板厚和裂纹位置的函数,可以通过曲线拟合应力强度因子形状函数获得[8]. 含裂纹复合材料矩形板的边界条件可以表示为 ①简支边界条件(S) ②固支边界条件(C) ③自由边界条件(F) 式中,剪力Vx和Vy为 其中,d1=D12+ 4D66. 为了导入含裂纹复合材料薄板振动问题的哈密顿对偶方程,将y模拟时间坐标,即并记 ∂ /∂x=∂x.定义状态向量为 式(8)为哈密顿对偶方程,其中哈密顿算子矩阵H及相应的子矩阵为 式 中 ,κx1=D11(1 −ξMx),κx2=Nx(1−ξMx),κ=−ρHω2(1 −ξ),κ=− (D+ 4D)(1 −ξ) x3Mxx41266Mx和κx5=−Ny(1 +ξNx)(1 −ξMx). 为了哈密顿对偶方程的求解,考虑对边(x= 0和x=a)简支边界条件.哈密顿对偶方程可以通过分离变量法求解. 假设Ψ(x,y) =ψ(x) exp (μy),得特征方程为 式中,μ和ψ分别为辛本征值和本征解. 利用x= 0和x=a边简支边界条件,得到本征值和本征解为 式(10)、式(11)中,n= 1 ,2,3,…,和αn=nπ /a.状态向量可以表示为本征解 式中,μn2=−μn1,μn4=−μn3;cni为未知系数,可以通过y= 0和y=b的边界条件确定. 将对应于y= 0和y=b的边界条件代入式(12),得到不同边界条件下含裂纹自然纤维增强复合材料薄板的固有频率方程. (1)简支-简支(SSSS) 对于四边简支的含裂纹自然纤维增强复合材料薄板,将式(12)代入式(3),得到频率方程为 (2)固支-固支(SCSC) 对于对边简支另一对边固支的含裂纹自然纤维增强复合材料薄板,利用式(4)得到频率方程为 (3)简支-固支(SSSC) 对于三边简支另一边固支的含裂纹自然纤维增强复合材料薄板,借助于式(12)、式(3)和式(4),频率方程可以写为 (4)自由-自由(SFSF) 对于对边简支另一对边自由的含裂纹自然纤维增强复合材料薄板,将本征解式(12)代入边界条件式(5),得出频率方程为 (5)简支-自由(SSSF) 对于三边简支另一边自由的含裂纹自然纤维增强复合材料薄板,频率方程可通过式(12)、式(3)和式(5)得到 (6)固支-自由(SCSF) 对于一对边简支另一对边固支和自由的含裂纹自然纤维增强复合材料薄板,将式(12)代入边界条件式(4)和式(5),频率方程可表示为 将计算出的频率代入相应边界条件方程,从而可以得到关于式(12)中未知系数cni的代数方程组,并确定出各未知系数.此时,本征解可以直接表示为模态函数. 为验证辛方法的准确性,与其它文献进行对比.考虑含裂纹各向同性矩形薄板,H/a= 0.01,泊松比υ= 0.3.文献[7]、文献[8]前2阶固有频率与本文辛方法算出的频率对比见表1.从表1中可以看出,本文计算结果与文献[7]、文献[8]给出的结果在不同裂纹长度下的固有频率相吻合.从上述对比算例可知,辛方法在求解含裂纹矩形薄板自由振动问题是有效和可靠的. 表1 不同方法前2阶固有频率对比Tab.1 comparisons of the first two natural frequencies that calculated by different methods 下面将讨论不同边界条件下,自然纤维增强复合材薄板振动频率在不同参数变化下的改变情况,在计算中取H/a= 0.05.当薄板中自然纤维的含量f为10%,老化时间t等于100 h时,图2和图3分别给出了前2阶含裂纹薄板频移随裂纹长度和深度的变化情况.从图2和图3中可见,频移随裂纹长度的增大而增大,随裂纹深度的增大而减小;内裂纹(d/H< 0.2)和表面裂纹(d/H= 0.2)的频移趋势明显不同.对于内裂纹,裂纹长度ac/a< 0.1时,频移急剧增大,频移对微裂纹非常敏感.而表面裂纹随裂纹长度增大的趋势比较平缓.还有频移在裂纹深度d/H> 0.15时,有突然急剧减小的趋势,这是因为在d/H≥ 0.15时,3个裂纹系数αbb、tbα和ttα突然增大导致薄板的刚度发生突变[9].本算例表明,可以结合前 2阶频率的频移的变化情况,对自然纤维增强复合材料薄板的裂纹长度和深度进行损伤识别. 图2 含裂纹SSSS薄板频移随裂纹长度和深度的变化Fig.2 variation of frequency shift versus crack length ratio and crack depth ratio for the cracked SSSS plate 图3 含裂纹SFSF薄板频移随裂纹长度和深度的变化Fig.3 variation of frequency shift versus crack length ratio and crack depth ratio for the cracked SFSF plate 此外,研究不同裂纹长度和自然纤维含量下,含中心对称裂纹(d/H= 0)SCSC自然纤维增强复合材料薄板频移随老化时间的变化情况,见图4.从图4中可以看出,当薄板中自然纤维含量较低时(f=5%),频移的变化趋势单调下降,最后趋于平稳;当自然纤维含量较高时(f= 15%),频移随时间的增大,先下降然后增大最后趋于平稳.这是由于自然纤维材料吸水,密度随时间先增大,然后由于湿热老化,密度随时间而减小,最后老化时间很长时,密度接近一定值.在这种情况下,密度和弹性模量几乎保持不变.本算例表明,自然纤维的含量对薄板频移的影响很大.因此,在对自然纤维增强复合材料薄板裂纹进行识别时,应该先评估自然纤维的含量. 图4 含裂纹SCSC薄板频移随老化时间的变化Fig.4 variation of frequency shift versus ageing time for the cracked SCSC plate 利用线弹簧模型和辛方法,可将含裂纹自然纤维增强复合材料薄板固有频率和振型问题归结为哈密顿体系下的辛本征值和本征解问题.在哈密顿体系下,可直接获得含裂纹纤维增强复合材料薄板的固有频率和模态函数的解析解,以及频率方程表达式.通过数值结果对比表明,辛方法具有较高的计算精度.研究结果表明,振动频移随板中自然纤维的含量,老化时间和裂纹长度与深度的变化而改变.频移随裂纹长度的增大而增大,随裂纹深度的增大而减小.因而,可根据频移规律识别相应裂纹的位置和长度等.该方法为纤维增强复合材料薄板的裂纹或损伤的识别提供一种方法和依据.

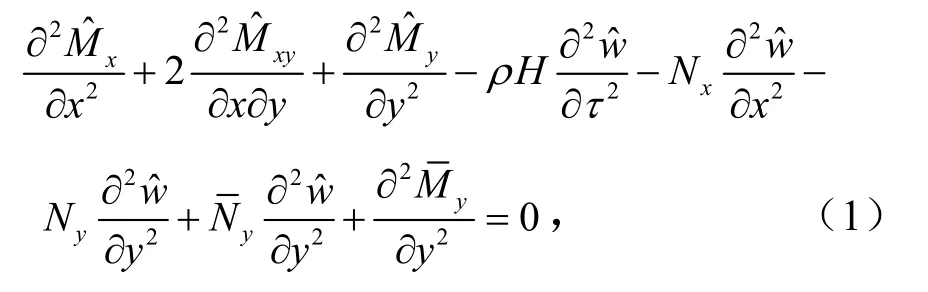




2 导入哈密顿体系






3 振动频率方程






4 数值算例与分析




5 结论
