基于共空间模式和均匀流形投影的运动想象脑电信号识别方法
2022-09-21付荣荣隋佳新
付荣荣,隋佳新,刘 冲,张 扬
(1.燕山大学 电气工程学院,河北 秦皇岛 066004;2.东北大学 机械工程与自动化学院,辽宁 沈阳 110819;3.沈阳机床(集团)有限责任公司 设计研究院,辽宁 沈阳 110142)
1 引 言
运动想象脑电数据的特征提取以及分类工作逐渐成为了脑机接口领域研究的热门话题。在进行脑电数据的特征提取及分类时,常常面临着由于脑电数据维数过高从而导致计算量巨大的问题。为了能够从夹杂着大量杂乱信息的高维数据中提取出想要的脑电数据的特征和规律,直接使用常用的在低维空间内部表现优异的机器学习算法进行数据降维,得到的效果就差强人意了[1]。此时,数据降维技术不仅能解决高维数据带来的计算量大、复杂性高的问题,还能将高维数据可视化,从而在低维空间直接观察数据在高维空间的分布情况,更利于数据特征的提取与分类。目前,经典的数据降维方法包括线性判别分析、主成分分析和多维尺度分析等[2]。这些传统方法虽然能够通过对样本的特征进行线性组合来发现数据中的线性结构,但是脑电数据中包含了大量的非线性特征,在对非线性特征的处理上,上述方法就显得有些不足了[3]。
2000年Seung H S等发表了题为The manifold ways of perception的文章,首次提出了流形学习的概念,并指出人类的感知是以流形为基础的,高维结构可以通过低维变量表示出来[4]。随后大量的流形学习的算法涌现,并开始在数据降维、图像处理等领域快速发展。流形学习算法本质上就是模仿人类的神经感知系统,其基本思想为:假设所研究的数据集均匀采样于高维数据空间中的流形结构上,在保持数据集之间邻域关系不变的基础上,找出隐藏于高维观测数据空间中的低维流形结构,并将这种从高维观测空间到低维嵌入空间的非线性映射关系通过某种方式构造出来,从而达到数据降维或者可视化的目的[5]。目前,常用的流形学习算法包括局部线性嵌入、等度量映射、t-SNE等[6]。本文区别传统的流行学习算法,将共空间模式算法和均匀流形投影算法相结合,应用于运动想象脑电信号的数据降维和分类中,该方法充分利用了脑电数据的非线性特征,降低了在脑电数据分类过程中的计算复杂度,有效提高了分类的准确率,并且在特征数据可视化方面也有着不错的效果。
2 数据来源及预处理
本文数据来自实验室面向运动耦合约束的交互实验[7]运动想象脑电数据,受试者为10名健康的22岁到30岁的大学生,实验使用Emotive Epoc+14导联脑电采集设备对受试者脑电进行采集,采样频率为128 Hz,受试者通过点击键盘左右键来控制电脑屏幕中的碗状结构向左或向右移动,碗中小球也会同时因为惯性在碗中左右运动,在保证碗中小球不从碗中掉落的前提下,将碗从起点运送到终点,进而在碗状结构左右运动时可以分别得到左手和右手的运动想象脑电数据。采集到原始数据后,将数据按照实验次数每秒钟逐次截段,存储为高维形式(样本数×导联数×试验数×类别数)。
3 算法原理
3.1 共空间模式
共空间模式算法(common spatial pattern,CSP)是一种空域滤波特征提取算法,主要针对二分类任务[8]。CSP算法主要通过创建一个最优的公共空间滤波器,对两类数据的协方差矩阵进行对角化,得到差异最大化的两类方差,进而得到特征向量。
3.1.1 计算两类数据的协方差矩阵
将运动想象脑电数据分为E1和E2两类,其中E1表示左手运动时脑电数据,E2表示右手运动时脑电数据。计算协方差矩阵的公式如下:
(1)
式中:trace(E)表示求矩阵E的迹。
由式(1)可以得到:
C=C1+C2
(2)
式中:C表示两类数据的空间协方差矩阵之和。
3.1.2 求出白化值矩阵并做对角化
求正定矩阵C的特征向量和特征值,即:
C=UΛUT
(3)
式中:U为特征向量矩阵;Λ表示特征值的对角阵。对矩阵U进行白化处理可以得到:
(4)
3.1.3 计算投影矩阵得到特征矩阵
对C1和C2进行如下变换:
S1=PC1PT=BΛ1BT
S2=PC2PT=BΛ2BT
(5)
由式(5)可知,当S1特征值最大时,对应的S2有最小的特征值,故可以通过特征向量矩阵Q实现数据的分类,得到投影矩阵:
W=(QTP)T
(6)
进一步得到特征矩阵:
Z=W·E
(7)
3.2 均匀流形投影算法
均匀流形投影算法(uniform manifold approximation and projection for dimension reduction,UMAP)是基于流形学习的一种非线性数据降维方法[9]。脑电信号是一种非平稳性强、随机度高、高度非线性的生物电信号。如图1所示,在多维空间中,两个点之间的欧氏距离,即直接连接的距离很近,但是如果上升到流形的理论,其连接距离就不再是直线连接,而是流形表结构上的距离[10]。在高维空间中所观察到的数据从局部来看,可以近似地视为是符合欧式分布的,故只有在进行流行局部分析时,欧式距离才会更接近真实距离。因而,这种基于流形学习的方法能更精准地挖掘出特征数据真实信息。均匀流形投影算法主要分为构建初始模糊拓扑表示和优化低维嵌入两个部分[11]。

图1 多维空间流形距离示意图Fig.1 Schematic diagram of multi-dimensional space manifold distance
3.2.1 获取低维表示
假设脑电数据集来自一个拓扑空间,首先生成该空间的开覆盖,进而了解该空间的拓扑,构造单纯复形。采用最邻近下降算法,给定一个超参数k,k用来表示xi所具有的k个邻居,进而得到每个xi的k最近邻集合{xi1,…,xik}。对于每个xi,进而确定其对应的ρi和σi:
ρi=min{d(xi,xij)|1≤j≤k,d(xi,xij)>0}
(8)
(9)
进而得到条件概率表达式为:
(10)
pij=pi|j+pj|i-pi|jpj|i
(11)
式中:pij为条件概率,用来表示数据点xi和xj之间的相似度,pij越大则说明两个点之间的相似程度越高,越有可能为同一类数据。
最终得到低维空间表示为:
qij=(1+a(yi-yj)2b)-1
(12)
式中:a和b为超参数,一般情况下取a=1.93,b=0.79。
3.2.2 优化低维嵌入
对已经计算好的模糊拓扑表示进行优化,使高维和低维具有尽可能接近的模糊拓扑表示。这里,使用交叉熵来衡量两种表示的近似度,运用随机梯度下降法对低维嵌入进行优化,交叉熵的公式如下:

(13)
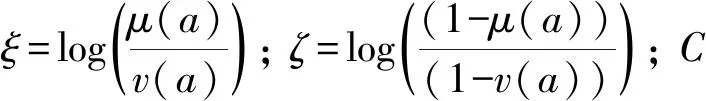
4 实验结果与分析
本文中选取了10名受试者的脑电信号进行特征提取和降维研究,脑电信号的整体处理流程如图2所示。
4.1 不同受试者运动想象脑电数据分类结果
在对脑电信号进行特征提取和降维的过程中,为了保证结果的稳定性,降低随机性的影响,通常将数据集分为测试集和训练集两个部分,使用交叉验证的方法对数据进行处理。本文采用了10折交叉验证的方式,将10个受试者的运动想象脑电信号数据分为测试集和训练集,用CSP进行特征提取,UMAP进行数据降维,最后使用KNN分类器实现数据分类,其交叉验证结果如表1所示。

表1 不同受试者脑电数据交叉验证结果Tab.1 Cross-validation results of EEG data of different subjects
表中:ACC表示分类的准确度;AUC为受试者工作特性(ROC)曲线与坐标轴围成的面积;ACC和AUC的值越接近1,说明分类效果越好。
从表1中可以看出,5位受试者的ACC的均值为0.961 6,AUC的均值为0.951 7。由此说明,经过特征提取和UMAP算法降维的运动脑电数据的分类效果很好。
脑电信号处理整体流程如图3所示。

图2 脑电信号处理整体流程图Fig.2 Overall flow chart of EEG signal processing
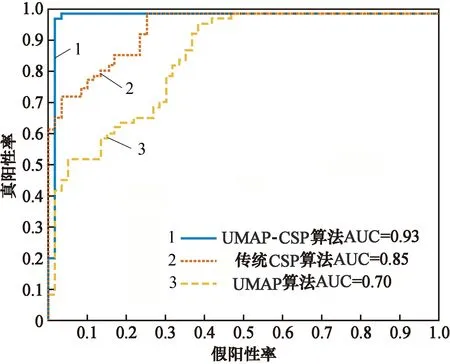
图3 3种方法KNN分类器分类ROC曲线对比图Fig.3 Comparison of ROC curves of three methods KNN classifier classification
4.2 脑电数据降维前后分类效果对比
本文在运动想象脑电数据的分类工作中首次使用了传统CSP算法和UMAP算法相结合的方式,对脑电数据进行了特征提取和数据降维工作。与传统的单纯CSP算法相比,大大减小了数据分类过程的计算量。
将本文中CSP-UMAP算法与传统的CSP算法对分类结果的影响相比较,传统的CSP算法在进行特征提取后一般取特征矩阵的头部和尾部的特征,直接进行分类;而本文则在CSP算法后加入了UMAP算法,在降低计算量的同时,充分利用了特征矩阵的所有特征。对受试者A的脑电数据分别进行传统CSP算法的特征提取和本文采用的CSP-UMAP相结合的方式,使用KNN分类器进行分类得到的ROC曲线结果如图4所示。

图4 UMAP算法特征数据可视化效果对比图Fig.4 UMAP algorithm feature data visualization effect comparison chart
从图3中可以直观地看出,未经过降维算法处理,直接使用传统CSP算法进行特征提取的脑电数据直接分类的ROC曲线图的下方面积明显小于经过UMAP算法降维之后的ROC曲线图的面积。由此可知,相比于传统的CSP算法而言,本文采用的CSP-UMAP算法相结合的方法在降低计算量的基础上,充分利用了特征矩阵的全部特征,起到了提高分类效果的作用。
4.3 UMAP降维算法在数据可视化方面的表现
在数据降维过程中,本文采用了UMAP流形学习算法对数据进行降维处理以达到降低分类计算量、提高分类精确度的目的。由于脑电数据中蕴含着大量的非线性特征,因而传统的线性降维方法无法保证在数据降维前后、在保证脑电数据点之间距离信息的同时,找到数据的合适的低维表达。与传统线性降维方法不同,UMAP是一种非线性的降维方法,该方法充分利用了脑电数据中的非线性特征,充分保证了数据降维前后的距离信息,在数据特征可视化方面有很大的优势。对受试者A和B的脑电数据进行降维,将数据维度降低至2D,与未降维之前进行对比,得到散点图如图4所示。
如图4所示,图中圆点分别表示受试者A和受试者B未经降维和经过UMAP算法降维后脑电数据在二维空间的分布位置,从图(a)和图(c)中可以看出受试者A和B未经过降维的脑电数据的散点图十分杂乱,难以分辨出不同类别,然而从图(b)和图(d)中可以看出,经过UMAP算法降维的脑电数据的散点图左右手脑电数据被明显分为两类,大大提高了脑电数据特征的可视化程度。
5 讨 论
在运动想象脑电信号中蕴含着大量的非线性特征,本文将CSP算法和UMAP算法相结合,运用于运动想象脑电数据的分类工作中,提供了一种快速高效的脑电信号特征提取和降维方法。对采集的运动想象脑电数据进行了特征提取和数据降维工作,并且使用KNN分类器对脑电数据进行了分类,经过交叉验证检验,发现分类准确率达到了90%以上。进一步将CSP-UMAP算法与传统的CSP算法进行对比,通过绘制ROC曲线的方法,对分类效果进行评估。2011年,Arvaneh M等[12]和Shi L C等[13]将CSP算法应用于第Ⅳ届BCI竞赛的数据集I中[14],对脑电信号进行了分类研究,该数据集记录了4名受试者依靠电脑提示进行左右手运动想象的脑电数据。相比他们的研究成果,本研究中分类的准确率大约分别提高了3.3%和7.2%。这体现了与传统的CSP算法相比,CSP-UMAP算法充分利用了脑电数据的非线性特征,在降低分类计算量的同时,大大提高了分类器的分类效果。与此同时,在脑电特征数据可视化方面[15~18],CSP-UMAP算法能直观观察脑电信号的特征数据在二维空间的分布状态。这不仅为研究者从低维空间中的少量特征数据为切入,进而研究存在于高维空间的大量数据提供了一种新的解决方案,更可以通过低维数据所具有的聚类性和可分性将其应用于脑电信号的分类工作,为从运动想象脑电数据在低维空间分布特性的角度,对脑电信号和运动想象任务之间的关系和规律进行分析和研究,为进一步揭示脑电信号的本质特征提供了一种新思路。
6 结 论
本研究提出了基于CSP-UMAP算法的运动想象脑电信号识别方法,实验数据采用实验室采集的面向运动耦合约束的交互实验的运动想象脑电数据,使用CSP-UMAP算法对运动想象脑电数据进行特征提取和数据降维,并使用KNN实现了特征分类,通过交叉验证的方式验证了算法的稳定性,并对结果进行了评价,最后还研究了在脑电特征数据可视化方面CSP-UMAP算法的表现。实验结果表明,将CSP算法和UMAP算法相结合应用于运动想象脑电数据特征提取和数据降维中,可以有效提高脑电数据分类的识别效果,并且在脑电数据特征可视化方向有着不错的表现。
