富水圆砾地层斜向并行隧道上部盾构掘进对下部管片力学状态的影响

倪准林，王树英，黄硕，瞿勇，刘奥林

(1.中南大学土木工程学院，湖南长沙，410075；2.北京大学工学院，北京，100871)

当前城市地铁隧道大多采用盾构法施工，随着城市现代化进程的快速发展，地下空间开发力度也随之加快，这使得新建盾构隧道近距离穿越或邻近既有盾构隧道的施工(近接施工)不可避免[1−6]。根据隧道之间空间位置关系，盾构隧道之间近接施工会出现相互交叉、双线平行和斜向并行等情况。许多学者针对盾构隧道之间相互交叉或双线平行进行了大量研究[7−12]，而在地铁设计时，为了避开周边建筑的影响，或者由于换乘功能需要，地铁线路会采用上下斜向并行(叠落)方式[13]。在双线盾构隧道修建过程中，当采用上下斜向平行方式时，控制后行盾构隧道施工所引起地层扰动对先行隧道的变形和附加内力的影响，对于确保先行隧道日后的正常运营以及后行盾构隧道本身的安全修建都具有重要意义[14]。孙钧等[15]运用ANSYS软件模拟了上海市轨道交通明珠线二期工程上、下行线近距离叠交区间隧道盾构施工过程，研究了盾构推进过程中土层位移与地表沉降的发展变化。陈先国等[16]依托深圳地铁1期工程罗湖至大剧院区间段，采用有限元法针对该工程的3 种典型上下并行重叠断面，按不同断面布局、不同开挖和支护形式进行了非线性分析计算。孙波等[17]以深圳地铁9号线银湖站西端五线叠落隧道为例，采用有限元数值模拟方法分析了不同情况下深圳6 号线与9 号线上下并行施工的相互影响。范晓真等[18]以杭州市环城北路地下通道为工程背景，通过有限元数值模拟方法，对小净距上下并行盾构隧道的施工扰动进行了研究。

综上所述，虽然在上下并行盾构隧道研究方面已取得不少成果，但目前大多数研究只是采用单一方法(数值模拟等)对上下并行隧道进行研究，很少有研究者结合不同手段深入分析上下斜向并行隧道中后行盾构隧道对先行盾构隧道的影响。为此，本文通过现场测试、数值模拟等方法，依托昆明地铁四号线小菜园—火车北站盾构隧道区间工程，研究富水圆砾地层近似平行叠落隧道上部后行盾构隧道施工对下部先行盾构隧道管片的位移、环向应力和弯矩的影响规律，以期为类似施工现场提供技术参考。

1 工程概况

1.1 区域地质概况

小菜园—火车北站隧道施工采用2台土压平衡盾构先后由右线和左线从小菜园始发，完成左右线隧道掘进任务后在火车北站解体吊出，左线隧道管片1 283 环，右线隧道管片1 277 环。本文研究的区段是从左线上部后行隧道第1 040 环到第1 090环，竖向对应右线下部先行隧道第1 035环到第1 085 环，目标管片为右线下部先行隧道的第1 060环管片(竖向对应左线的第1 065环管片)，左右线水平投影夹角为2.36°，基本呈平行状态。目标管片处左线上部后行隧道和右线下部先行隧道竖向净距为1.8 m，左右线隧道中心线距离为4.3 m，两隧道圆心连线偏离竖向28.26°，两者的目标管片处竖向相对空间位置如图1所示。

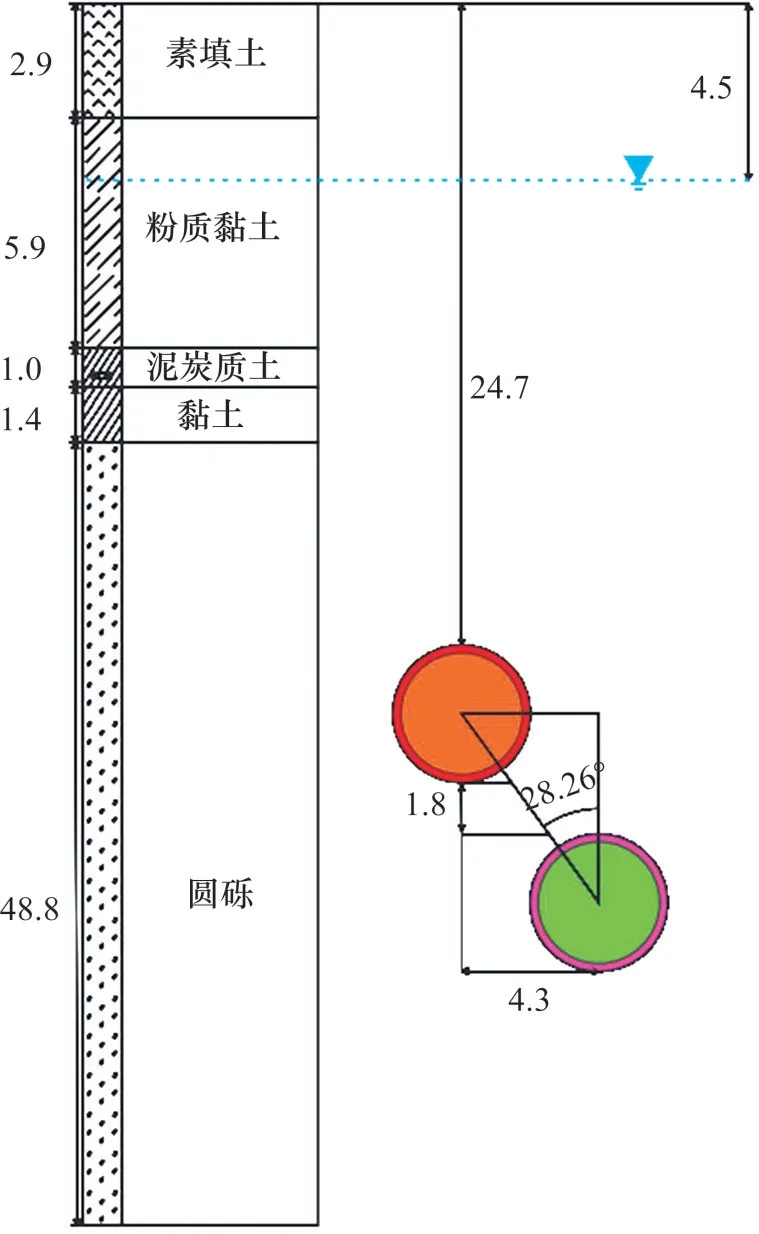
图1 目标管片处后行隧道和先行隧道竖向相对位置Fig.1 Vertical relative position of the later excavated tunnel and the former excavated tunnel at target segment

盾构穿越主要地层呈稍密—中密状，饱和，粒径以2～20 mm 为主，最大粒径为40 mm，砾石成分为砂岩、玄武岩等，颗粒磨圆度较高，以砂土充填为主，局部黏性土充填。经取样分析，粒径大于2 mm 的颗粒质量占总质量的64%～68%，粒径大于20 mm 的颗粒质量占总质量的13.78%。根据GB 50021—2001“岩土工程勘察规范(2009年版)”[19]，粒径大于2 mm的颗粒质量超过总质量的50%，土颗粒磨圆度较高的土属于圆砾，故可知盾构穿越主要地层为圆砾地层。小菜园—火车北站沿线地层主要包括素填土、黏土、粉质黏土、泥炭质土、粉土、粉砂、砾砂、圆砾，如图2所示。其中所研究区段自上而下主要为素填土、粉质黏土、泥炭质土、黏土、圆砾。各地层参数如表1所示。

图2 区段工程地质剖面Fig.2 Engineering geological section of shield section

表1 地层物理力学参数Table 1 Physical and mechanical parameters of formation

1.2 盾构施工参数概况

小菜园—火车北站区间采用厚度d为35 cm 的预制管片作为衬砌，拼装后外径D为6.2 m，内径φ为5.5 m。采用标准的6 分块，包括3 个标准块、2 个邻近块及1 个封顶块，错缝拼装，单环管片宽度h为1.2 m。管片间、管片环间都采用螺栓连接，管片材料为C50钢筋混凝土，抗渗等级为P12。

根据现场实测数据，左线盾构在所研究区段掘进过程中，推进速度基本保持在60 mm/min，总推力变化范围为14 000～20 500 kN，总推力平均值为183 37 kN，盾构刀盘扭矩在2 700～5 000 kN·m范围内波动。土仓上部压力变化曲线如图3所示。从图3可见：土仓上部压力在研究区段比较平稳，主要集中在0.19～0.25 MPa，平均值为0.22 MPa。

图3 土仓上部压力变化曲线Fig.3 Pressure change curve of the upper part of soil chamber

2 现场测试结果

2.1 现场测试方案

选取下部先行隧道(右线)第1 060环管片(对应于上部后行隧道(左线)第1 065 环)作为分析目标，研究上部后行隧道对其结构受力的影响。在管片内壁环向布置7个表面智能数码弦式应变计，利用综合测试仪采集数据。应变计性能参数如下：应变测量范围为±2 500με；应变测量精度为满量程的0.1%；应变分辨率为满量程的0.03%；测量标距为129 mm；使用环境温度为−40～80 ℃。应变计现场粘贴过程如下。

1)在管片表面用记号笔标记出打孔位置。使用钻机在标记位置上打直径为8 mm、深约30 mm的孔，清除孔内的碎屑。

2)按图4将应变计与安装座组装好，暂不拧紧螺钉。

图4 应变计安装示意图Fig.4 Schematic diagram of strain gauge installation

3)利用环氧树脂胶对应变计进行粘贴。粘贴时，A胶、B胶(质量比)按1:1混合搅匀(搅拌1 min以上)，然后将胶液灌入孔内。

4)将安装座圆柱插入灌胶后的孔内，需保证安装座圆柱完全插入后有胶溢出，若不溢出，则重新灌胶。

5)拧紧螺钉，用透明胶将应变计测试线贴在管片上。

在环氧树脂胶完全固化3 h后读取应变计的初始值，然后待上部后行隧道掘进到相应指定管片环数时，再读取应变计的测量值。此时，差值(即应变测量值与初值之差)为管片的附加应变，再根据管片的弹性模量可得管片附加应力。管片内壁应变计布点示意图如图5所示，按顺时针方向对应变计进行编号(1号至7号)。

图5 管片内壁应变计布点示意图Fig.5 Layout of strain gauges on the inner wall of segment

当上部后行盾构刀盘处推进到第1 040环时测取下部先行目标管片应变计和坐标点初始值，此时，上部后行盾构刀盘与目标管片水平距离(30 m)约等于管片外径的4.8倍。在上部后行盾构刀盘推进到第1 085 环时测取应变和坐标点最终值，此时，盾构刀盘与目标管片水平距离(24 m)约为管片外径的3.9 倍。通过2 次应变差值计算，可获取上部后行盾构掘进过程中目标管片环向附加应力。类似地，当上部后行盾构刀盘处已推进到左线第1 040 环时，利用全站仪测取目标管片各个测点处施工坐标，在盾构刀盘处推进到左线第1 085 环时，再测取1次施工坐标，以获取目标管片位置变化。应变计现场布置如图6所示。

图6 应变计现场布置Fig.6 Site layout of strain gauges

2.2 测试结果分析

利用所得施工坐标提取现场测量的盾构管片位移并进行分析，规定沿着盾构掘进方向水平向右为正。表2所示为上部后行盾构刀盘在第1 040～1 085 环之间的目标管片竖向位移和水平位移，可以看到管片左侧(测点1、测点2 和测点3，靠近上部后行左线隧道)测点处竖向位移总体大于管片右侧(测点5、测点6 和测点7，背离上部后行左线隧道)测点处竖向位移，表明上部后行盾构掘进对下部先行隧道目标管片靠近侧的影响相对于背离侧的影响较大。另外，拱顶处(测点4)管片水平位移最大，达3.9 mm。管片位置变化示意图如图7所示。在目标管片左右侧的竖向位移和水平位移差异效应下，目标管片沿顺时针发生了一定程度旋转。其原因是上部后行隧道开挖引起地层应力释放，导致下部隧道产生向上竖向位移，而靠近上部先行隧道侧的目标管片竖向位移要比背离侧的竖向位移大，故下部隧道表现为在整体上浮的同时也呈现一定的顺时针旋转态势。

表2 目标管片各个测点处竖向位移和水平位移Table 2 Vertical and horizontal displacements at each measuring point of target segment mm

图7 管片位置变化示意图Fig.7 Schematic diagram of segment position changes

环向附加应力指的是管片相对于现场测试应力初值的变化值，其中正号表示附加拉应力，负号表示附加压应力。下部先行隧道目标管片测点1至测点7 处环向附加应力分别为0.9，0.2，−0.8，0.8，0.7，0.2和0.1 MPa，可见测点2、测点6和测点7 内壁环向附加应力接近于0 MPa，而测点1、测点4 和测点5 内壁受到的环向附加应力相对较大，这些测点处应力都表现为附加拉应力，仅测点3 环向应力表现为附加压应力(−0.8 MPa)。其原因是在上部后行隧道开挖作用下，下部先行右线目标管片左上角的地层应力释放，产生类似“斜上拉力F”的荷载(见图8)，而右下角地层背离后行隧道，地层应力变化有限，在左下角和右上角斜向地层压力作用下，导致目标管片左上角的外壁“凸出”，内壁呈现为附加压应力。沿着向上方向，管片右侧测点处(测点7、测点6和测点5)环向附加应力呈递增趋势，管片左侧测点处(测点1、测点2和测点3)环向附加应力也呈递增趋势。总体来看，在上部后行隧道开挖引起的地层应力释放作用下，靠近上部隧道测点处环向附加应力沿竖向变化的幅度较大，即上部后行隧道开挖会引起近侧管片环向应力变化梯度比远侧的更大。

图8 目标管片外力变化示意图Fig.8 Schematic diagram of external force changes of target segment

3 数值模拟及结果分析

3.1 数值建模

3.1.1 数值模型

由于现场测试数据有限，为了深入探究上部后行盾构掘进对下部先行盾构隧道目标管片内力的影响，以盾构刀盘到达位置所在环数为坐标横轴，采用Flac3D 对掘进过程进行数值模拟，上部后行盾构掘进实际环数1 040～1 090 环对应的数值模拟环数为0～50环。

数值模型如图9所示。模型沿着隧道横向取60 m，沿隧道纵向取60 m，高度取50 m。模型中的岩土体采用实体单元进行模拟，盾构隧道中的管片采用shell 单元进行模拟。设置模型边界条件如下：前后及两侧约束水平位移，底面边界约束水平和竖向位移，模型上边界地表为自由边界。整个模型网格划分共剖分72 675个节点，68 100个单元。

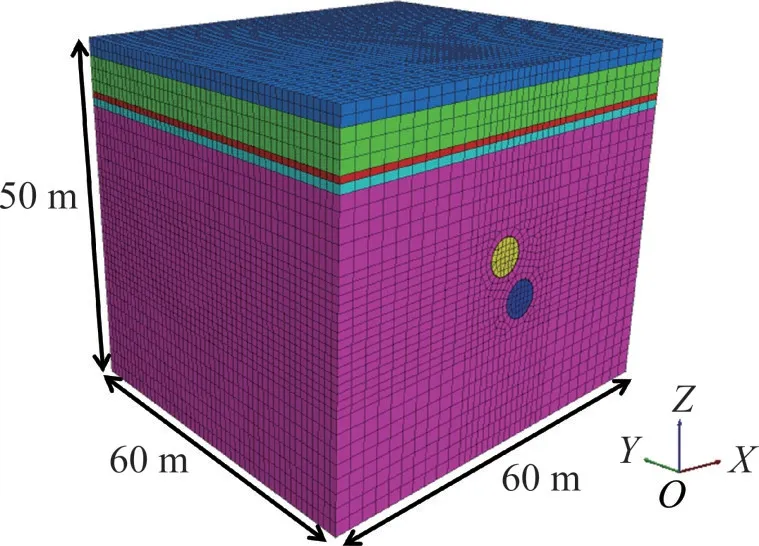
图9 数值模型Fig.9 Numerical model

盾构掘进模拟示意图如图10所示。该模型盾构掘进方向总长为60 m，每步长为1.2 m(等于管片宽度)，共分为50步进行开挖和支护。

图10 盾构掘进模拟示意图Fig.10 Schematic diagram of shield tunneling simulation

3.1.2 模型力学参数

考虑到盾构掘进过程中地层来不及排水，数值模型中土层采取不固结不排水试验强度参数[20](见表1)，而涉及的结构单元计算参数如表3所示。计算主要基于以下假设：

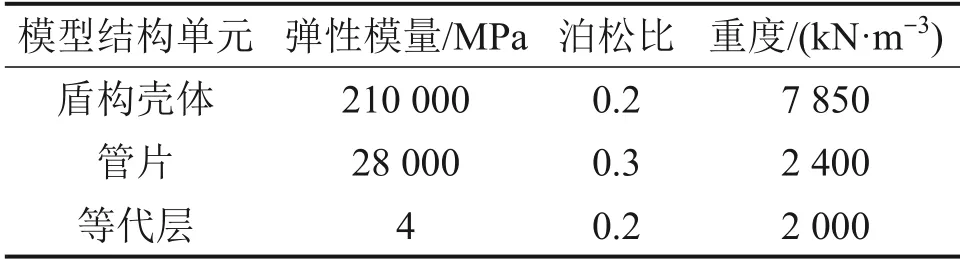
表3 模型结构单元计算参数Table 3 Calculation parameters of model structural unit

1)计算中盾构衬砌管片引入刚度折减系数0.8以模拟环间接缝效应[21−22]。

2)土层材料采用Mohr−Coulomb 模型进行模拟，管片、盾壳等结构材料采用弹性模型进行模拟。

3)基于盾构掘进参数记录，在数值模拟过程中土仓上部支护压力保持在0.22 MPa，向下以15.6 kPa/m 梯度递增，注浆压力保持在0.35 MPa。将衬砌管片壁后受扰动土体和注浆情况概化为均质等厚的等代层进行计算。

3.1.3 现场验证

为了验证数值模拟的正确性，将上部后行盾构刀盘从1 040 环(对应数值模拟第0 环)与第1 085环(对应数值模拟第45环)之间的竖向位移和环向附加应力变化值的数值模拟结果与现场测试结果进行对比，如图11和图12所示。从图11和图12可见：竖向位移和环向附加应力变化值的数值模拟结果与现场测试结果吻合良好，说明数值模拟方案基本反映了实际情况，同时，证明了测试结果所反映的上部后行盾构在掘进过程中目标管片发生了一定程度的顺时针旋转且受到类似一种“斜向拉力”的作用。

图11 数值模拟与现场实测位移对比Fig.11 Comparison of displacement between numerical simulation and field measurement

图12 数值模拟与现场实测环向附加应力对比Fig.12 Comparison of additional hoop stress between numerical simulation and field measurement

4 讨论

4.1 下部先行隧道目标管片位移变化规律

图13所示为上部后行盾构掘进过程中下部先行隧道目标管片的竖向位移变化规律，以目标管片竖向对应的上部隧道管片位置为水平距离起始计算点，规定上部隧道刀盘到达目标管片正上方位置前的水平距离为负，远离目标管片时水平距离为正，并将刀盘距离目标管片的水平距离L换算成盾构管片外径D的倍数。

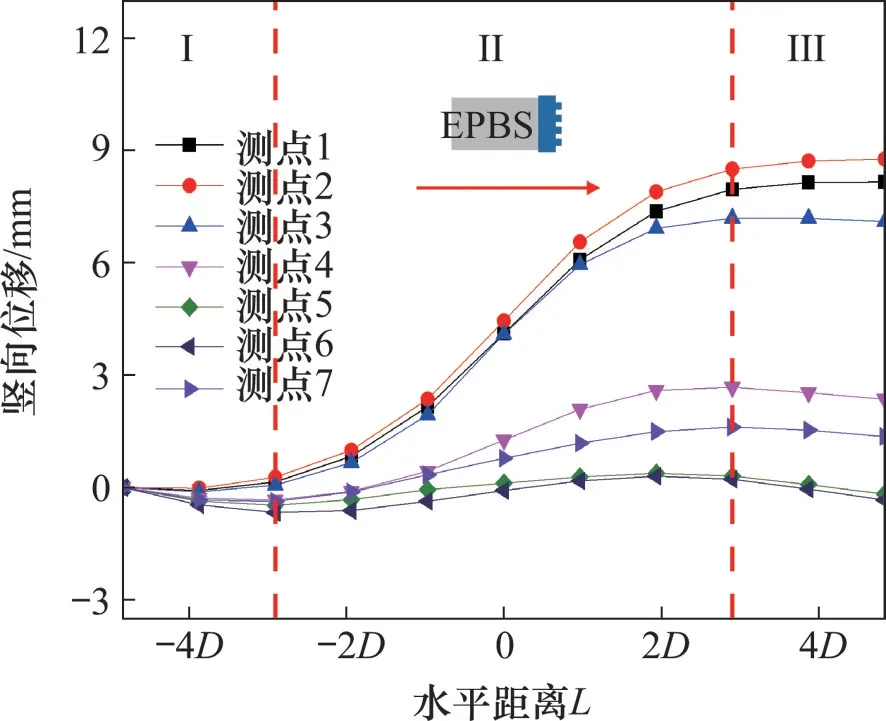
图13 上部后行盾构掘进中目标管片竖向位移变化Fig.13 Upright displacement change of target segment during the later excavated upper shield tunneling

靠近上部后行隧道侧的目标管片测点1、测点2 和测点3 的竖向位移随水平距离变化过程趋势总体是相同的，背离上部后行隧道侧的目标管片测点5、测点6 和测点7 的竖向位移变化趋势总体上相同，各个测点处竖向位移变化过程大致可分为缓慢变化(Ⅰ)阶段、快速增长(Ⅱ)阶段和趋于平稳(Ⅲ)阶段。

在缓慢变化阶段(Ⅰ)，L为−4.8D～−2.9D。由于上部后行盾构刀盘距目标管片还较远，对地层产生的应力干扰还未影响到目标管片，所以，上部后行盾构掘进引起测点1、测点2 和测点3 竖向位移变化缓慢。类似地，背离侧目标管片测点5、测点6和测点7的竖向位移变化也较缓慢。

当进入快速增长阶段(Ⅱ)即L为−2.9D～2.9D时，随着刀盘不断靠近目标管片上方地层，应力扰动开始对目标管片产生较大影响，所以，测点1至测点7 竖向位移快速增大，且在L=0D时管片竖向位移增长最快。其中靠近上部后行隧道的目标管片测点1、测点2 和测点3 处竖向位移变化趋势较接近，但竖向位移变化差异开始显现。背离上部后行隧道的目标管片测点5、测点6 和测点7 处竖向位移变化趋势较接近，但竖向位移变化也开始呈现出差异。这说明只有在该阶段，靠近上部后行隧道侧与背离上部后行隧道侧之间因为上部后行盾构掘进产生的位移差才足以使目标管片产生旋转态势。

趋于平稳阶段(Ⅲ)即L>2.9D时，管片各个测点处位移已基本不再变化，测点1至测点7处竖向位移分别达到8.16，8.78，7.12，2.36，−0.18，−0.34和1.36 mm。

上部后行盾构掘进到不同环数时目标管片位置变化示意图如图14所示。其中，坐标只针对管片位置变化，并不表示管片的实际尺寸。以下部先行隧道开挖后上部后行盾构还未掘进之前作为目标管片的初始位置，正号表示管片位置向初始位置外侧变化，负号表示管片位置向初始位置内侧变化，测点1'至测点7'表示7个位置变化监测点。从图14可见：在盾构掘进到10环时，目标管片位置基本没有变化，此时，正好对应管片位移变化第Ⅰ阶段的结束；在盾构掘进到20环时，目标管片位置已发生轻微变化，尤其在靠近上部后行隧道侧较明显，这一阶段刚好对应管片位移变化第Ⅱ阶段的起始段；在盾构掘进到30 环时，目标管片位置发生了明显变化，且位置变化集中体现在靠近上部后行隧道侧，目标管片按顺时针旋转了一定角度，这与管片位移变化第Ⅱ阶段的中间段变化规律是一致的；在盾构掘进到40 环时，目标管片位置较掘进到30 环时仍有少量变化，表明管片位置变化已达到第Ⅱ阶段的末尾段；在盾构掘进到50环时，目标管片位置较盾构掘进到40 环时几乎没有变化，这与管片位移第Ⅲ阶段所反映的管片位移变化特征是相同的。

图14 上部后行盾构掘进到不同环数时目标管片位置变化示意图Fig.14 Schematic diagram of position of target segment during later excavated upper shield tunnels to different number of rings

4.2 下部先行隧道目标管片环向应力变化规律

上部后行盾构掘进过程中目标管片环向应力变化如图15所示。从图15可见：不同于目标管片各个测点处的竖向位移变化值，管片内壁各个测点处的环向应力变化趋势都不尽相同。随着盾构刀盘不断接近目标管片，在水平距离L为0D时，各个测点环向应力变化幅度较大。其中，在上部后行盾构掘进过程中，目标管片4号测点处一直承受环向拉应力，最大值可达2.00 MPa左右，3号测点处一直承受环向压应力，且最大值约−1.52 MPa。

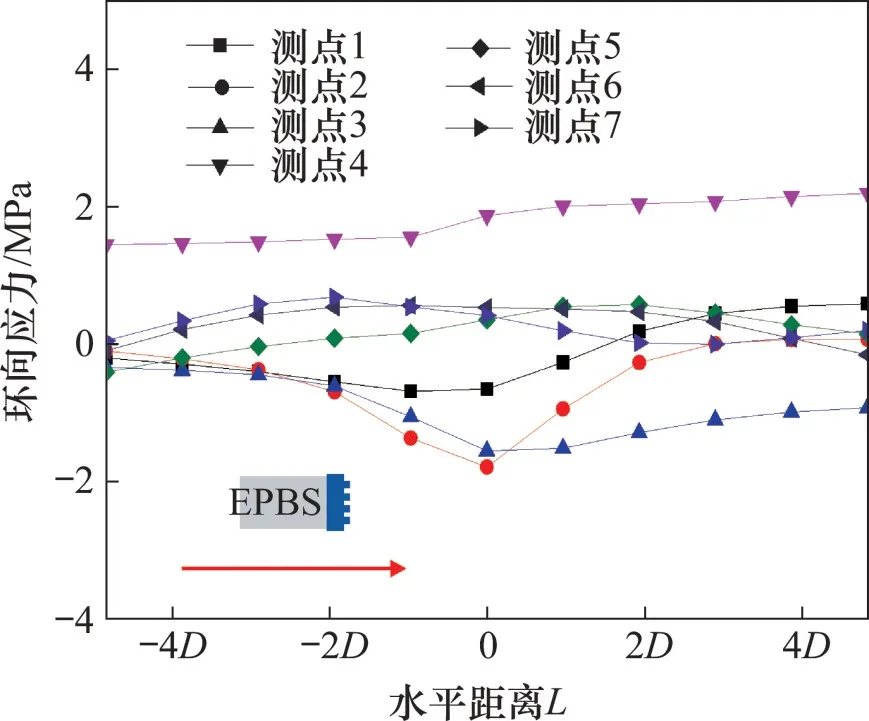
图15 上部后行盾构掘进过程中目标管片环向应力变化Fig.15 Hoop stress change of target segment during later excavated upper shield tunneling tunneling

为了更好地体现出上部后行盾构在掘进过程中目标管片内壁所受环向应力变化规律，绘制上部后行隧道掘进到不同环数时目标管片内壁所受环向应力分布示意图，如图16所示(规定拉应力为正，压应力为负)。从图16可见：在后行盾构隧道掘进之前，先行隧道目标管片在受到土体自重应力和土体开挖引起的应力扰动影响后，内壁所受环向应力基本呈“蝴蝶”状左右对称分布，拱腰内壁两侧受轻微的环向压应力，拱顶内壁受较大的环向拉应力，达1.45 MPa；在盾构掘进到10 环时，“蝴蝶”左翼向隧道外侧扩张，右翼向内侧收缩，目标管片内壁拱腰左侧所受压应力继续增大，拱腰右侧开始承受环向拉应力，拱顶和拱底处所受环向应力变化不大；在盾构掘进到20环时，“蝴蝶”左翼向隧道外侧进一步扩张，拱腰左侧环向压应力达到整个掘进过程最大值(−1.37 MPa)，右翼环向压应力基本保持不变，此时“蝴蝶”已明显呈不对称分布；在盾构掘进到30 环时，“蝴蝶”左翼总体向隧道内侧收缩，但收缩扩张幅度不大，右翼变化不明显，拱顶处所受环向拉应力达到2 MPa 左右，且增幅较大，较掘进20 环时增加0.45 MPa；在盾构掘进到40环时，“蝴蝶”左翼向隧道内侧收缩，右翼较掘进到30 环时环向拉应力变化不大；在盾构掘进到50环时，“蝴蝶”形状与掘进40 环时相比已基本保持不变，反映出目标管片所受应力已趋于稳定。

图16 上部后行盾构掘进过程中目标管片环向应力分布Fig.16 Hoop stress distribution of target segment of during later excavated upper shield tunneling

为了更好地反映目标管片测点处环向应力在上部后行盾构掘进过程中的变化过程，将上部后行隧道开挖前应力清零，绘制出目标管片测点处环向附加应力随上部后行盾构掘进变化过程图，如图17所示。

从图17可以看到，根据环向附加应力变化情况可将目标管片测点处环向附加应力随上部后行盾构掘进变化过程分为3个阶段。

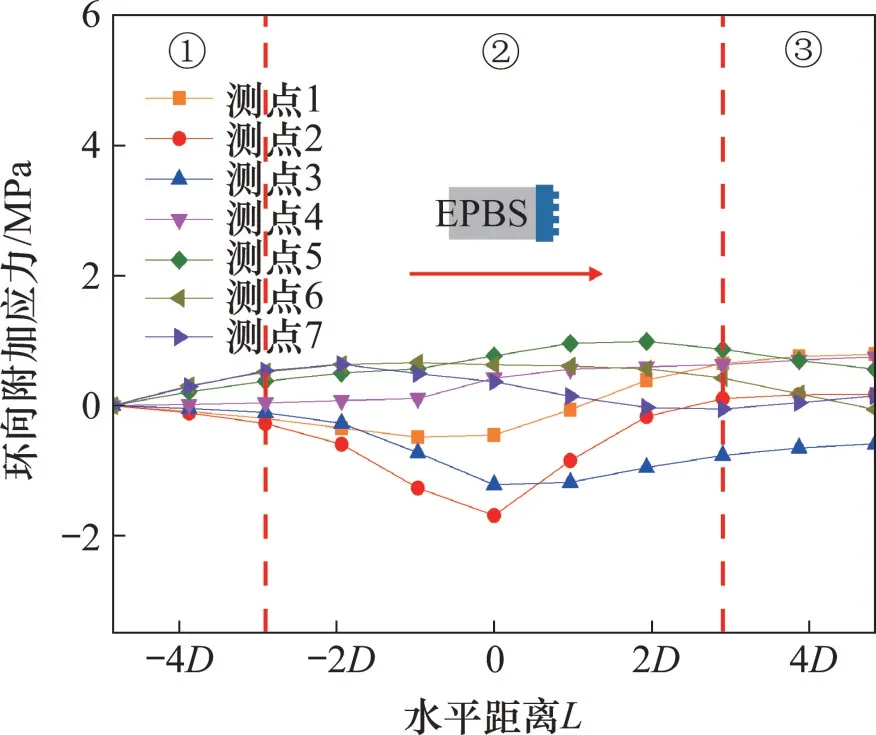
图17 上部后行盾构掘进过程中目标管片环向附加应力变化Fig.17 Additional hoop stress change of target segment during later excavated upper shield tunneling tunneling

①阶段，L为−4.8D～−2.9D，测点1、测点2和测点3处环向附加应力变化接近，且变化缓慢，测点5、测点6 和测点7 处环向附加应力变化趋势一致。总体上，测点1至测点7处环向附加应力变化缓慢。

②阶段，L为−2.9D～2.9D，测点1～测点7处环向附加应力变化剧烈且程度不一，说明此阶段目标管片内侧各处受到了不同程度的挤压拉伸。

③阶段，L>2.9D，目标管片内壁各处环向附加应力变化已基本趋于稳定，可以看到测点1、测点2和测点3处环向附加应力仍小幅度减小，测点4、测点5、测点6和测点7处环向附加应力小幅度增加，这主要是靠近目标管片处的盾尾处施加的注浆压力引起的。

4.3 上部后行盾构掘进过程中既有隧道目标管片弯矩变化规律

地铁隧道管片衬砌的弯矩是管片受力状态的1个重要指标，可以根据管片的弯矩变化判断管片的压弯程度，这也是进行管片设计配筋的主要依据[23]。上部后行盾构掘进到不同环数时目标管片弯矩分布如图18所示。从图18可以看到：在整个上部后行盾构掘进过程中，目标管片拱顶和拱底均承受较大正弯矩，左右两侧则承受较大负弯矩。

图18 上部后行盾构掘进到不同环数时目标管片弯矩分布Fig.18 Additional hoop stress change of target segment during later excavated upper shield tunneling

通过进一步分析可知，上部后行盾构在掘进之前，由于初始地应力作用以及右线本身开挖后应力重分布影响，目标管片所受弯矩呈“∞”形对称分布，其中，拱顶、拱底、左拱脚和右拱脚所受弯矩分别为257.1，229.4，−255.1和−245.9 kN·m；盾构在掘进到10 环时，拱底弯矩分布基本不变；盾构在掘进到20 环时，拱脚左侧弯矩已有轻微增加，拱脚右侧弯矩基本没有变化；盾构在掘进到30 环时，弯矩明显呈现非对称分布，且两侧最大弯矩向左右线隧道中心连线发生顺时针偏转，其中隧道A 处增幅最大，该处弯矩增加幅值较掘进20 环时达到117.0 kN·m。此时，管片所受最大正弯矩达到349.5 kN·m，较掘进20 环时增加约20.0%，最大负弯矩达到−311.2 kN·m，较掘进20环时增加约8.4%；盾构在掘进到40 环时，弯矩较掘进30 环时仍有较小幅度增加，最大正弯矩为372.7 kN·m，最大负弯矩达−330.9 kN·m；盾构在掘进到50 环时，弯矩分布形状已基本没有变化，这表明管片所受弯矩状态已趋于稳定。

由于整个上部后行盾构掘进过程中目标管片拱顶和拱底承受较大正弯矩，两侧拱脚部位承受较大负弯矩，故拱顶、拱底和两侧拱脚处所受弯矩可以很好地反映管片安全性能状态。绘制上部后行盾构掘进过程中目标管片拱顶、拱底和两侧拱脚处所受弯矩变化曲线，如图19所示。

从图19可以看到：拱顶所受弯矩总体上大于拱底所受弯矩，而两侧拱脚弯矩差距不大；在整个上部后行盾构掘进过程中，目标管片拱顶、拱底和两侧拱脚处承受的弯矩一直增大，但总体增长幅度不大；当L>2.9D时，目标管片所承受弯矩基本无变化；当L为−0.97D～0.97D时，弯矩变化较明显。

图19 上部后行盾构掘进过程中目标管片最大弯矩值变化Fig.19 Change of maximum bending moment of target segment during later excavated upper shield tunneling

5 结论

1)富水圆砾地层上部后行隧道盾构掘进引起靠近后行线侧目标管片的位移大于背离侧的位移，目标管片在这一过程中发生了一定程度的顺时针旋转，且在后行隧道开挖引起地层应力释放下，在两隧道中心连线方向上存在对先行管片类似“斜向拉力”的外部荷载作用。管片竖向位移变化过程大致可分为缓慢变化(Ⅰ)、快速增长(Ⅱ)和趋于平稳(Ⅲ)3 个阶段，其中，在L=0D时，管片竖向位移增长最快，在施工阶段应引起注意。

2)上部后行隧道在盾构掘进过程中，管片内壁拱顶处一直承受环向拉应力，且最大值可达2 MPa左右。上部后行盾构在掘进时，目标管片测点处环向附加应力变化阶段与竖向位移变化阶段在宏观上是一致的。当L为−2.9D～2.9D时，在这段掘进过程中，目标管片承受环向附加应力变化较剧烈且程度不一。

3)下部先行隧道管片拱顶、拱底以及两侧拱脚部位均承受较大弯矩，然而，在上部后行盾构掘进过程中，下部先行隧道目标管片弯矩的变化程度较竖向位移和环向应力低，整个掘进过程对地层所产生的应力扰动并不会显著改变目标管片所受弯矩状态，仅当L为−0.97D～0.97D时，弯矩变化略明显。

4)在上部后行隧道掘进过程中，下部先行右线目标管片左上角的地层应力释放会引起类似“斜上拉力F”的荷载。为确保在上部后行盾构掘进过程中下部先行成型隧道的结构安全，对于富水圆砾地层斜向并行隧道，建议对上部后行和下部先行盾构隧道之间的地层从先行隧道洞内深孔注浆，以降低后行盾构掘进对该地层的扰动和先行洞的变形。