透过题干抓本质 类比推理巧解题

白银市第一中学

高晓艺

1 问题提出

类比推理也称类比法.在人教A版选修1-2中第二章推理与证明中有系统详细的介绍.类比推理是培养和提升学生逻辑推理素养的重要的知识载体.而在教学过程中，我们发现学生在应用类比推理解题时往往存在思维过程无法落地的困惑.仅仅追求所得结论与题干已知结论的“形似”，而忽略了类比的本质“神似”.从而导致了对一些较为复杂的问题无从下手求解.

实际上，在进行类比推理时，我们所需要的核心并不是结论的一致性或者相似性，而是透过现象看本质，挖掘在解题过程中对本质思想或方法的类比过程.

本文中将结合几个利用类比推理思想来求解的具体案例进行实践和反思.

2 教学案例

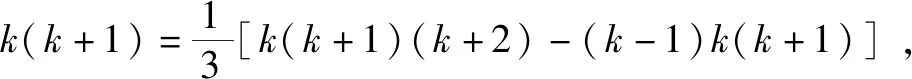
请你类比上述方法，计算1×2×3+2×3×4+……+n(n+1)(n+2)的结果.

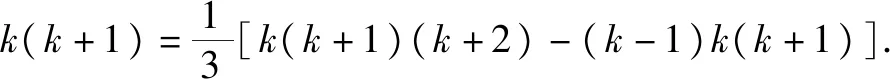
解：依题意可得

由此可得

…………

以上n个式子相加，得

问题推广1：

“计算1×2×3×4+2×3×4×5+……+n(n+1)(n+2)(n+3)的值.”[1]

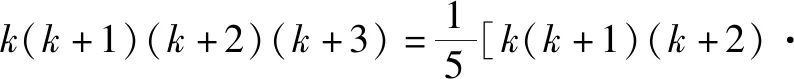
问题推广2：

求12+22+32+……+n2的值.

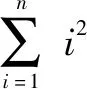
=1×2+2×3+……+n(n+1)-(1+2+……+n)

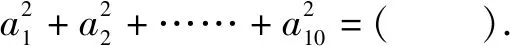
A.714 B.1870 C.4895 D.4896

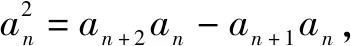
解：由an+1=an+2-an，得

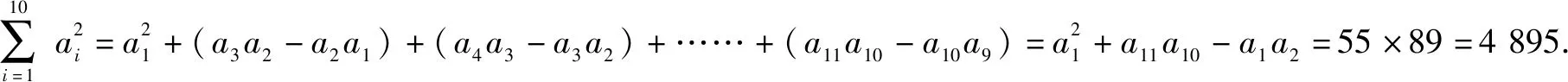
例3在等差数列{an}中，若a10=0，则有a1+a2+……+an=a1+a2+……+a19-n(n<19,且n∈N*)成立.类比上述性质，在等比数列{bn}中，若b9=1，则存在怎样的等式？

分析：等差数列与等比数列由于具有相似的定义和性质而经常进行类比.首先分析题干本质，在等差数列中,由a10=0,易知，an+a20-n=0,即an+1+a19-n=0，故an+1+an+2+……+a19-n=0，因此有结论a1+a2+……+an=a1+a2+……+a19-n成立.那么类比到等比数列中，由b9=1，得bn·b18-n=1，即bn+1·b17-n=1，因此bn+1·bn+2……b17-n=1，故可类比推理得出相应的性质b1·b2……bn=b1·b2……b18-n(n<18，且n∈N*).

解：在等比数列{bn}中，若b9=1，则有b1·b2……bn=b1·b2……b18-n(n<18，且n∈N*).

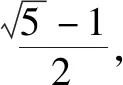
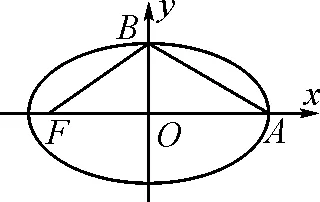
图1

分析：首先分析题干中“黄金椭圆”的离心率求解过程，进而类比求解“黄金双曲线”的离心率.其实质依然是求解过程及思路的类比，是思想方法的迁移.

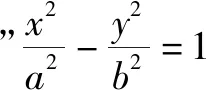
3 教学反思

开普勒曾经说过：“我珍视类比胜过任何别的东西，它是我最可信赖的老师，它能揭示自然界的秘密.”的确，我们经常应用平面几何的结论去类比推理得到空间几何中的一些结论，也会不断地将等比数列与等差数列进行类比学习.在教学过程中，我们也经常应用类比已有知识的形成过程去习得新知.比如，在学习“数学归纳法”这一内容时，就会类比多米诺骨牌游戏的原理，从而容易理解数学归纳法的证明原理.类比推理为我们获得新知识和新结论提供了方向和思路，也是我们解题中不可或缺的好帮手.在日常教学过程中，教师应该重视对学生类比推理思维的培养.这个培养不是通过一道题或者一堂课就能做到的，而应该是一个不断渗透，慢慢形成的过程.教师在具体的解题教学过程中，应该重视对类比过程的分析和引导，鼓励学生抓住问题的本质去进行类比，尤其是在思想方法的类比过程中，应该重视举一反三，重视变式练习和对问题的推广应用.只有在由易到难不断应用的过程中，才能逐渐培养和提升学生的逻辑推理素养.