磁流变测量系统的控制滞后与动态响应

吕靖成 危银涛 邬明宇 何俊祥 梁冠群 尹 航

清华大学车辆与运载学院，北京，100084

0 引言

磁流变液(magnetorheological fluid，MRF)由RABINOW[1]于1948年发现，是一种黏度可受外加磁场调控的智能材料。因具有响应快和黏度变化大等优异性能，MRF成为连接机械系统和电控系统的优质材料。目前发展出的应用如下：力矩传递[1-3]、抑制振动[4-5]、形成压力降[6]、密封[7]和抛光[8]等。将MRF及其所连接的机械系统和电控系统的集合体称为磁流变系统(magnetorheological system，MRS)。

高性能的磁流变系统不仅需要可调力值范围大[9]，还需要拥有优良的控制策略[10]，即要在恰当时机给设备合适的激励。然而，该机械电子系统中的控制信号经电路产生电流，再经磁路产生磁场，最后磁流变液响应，其中每个环节都有一定的滞后，并最终导致控制时机的偏差。YOON等[11]与QIN等[12]的研究都表明，时间滞后对较高频率下的控制效果有着极大的影响。故而，系统时滞的减少与系统动态响应特性的良好建模对磁流变减振器系统十分重要。

由于磁流变系统滞后特性研究的多学科交叉特性以及该系统的非线性特性使得建模研究困难，因此目前此类研究还未受到学术界的广泛关注。同时，对MRS动态特性的研究也多集中于单纯的机械系统受外界激励的响应[13]。MRS受控制信号激励响应特性的实验研究主要通过施加阶跃激励观察响应的滞后情况并对其进行简单分析，且未将各部分的滞后响应行为分离研究[14-15]，而对该特性的理论研究也多缺乏实验结果的支持[16]。

对MRS各部分进行分析，可知其受控制信号激励时的响应滞后。在电路中，由于感抗的存在，电流的相位会滞后于电压。在磁路中，也存在类似的磁滞效应，表现为磁滞损失和涡流损失。根据磁路转化原理以及电磁感应定律，磁流变设备的磁路可转化为L-R等效电路，并可与电路串联进行分析和测量。而在动态磁场条件下，可逆磁导率随磁场强度变化[17]，该蝶形滞回曲线同样可以视为某种形式的滞后，且与频率和偏置等诸多因素相关[18]。磁流变液通常被认为在外加磁场条件下性质可逆且瞬间发生改变，然而事实上它也会在剪切应变和外加磁场的激励下出现滞后[15]。这部分滞后的出现主要是因为磁流变液中的磁性颗粒在时变的外加磁场条件作用下的聚集和解离需要时间。

总而言之，了解MRS受控制信号激励的动态响应特性对提高其性能很重要，但目前学界对此的认识和研究都相对欠缺，考察内容也不够全面，忽略了很多潜在的重要特性，与无级控制的MRS实际工况相去甚远。因此，本文提出一套用于研究MRS动态特性的测试系统，并对系统随偏置、振幅和频率变化的动态行为进行研究。在MRS设备的实际应用中，电路中的电流仍能够通过回采获得，但却不会再对磁感应强度和MRF特性进行测量，因此本文主要针对电流和剪切应力间的重要环节(即磁场滞后和MRF滞后)进行更加细致的分析与仿真。

1 系统滞后分析

1.1 理论模型

如前所述，磁路中存在磁滞效应，表现为磁滞损失和涡流损失。在不考虑B-H曲线动态响应的情况下，圆筒磁芯的涡流损失为[16]

(1)

令通过磁芯的磁通量

φ(t)=AB(t)=A(Bmsin(ωt)+B0)

得

(2)

式中，ρ为电阻率；R为外径；r为内径；h为高度；A为面积；Bm为磁感应强度交流部分的幅值；B0为磁感应强度的偏置部分；f为激励磁场的频率；ω为激励磁场的角频率，与激励电流的角频率相同。

由此可知，磁芯的涡流损失与磁芯材料的电阻率成反比，与磁芯高度成正比，与交流磁场幅值的平方成正比，与交流磁场频率的平方成正比，还与磁芯结构有关。

磁路的磁滞损失(图1)则与磁芯材料、磁感应强度波动的幅值、磁场频率和磁芯体积有关，常用的简化公式[19]为

图1 可逆磁导率随直流磁场变化曲线Fig.1 The change curve of reversible permeability with magnetic field

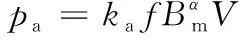
(3)

式中，ka为与磁芯材料特性有关的系数，磁滞回路的面积越小，ka越小；V为铁芯的体积；α为控制系数，由Bm确定，Bm<1.0 T时，α=1.6。

图1中，μrev为可逆磁导率，μi为起始磁导率，μr为剩磁磁导率。

由于电磁感应，故磁路滞后与由电感导致的电路滞后相互关联。根据磁路转化原理，MRS的磁路可转化为L-R等效电路，将其与系统电路串联，如图2所示。等效电路部分的响应表达式为

图2 磁流变测试设备简化视图Fig.2 Illustration of the magnetorheological system

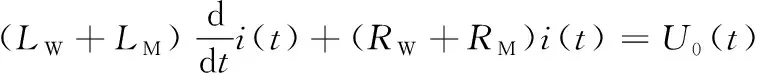
(4)

式中，LW为线圈电感；RW为电路电阻；LM为磁芯的等效电感；RM为磁芯的等效电阻；U0(t) 为电源电压；i(t)为电路中的电流。

在简化条件下，RW和LM可以认为是常数[20]，RM和LW则为

(5)

(6)

式中，N为线圈匝数；K为磁芯的结构参数。

由于式(5)和式(6)中含有电流项，使得式(4)成为一阶非线性的微分方程，无法得到解析解，故将式(5)和式(6)中的电流项用有效值代替，RM和LW变为常数项，将式(4)简化为一阶线性微分方程，其解为

(7)

电路中的电流i(t)可以通过电流表回采至计算机中，磁芯中的磁场强度随绕组中的电流同步变化，即

(8)

式中，l为磁路的长度。

在忽略漏磁的情况下，磁芯中的磁感应强度应与磁流变液中的一致，其值为

B(t)=μ0μr(t)H(t)

(9)

式中，μ0为真空磁导率，μ0=4π×10-7H/m；μr(t)为相对磁导率，其值会随磁场强度偏置和振幅以及交变频率变化而变化[18]，产生磁场滞后。

1.2 实验

综上所述，系统滞后的主要组成部分有：等效电路滞后(电源U0(t)与电流i(t)间)、磁场滞后(磁场强度H(t)与磁感应强度B(t)间)和磁流变液滞后(图3，磁感应强度B(t)与剪切应力τ(t)间)，本文不考虑剪切应变γ(t)和剪切应力τ(t)间的滞后。

图3 磁流变液的交变响应Fig.3 Response of magnetorheological fluid to alternating magnetic field

针对上述情况，本文提出了系统滞后的测量方案(图2)。电源信号由程序控制，近似认为不存在滞后；电路中的电流可以通过电流计回采得到；磁感应强度可由置于测试平台底座的高斯计测得；而屈服应力可由流变仪测得。如此，便可分别对系统滞后的各部分特性进行研究。

本文使用安东帕的MCR702流变仪进行研究，使用查表法生成直流加交流的电流，固定剪切速率进行测试(设定每次测试的循环次数为10)。在正式测试前，设置模块在偏置电流和固定的剪切速率下进行预剪切，保证正式测试中不会因为电流和剪切速率的突变而引入滞后或扰动。磁流变液由体积占比为30%的巴斯夫CIP SQ球形铁粉(D50为3.9～5.0 μm)和基载液混合制得。

2 实验结果与分析

首先，对通常的电流测试范围进行准静态的扫描测试，获得τ-I的循环测试曲线，如图5所示，并将该曲线作为后续动态测试分析的基础。在准静态测试中，电流与电感强度一一对应。不难发现该循环测试曲线中仅在中等电流大小时存在极小的滞回区，且在0 A和±5 A处收敛为点。

图4 磁流变设备的静态响应Fig.4 Static response of the magnetorheological system

(a)无偏置

(b)2A偏置图5 磁流变设备的动态响应Fig.5 Dynamic response of the magnetorheological system

设定0 A处的剪切应力为零，对该曲线分别进行线性和非线性拟合，可得

τ=35739Bsgn(B)

(10)

τ=2.756×104sin2(1.987B)

(11)

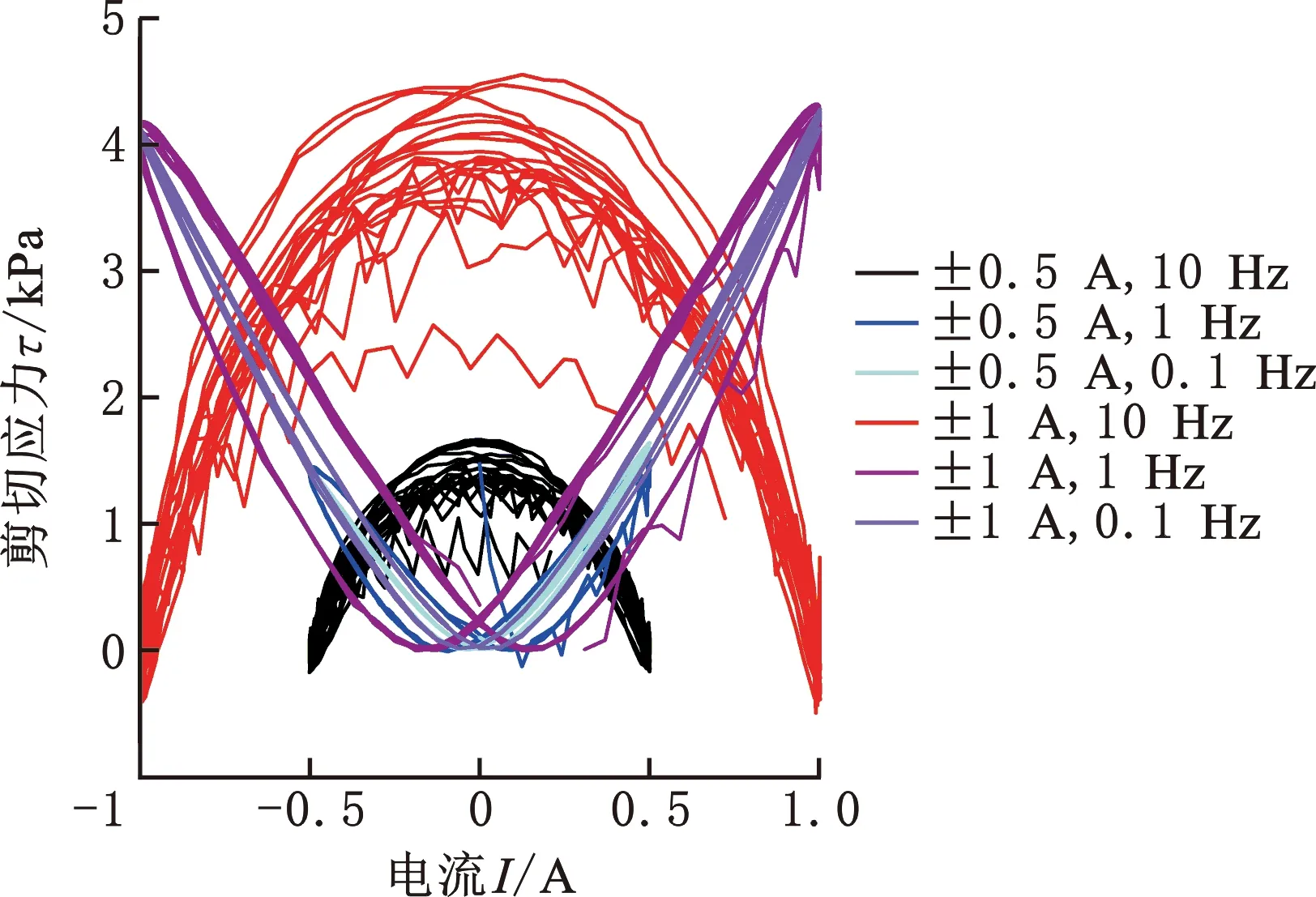
在无偏置和2 A偏置条件下，进行变频(0.1，1，10 Hz)和变振幅(0.5，1 A)的实验，并绘制其τ-I曲线，如图5所示(共10次循环)。由图5不难发现振幅的变化主要影响τ-I曲线的尺寸，而激励频率则会显著改变曲线的形状。由图5a知，0.1 Hz下曲线就出现分叉，即存在两个极小值点；而随着激励频率增至1 Hz，曲线的滞后环面积增大，两个极小值点进一步远离0 A；而当频率为10 Hz时，曲线突然变为开口向下的抛物线形状，并出现了电流增大、磁流变液剪切应力值反而下降的奇怪现象。由图5b知，低频激励的I-τ曲线滞回较小，而随激励频率增加，滞后环的面积也逐渐增大。

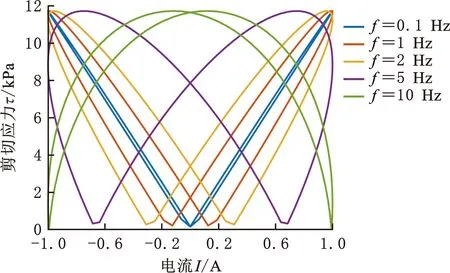
针对无偏置条件测得τ-I曲线的异常现象，固定振幅为1 A，进一步细化激励频率，结果如图6所示(10次循环)。出现非常明显的蝶形曲线，在0 A处两侧曲线相交于一点，且该点的纵坐标随频率逐渐增大；蝶形曲线的下沿，即两个极小值点，则逐渐向两侧移动，并在10 Hz时到达±1 A位置；滞回曲线的面积则随着频率的增加先增大后减小。此外，经数据分析知，该系统无法产生10 Hz以上的交流电，相关数据不可信，故在此略去。

图6 无偏置的动态频率响应Fig.6 Unbiased dynamic frequency response

推断上述τ-I曲线随激励频率发生变化主要源于迟滞现象，因此对其滞后相角进行分析。方法是利用傅里叶拟合I-t和τ-t曲线，形式如下：

i(t)=A′sin(ωt-φ0)+ibias

(12)

τ(t)=A″sin(ωt-φ0-φ)+τbias

(13)

式中，ibias、τbias分别为电流和剪切应力的偏置量；A′、A″分别为电流和剪切应力正弦部分的振幅；φ0为U0(t)与i(t)间的滞后相角；φ为i(t)与τ(t)间的滞后相角。

处理后即可得U0(t)与i(t)以及i(t)与τ(t)间滞后相角随激励频率的变化曲线，如图7所示(2 A偏置，0.5 A振幅)。不难发现，U0(t)与i(t)间的滞后相角随激励频率的增大最初快速增大，而后变化速度逐渐变慢(图7a)。

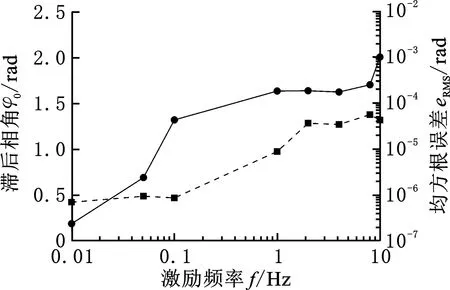
(a)U0(t)与i(t)间

由于电磁部分的动态响应特性并非本研究关注的核心，故对图7a不做过多讨论。HANS等[21]通过测量该子系统的动态响应得出其特征时长约为50 ms，即前文所述响应时间为150 ms。而i(t)与τ(t)间滞后相角则基本随激励频率线性增加(图7b)，用过零点的线性方程拟合可得

φ=0.145 16f

(14)

若针对该现象引入此前所述的滞后时间概念(t1)，则式(13)转化为

τ(t)=A″sin(ω(t-t1)-φ0)+τbias

(15)

其中，ωt1=2πft1=φ，可得t1值为23.1 ms。而引入滞后时间概念的好处是当激励频率趋于零时，滞后相角也同时趋于零，相当于使体系有了响应速度的概念，当激励的变化速度较慢时，系统响应基本跟上，几乎没有相角迟滞。若测量环节无滞后，则可知该系统磁场滞后与MRF滞后的总响应时长约为t1，即23.1 ms。

将该滞后时间t1分别代入式(10)和式(11)的线性与非线性模型进行仿真，绘制τ-I曲线，结果如图8所示。图8中仿真曲线随频率变化的趋势基本符合图6中的测试结果，说明测试结果的蝶形曲线主要由迟滞时间导致。比较图8a、图8b两模型仿真结果可知，图6中τ-I蝶形曲线平滑的上沿和下沿分别由滞后和非线性的τ-B关系所致。此外，对比图6与图8的剪切应力范围可知，非线性模型将图4中所示S形曲线描述得更准确，而线性模型在小电流情况下存在对剪切应力显著高估的问题。

(a)线性模型

(b)非线性模型图8 考虑滞后的仿真结果Fig.8 Simulation results considering hysteresis

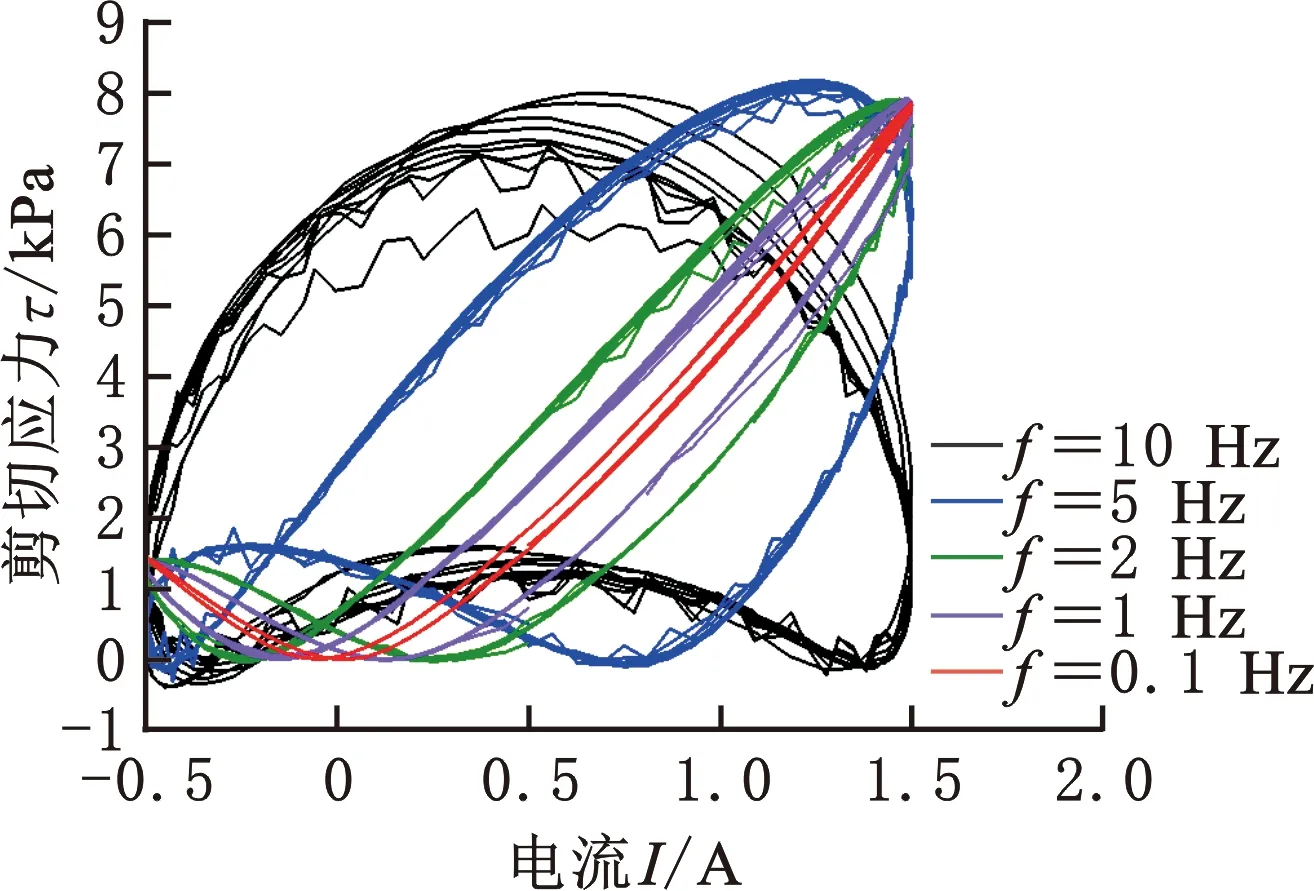
对于有偏置电流的情况，还可以细分为偏置大于振幅和小于振幅的两种情况，仿真和对比结果如图9所示(共10次循环)。可以发现，对于两种有偏置电流的情况，仿真结果均能够较好地与测试结果匹配，证明了仿真模型的有效性。

滞回曲线的本质就是曲线中出现了一对多的情况，即同一横坐标在曲线上有多个对应的纵坐标。仿真环节中B-I和τ-B均为一一对应关系，滞回曲线出现的主要原因就是滞后导致变量空间出现不对齐。再进一步就是由简谐振动的拓扑性质决定，即除波峰与波谷处，一个周期内每个值都有两个时间点与之对应。同一纵坐标的对应关系倍增原理也与之类似，本例中B-I为奇函数(B=0.1758I)，而τ-B则为偶函数，故而分别出现椭圆滞后环和蝶形滞后环。

(a)2 A偏置，1 A振幅测试

(b)2 A偏置，1 A振幅仿真

(c)0.5 A偏置，1 A振幅测试

(d)0.5 A偏置，1 A振幅仿真图9 考虑滞后的测试与仿真对照Fig.9 Comparison of tests and simulations considering hysteresis

此外，值得注意的是，蝶形曲线出现的原因是由于偶函数的翻折作用，故其两侧“翅膀”的滞后环面积并不完整。如图10所示，蝶形曲线实际的总滞后环面积St=S1+S2+2S3。

图10 蝶形曲线滞后环示意图Fig.10 Illustration of hysteretic loop with butterfly shape

3 结论

通过分析磁流变设备的各滞后环节，本文提出系统研究磁流变系统控制滞后及动态响应的方案，并主要就τ-I环节进行了测试与研究。由测试结果知，电流振幅主要影响滞回曲线的尺寸；偏置大小则影响曲线形状，并在其小于振幅时出现蝶形曲线；频率也通过滞后相角影响形状，且滞后相角随频率线性增大。据此，本文引入滞后时间t1描述相关行为，即剪切应力值对应t1前的电流值，对于本测试系统该值为23.1 ms。含该滞后项的非线性模型仿真结果能较好地描述系统动态行为。通过与线性模型的比较和分析，该模型还解释了蝶形滞后曲线的成因与特征。

综上所述，本文的分析、测试与建模工作为磁流变设备未来的滞后和动态响应研究奠定了基础。同时，若测量系统滞后可忽略，则可视该系统磁场滞后与MRF滞后的总响应时长约为t1，这为后续的系统优化提供了重要参数。后续研究将引入高斯计测量磁感应强度来分别独立研究系统的磁场和磁流变液滞后。