磁悬浮高速电机转子低频振动机理及补偿方法

2022-09-20马雪晴陈震民

中国机械工程 2022年17期

纪历马雪晴陈震民

1.杭州电子科技大学信息工程学院，杭州，311305 2.浙江中源磁悬浮技术有限公司，杭州，310011

0 引言

磁悬浮高速电机(本文特指磁悬浮轴承支撑的高速电机)的定转子之间无接触、无摩擦，转子转速普遍在100 000 r/min以上，可直接与高速原动机或工作机相连，取消了原有的增速/减速机构，能够大幅提高设备效率[1-3]。基于这一关键技术开发的磁悬浮鼓风机、磁悬浮压缩机等产品已经逐渐成熟，并在工业应用中取得了很好的节能效果。然而，在一些对可靠性要求较高的场合，由磁悬浮转子振动超限而导致的停机成为了制约磁悬浮产品推广的主要瓶颈。

针对这一问题，大量的研究工作着眼于解决由转子不平衡质量引发的同频振动[4-8]，如自平衡控制(最小力补偿)[9-10]和不平衡补偿(最小位移补偿)[11-13]。然而，根据大量的实测数据，在现场工况中磁悬浮转子的振动情况非常复杂，并不仅限于同频振动。一个较为常见的现象是，当设备振动超限跳停时，除了同频振动外，常伴随与转速无关的低频(50 Hz以下)振动。

文献[14]认为低频振动由磁悬浮系统中的非线性引发，认为非线性会使低频增益下降，导致系统不稳定。文献[15]发明了一种谐振质量阻尼器来抑制磁悬浮飞轮系统的低频振动。文献[16]提出利用干扰观测器对转子高速旋转时的低频振动进行观测和抑制。

目前，有关磁悬浮转子低频振动的研究较少，并不能很明确地解释其产生的机理。本文在已有研究基础之上，分析了导致转子低频振动的外部激励，结合磁悬浮系统的数学模型研究了该低频振动产生的机理，并提出了基于扩展状态观测器的振动补偿策略及稳定性判据方法。通过仿真与试验对得出的结论进行了验证，为磁悬浮技术在工业应用中的进一步推广提供了参考。

1 磁悬浮转子低频振动产生机理

1.1 磁悬浮系统的数学模型

本文以磁悬浮系统的数学模型为基础进行研究。经典的磁悬浮系统主要由控制器、功率放大器、磁悬浮轴承-转子、位移传感器四部分组成。其中，控制器是磁悬浮系统的核心，在工业应用中最为成熟的是PID控制器，其数学模型如下：

(1)

式中，KP、KI、KD分别为比例、积分、微分系数；Tf为不完全微分环节的时间常数，用来滤除信号中的噪声，避免微分环节过度放大系统中的噪声。

磁悬浮功率放大器[17]放大控制信号，实现对励磁电流的控制，该环节是典型的非线性设备，其工作过程会引入大量的高次谐波。但由于励磁线圈及磁悬浮转子系统本身具有较大惯性，高频谐波电流对系统影响较小，因此在设计控制系统时通常将其简化为一个线性的增益KA。

磁悬浮转子是系统中的被控对象，可根据磁悬浮轴承-转子的结构推导出悬浮力与励磁电流及转子位移间的关系，从而得到其数学模型。由于电磁力的非线性及结构上的耦合，磁悬浮转子是一个高阶的非线性系统，但对于刚性转子通常将其简化为一个SISO的线性模型，如下：

(2)

式中，m为转子单端的等效质量；Ki为电流刚度；Kx为位移刚度。

转子的振动量由传感器检测并转换为电压信号用于反馈控制，该环节用增益KS来表示，通常情况下传感器及其检测电路带有低通滤波器，可以由一个串联的一阶惯性环节来描述。

磁悬浮转子系统在工作时受到的外部激励主要来自转子的不平衡力，其形式表现为一个与转子同步旋转的力矢量：

(3)

式中，ep为转子偏心距(质心到形心的距离)；Δd为形心到旋转中心的距离，即动态偏心量；ωr为转子角速度。

此外，系统工作时不可避免地受噪声的影响，如数字系统A/D转换中引入的白噪声、功率放大器引入的开关噪声以及位移传感器调理电路引入的相关噪声，这些噪声将在微分控制器的作用下被放大，从而对系统造成不利的影响。为便于分析，本文将其统一等效为信号采样处的白噪声。

1.2 转子低频振动的仿真分析

在MATLAB中建立上述磁悬浮系统的数学模型，逐步加入激励，得到的仿真结果如图1所示。仿真主要参数如表1所示。

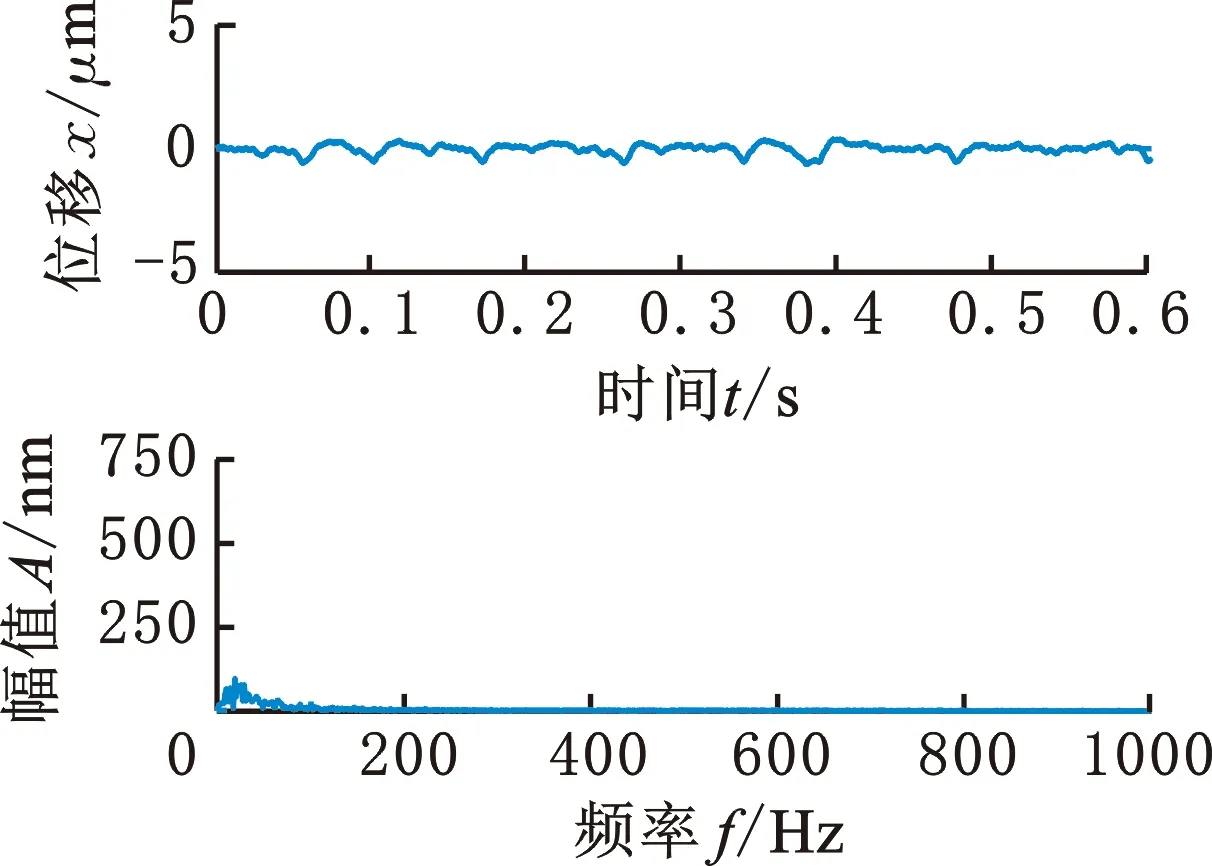
(a)无激励

(b)施加高斯白噪声

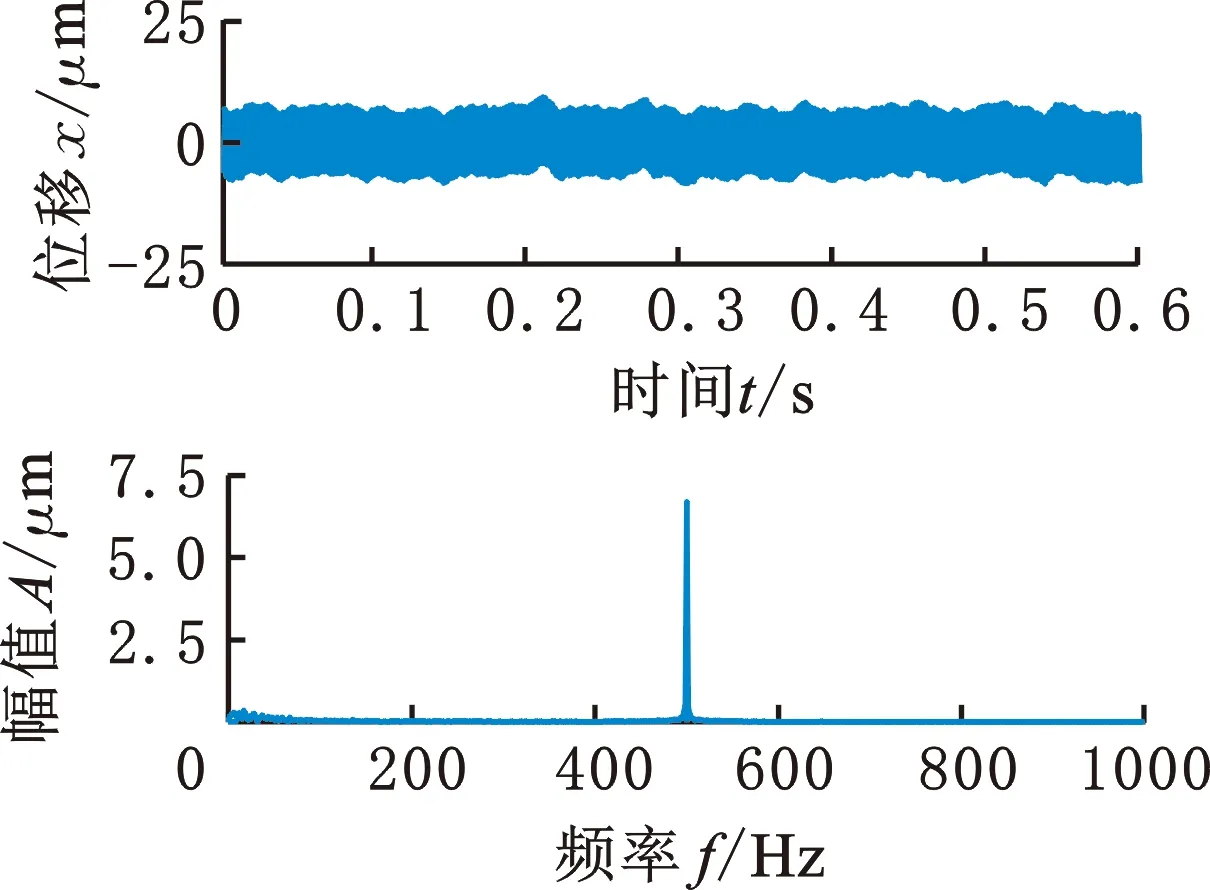
(c)施加不平衡力

(d)施加高斯噪声和不平衡力图1 不同激励下磁悬浮转子的振动波形及频谱特性Fig.1 Vibration waveforms and its spectrum for AMB based rotor with different noise excitation

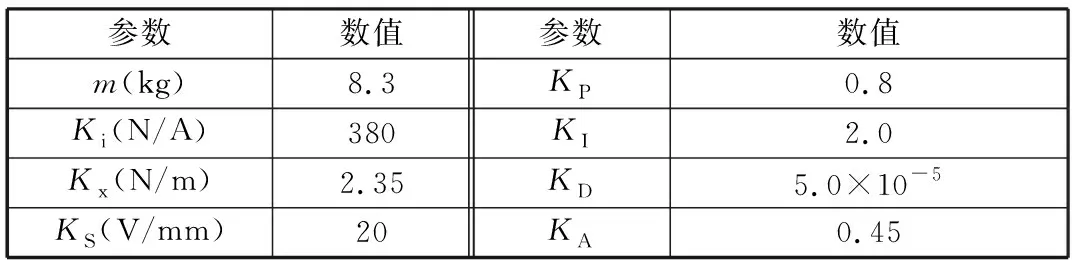
表1 磁悬浮控制系统主要参数Tab.1 The key parameters of the AMB system

图1a所示为无外部激励作用时磁悬浮转子稳态悬浮的振动波形，此时转子的振动信号极其微小，但仍可见微弱的低频振动。在转子位移信号采样处加入PSD(能量谱密度)高度为0.03的高斯白噪声，得到转子振动波形如图1b所示，可以看出，在白噪声的激励下，转子产生了明显的低频振动，主要频率成分集中在50 Hz以下，其中30 Hz为频率的峰值。在仿真模型中施加幅值为400 N、频率为500 Hz的不平衡力，模拟转子高速旋转时的不平衡振动，得到转子的振动波形如图1c所示，此时转子将产生很大的同频振动，低频振动则非常微小。最后，同时施加不平衡力与高斯白噪声，得到的转子振动波形如图1d所示，其中除占主导的同频500 Hz振动外，图1b中原有的低频成分也同时出现。

由图1可看出，磁悬浮转子振动信号中的固有低频成分与转子受到的不平衡力无关，而当系统中存在白噪声时该低频振动会明显增大。

进一步研究系统在白噪声激励情况下各环节的输出，如图2所示。图2a、2b分别表示系统中控制器环节与功率放大器环节的频率特性曲线，图2c、2d为控制器输出信号与功率放大器的输出电流波形。可以看出，白噪声通过PID控制器后，在中高频段出现了明显放大，而由于功率放大器的带宽限制，输出控制电流在高频段几乎完全衰减，与其传递函数的频率特性相一致。最后，由于磁悬浮轴承-转子本身具有很大惯性，高频成分在通过转子后完全衰减，得到图1b所示的位移输出。此外，由图2c、2d可以看出，图1中所示的低频成分在控制器与功放的输出中都存在，且占据主导作用。

(a)控制器频率

(b)功放环节频率

(c)控制器输出

(d)功放环节输出图2 磁悬浮系统控制器和功放环节的伯德图及白噪声激励下的输出波形Fig.2 Bode diagrams for AMB system and its output waveform

将表1中所有相关参数代入上述磁悬浮系统的闭环传递函数，计算其特征根，得到此时整个磁悬浮系统的主导极点，为一对共轭复根-205.37±42.54j，根据自动控制原理的基本理论计算该磁悬浮系统的固有频率，为33.38 Hz，与仿真结果非常接近，因此可以得出如下结论：磁悬浮转子的低频振动由闭环控制系统的固有频率决定，该振动会在噪声的激励下被激发，减小系统的噪声可以有效地抑制该低频振动。

2 基于ESO的振动补偿策略

扩展状态观测器(extended state observer，ESO)是在原有全阶观测器的基础上，将外部干扰及模型中的不确定性作为扰动，并将其扩展成为一种新的状态变量的方法，它不依赖于生成扰动的数学模型，具有很强的实用性。对于n阶系统，ESO的基本形式如下：

(4)

(5)

以磁悬浮转子系统为被控对象，将式(2)改写为状态方程的形式：

(6)

式中，x1为转子位移量x(t)；u(t)为磁悬浮控制电流i(t)；a=Kx/m；b=Ki/m。

考虑工程实现的简便性，将ESO中的非线性函数简化为线性，即gi(e1)=e1，则得出线性ESO的形式如下：

(7)

将模型式(7)与磁悬浮轴承系统状态空间方程式(6)作差，并记e1=z1-x1，e2=z2-x2，e3=z3-x3,即可得到误差方程：

(8)

根据式(7)可以得到加入ESO的磁悬浮控制系统，如图3所示。

图3 加入ESO的磁悬浮控制系统结构原理图Fig.3 The schematic diagram of AMB control system with ESO

当前关于ESO本身收敛性的理论已较为成熟，但是如图3所示，ESO的加入改变了原有磁悬浮控制系统的结构，必然导致系统的稳定性发生改变，需要进一步研究。

根据图3中控制系统的结构，将控制器输出量u改写为位移量Vx，得

(9)

将式(9)代入式(7)，可使ESO简化为一个SISO系统，推导出其传递函数为

(10)

为进一步简化设计过程，根据文献[18]，将参数β01、β02、β03配置成β01=3ω，β02=3ω2，β03=ω3的形式，则ESO系统的收敛性及磁悬浮系统的稳定性取决于系数ω。代入图3中所有传递函数及表1中的相关系数，以ω为单一变量求取嵌入ESO后磁悬浮闭环控制系统的特征根，并绘制出相应的主导根轨迹，如图4所示。可以得出当ω>530后，闭环系统全部特征根均位于左半平面，系统保持稳定。

图4 加入ESO的磁悬浮闭环系统主导根轨迹Fig.4 Root locus of AMB control system with ESO

3 仿真与试验

3.1 仿真分析

在MATLAB/Simulink中建立图3所示的磁悬浮控制系统，仿真涉及的主要参数如表1所示。首先验证控制系统对白噪声的抑制效果，在稳态悬浮时加入PSD高度为0.03的白噪声，当ESO的控制增益ω分别为500、600、10 000时，系统输出的转子振动波形及ESO的误差量e1、e2如图5a、5b、5c所示。从图中可以看出，当ω=500时，系统并不稳定，转子振动信号经过短时振荡后逐渐失稳。ω增加至600后，系统输出稳定，但由于增益较小，ESO并不能很好地抑制干扰，此时磁悬浮转子在白噪声的干扰下仍呈现了较大的低频振动，通过图5b、5c中展示的误差信号也可以看出，此时ESO对系统状态的估计还存在较大的误差，继续增大ω至10 000，此时ESO的估计误差基本为零，对比图1b中未加入ESO反馈的情况(振动峰值4.65 μm)，转子原有低频振动大幅下降(峰值1.12 μm)。

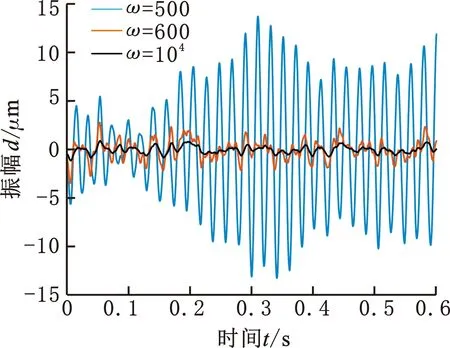
(a)转子振动波形

(b)误差e1

(c)误差e2

(d)加入500 Hz不平衡力图5 加入ESO的磁悬浮闭环系统仿真波形Fig.5 Simulation waveforms of AMB control system with ESO

在白噪声的基础上进一步加入500 Hz不平衡力，转子振动输出信号如图5d所示，图中蓝色波形为未加入ESO反馈的情况，黑色波形为加入ESO反馈后的输出情况，对比可知，加入ESO反馈后，转子的振动量大幅下降，由峰值14.5 μm下降至峰值6.9 μm，通过频谱图可以进一步看出100 Hz以下低频分量明显下降。由此可以得出结论：提出的基于ESO的扰动补偿策略可以很好地克服外界的扰动，降低磁悬浮转子运行时的振动量。

3.2 试验研究

为验证磁悬浮转子低频振动与激励的关系及振动补偿策略的有效性，本文在一台额定功率110 kW的磁悬浮高速永磁电机上进行验证试验。试验所用电机及测试环境如图6所示，电机及基础控制系统主要参数如表1所示。试验波形均为示波器实测数据后在MATLAB中绘制，为便于分析，绘制波形时将示波器测试的电压值直接换算为了转动量(传感器的灵敏度为20 V/mm)。

图6 磁悬浮高速电机及其试验台Fig.6 The prototype of AMB based motor and its test board

图7所示为稳态悬浮时，白噪声作用下磁悬浮转子的振动波形及频谱特性。图7a所示为使用单一PID控制时转子的振动波形，可以看出转子表现出了明显的低频振动，其峰值频率为35 Hz，与之前的理论分析非常接近，此时的最大振动量为13.8 μm，图中100 Hz的振动为电子整流器引入的干扰(两倍于工频)。在控制系统中加入ESO补偿，则在同样白噪声激励下，输出的振动波形如图7b所示。在ESO的作用下，转子的振动得到了一定的抑制，最大振动量下降至10.9 μm，较单一PID控制时下降约21%，且从信号频谱看，其低频振动被有效抑制。

(a)单一PID控制

(b)加入ESO图7 白噪声激励下转子振动波形及频谱特性Fig.7 Vibration waveforms and its spectrum for AMB based rotor with random excitation

同时对系统施加白噪声及100 Hz不平衡力激励，得到的输出波形如图8所示。图8a所示为单一PID控制时的波形，由于不平衡力起了主导作用，转子产生了很大的同频振动，达到36.2 μm，低频振动此时并不明显，但仍然存在。同样条件下，加入ESO补偿，输出如8b所示。此时转子振动大幅下降至20 μm，比单独PID控制下降了44.8%，可见本文提出的补偿策略对同频干扰同样适用。

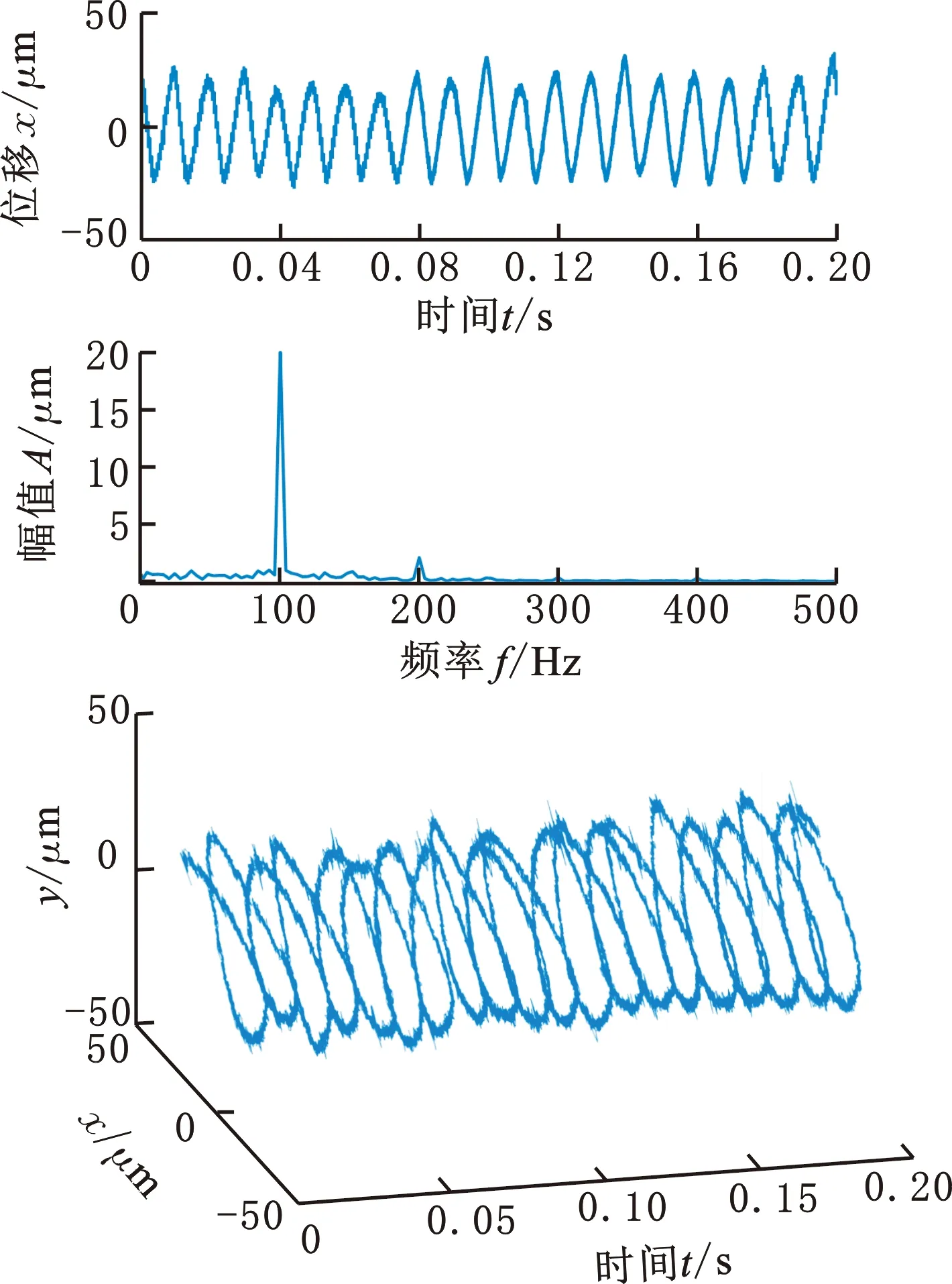
(a)单一PID控制

(d)加入ESO图8 白噪声与不平衡力激励下转子振动波形及频谱特性Fig.8 Vibration waveforms and its spectrum for AMB based rotor with noise and unbalanced force excitation

图9展示了转子在30 000 r/min高转速下的振动波形及频谱特性。图9a所示为使用单一PID控制方法时转子的振动波形，此时转子在不平衡力的激励下表现出了较大的同频振动并同时伴随有很小的低频振动，其最大振动量达到27.8 μm。同样转速下，加入ESO补偿，振动波形如图9b所示，可以看出在补偿器的作用下，同频振动明显减小，最大振动量下降至20.4 μm，下降幅度约26.6%。