分类例说线性规划思想在解题中的运用

刘海青

(福建省莆田第六中学，351111)

线性规划问题通常是指在线性约束条件下求线性目标函数的最值问题,具体体现就是图解法.利用图解法解题的步骤是:一画(画满足条件的平面区域)、二移(平移目标函数相应的直线)、三解(解方程组求出最优解)、四答(写出目标函数的最值).随着线性规划相关理论及应用的发展,其可行域、目标函数已不再限于线性区域或线性函数.

现在新教材中虽然删去了线性规划的内容,但作为一种重要的解题工具,线性规划思想在解决许多最值问题时有着明显的优势.下面撷取线性规划思想应用的几个视角,旨在探索题型规律.

一、在函数问题中的运用

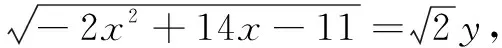
二、在三角函数问题中的运用

(C)f(x)的最小值为1

选项C，D均为最值问题，换元转化为二元函数来处理.

对选项C，由a∈[0,1],得a-a4=a(1-a3)≥0,即a≥a4,当且仅当a=0或a=1时等号成立.

同理b≥b4,当且仅当b=0或b=1时等号成立.所以a+b≥a4+b4=1,即f(x)的最小值为1，选项C正确.

对选项D，如图2，当a,b∈[0,1]时，a+b=1对应的图形是一条线段；a2+b2=1对应的图形是四分之一圆弧；a3+b3=1和a4+b4=1对应的图形是在线段a+b=1上方，且关于直线y=x对称的曲线段.

综上，选ACD.

评注本题判断选项D时，通过将问题转化，运用线性规划思想求解，颇为巧妙.

三、在向量问题中的运用

例3已知向量a,b满足|a|=1,|b|=2，则|a+b|+|a-b|的最小值为______,最大值为______.

解由三角不等式||a|-|b||≤|a±b|≤|a|+|b|及条件|a|=1,|b|=2,可得1≤|a+b|≤3,1≤|a-b|≤3.

设x=|a+b|,y=|a-b|,则x,y∈[1,3],且|a+b|+|a-b|=x+y,x2+y2=10.

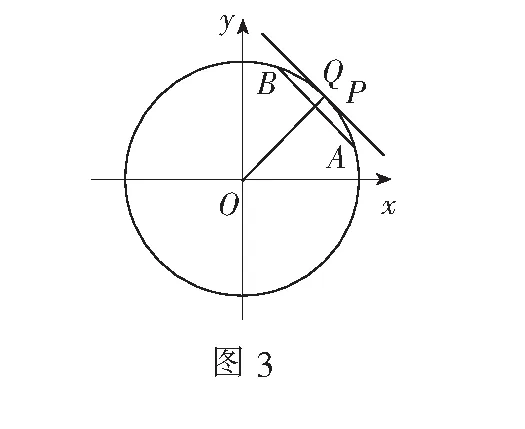
评注本题是通过设元,构造线性目标函数,运用线性规划思想求解的.

四、在不等式问题中的运用

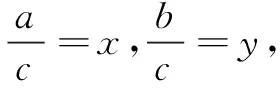
如图4，在平面直角坐标系xOy中，作出不等式组表示的平面区域.

由y=ex,得y′=ex.设切点坐标为(x0,y0),则切线方程为y-y0=ex0(x-x0),将原点坐标(0,0)代入，得y0=x0ex0.

又y0=ex0,所以ex0=x0ex0，解得x0=1,此时z=e，所以z的最小值为e.

评注本题是先将已知条件转换形式,换元后运用线性规划思想和导数的几何意义求解的.