应用“切线法”求解导数综合题

李 斌

(新疆乌鲁木齐市第二十三中学，830000)

导数的几何意义是导数的重要知识点之一,也是求解有关导数综合应用问题的重要工具.在解题过程中,若能应用或构造应用导数的几何意义,往往能使问题得到顺利解决.我们把应用导数的几何意义求解导数综合问题的方法权且称之为“切线法”,下面举例说明“切线法”在几个方面的应用.

一、平移化切

例1已知直线y=t与函数f(x)=2x+1和g(x)=2lnx+x的图象交于点A和B，则|AB|的最小值为______.

解函数g(x)的定义域为(0,+∞).

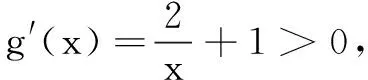
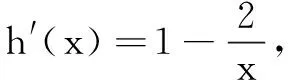
平移直线y=2x+1与g(x)=2lnx+x的图象相切于点B，此时|AB|最小.

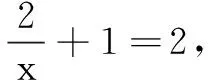
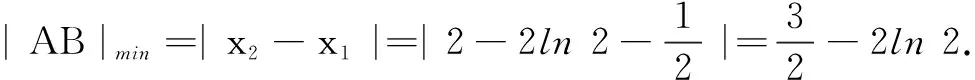
评注本题先将直线进行平移与函数g(x)的图象相切，确定此时|AB|取最小值，

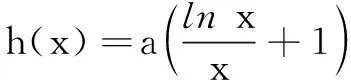
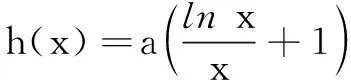
评注本题利用导数研究函数的性质，确定两个函数g(x)和h(x)的凸凹性，由两个函数的图象在点P(x0,y0)处有公切线时得到a=e,然后当a>e时，由h(x)的图象在公切线附近向上伸展，从而根据两函数的凸凹确定出函数f(x)必有两个零点.本题利用两函数图象的公切求解，颇为精彩.

三、利用图象与切线的位置关系

例3已知函数f(x)=xlnx+ax(a∈R),且y=f(x)的图象在点(e,f(e))处的切线与直线x+4y+3=0垂直.

(1)求函数f(x)的单调区间；

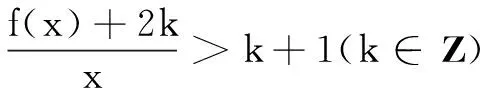
解(1)题设函数f(x)的定义域为(0,+∞)，f′(x)=1+lnx+a.由条件可得1+ln e+a=4,解得a=2.

所以f(x)=xlnx+2x,得f′(x)=lnx+3.

(2)由(1)知a=2.

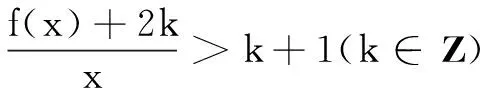
令φ(x)=xlnx+x,y=k(x-2),故问题等价于当x>2时，直线y=k(x-2)在φ(x)=xlnx+x图象的下方，求整数k的最大值.

先求过点(2，0)的函数φ(x)=xlnx+x图象的切线斜率k的取值范围.

由φ(x)=xlnx+x,得φ′(x)=lnx+2.设切点为(x0,y0)(x0>2),则有

消去y0,可得x0-4-2lnx0=0.

下面求x0的取值范围.

因为k∈Z,所以当x>2时，直线y=k(x-2)在函数φ(x)=xlnx+x图象的下方时，整数k的最大值为4.

评注本题第(2)问将问题等价转化为当x>2时，直线y=k(x-2)在函数φ(x)=xlnx+x图象的下方，然后求出过点(2，0)的函数φ(x)=xlnx+x图象的切线斜率k的范围，进而求得整数k的最大值.

四、利用切线放缩

例4(2021年全国高考题)已知函数f(x)=x(1-lnx).

(1)讨论f(x)的单调性；

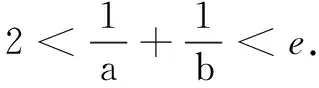
解(1)f(x)的定义域为(0，+∞).

又f′(x)=1-lnx-1=-lnx,当x∈(0,1)时，f′(x)>0;当x∈(1,+∞)时，f′(x)<0.所以f(x)在(0,1)单调增， 在(1,+∞)单调减.

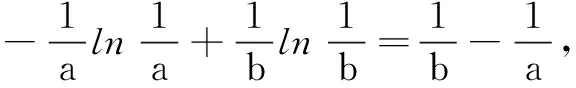
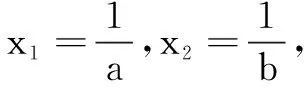
不妨设0

先证x1+x2>2.

再证x1+x2

由f(x)的图象在点(e,0)处的切线方程为y=-x+e,易知有f(x)≤-x+e,x∈(0,+∞).