圆锥曲线最值问题的常用求解策略——以一道圆中三角形面积最值题为例

戴德业

(江苏省溧水高级中学,211200)

本文以一道圆中三角形面积最值问题为例,从三角形面积计算的常见途径入手，通过多种解法,展示圆锥曲线最值问题的常用求解策略.

一、试题呈现

试题如图1，已知圆C：(x-1)2+y2=1，过原点O作直线l1,l2分别交圆C于A，B两点(A在x轴上方),若直线l1,l2的斜率之积为-2,求∆ABC的面积S的最大值.

二、求解策略

策略1函数思想

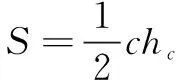
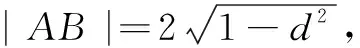
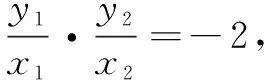
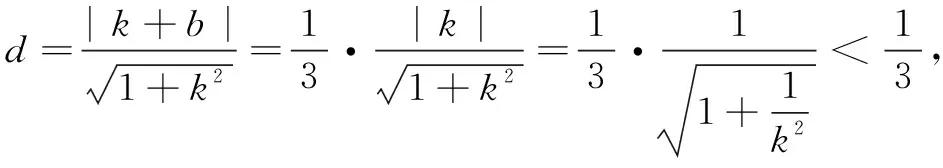
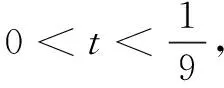
当直线AB的斜率不存在时,由圆心C在x轴上,可设直线AB的方程为x=m,点A(m,y0),B(m,-y0),其中m>0.

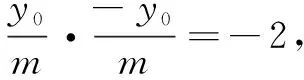
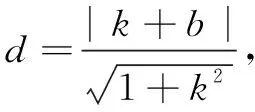
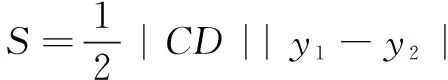
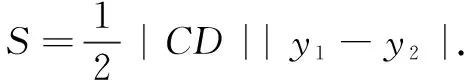
解法2由题易知直线AB的斜率不为0,可设直线AB的方程为x=my+t,点A(x1,y1),B(x2,y2).

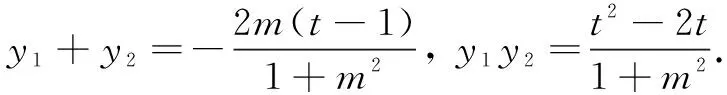
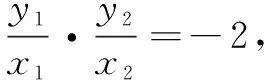
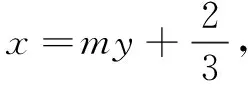
于是∆ABC的面积

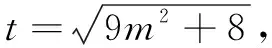
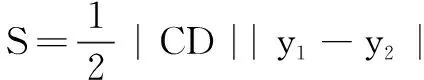
策略2不等式思想

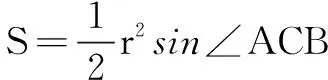
本题中的圆锥曲线是圆,由于圆的半径是已知的,所以只需要求出圆心角的正弦值范围.

解法3设直线l1,l2的斜率分别为k1,k2,则k1k2=-2.

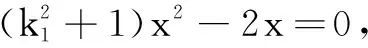
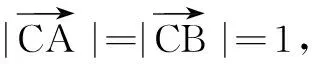
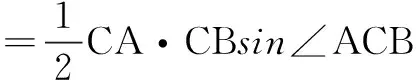
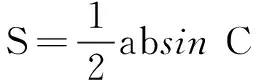
策略3数形结合思想

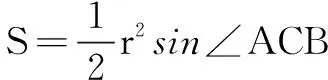
解法4设直线l1,l2的斜率分别为k1,k2,则k1k2=-2.

tan∠AOB=tan(α+β)

=-(tanα+tanβ).

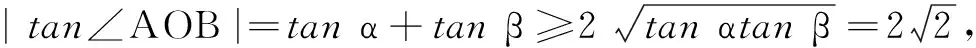
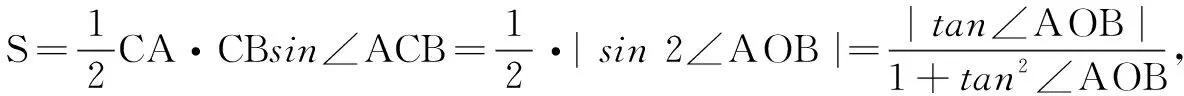
评注本解法运用基本不等式求出圆周角正切值的取值范围,利用平面几何中圆心角是圆周角的2倍的知识,进一步求得圆心角正弦值的范围.与前面3种解法相比,此解法运算量最小体现了不等式思想、数形结合思想和函数思想的综合运用策略.

综上,圆锥曲线中的最值问题的主要策略是函数思想和不等式思想.若能根据图形特征利用平面几何知识,则运算过程简捷明快,因此数形结合思想也是这类问题的一个重要求解策略.