多元表征 一题多解 深度学习

赵珊珊 陈建华

(江苏省扬州大学数学科学学院，225000)

众所周知,一题多解、一题多变是改善学生的思维定势,培养学生思维的广阔性、探索性、深刻性的有效途径之一．那么如何通过问题的多解,实现深度学习呢?本文基于多元表征理论,从数学内容知识表征和不同表征间的转换进行一些探讨．

一、相关理论与例题呈现

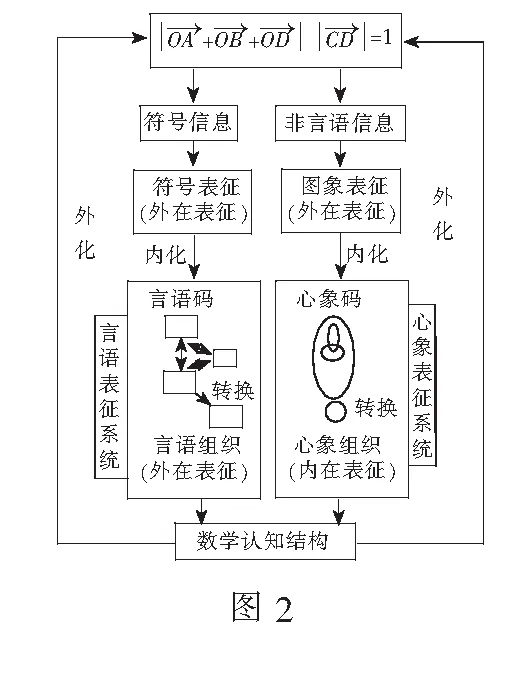
数学多元表征指将同一个数学学习对象用叙述性(言语化表征)和描绘性(视觉化表征)两种本质不同的形式表征．常见的表征形式有言语表征(用语言文字来描述问题情境、推理过程等)、图形表征(利用示意图、图片、线段图来描述问题情境、推理过程等)、操作表征、符号表征(使用数学符号、方程或表达式来描述问题情境、推理过程等)、情境表征等．如果问题信息具有多种表征方式,且不同表征之间存在着实质性的联系,那么通过系统图(如图1)可以多角度地分析理解．

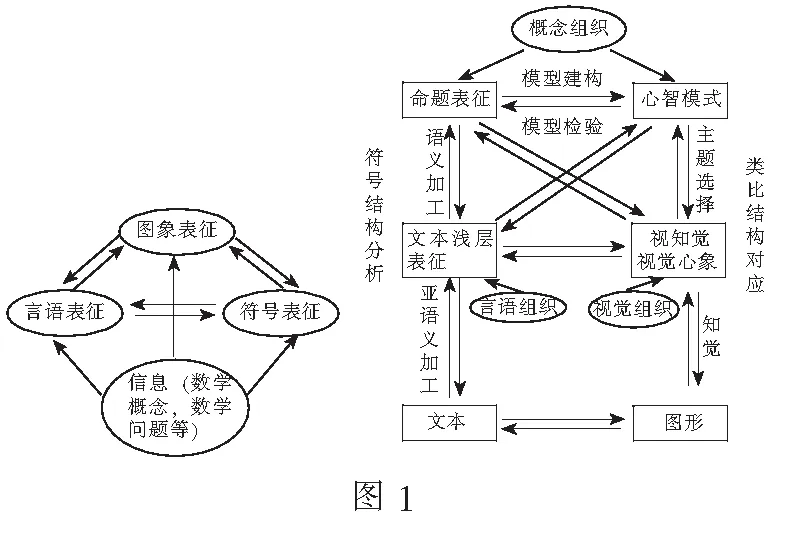
数学多元化表征及其转换的探究是进行数学学习和解题的一种表现．一道数学题通常是由题目的条件、解题的依据、解题的方法和题目的结论四个要素组成．从数学知识和方法角度,数学解题就是将“题目的条件和结论”通过恰当的表征,并建构逻辑关联,相关理论就是解题的依据,而知识的表征及其转换就是解题方法．问题知识表征的丰富性、转换的娴熟程度就是对相关知识和思想理解深度的表现．在表征转换过程中,经历如图1中所示的外在表征与内在表征的加工,达到深度学习的效果．下面以一道与平面向量相关的最值问题为载体展开探究．

二、数学表征下的解题分析

1.巧妙组合,借力三角不等式求最值

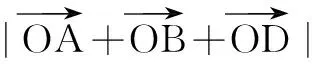
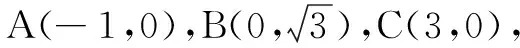
2.数形结合,利用距离公式求最值

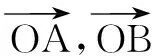
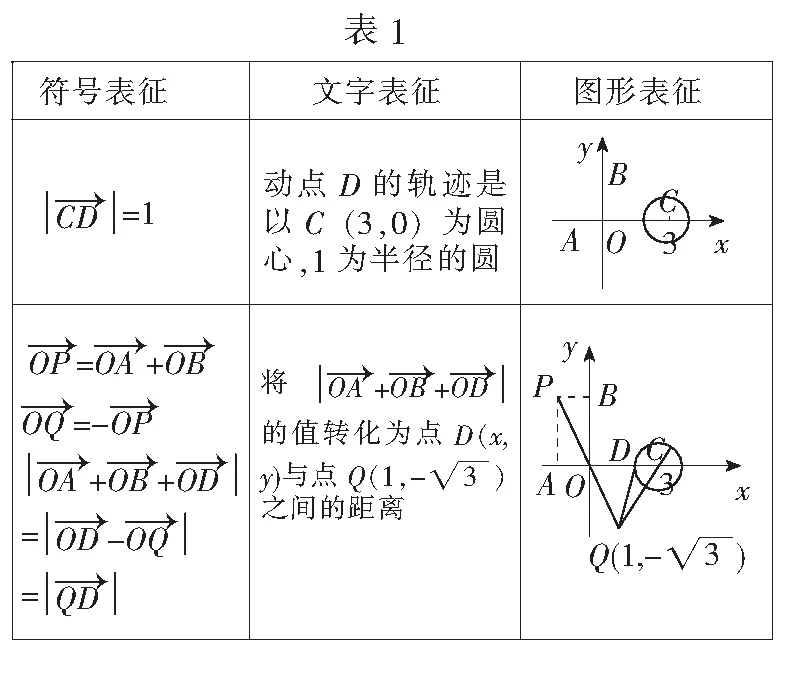
3.构造函数,转化为直线与圆相切求最值

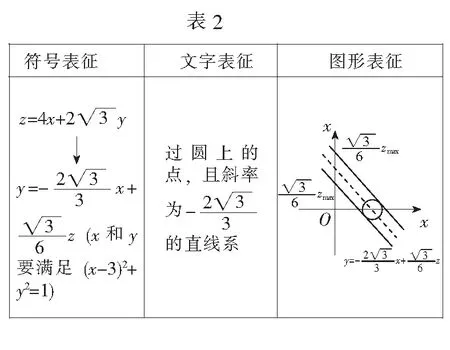
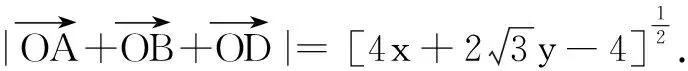
实际上,解法2和解法3的解题思路中,多元外部表征与转换过程就是数形结合转化的过程,这表明数形结合是有效解决数学问题的一种思想方法．必要时外化应用于形的数学学习对象,这表明不同的表征都有各自的作用,注重多种表征之间的关联与转换,能够促进知识之间的迁移．

4.添加参数,利用三角函数求最值

5.观察构造,巧借柯西不等式求最值

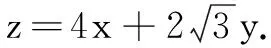
三、思考片语

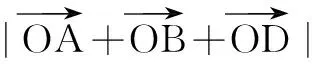
抽象数量关系及空间形式是数学的两个基本形态,而关系这是数学的本质,要学好数学,需要理解、更需要深度理解．掌握知识并且建立知识之间的关系是实现归纳、联想和推理的根基,对知识的认知也不能只停留于表面,而应该结合动作、听觉、视觉等具有图式表征、符号表征等高级表征方式的认识和运用才能进入深度学习状态,渐入“思维运动”的佳境．数学多元表征可以多层次抽象数学概念,多视角归纳数学概念,多维度建构数学概念,让数学概念的形成过程"看得见"．虽然目前多元表征的数学学习并没有可循之法,但只要教育者能够把握住这个内涵,运用多种形式与方法,引导学生在学习中进行实践再实践,认识再认识,创造再创造,深度学习就会自然发生．