分类例析将军饮马型最值问题

邓文忠

(陕西省洋县黄安初级中学，723307)

将军饮马问题中蕴含着轴对称思想:解决线段和的最小问题,往往将同侧其中一条线段关于某直线对称反射到该直线另一侧,从而将线段的和转化为两点之间线段最短或垂线段最短,即把两折线“转直”使问题获解.一般地,在同一平面内,通常将同侧点作关于直线的对称点转化问题;在空间中,往往将同侧点作关于面的对称点,同时伴随着将相关面展平,化空间问题为平面问题.现结合具体例子予以说明.

一、一个动点,“定-动-定”型最值问题

例1在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,P是线段BC1上的一动点,求A1P+PC的最小值.

解法1(代数法)

如图1,连结B1P,过点P作EF∥BC,分别交BB1,CC1于点E,F.

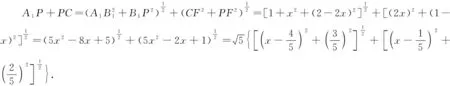
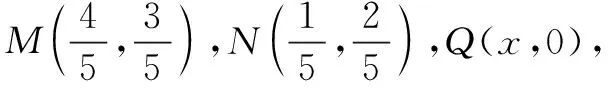
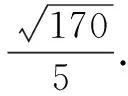
解法2(几何法)

因为A1P在面A1BC1上,PC在面BCC1上,把这两个面展平(如图3),则A1P+PC的最小值为A1C.

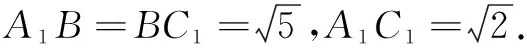
过点B作BE⊥A1C1于点E,过点A1作A1F⊥BC1于点F.

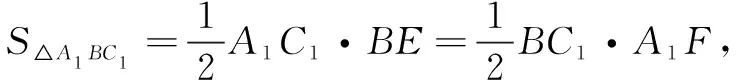
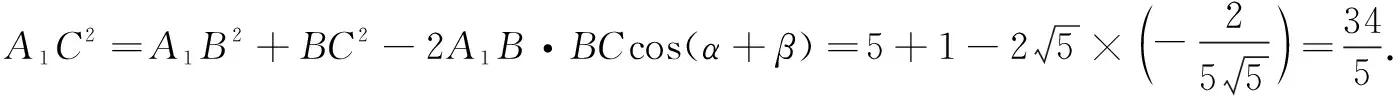
解法3(解析法)

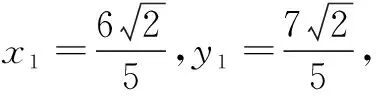
评注这两种解法是求最值的常用解法.代数法门槛低,切入容易深入难,需要一定的运算求解能力;几何法化空间为平面、化折为直,门槛高,起点高，落点低,需要一定的空间想象能力和逻辑思维能力.

例2已知正方体ABCD-A1B1C1D1的棱长为6,E是线段D1C1上的点,且D1E=2EC1,P是平面A1DC1内一动点,则D1P+PE的最小值为( )

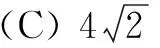
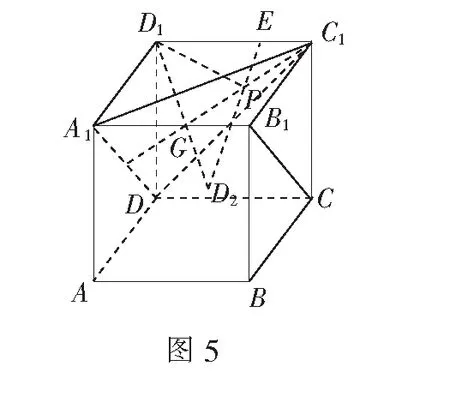
设∆A1DC1的外心为点G,连结D1G并延长至点D2,使D1与D2关于平面A1DC1对称.连结D2E交平面A1DC1于点P,则D1P+PE的最小值为D2E.

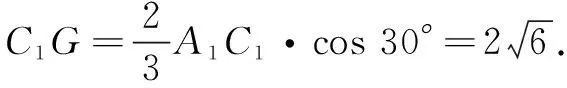
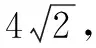
评注本解法将点D1关于平面A1DC1对称得点D2后,化点D1与E在平面A1DC1同侧为点D2与E在平面A1DC1异侧,然后将折线和D1P+PE拉直为D2E,是典型的“立几搭台、平几唱戏”.

二、两个动点,“定-动-动”型最值问题

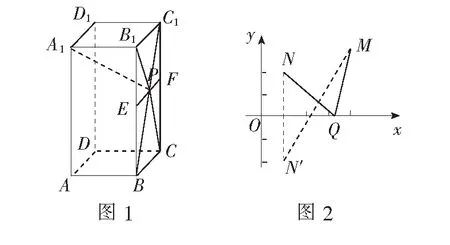
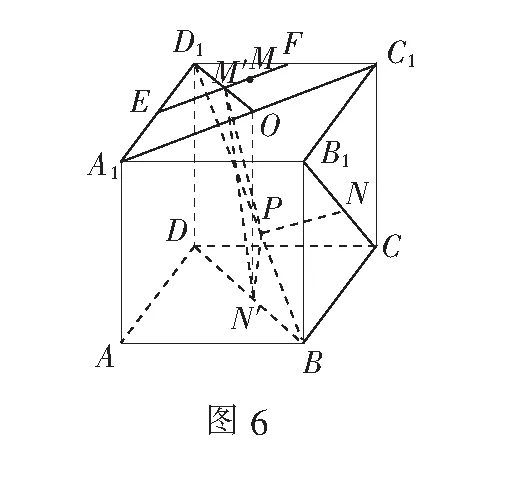
例3在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是棱A1D1,C1D1的中点,N为线段B1C的中点,若点P,M分别为线段D1B,EF上的动点,求PM+PN的最小值.

解如图6,先固定动点P,则PN为定值,要使PM+PN最小,只需PM最小.又由于PM′⊥EF,故当PM最小时,点M为EF的中点M′.再让点P运动,则问题转化为求PM′+PN的最小值.

由对称性,取BD的中点N′,则由∆PBN≌∆PBN′,得PN=PN′.于是问题转化为求PM′+PN′的最小值,即求线段M′N′的长.

评注对于双动点问题,常用的思维着力点是逐步调整原则,即采用分步走的策略.如本题中点P本身是动点,先将其暂时看成定点,利用将军饮马模型变PM+PN的最小值为求PM′+PN的最小值;再让点P动起来,借助PN=PN′,将求PM′+PN的最小值变成平面内求PM′+PN′的最小值,最终由平面最短距离原理使问题获解.在解决数学问题的过程往往充满着这种动与静的的对立统一,说明运动和静止在一定条件下是可以相互转化的.

例4在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则∆PEQ周长的最小值为______.

解如图7,作点E关于面A1B1C1D1的对称点S,取BC的中点T,连结PS,QT,ST.则∆PEQ周长=PQ+QE+EP=PQ+QT+PS≥ST.

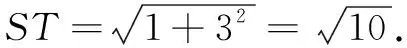
评注在本题的解答中,既有点关于线的对称,又有点关于面的对称,其本质是利用将军饮马模型等价转化问题,降低求解的难度.

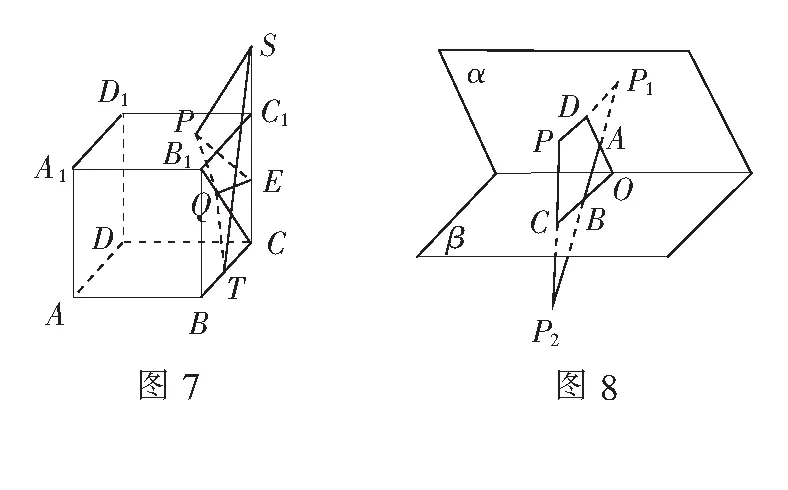
例5如图8,二面角α-l-β的大小为60°,点P到平面α，β的距离分别为2，3,点A∈α,B∈β,求∆ABP周长m的最小值.

解作点P关于平面α,β的对称点P1,P2,分别交平面α,β于点D,C.由对称性可知∆ABP周长m=AB+AP+BP=AB+AP1+BP2,且当A,B,P1,P2四点共线时,周长m取得最小值P1P2.

此时设平面PP1P2交直线l于点O,连结OC,OD.则有∠COD=60°,且由P,C,O,D四点共圆,得∠CPD=120°.

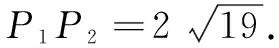
评注此题类似于问题“定角θ内有一定点P,角θ两边上各有动点A,B,求PAB周长的最小值.”求解的关键是将平面几何问题中的轴对称变换对类比为立体几何中的面对称变换.

三、两个动点,“定-动-动-定”型最值问题

例6九章算术中描述几何体“阳马”为“底面矩形,一侧棱垂直于底面的四棱锥”.现有阳马P-ABCD,PA⊥平面ABCD,PA=AB=1,AD=3,点E,F分别在AB,BC上,当空间四边形PEFD的周长最小时,三棱锥P-ADF外接球的表面积为( )

(A) 9π (B) 11π

(C) 12π (D) 16π

分析四边形PEFD的周长最小,由于PD为定值,故问题取决于PE+EF+FD最小.将侧面PAB展平,则问题转化为平面上的最值问题.

解如图9,把AP,PB剪开,使得∆PAB与矩形ABCD在同一个平面内.

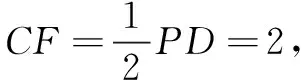
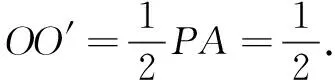
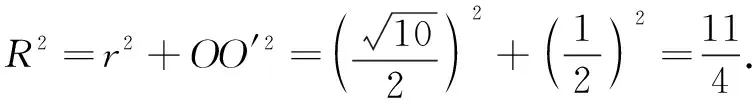
故三棱锥P-ADF外接球的表面积为4πR2=11π,故选B.