基于经验模态分解的螺栓连接状态敲击检测方法

刘俊燚，李宁，姜玉虎，李美求

(1.长江大学结构强度与振动研究所，湖北荆州 434023；2.江苏省油(气)井设备工程技术研究中心，江苏盐城 224000；3.江苏宏泰石化机械有限公司，江苏盐城 224000)

0 前言

螺栓连接广泛应用于工程现场连接结构中，螺栓连接结构容易拆装，降低了大型设备的运输成本。在含有螺栓连接的各种设备中，设备工作时螺栓的松动是一个不可避免的问题，全球每年约有20%的机械故障是由于螺栓松动引起的。并且在整个结构中，螺栓是比较薄弱的一个部位，一旦发生松动或者脱落，可能造成整个设备失效，严重的甚至威胁到人的生命财产安全。为避免螺栓松动，国内外学者对弹簧垫圈、双螺母、楔形垫圈以及非金属垫片等螺栓防松结构进行了大量相关研究，并证明了其在螺栓连接防松应用的有效性。但是现有防松结构的防松机制主要是靠摩擦防松或者张力锁紧防松，实际应用中存在安装拆卸不方便、螺纹强度差或者受温度影响显著等缺点。而开发一种低成本、简单可靠的螺栓在线监测方法既可以简化螺栓连接结构，又可以得到螺栓连接状态的及时反馈，进而保证整个系统的稳定运行。

常规的螺栓健康检测方法有敲击法、扭力扳手法、电阻应变片法等，其中扭力扳手法在工程实际中应用较为广泛。但是由于螺纹副与零件、螺栓与零件之间均存在摩擦且摩擦较为分散，扭力扳手测得的结果并不准确，同一规格的螺栓在相同扭矩下的预紧力误差甚至可以达到50%，并且受到螺栓安装位置的限制，扭力扳手在一些情况下无法对螺栓拧紧力进行快速检测。随着智能材料的发展，利用压电材料对螺栓的拧紧状态进行检测得到快速的发展。但是利用压电片对螺栓状态进行检测大部分应用于实验室条件，在工业上没有得到广泛的应用。通过在螺栓上粘贴电阻应变片，测量应变片形变可以直观地反映出螺栓的形变，在工业上得到较为广泛的应用。但是螺杆的表面是曲面，在其表面粘贴受到了一定程度的限制。在实际应用中，一个设备上安装的螺栓数目很多，若在每个螺栓上都安装应变片会带来较高的经济成本、时间成本。在螺栓状态监测方法的实际应用中，敲击法由于操作方便、对工作环境要求较低等原因可以较好地应用在实际工程中。

作为一种方便快捷的检测方法，敲击法最早的应用是使用硬币敲击构件表面，通过敲击声音判断构件是否有结构性损伤。在日常生活中，铁路工人通过敲击铁轨表面的声音判定铁轨是否有裂缝，建筑工人在铺地砖时用锤敲击地砖表面检查地砖下面是否有空洞。传统的通过敲击判断结构损伤的方法虽然简单，但是非常依赖人工经验，没有可以进行量化的标准。在理论上对敲击信号进行解释，最早是CAWLEY、ADAMS通过实验发现结构缺陷处被敲击时的声音信号与正常区域不同是因为敲击时力在结构中的传递发生了变化而造成的。WANG、SONG使用新开发的一维记忆增强卷积长短期记忆网络方法对铝制框架结构的敲击信号进行分析并证明了新方法对螺栓状态识别的有效性。肖强宏等基于敲击声音建立了一套可以对陶瓷产品进行结构缺陷在线监测的系统。

随着信号处理技术的快速发展，不断有新的信号处理方法应用于螺栓监测信号的分析中。傅里叶变换现已广泛应用于结构在线监测工作中，傅里叶变换是应用最为广泛的信号处理方法，对平稳信号的分析效果较好。但是现实中大部分信号都是非平稳信号，直接使用傅里叶变换对其进行处理，结果并不理想。为此，研究人员通过对傅里叶变换算法进行改进或者与其他信号处理方法相结合来更好地提取信号中包含的信息。在这些新的结构监测方法中，短时傅里叶变换、小波变换等方法得到了较多的应用，但是传统的短时傅里叶变换的时频窗口大小不变，没有自适应特性；小波分析虽然有可调的自适应窗口，但本质上仍然是一种窗口可调的傅里叶变换，依旧没有摆脱傅里叶变换的局限性。

美籍华人HUANG等在1998年提出了经验模态分解(Empirical Mode Decomposition，EMD)算法，这种方法对非平稳、非线性信号具有比较好的分析效果，可以对信号进行时频域上的自适应分析，EMD算法在HUANG等提出后广泛应用于结构健康领域。ZHOU等通过对含有螺栓的框架结构施加激励，并利用EMD能量损伤指标反映螺栓的连接状态，实验结果表明EMD能量指标对螺栓早期的松动更为敏感。PEREZ-RAMIREZ等通过EMD方式成功实现了对高层建筑振动信号中高频噪声的处理。周文强等利用EMD分解后的第一阶IMF分量构造能量损伤指标识别螺栓的损伤状态。

本文作者提出一种新的基于敲击声对螺栓连接状态进行分析的方法，使用经验模态分解对7种拧紧力矩下的螺栓敲击声信号进行分解，取分解后的前两阶IMF分量进行频谱分析，观察峰值点的频率值随螺栓拧紧力矩的变化趋势，并与原信号的频谱图进行对比，通过实验验证了该方法对螺栓连接状态检测的有效性。

1 理论分析

1.1 敲击信号检测机制

作为典型的非线性动力学问题，螺栓连接界面边界条件的时变性和接触非线性造成了连接界面刚度和阻尼的非线性。在实际生产工作中，螺栓连接中存在着接触、摩擦和预紧的耦合关系，在动态激励下，非线性耦合激励更为复杂，难以建立准确的数学力学模型。有学者研究发现螺栓预紧力的大小对螺栓法向接触刚度影响较大，预紧力越大，法向刚度越大，同时结构的固有频率随着结构刚度的增大而增大。因此可通过分析敲击螺栓连接部位信号的内在特征来实现对螺栓拧紧力矩的监测。作者主要是通过敲击信号检测螺栓的拧紧力矩，因而不对非线性动力学做细节上的分析，只寻找敲击信号随螺栓拧紧力矩变化的相关特征。

1.2 EMD算法原理

EMD算法将一个复杂的信号分解为若干个本征模式分量之和，这基于一个假设，假设任何复杂信号都是由一些不同的分量(IMF)组成。每个IMF分量都必须满足下面两个条件:(1)极值点个数和过零点的数量相同或最多相差1个；(2)分量的上下包络线关于时间轴局部对称。这样，任何一个信号就可以分解为有限个IMF之和，在此假设的基础上，任何信号都可以通过采用EMD方法来进行分解。而IMF可以按以下方法“筛选”获得：

(1)找到信号的所有局部极值点，将所有的局部极大值点用三次样条线连接起来，形成上包络线。

(2)同理，将所有局部极小值点用三次样条线连接起来形成下包络线，上、下包络线应将所有采集的数据点都包含进去。

(3)上、下包络线的平均值记为，求出

()-=

(1)

理想情况下，如果是一个IMF，那么就是()的第1个IMF分量。

(4)如果不满足IMF的条件，把作为原始数据，重复步骤(1)—(3),得到上、下包络线的平均值，再判断=-是否满足IMF的条件，如不满足则继续重复次，得到1(-1)-1=1使得1满足IMF的条件。记=1，此时，为信号()的第一个满足IMF条件的分量。

(5)将从()中分离出来，得到

=()-

(2)

将分离出来后，再将作为原始数据继续重复步骤(1)—(4)，直至得到()满足IMF条件的第二个分量。重复循环次，得到信号()的第个满足IMF条件的分量。这样就有

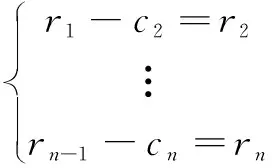
(3)

当变成一个单调函数，不能再从中提取出满足IMF条件的分量时，循环结束。这样由式(2)和式(3)得到

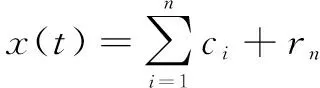
(4)

式(4)中：是残余函数，代表信号的平均趋势。

所以，通过经验模态分解可以把任意一个信号()分解为阶IMF分量和一个余项之和，螺栓的敲击信号是非平稳、非线性的信号，并且信号较为复杂，对其进行经验模态分解处理可以将信号包含的各分量分解为不同的阶数。

2 实验研究

2.1 实验设备

螺栓拧紧力矩检测实验装置如图1所示：实验设备包括M10的螺栓，螺母和垫片组合，尖头小锤，内六角扳手，垫在试件下的泡沫，量程10～200 N·m、测量精度为0.1 N·m的定扭矩扳手；实验所用数据采集设备为MPS-010602信号采集卡和YAVZ2环境声音传感器，信号采集卡的采样率为5～80 kSps，此实验中信号采样率为48 kHz，A/D精度为14位，录音环境在较为安静的室内。

图1 实验装置

2.2 实验过程

为获取螺栓连接在拧紧力矩不同的条件下，声音信号在时频域上的特征，用小锤敲击螺母侧边并使用声音传感器对敲击声信号进行采集。此次试验共采集了拧紧力矩分别为0、10、15、20、25、30、35 N·m时的螺栓敲击声信号，其中0 N·m即为螺栓完全松动的状态，采集信号时要保持敲击螺栓的力度不发生剧烈变化。对上述7种螺栓状态分别进行20次测试，增加样本数量的同时减少了偶发情况对数据集的影响。

3 实验结果及讨论

从图2中可以发现：在不同拧紧力矩下，敲击信号的时域信号图并不能很直观地反映出信号与拧紧力矩的关系。而频谱图可通过观察峰值点频率值寻找随拧紧力矩变化的规律，下面对信号做傅里叶变换，进行时频分析。

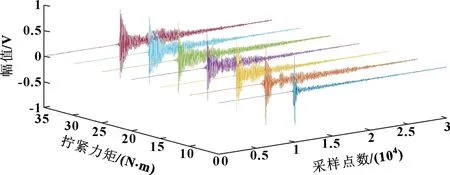
图2 不同拧紧力矩敲击下的时域信号图

3.1 频域分析

傅里叶变换是以时间为自变量的信号和以频率为自变量的频谱函数之间的一种变换关系。自变量时间和频率可以是连续的，也可以是离散的。傅里叶变换是一种线性的积分变换，这种变换是从时间转换为频率的变换或者从频率域转换到时间域上，一些在时域上没有明显特征的信号通过傅里叶变换可以简单地从频域上提取出相应的信息。

快速傅里叶变换是离散傅里叶变换的一种快速算法。对不同工况下的敲击信号进行快速傅里叶变换(FFT)处理，得到不同拧紧力矩下敲击螺母的声信号在频域上的特征。图3—图6为不同拧紧力矩下的频谱。

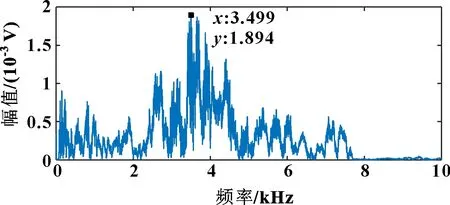
图3 拧紧力矩为0 N·m时的频域

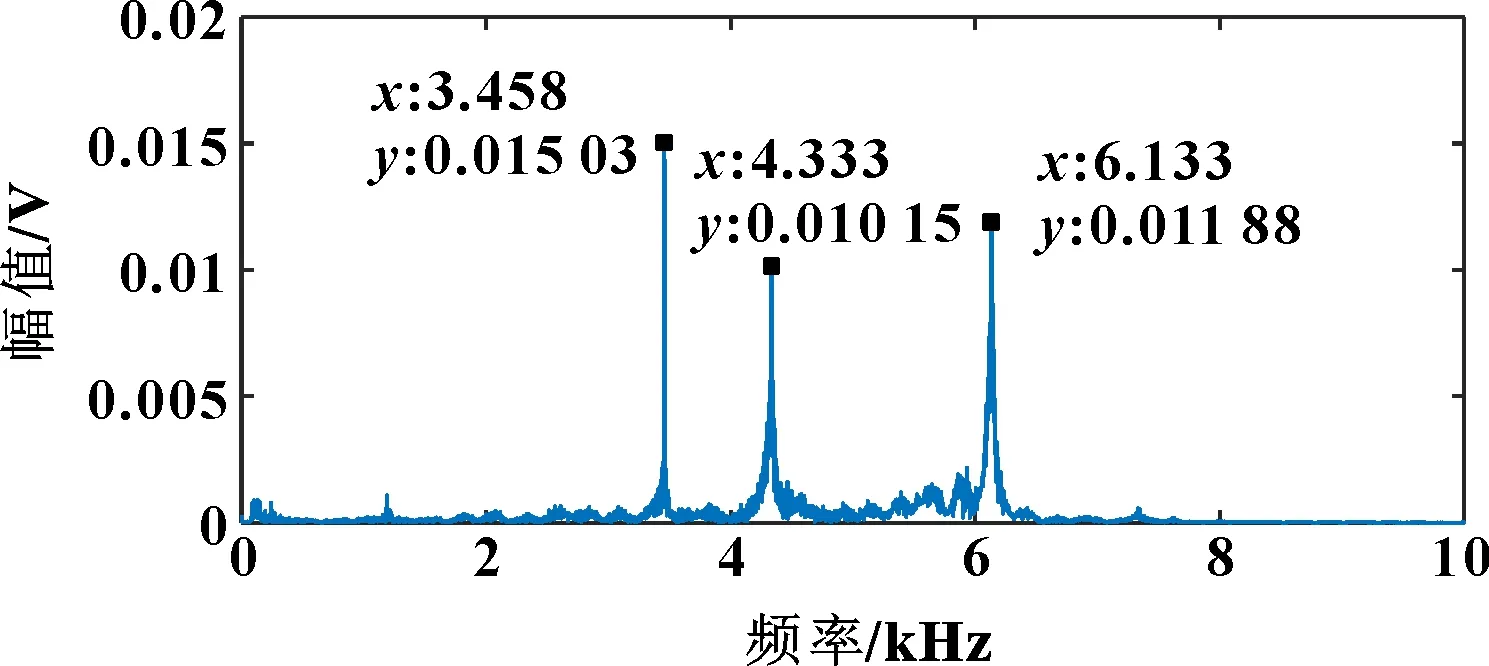
图4 拧紧力矩为10 N·m时的频域

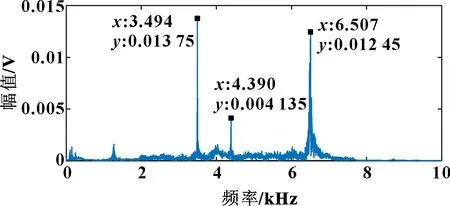
图5 拧紧力矩为20 N·m时的频域

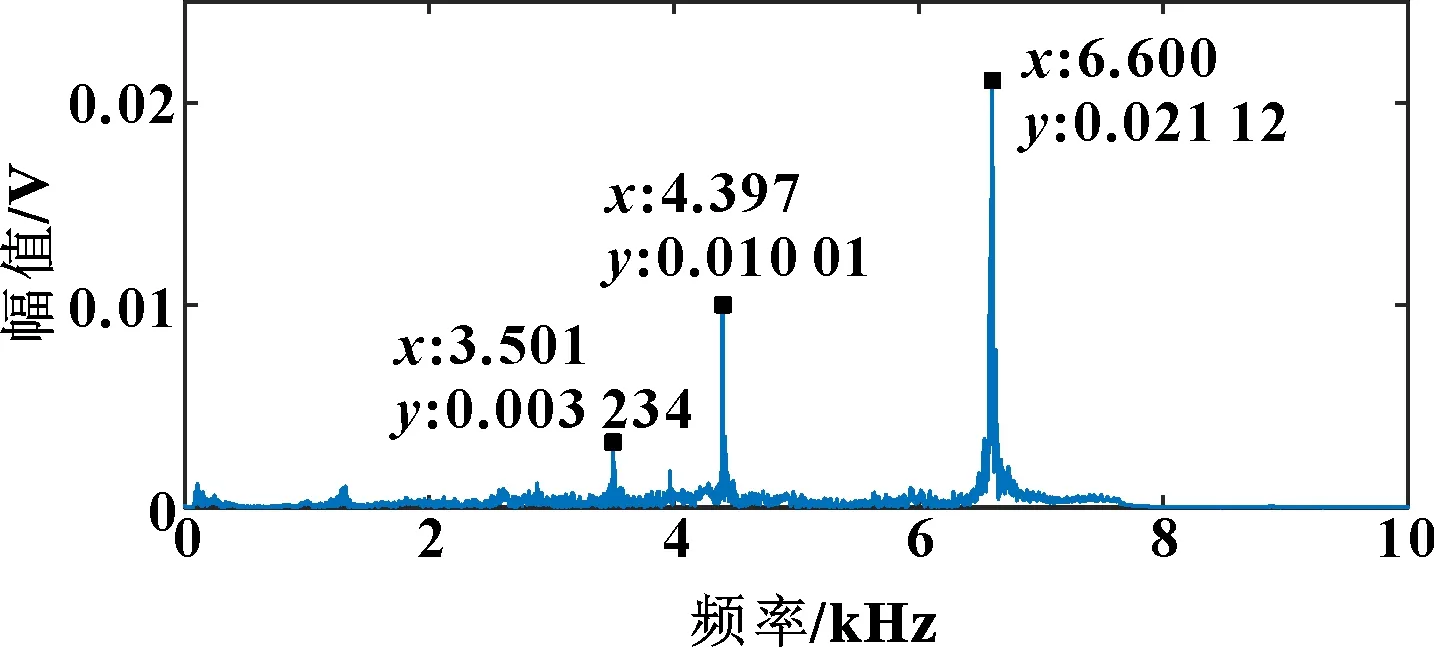
图6 拧紧力矩为30 N·m时的频域

图7反映了不同拧紧力矩下敲击声信号经傅里叶变换后的3个峰值点对应的频率随拧紧力矩变化的规律。

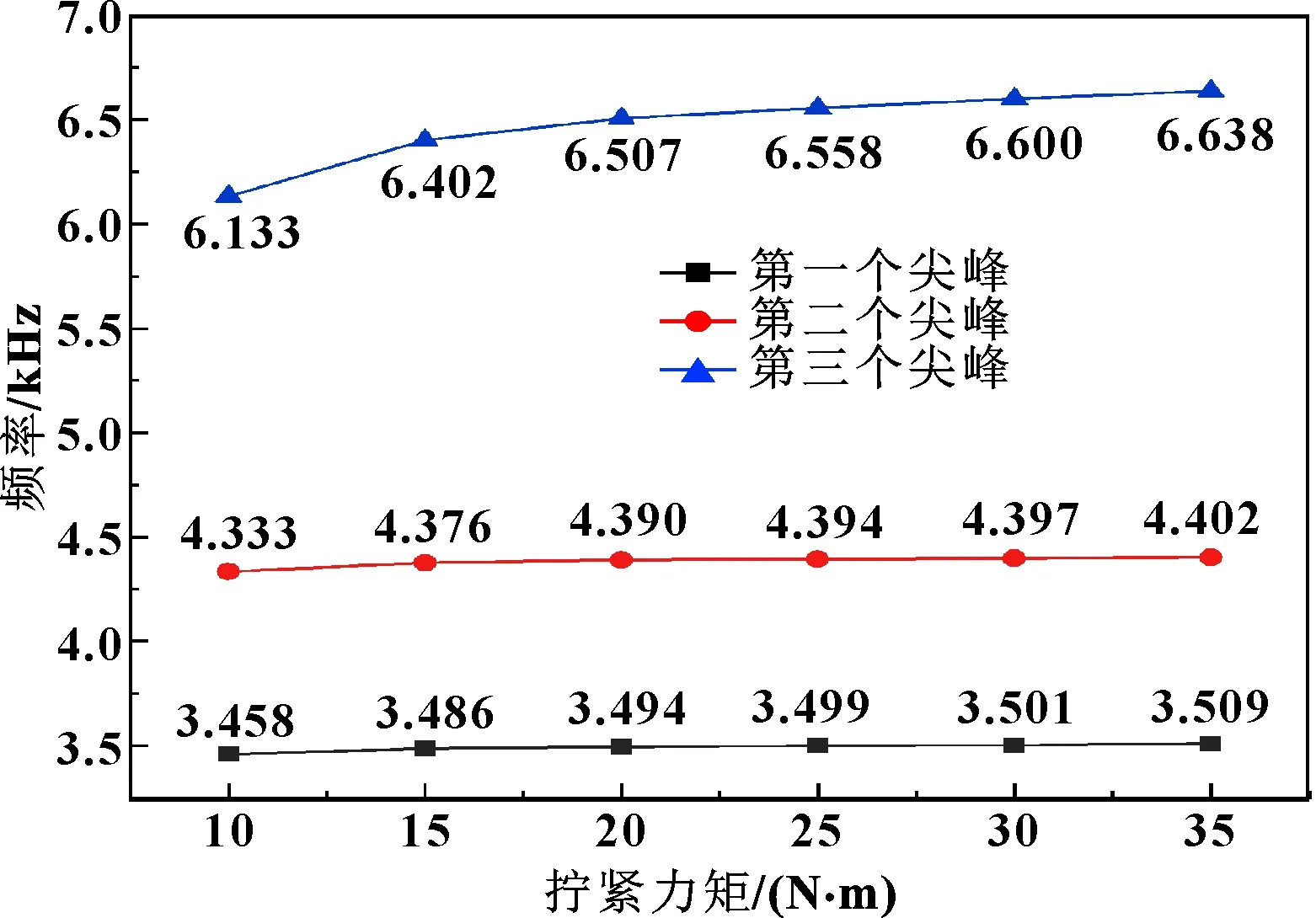
图7 不同拧紧力矩下3个峰值点的频率值

通过观察频谱图可以发现:除拧紧力矩为0时信号上只有一个峰值外，在螺栓处于有拧紧力的状态下，频谱图上会出现3个峰值。进一步观察还可以发现：3个峰值都会随着拧紧力矩的增大向高频方向偏移，这说明螺栓连接的刚度随拧紧力矩增大而增加。连接刚度主要是通过螺母与螺帽之间接触的紧密程度表现出来的，和拧紧力矩有直接的相关关系。

定义主频为原始波形信息经过傅里叶变换后所得到的二维频谱图中最大幅值所对应的频率。虽然3个峰值分别随螺栓拧紧力矩的增大而增大，但是主频值在频谱图上散布在不同的尖峰上，并没有确定的分布规律。

3.2 经验模态分解

由前文傅里叶变换分析结果可知，信号集中分布在由低到高的3个峰值上，可使用经验模态分解方法对信号进行分解，对分解后的IMF分量再做频域分析。经EMD分解过后，信号被分解为14个IMF分量，一般认为EMD方法是一种主成分分析方法，主要的故障信息集中在前几个IMF分量，故选用前两阶IMF分量对信号进行分析。图8为信号经过EMD分解后的前两阶IMF分量时域信号图。

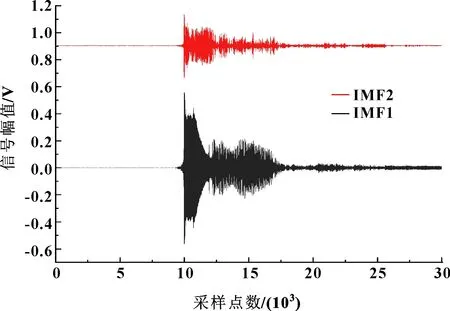
图8 前两阶IMF信号分量

获得信号的各阶模态分量之后，分别对前两阶IMF分量进行傅里叶变换，其峰值点的频率值如图9、图10所示。

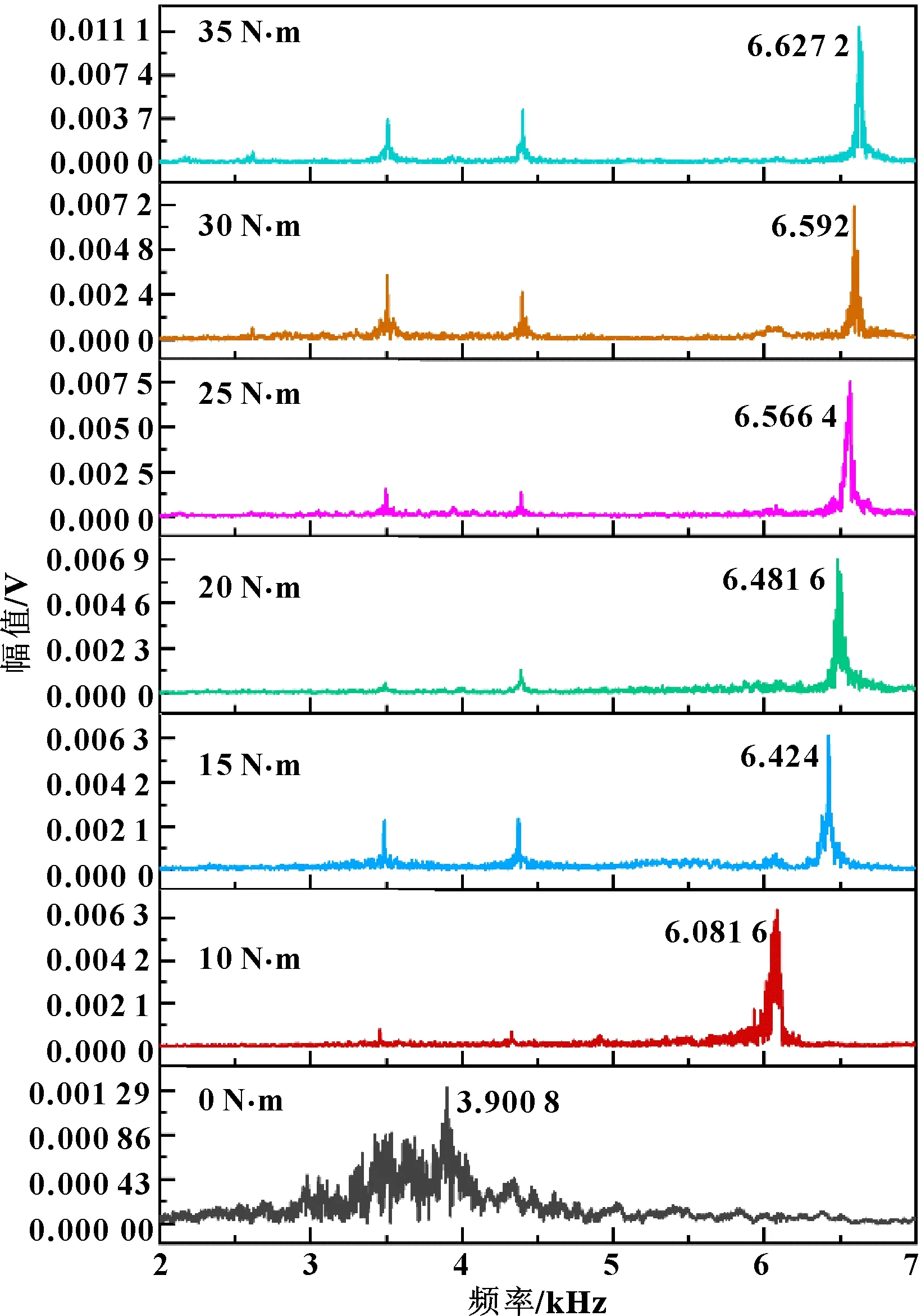
图9 不同力矩下IMF1信号峰值点的频率值

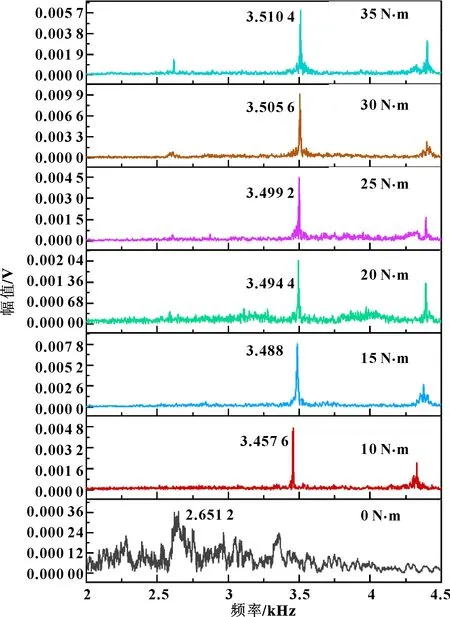
图10 不同力矩下IMF2信号峰值点的频率值

通过实验数据可以发现，信号前两阶IMF分量的峰值都随拧紧力矩增大而增大，并且从0到10 N·m的过程中峰值频率变化趋势最为明显。原因是IMF1的频率范围在螺栓连接的固有频率附近，螺栓从松动到拧紧状态转变时，螺栓连接界面之间的接触从表面微凸体之间的点接触变为相互嵌埋的状态，内部接触界面的结构发生了较大的变化；而在之后随着拧紧力矩增大到一定程度之后，大部分连接面的接触状态已转变为相互嵌埋的状态，接触刚度变化速度逐渐变慢。因而可以通过观察螺栓敲击信号的前两阶IMF信号分量来判定螺栓的连接状态，尤其是螺栓接近或者已经松脱时，峰值频率相较于螺栓正常连接状态有明显的变化。

4 结论

基于螺栓的敲击声信号提出了一种螺栓拧紧力矩的无损检测方法。通过上述研究，可以得出以下结论：

(1)在不同拧紧力矩下，螺栓的敲击声信号经傅里叶变换处理，在频谱图上可观察到有3个明显的尖峰，但是3个峰值点幅值之间的大小关系并没有很明显的规律；

(2)原始信号经EMD分解后，前两阶IMF分量都有很明显的峰值频率，并且峰值频率的大小都与拧紧力矩呈正相关，可以反映螺栓的连接状态；

(3)螺栓的拧紧力矩在从0到10 N·m的过程中峰值频率变化趋势最为明显，说明在螺栓即将松脱时，两阶模态分量的峰值频率对螺栓的连接状态变化更为敏感。

由于检测方法的便捷，该方法在工程实际中有较好的应用价值，但是通过观察信号两阶模态分量随螺栓拧紧力矩的变化趋势可以看出：随着拧紧力矩的增加，峰值频率增长速度逐渐放缓，在螺栓松脱程度比较小时，拧紧力矩对IMF1与IMF2峰值频率的影响都较小，对螺栓连接状态的检测精度较低；而螺栓接近松脱时，峰值频率变化曲线相对陡峭，此时，对螺栓连接状态的判断比较准确。对螺栓松脱程度较小时的状态可以作为接下来的研究内容。