介观尺度下风电齿轮的疲劳损伤演化机理

2022-09-15张建宇张侣倛

北京工业大学学报 2022年9期

张建宇，杨灿，张侣倛

(1.先进制造技术北京市重点实验室，北京 100124； 2.北京工业大学北京市精密测控技术与仪器工程技术研究中心，北京 100124； 3.聚光科技(杭州)股份有限公司，杭州 310052)

作为化石能源最主要的替代者之一，风能的开发、利用正受到越来越多的重视. 目前，风力发电机的设计寿命多为20年，但是由于机组设计未臻成熟，加之风场工况复杂多变，导致各地风力机的故障频发，甚至会造成严重的设备事故. 以市场的主流机型——双馈型风力发电机为例，作为连接风轮与发电机的“枢纽”，增速箱成为整个机组故障率最高的部件之一. 一些故障统计数据表明，由于运行工况复杂多变，接触疲劳已成为风电齿轮箱最主要的失效形式，并严重影响了整机的运行可靠性[1-3]. 因此，针对不同风载下的传动齿轮，开展疲劳损伤的演化机理研究，具有重要的工程应用价值.

疲劳失效是一个极其复杂的过程，其中既包含宏观力学因素，也涉及微观力学范畴，如材料的微观结构对损伤演化的影响. 为了更好地研究裂纹的扩展模式和损伤的演化过程，许多学者从介观尺度(即介于宏观和微观之间的尺度)，对滚动接触疲劳(rolling contact fatigue,RCF)问题进行了研究. 1994年，Ghosh等[4]首次提出Voronoi法，Ivano等[5]引入Voronoi单元模拟晶体组织. Mucklich等[6]将Voronoi图与真实的微观结构的相关量化指标进行对比，结果表明，Voronoi单元与金属材料的介观组织结构能够很好地吻合. 在此基础上，南京工业大学的史君林等[7]建立了符合实际情况的内聚力模型，通过批量插入零厚度的内聚力单元，模拟了多晶金属在没有初始损伤条件下的沿晶断裂过程.

近几年来，重庆大学学者建立了多种风电齿轮的损伤模型，得到了材料微观组织在滚动接触作用下的损伤演化过程，并基于连续损伤力学理论，研究了风电齿轮滚动接触疲劳区域的性能退化情况[8]，并对其疲劳寿命进行了预测研究[9-10]. Wang等[2,11]考虑了微观结构和晶体塑性，提出一种综合方法用来评估风电齿轮的RCF性能. Liu等[12]提出了一种风电齿轮RCF性能评估的数值模型，考虑了齿轮材料微观结构的各向异性和硬度梯度，并采用Fatemi-Socie疲劳准则研究晶体滑移系统的疲劳性能. Wei等[13]建立了一种考虑力学性能、硬度梯度和微观组织梯度影响的数值模型，以研究风电齿轮的接触疲劳损伤行为. Zhou等[14]建立了兆瓦级风电齿轮的整体有限元模型，考虑了齿轮几何结构、材料组织的不均匀性、非金属夹杂物的存在和齿面粗糙度，利用修正的Dang-Van多轴准则估计齿轮啮合过程中材料的疲劳失效概率，并研究了微观组织、夹杂物尺寸和表面粗糙度对齿轮接触疲劳行为的影响. Ghaffari等[15]建立三维有限元模型，在不同阶段分别采用损伤力学和断裂力学的方法，研究了齿轮裂纹的萌生和扩展. 张文博等[16]建立含夹杂物的风电齿轮有限元模型，从夹杂物的弹性模量、深度、尺寸以及排列位置等角度对风电齿轮的疲劳寿命进行预测，并从多角度探究夹杂物对其接触疲劳性能的影响. 谢俊杰等[17]建立接触疲劳裂纹扩展模型，模拟材料内部裂纹从萌生至扩展的全过程，得到其疲劳寿命及裂纹的扩展路径. 普渡大学的文献[18-19]从介观层面考虑微观晶粒结构的属性，如晶粒尺寸、形状、取向等，探究了疲劳裂纹的萌生和扩展，预测了滚动轴承的疲劳寿命，结果表明，晶界上产生的应力集中导致模型的临界剪切应力，显著高于各向同性的赫兹理论值. Slack等[20]在Voronoi多边形之间插入零厚度内聚力单元，探讨了晶界材料参数对接触疲劳损伤累积过程的影响，并通过材料S-N曲线获得了内聚力单元的加载次数，应用于滚动轴承介观模型的疲劳寿命预测中，结果符合Weibull分布. Ghodrati等[21]研究了晶粒大小、摩擦因数对滚动疲劳寿命的影响，通过移动载荷模拟车轮在钢轨上的滚动，并利用Jiang-Sehitoglu损伤模型预测了疲劳裂纹的萌生寿命. 以上研究成果均在一定程度上解决了介观尺度的建模问题，并对常规意义上的滚动接触疲劳进行了研究. 可见，材料的微观形貌对滚动接触疲劳行为和性能有着重要的影响[22]. 但值得注意的是，由于风电齿物在结构因素、材料性能和工况条件等方面的复杂性，其疲劳失效机理尚未得到根本的认识. 同时，很少有研究通过内聚力单元来模拟晶界对基体的割裂作用，并引入“表面移动载荷”模拟风电齿轮实际运转过程中的滚动接触效应，进而建立微观结构动态特性和疲劳损伤演化行为之间的关系.

针对以上不足，本文将从介观尺度对风电齿轮的疲劳损伤机理进行研究，模拟滚动接触疲劳损伤的演化过程. 基于Voronoi图与多晶体组织的几何相似性，采用法国Quey团队开发的Neper软件[23]建立齿面Voronoi晶粒介观模型，在晶粒内部添加内聚力单元，模拟晶界对基体的割裂作用. 根据损伤力学理论，对内聚力模型设置与损伤程度相对应的材料参数. 运用周期跳跃的加载方式，模拟齿面接触载荷的循环累积效应. 施加不同风速及摩擦因数下的表面移动载荷，模拟齿轮的滚动接触疲劳行为. 根据疲劳载荷下的损伤演化规则，预测风电齿轮的裂纹萌生寿命，并分析风速变化及齿面摩擦对疲劳寿命的影响.

1 介观尺度损伤建模的基本方法

1.1 晶粒及晶界模型的建立

宏观层面的疲劳损伤仿真，如基于线弹性断裂力学的疲劳裂纹扩展，多不涉及微观层面的力学性能差异. 实际上，对多晶体组织而言，晶粒之间存在着明显的各向异性，晶界位置和晶粒内部也存在显著的性能差异.

Voronoi图是一种描述宏观或微观实体的普遍结构，能够客观、全面地体现空间邻近关系，二维Voronoi图的数学定义[24]为

假设S平面上存在n个互不共线的点，点的集合P={p1,p2,…,pn}⊂R2，d(p,pi)表示p和pi两点之间的欧氏距离，定义

(1)

式中：V(pi) 所给出的对平面的分割，称为以P为点集的Voronoi图，即Voronoi多边形；pi、pj表示多边形的种子点，即晶粒发生元，如图1(a)所示，图1(b)为Voronoi晶粒，图1(c)为42CrMo金属的显微组织照片[25]，对比可见，Voronoi法建立的晶粒模型，与真实的金属材料介观组织高度相似.

图1 真实与仿真的多晶体模型

多晶体材料损伤的产生、发展，一般源自晶间界面的失效. 因此，本文关于风电齿轮的疲劳演化分析，也是以晶界处的缺陷萌生与扩展为前提. 目前，内聚力模型被广泛用于复合材料的界面行为分析，作为一种微观现象的假设，它可以通过选取合理的模型参数，在毋须预制裂纹的基础上，研究开裂路径上的缺陷萌生与扩展. 本文亦将采用内聚力单元，模拟晶界对基体的割裂作用，其基本原理如图2所示. 其中CPE3代表二维线性平面应变单元(本文用于晶粒建模的单元)，COH2D4即为零厚度的内聚力单元，其界面通过内聚力黏结在一起，视为零厚度. 其上、下表面与晶粒单元CPE3的边界相连接，在承受外载荷的情况下，界面间出现相对张开位移，如图2(c)所示. 当张开位移超过临界值，代表损伤开始形成，其本构关系“牵引力- 张开位移准则”详见1.2节的损伤判据.

图2 内聚力单元原理示意

本文选择线性平面应变单元CPE3，完成晶粒内部的有限元建模，划分结果如图3(a)所示. 在每2个晶粒之间，插入零厚度的内聚力单元COH2D4，模拟晶界的作用，结果如图3(b)所示，其中红线即代表插入的晶界单元.

图3 介观组织有限元模型

1.2 内聚力模型的损伤判据

根据Rabotnov[26]提出的损伤力学理论，引入损伤变量D描述材料的损伤状态，其中D=0表示材料无损，D=1则表示完全损伤.计入损伤因素后，材料承受的有效应力为

(2)

在实际的仿真过程中，可以根据“应变等效性假设”[27]间接描述D的作用，即：在应力作用下，损伤材料的本构关系与无损状态相同，单元未损和损伤发生时的应变是等价的，只需将其中的真实应力换成有效应力，存在关系

(3)

也可将其转化为刚度退化的形式

(4)

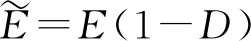
(5)

由于本文以晶界作为缺陷萌生的起源，因此需要针对晶界(文中的内聚力单元)建立损伤判据.内聚力模型是建立在损伤力学基础上的，其本构关系通常称为“牵引力- 分离位移准则”.目前常用的分离准则，主要包括指数型和双线性2种.其中，双线性模型是1998年由Mi等[28]提出的，作为一种简单有效的内聚力模型，该模型已经获得了广泛的应用，其基本原理如图4所示.其中横坐标表示分离位移，纵坐标表示牵引力，Di(i=1，2，…)即为式(2)～(5)的损伤变量D.

图4 双线性牵引力- 位移分离曲线

在单元加载的过程中，当界面分离位移δ从0开始增大，直至临界位移δ0时，单元承载的应力值t也从0线性增长到临界牵引力t0(即图中的路径1，K0为单元刚度值)，该阶段为线弹性段，无损伤发生；当分离位移δ继续增大，单元承载的应力值将沿路径2线性下降，当分离位移达到失效临界值δF，单元承载的应力值变为0，即认为内聚力单元失去承载能力，缺陷形成，因此路径2为双线性模型的损伤阶段；如果在损伤进程的某一时刻卸载，内聚力单元将沿图中的3、4、i等中间路径返回初始状态；如果再次加载，内聚力单元重新按照路径3、4、i的反向线性增长.由此不难看出，单元刚度以及临界牵引力值都发生了退化，是为单元损伤的累积过程.

内聚力模型的失效，不但可以通过分离位移与失效临界位移的关系进行判断，还可从能量角度，通过断裂能与其临界值Gc的关系加以确定.根据图4的双线性关系，内聚力模型的临界断裂能可表示为

(6)

可见，Gc的初始值即为图4中2条实线围成的三角形面积.根据内聚力单元的双线性模型，在疲劳损伤演化进程中，单元的刚度、临界断裂能以及临界牵引力同时发生线性退化，退化过程的参数变化表示为

(7)

(8)

(9)

2 风电齿轮的损伤演化预测方法

2.1 齿面接触区的承载特性

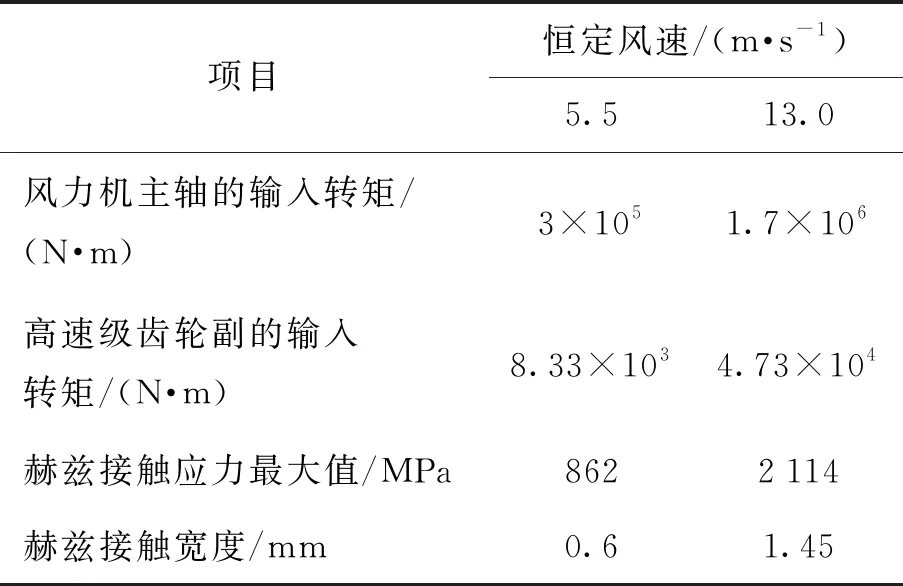
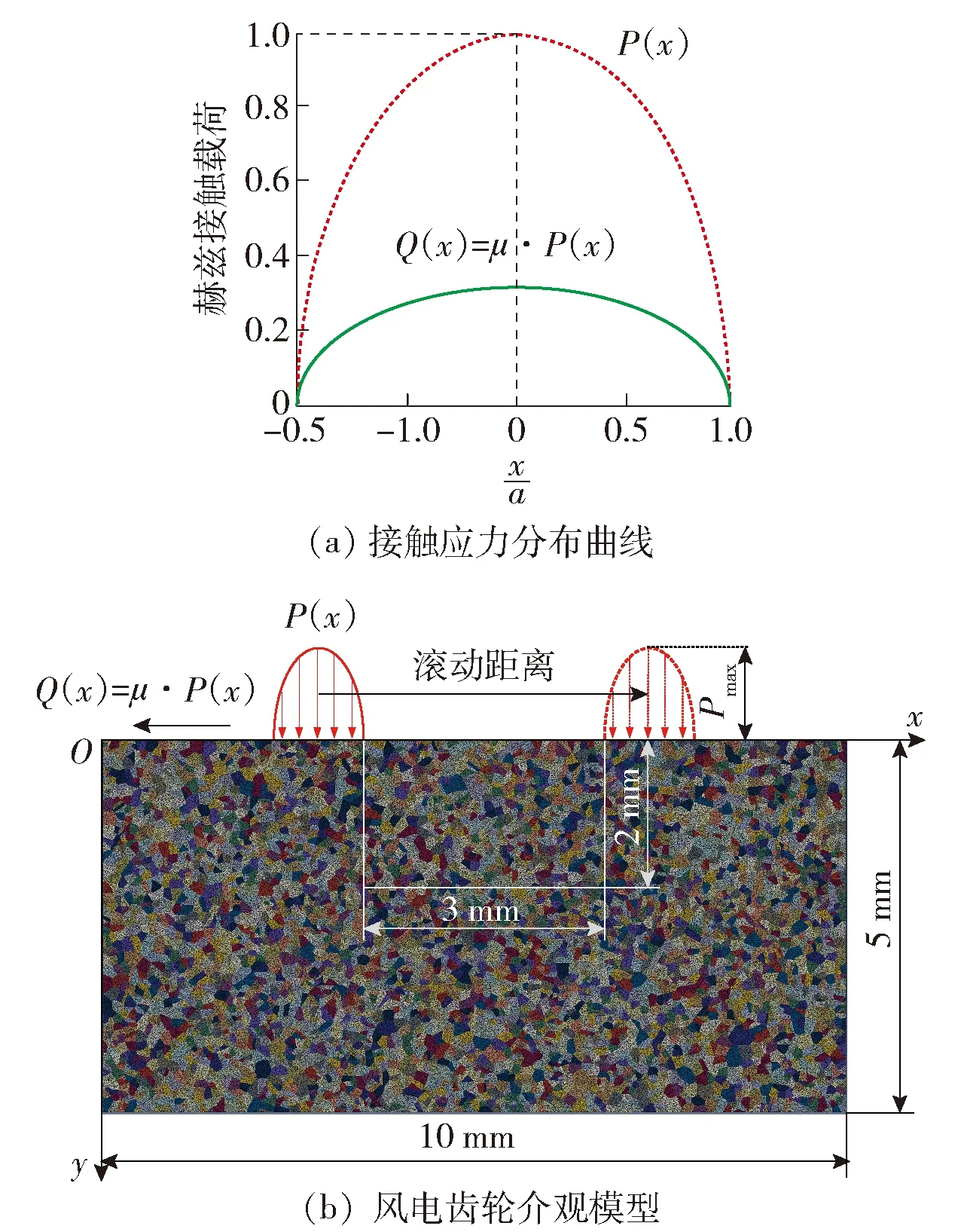
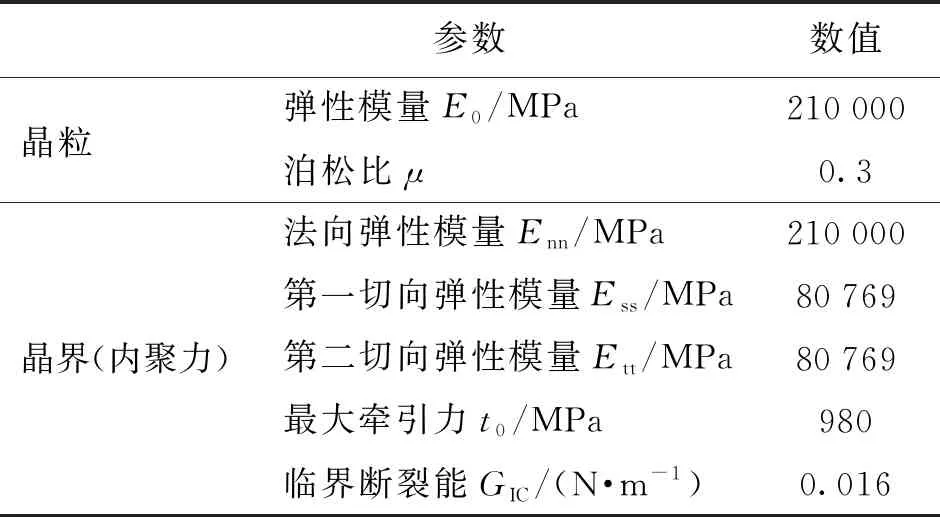
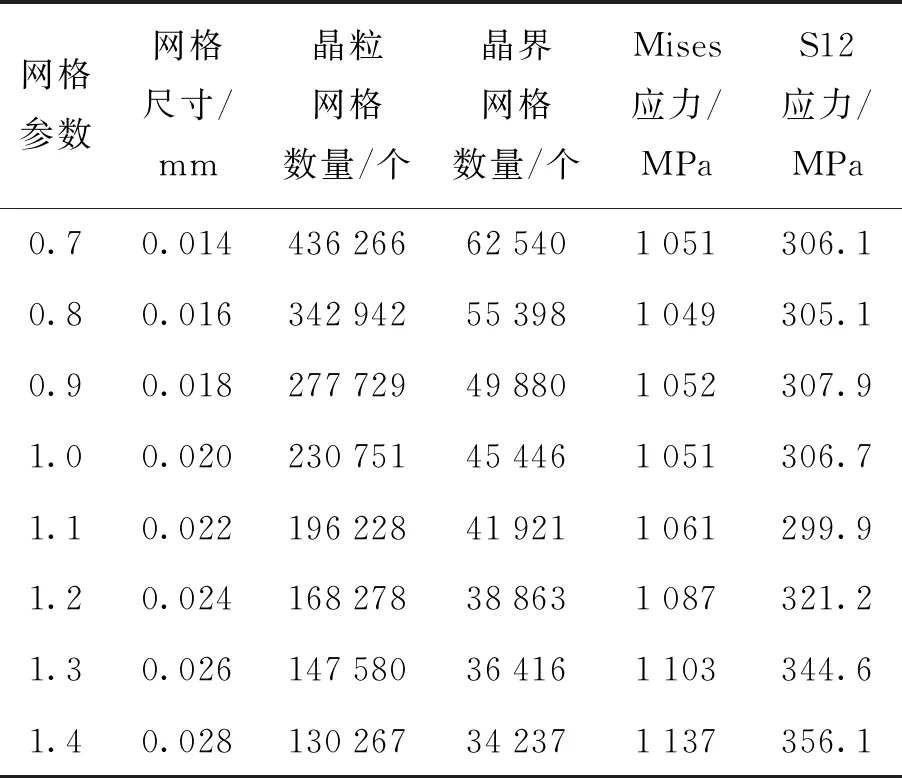
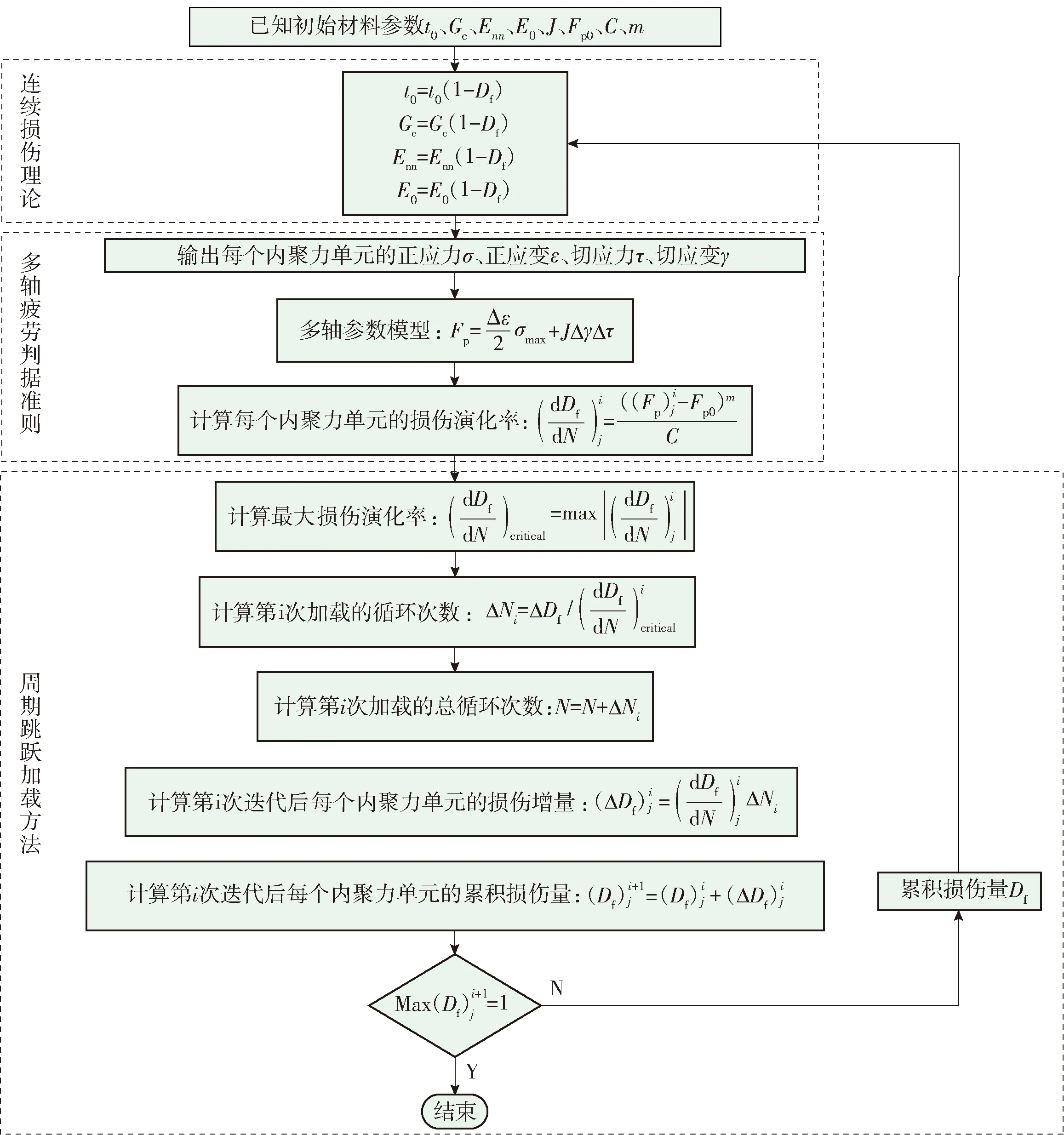
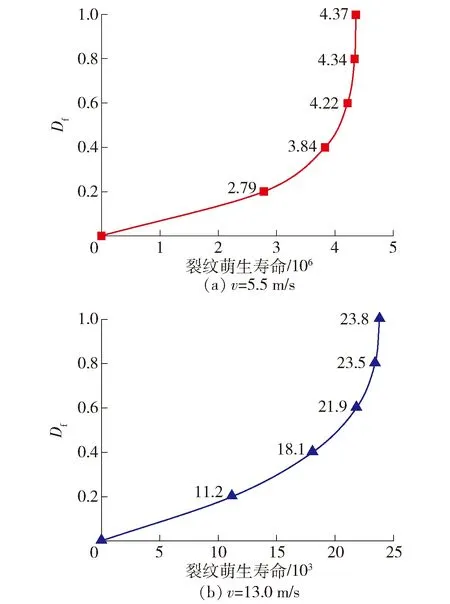
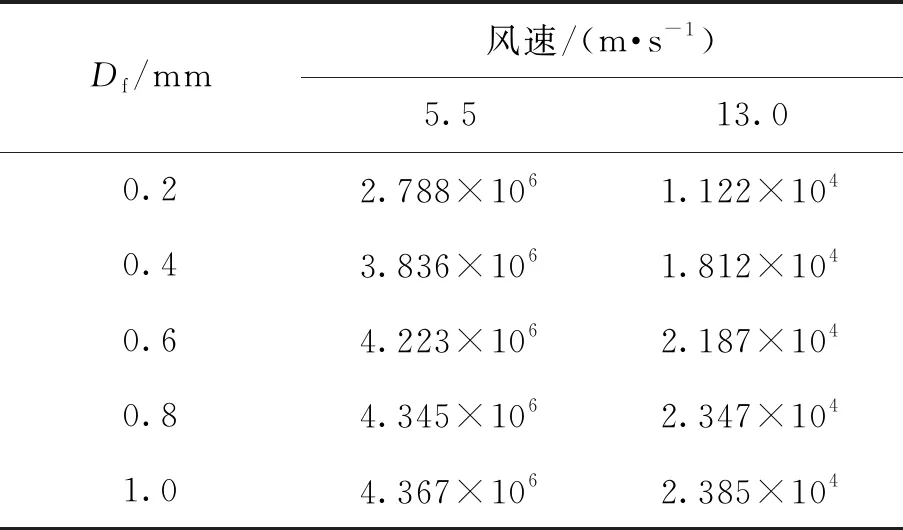
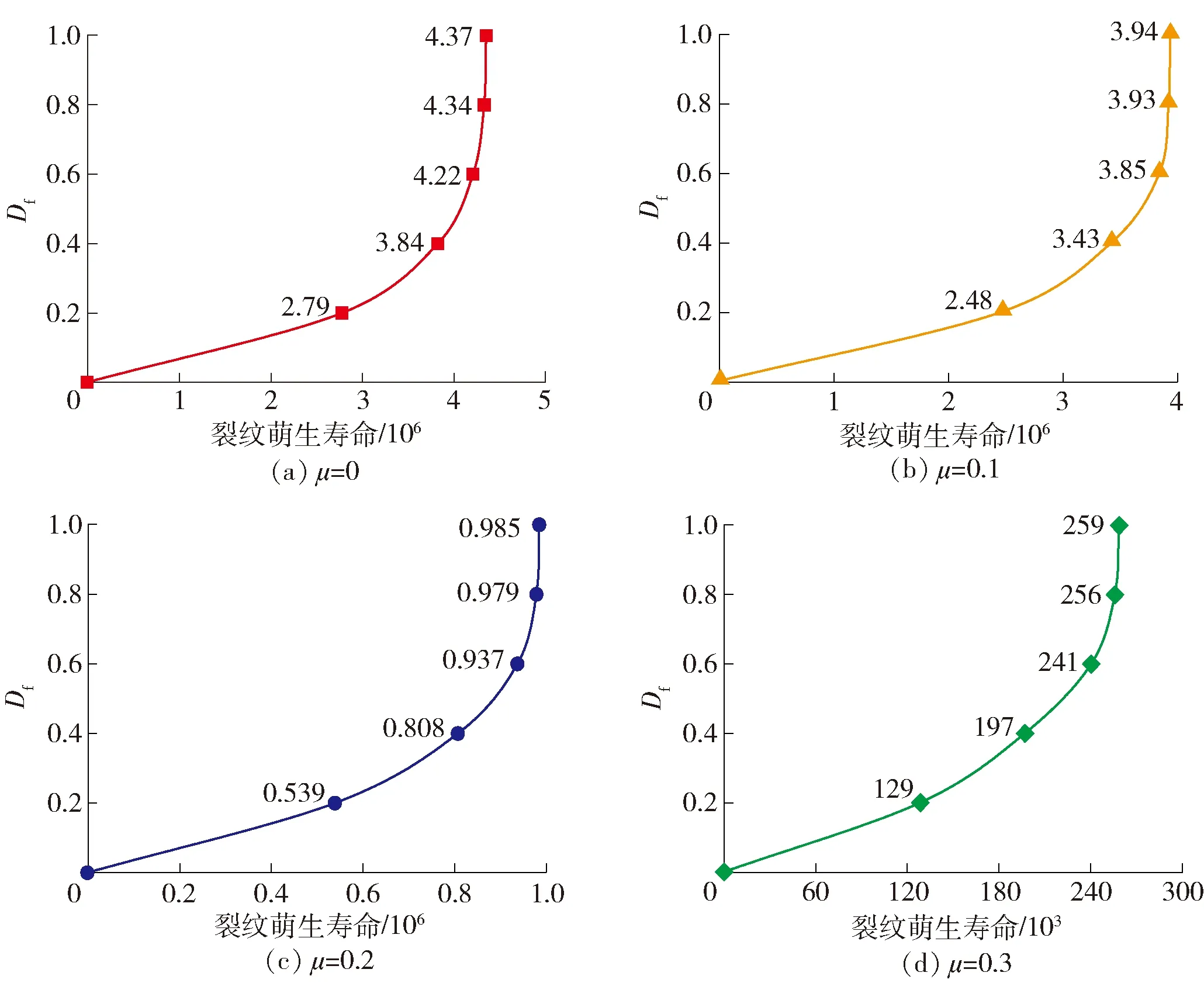
双馈型风力发电机是风电市场的主流机型，其增速箱一般由行星轮系和平行轮系组合而成.其中，处于高速级的平行轮系承受高频交变应力，因此在风电传动系统中最易发生疲劳失效.本文的研究对象，即为FD70A风电机组的高速级传动齿轮，该机组参数如表1所示[29].其中，切入风速、额定风速和切出风速分别为v切入=3 m/s，v额定=13 m/s、v切出=25 m/s，机组额定功率P额定=1.5 MW.当风速过小(v

表1 FD70风电机组的主要参数

根据空气动力学经典理论，叶片的输出功率[29]为

(10)

式中：P为风力发电机叶轮输出功率；Cp为风能利用系数；ρ为空气密度；R为叶轮半径；v为额定风速.

根据风力发电机的工作特性，在风力作用下，增速箱的输入转矩，可采用分段函数表示为

(11)

式中：T额定=9 550P额定/n，为额定输入转矩，n=15 r/min；v为实际风速.

可见，本文只需讨论2种风速工况，即v切入≤v

本文的介观尺度模型，是从晶粒层面描述齿轮的承载特性，模型加载的边界条件实际是齿面啮合时的接触载荷.因此，将齿轮轮齿在任意时刻的啮合接触，简化为2个曲率半径不同的可变形圆的相互接触.同时，由于接触宽度远远小于齿面的曲率半径，因此，齿面啮合过程可进一步等效为一个刚性圆在无限弹性平面上的滚动接触，如图5(b)所示，其中等效后圆的曲率R由公式1/R=1/R1+1/R2求得.

图5 齿面接触的简化模型

根据赫兹弹性接触理论，得到齿面的接触区宽度

(12)

式中：Fn1=2T/d1，代表齿轮传递的法向载荷(根据式(11)的叶轮转矩与增速箱传动比，计算可得)，d1为主动轮的分度圆直径；L为齿厚；R1、R2分别为主、从动轮的曲率半径；E1、E2分别为主、从动轮的弹性模量；μ为材料泊松比.

在此基础上，利用σ=2Fn1/(πbL)可获得啮合区内的法向接触应力.在v1、v2两种风况下，高速级齿轮齿面啮合区的计算结果如表2所示.

表2 不同风速的齿面接触区计算结果

2.2 介观模型的移动加载策略

本文利用移动加载方式，模拟齿轮之间的滚动接触效应.考虑到赫兹接触的特点，接触区内的应力分布如图6(a)所示，即分布形式为

(13)

式中：P(x)为法向应力分布函数；Pmax为最大赫兹接触应力；x为载荷加载的位置；xc为最大载荷对应的位置；a为载荷接触半宽.该接触应力分布曲线已做归一化处理.

考虑齿间摩擦因数，获得接触区内的切向应力

Q(x)=μ·P(x)

(14)

式中：Q(x)为切向应力分布函数；μ为摩擦因数.

由于2种风况下的接触区大小不同(见表2)，计算模型需要满足2种移动加载的要求.因此，考虑高风速对应的接触区较宽(1.45 mm)，本文最终建立10 mm×5 mm的介观仿真模型，如图6所示，其中晶粒内部的单元类型为CPE3，晶界为COH2D4内聚力单元.P(x)、Q(x)分别为齿面的法向与切向接触载荷，二者沿图中箭头方向进行移动，每一次加载循环，移动距离为(3+b) mm, (b为前文赫兹接触宽度).图中所示的3 mm×2 mm矩形区域是本文研究的重点，亦即发生疲劳损伤的潜在区域.

图6 介观模型的建模思路

风电齿轮的材料为42CrMo，其基本的性能参数为：弹性模量E=210 GPa，泊松比μ=0.3，断裂韧性KIC=61 MPa·m1/2，抗拉强度σb=1 080 MPa.在此基础上，可以分别确定晶粒与晶界的性能参数，即晶粒内部参数与宏观性能参数相同，而晶界的内聚力单元则需要单独考虑.

内聚力单元的法向弹性模量Enn=210 GPa，由Ess=Ett=Enn/(2(1+μ))可知，切向弹性模量Ess=Ett=80 769 MPa；初始临界牵引力t0=980 MPa.除此之外，在内聚力单元的损伤判据中，临界断裂能也是很重要的一个参数，其计算方法为

(15)

基于上述分析，本文介观仿真模型的材料参数，汇总后如表3所示.

表3 介观模型的材料参数

为了保证模拟结果的准确性，并提高仿真效率，在模拟前需要确定合适的网格密度.本文选择网格参数为0.7～1.4，建立了8种密度的介观模型，赋予表3的材料参数.分别施加赫兹移动载荷，提取各网格参数下的网格数量、Mises等效应力及S12剪应力数值，结果如表4所示.为了便于观察网格参数对模拟结果的影响，表4数据绘成曲线如图7所示.可见，当网格参数控制在1.0(单元尺寸为0.020 mm)以内时，Mises应力和S12应力值趋于定值，网格的进一步细化对结果已无实质影响，因此，可将1.0认定为网格参数的临界值.综合考虑计算成本，本文模型最终的网格参数设定为1.0，即网格尺寸设定为0.02 mm.

表4 不同网格参数下的网格数量及应力计算结果

图7 不同网格参数下的网格数量及应力趋势

2.3 疲劳损伤演化的分析策略

在疲劳损伤理论中，最著名也最易于实现工程化的，是Miner线性损伤累积理论.在大量的试验数据支撑下，该理论获得了广泛应用，并且使疲劳损伤的数值仿真成为可能.因此，Lemaitre等[30]提出了周期跳跃加载方法，其原理如图8所示.可见，疲劳损伤演化的过程，可以划分成若干个循环块(ΔN)，在每个循环块内部，损伤程度与应力循环次数成正比.

图8 周期跳跃加载方法

因此，本文风电齿轮的疲劳演化分析策略如下.

1) 针对材料的损伤因子变化区间[0,1]，划分为若干个循环块，本文取ΔD=0.2，即把整个损伤过程分成5个循环块(循环变量i=1，2，…，5).

2) 针对第i个循环块，移动边界载荷P(x)和Q(x)，计算该循环块内的应力- 应变场，参照Jiang等[31]提出的疲劳断裂准则，计算疲劳参数

(16)

式中：Δε为法向应变范围；σmax为最大法向应力；Δγ为剪切应变范围；Δτ为剪切力范围；J为材料参数，由拉扭试验获得，本文中J=0.3.

3) 基于Fp与疲劳寿命之间的关系式(Fp-Fp0)mNf=C，结合线性疲劳损伤累积准则，计算疲劳损伤的演化速率

(17)

式中：Nf代表单元疲劳寿命；Fp0、m、C均为材料参数，其数值分别为：Fp0=0.5，m=2，C=1.5×106.

4) 确定第i个循环块对应的应力循环次数，即ΔN=ΔD/(dDf/dN).

5) 计算每个内聚力单元实际发生的损伤值，根据式(7)～(9)更新单元力学性能参数，亦即将ΔN次循环后的损伤值累加到计算模型.

6) 计算第i+1循环块的损伤演化过程，直至损伤因子D=1.

7) 将各个循环块对应的应力循环次数累加，即为疲劳损伤寿命.

需要指出的是，在有限元仿真过程中，每个单元获得的Fp和dD/dN都不同，因此在第4)步计算中，疲劳损伤的演化率需要带入所有单元中的最大值.仿真的具体流程如图9所示.

图9 疲劳损伤演化的仿真流程

3 疲劳演化的仿真结果

3.1 演化进程分析

如表2所示，不同风速对于介观模型而言，仅仅影响模型表面的接触载荷及接触区宽度.在相同的损伤判据下，外部载荷将影响疲劳参数Fp以及损伤演化速率dD/dN的数值，但模型内部的缺陷萌生机制相同.因此，本文仅以5.5 m/s的低风速工况为代表，研究损伤位置与扩展趋势预测.模型表面的最大法向接触载荷Pmax=862 MPa，接触区宽度b=0.6 mm，载荷移动距离3.6 mm.

为了研究损伤形成以后的扩展趋势，在第1个计算流程的5个循环块全部结束以后，并未如图9所示终止仿真，而是在此基础上，继续计算1个加载周期(即5个循环块，每个循环块ΔD=0.2).图10为第1个加载周期结束后的仿真结果，图中左侧彩色云图为S12剪切应力，右侧为缺陷萌生与扩展的示意图.可见，模型中最初的2条裂纹缺陷出现在距模型表面0.13和0.27 mm的位置.图10(b)为第1加载周期结束时的缺陷状态，相对图10(a)的损伤状态，已经有所扩展.

图10 第1加载周期裂纹萌生与扩展

图11为第2加载周期各个循环块的计算结果，同样，左侧为剪应力分布云图，右侧为缺陷扩展轨迹图.可见，随着循环次数的不断增加，裂纹从图10(a)的次表层位置，逐渐向深度方向和水平方向同时扩展，并最终结成网状.而且，缺陷的扩展是沿着晶界进行的，同时伴随着明显的应力集中现象.

3.2 实验验证

由于缺陷在第2加载周期的扩展趋势更为明显，因此本文将该周期内各个循环块结束时的裂纹轨迹图提取出来.如图12所示，裂纹的扩展方向带有很强的随机性，但是由图12(d)与图12(e)的对比可见，裂纹首先沿表面平行的方向结成网状，然后再向深度方向继续扩展，这与经典的剥落损伤形成过程完全吻合.图13为Beynon等[32]通过滚动接触疲劳实验，获得的金属材料剥落区显微照片，首先网状结构清晰可见，另外，疲劳裂纹明显在次表层的深度比较大，说明在循环载荷作用下，裂纹源从次表层开始萌生，并最终扩展形成网状.

图13 滚动接触剥落实验显微照片[32]

本文仿真的疲劳裂纹轨迹图，与实验观测的剥落区形貌高度一致，表明前述介观尺度模型合理、有效，并可用于后续的仿真分析.

4 风电齿轮的疲劳寿命分析

在完成疲劳损伤演化的仿真基础上，将各个循环块的应力循环次数(即ΔN)进行累加统计，即可得到计算模型的疲劳寿命.众多研究学者[33]结合现有无损探伤和裂纹扩展模型的适用范围，将裂纹尺寸小于0.3 mm定义为裂纹萌生阶段、裂纹尺寸在0.3～1.0 mm定义为短裂纹扩展阶段、裂纹尺寸大于1.0 mm定义为长裂纹扩展阶段，因此，本文将裂纹尺寸小于1.0 mm的情况，定义为介观尺度的微裂纹萌生阶段；当裂纹尺寸大于1.0 mm时，定义为宏观尺度的裂纹扩展阶段，即可进行断裂及模拟.从图10、11裂纹扩展的局部放大图可看出，在裂纹萌生及扩展的损伤演化过程中，扩展的尺寸保持在1 mm以内，可视为微裂纹的萌生阶段，故本文将该尺度下损伤演化的寿命定义为裂纹萌生寿命N.

4.1 不同风速下的裂纹萌生寿命

针对5.5和13.0 m/s两种风况，模型表面施加的法向移动载荷最大值分别为862和2 114 MPa，接触区宽度分别为0.60和1.45 mm，载荷移动距离分别为3.60和4.45 mm.

图14为2种风况下裂纹萌生寿命预测曲线，表5为各个阶段的寿命统计结果.由表5和图14的对比可见，风电齿轮在啮合过程中，从无损状态累积到损伤变量Df=0.2，所需要的循环次数较其他阶段更多，Df从0到0.4的寿命约占裂纹萌生寿命的75%.随着Df值的不断累积，材料的损伤速率(即曲线瞬时斜率)逐渐加快.此外，2种风速工况下，齿轮的裂纹萌生寿命相差2个数量级.由此可以推断，高风速所对应的高接触应力，严重影响齿轮的滚动接触疲劳寿命.如果风力机在风能资源丰富的地区工作，则需采取必要的工艺措施，防止齿面过早失效.

图14 不同风速下裂纹萌生寿命曲线

表5 不同风速下裂纹萌生寿命结果统计

4.2 不同润滑状态下的裂纹萌生寿命

齿面接触常处于不同的润滑状态，此处仍以5.5 m/s的低风速工况为例，讨论无摩擦，以及摩擦因数分别为0.1、0.2、0.3时的仿真结果，图15为不同摩擦因数下，疲劳损伤处于不同演化阶段的裂纹萌生寿命曲线，表6为不同摩擦因数下的裂纹萌生寿命统计结果.

图15 不同摩擦因数下裂纹萌生寿命曲线

表6 不同摩擦因数下裂纹萌生寿命结果统计

可见，4组曲线中，损伤演化的速率均是随损伤程度的增加而加快，其中，损伤累积量Df从0积累到0.2所占比例最高；Df为0～0.4阶段的寿命占裂纹萌生寿命的75%～85%，其寿命曲线斜率在Df为0～0.5范围内较小.随着摩擦因数的增大，该阶段在整个疲劳寿命中的占比逐渐缩小，即增大摩擦因数将加快损伤演化的进程.此外，还存在一个明显的趋势：摩擦因数值对齿轮的裂纹萌生寿命有显著影响，例如摩擦因数为0.3的疲劳寿命与摩擦因数为0.1相差一个数量级.由此可知，齿间润滑不良将大大降低齿轮的裂纹萌生寿命.