“一题多变”在小学数学解题教学中的运用研究

◎黄玉兰

(福州市鼓山新区小学，福建 福州 350011)

新课程标准要求小学数学教学要有现实意义，引导学生掌握科学的数学学习方法，培养学生的创造性思维.这就要求学生具备一定的研究能力和自主学习能力，并真正参与学习和实践活动，观察、发现和自主验证数学公式推导过程等.这也就要求教师在进行相关数学问题的讲解时利用“一题多变”的教学策略，引导学生在掌握数学问题基本解法的基础上进行更深入的创新和思考，在激发学生数学学习兴趣的同时提升学生的数学解题能力和逻辑思维能力.

一、“一题多变”的含义和作用

从本质上讲，“一题多变”是指在不改变原有问题本质的前提下，变化题目中的相关条件、问题或情境等，由一个题目变化出多个题目的教学方式，通过对问题进行有效开阔和深化，让学生在学习基础知识的同时有效拓宽视野，并深刻理解相关类型题目.

“一题多变”教学策略的运用会让学生觉得耳目一新，对旧知产生新的兴趣，产生求知欲，进而积极主动地探求问题的答案.“一题多变”教学策略的运用会让学生的数学思维变得更加活跃，打破思维定式.“一题多变”教学策略的运用还可以有效帮助学生深化对相关知识和题目的理解，更加熟练地掌握相关数学问题的解题技巧，进而提高对相关数学知识触类旁通的能力.“一题多变”教学策略不仅能有效提升数学课堂教学效率，还能为学生的终身学习奠定基础.

二、“一题多变”的运用原则

对于“一题多变”在数学解题教学中的实际应用，教师应遵循以下原则.

(一)普遍运用原则

由于小学生的年龄比较小，在实际学习中，他们集中注意力的时间是有限的，对事物的认知也是非常有限的.所以，为了满足学生在数学学习上的实际需求，教师要不断根据学生的实际情况进行必要的探索，对教材内容进行深入拓展，挖掘“一题多变”的相关素材，将“一题多变”教学策略普遍运用于数学课堂中，从而增加课堂教学的趣味性，培养学生的创新意识.并且，教师应通过一系列相关数学题目的讲解使学生领悟相关数学题目的实质，使学生理解复杂的难题，增强学生学习数学的信心和兴趣.不管是新授课、练习课还是复习课，教师都可以采用“一题多变”教学策略，让学生在实践、模仿中不断创新，不断提高观察、分析、解决问题的能力，提高思维的深刻性和创新性.

(二)循序渐进原则

数学的学习过程是循序渐进的.在学生学习新知识之后，教师要利用“一题多变”进行相关知识的拓展和迁移，协助学生构建自己的学习体系，提升学生的数学思维能力.在利用“一题多变”教授数学知识的同时，教师需要根据学生的实际接受能力和理解能力对学生进行引导，让学生能够由浅入深、由简到繁、由具体到抽象地进行变式，进而激发学生的学习兴趣.教师要注意不能一下子将难度提得过高，否则会让学生对数学这门学科产生抵触情绪，从而降低学生的学习效率.教师可以先设置一些符合学生接受能力的变式题，然后逐步增加难度，形成有梯度的变式题组，让学生在顺畅解题的同时主动巩固原有的数学知识，锻炼数学思维能力.

(三)量力性原则

将一个问题从不同角度以不同方式进行变化，问题可能会变得更简单，也可能会变得更复杂.如果教师给出的变式过难，那么可能只有少数优秀学生可以解答，大多数学生只能看着问题无从下手，这会导致教学成效降低.因此，教师在进行“一题多变”教学的时候要遵循量力性原则，不要一味追求难度变化，而要根据教学内容和学生的实际情况合理控制题目的难度，以免超出学生的能力范围而导致学生陷入“题海”，造成事倍功半、事与愿违的结果.

要想做到量力而为，就要注意以下三点.一是在学生掌握基础知识后再进行问题变换，否则，学生的思维可能会在变换中混乱，适得其反.二是对问题变换提出具体、明确的要求，控制问题变换的难度.例如，明确提出问题的哪一部分要改变、改变问题的方式、解决问题的步骤等.三是选择符合学生能力水平的问题.对于超出学生能力水平的问题，教师不应让全班同学在课堂上回答，可让学有余力的学生在课后讨论和解题.

(四)以学生为主体原则

教学过程应是以学生为主体、以教师为主导、师生互动的过程.教师不应以灌输知识为主而使学生处于被动接受的状态，这会影响学生学习的积极性和主动性，不利于学生思维能力的培养.教师应采取各种手段，了解学生的学习需求，给学生提供自主探究与合作交流的机会，让每名学生都能展示自己，从而不断体会到成功的喜悦.

三、“一题多变”在小学数学解题教学中的运用策略

(一)利用“一题多变”，将新题变成旧题

由于年龄小，一些学生不能马上就认识到知识的本质.在实际教学中，如果学生遇到解题障碍，教师可以引导学生思考能不能将相关数学题目变成之前学过的类似题目，通过改变数据或条件等将一些不常见的知识变成比较熟悉的知识，以旧导新，达到有效解题的目的.

例如，人教版数学六年级上册《分数除法》单元有这样一道练习题：某商店销售矿泉水，进货时5元钱4瓶，售出时5元钱3瓶，要获利300元，需售出多少瓶矿泉水？

一些学生习惯性地认为物品总价的数据要比数量的数据大，解题的时候就很容易遇到障碍.这时，教师可以引导学生修改一下价格，把题目变为：某商店销售矿泉水，进货时12元钱4瓶，售出时12元钱3瓶，要获利300元，需售出多少瓶矿泉水？

通过解答变式题，学生马上就会发现这道题实际上是三年级时所学的“包含除”，先用“12÷3-12÷4”求出单瓶的成本价与售价差是1元，再用获利总价除以单瓶获利的价格(300÷1)求出商店需售出多少瓶矿泉水.回到原题，题干中价格的数据比较小，计算单价时会出现分数，实际上解题思路是一样的.教师通过数据的变化，将新题变成旧题，既使难题迎刃而解，又培养了学生举一反三、灵活转换的解题能力.

(二)利用“一题多变”，触类旁通

在实际教学中，教师可以引导学生用联系的思维去看待不同的数学问题，在“变”中建立不同问题的联系.这样做既能帮助学生有效巩固相关解题方法，又能使学生感受到“一题多变”中以不变应万变的解题本质.

例如这道小数简便计算题：3.6×4.2+64×0.42.刚看到题目时，学生可能无从下手.教师可引导学生将64×0.42变成6.4×4.2或将3.6×4.2变成36×0.42.这样学生就能运用乘法分配律进行计算.在解答后，教师可为学生再出一些类似的题目，并让学生利用对比分析和讨论的方式自觉总结这类题目的计算方法.当学生总结出计算方法之后，教师要利用“一题多变”引导学生进行相关数学知识的拓展，让学生思考：整数和分数的简便计算中，有没有类似的规律？学生利用小组讨论、举例验证等方式自主思考，发现原来整数、分数、小数混合简便运算中也有这样的规律.此时，学生实现了知识的融会贯通、触类旁通.

所以，在解决各类数学问题的时候，教师要引导学生对相关题目的内容形式、已知条件等做深入探讨，掌握相关题目反映出的数学本质；要求学生对一道普通的数学题目进行“一题多变”，从变化中自主寻找解题方式，发现解题规律，有效提升自己的数学综合能力.

(三)利用“一题多变”，打破思维定式

在日常的解题教学中，教师还可以通过改变学生熟悉的数学问题的提问方式实现“一题多变”，鼓励学生积极思考，在变中求进、进中求通，进而打破思维定式，拓展自己的创新思维空间，提升思维的灵活性.

例如，六年级上册《百分数》单元有这样一道题：某商场进了两只玩具泰迪熊，均以80元的价格销售.临近春节，两只玩具泰迪熊均涨价20%，售出了一只;两个月后，另一只玩具泰迪熊在此基础上降价20%售出.该商场销售这两只玩具泰迪熊是赚了还是亏了？

解题步骤是:(1)计算第一只玩具泰迪熊的售价，即80×(1+20%)=80×120%=96(元);(2)计算第二只玩具泰迪熊的售价，即96×(1-20%)=96×80%=76.8 (元);(3)计算该商场销售两只玩具泰迪熊的盈亏，即(96+76.8)-(80×2)=12.8(元).答案是赚了12.8元.

在“一题多变”的过程中，教师可将问题改为：某商场以每只600元的售价同时售出两只玩具泰迪熊，一只亏了25%，另一只赚了25%，该商店售出这两只玩具泰迪熊是赚了还是亏了？

解题步骤是:(1)计算亏的那只玩具泰迪熊的进价，即600÷(1-25%)=800 (元);(2)计算赚的那只玩具泰迪熊的进价,即600÷(1+25%)=480(元);(3)计算该商场销售两只玩具泰迪熊的盈亏，即(800+480)-(600+600)=80(元).答案是赚了80元.

学生往往会误以为两道题的解法是一样的，但其实第一道题探讨的是现价和原价之间的关系，而且属于单位“1”已知的题型，而第二道题探讨的是进价和售价之间的关系，而且属于单位“1”未知的题型.通过这两道题的教学，教师不仅帮学生厘清了现价和原价、进价和售价之间的联系和区别，又有效帮助学生打破思维定式，提高学生分析问题、解决问题的能力，拓展了学生的数学思维.

又如六年级上册《圆》单元的这道练习题：王大爷用37.68米长的篱笆在房前的空地上围了一个圆形鸡舍，现在由于养鸡数量增加，他利用一面墙和原有的篱笆将鸡舍改成了半圆形，改变后鸡舍的面积增加了吗？如果增加了，增加了多少？

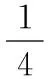
学生做惯的题型是靠一面墙围篱笆，而现在变成靠两面墙围篱笆，鸡舍的周长、半径和面积再次发生变化，但圆的周长和面积计算公式没变.这样的变式不仅使学生对圆的面积和周长的相关知识运用得更加纯熟，也使学生思维的灵活性得到了提高.

(四)利用“一题多变”，形成解题模块

在实际进行“一题多变”的时候，教师可以这样变：(1)变条件，增加多余条件、干扰条件或复杂条件；(2)变问题，条件不增加，提出不同的问题；(3)逆向思维，变问题为条件，变条件为问题；(4)给出一些条件和结论，组成辨析题组；等等.不同的变化从不同的角度锻炼学生的数学思维和解题能力，从而使学生灵活运用所学.

例如这道分数除法解决问题：一个班级有男生30人，女生24人，男生人数是女生的几倍？女生人数占男生人数的几分之几？教师可以在这道题目的基础上向学生提出更多问题，如：男生人数占全班人数的几分之几？女生人数占全班人数的几分之几？男生人数比女生人数多几分之几？女生人数比男生人数少几分之几？男生人数比女生人数多的部分占全班人数的几分之几？女生人数比男生人数少的部分占全班人数的几分之几？通过不断变换角度发问，学生不停地跟着问题积极思考，寻找解决问题的方法，从而对知识理解得更加透彻.

在实际教学中，类似的教学案例是非常多的，这就需要教师在实际教学中不断总结和归纳，弄清数学问题的内涵和外延，并进行合理分类，在变中寻求不变，形成分学段、分单元、分类型的解题模块，使学生在解题时由一个知识点联想到多个知识点，以一题的解答达到多题的学习效果，进而提升学生思维的深刻性、广阔性和创新性.

四、结束语

综上所述，“一题多变”这样的教学形式和教学方法可以有效培养学生的逻辑思维，协助学生构建自己的数学知识体系，让学生发现学习数学的乐趣，进而强化学生学习数学的积极性.因此，小学数学教师要积极探索“一题多变”在实际教学中的应用方式，不断提升自身的综合素养和教学水平，从而促进小学数学教学的高质量发展.