固溶Ce对α-Fe力学性能影响的机理研究*

2022-09-08刘香军杨昌桥任慧平杨吉春金自力

功能材料 2022年8期

刘香军，杨昌桥，任慧平,2，杨吉春，金自力,2

(1. 内蒙古科技大学材料与冶金学院，内蒙古包头 014010；2. 内蒙古自治区新金属材料重点实验室，内蒙古包头 014010)

0 引言

添加微量稀土便可显著提升钢材的综合性能[1]。Zang等[2]研究显示，在20Cr13马氏体不锈钢中添加0.02%(质量分数) Y后试验钢的抗拉强度提高了330 MPa，归因于Y对钢中夹杂物的改性作用。但石晓霞等[3]指出，Ce对10Cr5MoV钢强度的贡献值不大，Ce含量为0.0015 %(质量分数)时，0 ℃冲击韧性提高了30 J，试验钢延展性得到明显改善。当前不乏稀土能够提高钢材抗拉强度、硬度、塑韧性、耐磨性等力学性能的报道，也获得了一些有意义的实验结论，但报道多是以稀土元素变性夹杂物为视角去分析稀土对钢力学性能的影响，且以实验研究为主，理论研究较少。另一方面，随着洁净钢冶炼技术的不断进步，钢中氧硫等杂质含量进一步降低，取得了诸如汽车板(T.O<30×10-6)、高端轴承钢(T.O<5×10-6)、帘线钢(T.O<15×10-6)等一批高洁净度钢种[4]，目前国内外先进钢厂洁净钢冶炼水平已达W(C+T.O+N+P+S+H)≤100×10-6，钢中夹杂物数量显著降低，传统的夹杂物控制和应用研究应及时转变思路[5]。

稀土在洁净钢中的应用除变性夹杂物外其作为微合金元素的应用应投入更多的关注，掌握稀土在钢中的固溶行为是探究稀土微合金化作用的先决条件。由于稀土元素的原子半径约是铁原子的1.5倍，其在钢中的固溶度极低，稀土在钢中只能形成溶解度极低的端际固溶体[6]。戢景文等[7]通过研究Fe-P-La、Fe-P-La-N、Fe-C-La等合金体系的内耗峰，从原子尺度上证实了稀土元素能够以固溶态存在于铁及铁合金中，这为稀土元素在钢中的合金化作用提供了有力的理论依据。然而稀土固溶量很低[8-9]，给实验研究带来了极大的困难，现有的检测设备和常规的微区分析方法都很难对低级固溶量的稀土进行准确表征，同时也很难避免实验过程中的非实验因素。

针对传统实验研究效果不理想的现状，开展模拟计算研究将是一条有效的捷径。本文采用第一性原理计算方法研究稀土Ce原子在α-Fe中的占位倾向、揭示Ce在钢中的固溶行为、分析其固溶机理、并分析Ce对α-Fe力学性能的影响，以期补充并丰富稀土元素微合金化作用机制的微观认识。

1 计算方法与模型

本文基于密度泛函理论采用VASP(ViennaAb-initioSimulation Package)软件计算Fe-Ce体系的热稳定性、力学性质和电子结构等。计算中，价电子与离子间的交互作用选择投影缀加波方法PAW(Projector Augmented Wave)，电子间的交换关联相互作用采用广义梯度近似GGA(General Gradient Approximation)中的PBE(Perdew-Burke-Ernzerh)泛函形式[10]，平面波截止能为450 eV，布里渊区积分计算使用4×4×4的MP-k(Monhkorst-Pack)型的k网格[11]，自洽循环能量收敛设置为1.0×10-6eV/atom，力收敛为0.02 eV/0.1 nm，并且掺杂体系考虑了磁性，通过优化得到晶胞参数以及体系能量，所有计算由VASP程序完成。

对单胞α-Fe结构进行优化计算可得其体相特性，其中晶格常数a(0.283 nm)，体积模量B(176 GPa)，磁矩M(2.25 μB)和内聚能Ecoh(5.06 eV/atom)，如表1所示。从表1可以看出，本次计算结果与文献记载的他人计算结果及实验值基本一致，表明选用的计算方法及设置的参数是合理有效的。一般来说，原子半径较大的外来原子倾向于占据取代位置，而原子半径较小的外来原子更倾向于占据超胞中的八面体间隙或者四面体间隙位置[16]。Ce原子半径为0.270 nm，远大于Fe(0.172 nm)的原子半径，因此判断，Ce应优先取代超胞中的Fe原子，而非以间隙固溶的方式存在于Fe基体中，这与杨等[17]研究结果一致。本文构建4×4×4的α-Fe超晶胞模型，超晶胞中有128个原子，将Ce取代1个Fe原子，如图1所示。

表1 α-Fe平衡晶格常数a, 体积模量B, 磁矩M, 内聚能Ecoh.

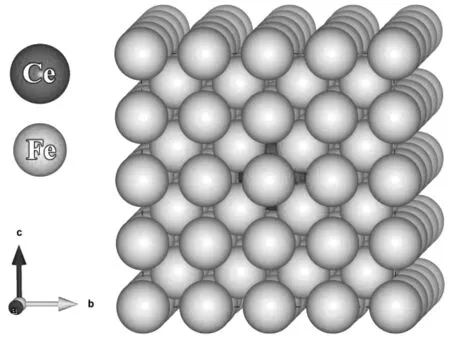
图1 Fe-Ce晶体结构

为判断Ce能否在α-Fe中固溶，本文引入溶解能，溶解能的计算公式如下[18]：

(1)

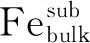
溶解能为负值时，表示晶胞结构可以稳定存在，反之，晶胞结构不能稳定存在。计算Fe-Ce掺杂体系溶解能为-3.75 eV，表明掺杂体系可以稳定存在，即Ce能够取代Fe原子固溶在α-Fe中。

2 结果与讨论

2.1 Ce对α-Fe体系力学性能的影响

2.1.1 弹性常数

体系能否稳定存在，需考虑以下两个因素：(1)热力学上要稳定，即上节讨论的溶解能；(2)晶格的动态平衡，即晶格的力学稳定性。不同晶系的晶体具有不同的独立弹性常数，α-Fe-Ce掺杂体系为立方晶系，对于立方晶系来说，由于对称关系，具有3个独立的弹性常数(C11, C12, C44)。

晶格的力学稳定性可由Born-Huang判据进行判断[18]，Fe-Ce晶体结构的独立弹性常数C11、C12和C44须同时满足式(2)[19]，晶体才能稳定存在。

C11>0, C44>0, C11+2C12>0, C11>C12

(2)

Fe及Fe-Ce掺杂体系弹性常数的计算结果如图3所示。将弹性常数带入式(3)进行验证，结果表明，Fe-Ce掺杂体系满足Born-Huang力学稳定性判据，因此，Fe-Ce掺杂体系满足弹性稳定机制，晶体结构稳定，这与溶解能分析结果一致。

弹性常数C11和C33分别表示固体材料在X轴和Z轴方向上的不可压缩性[20]，在立方结构中，C33等于C11。从图3可以看出，体系中的C11数值都较C12、C44大，表明Fe-Ce掺杂体系在单轴条件下，X轴和Z轴两个方向均不容易被压缩。C44可用于表征晶体在(100)面上抵抗剪切应变的能力[21]。从图2可以看出，Ce掺杂后体系的C44值减小了，由98.87 GPa减小为94.31 GPa，说明Ce的掺杂降低了体系的抗剪切应变的能力。

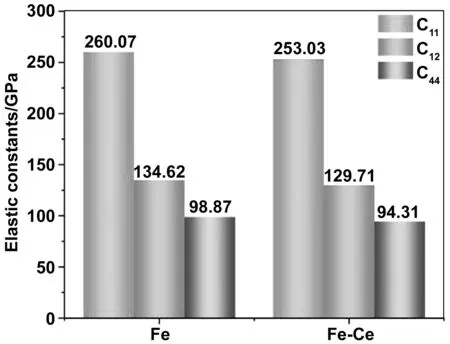
图2 纯Fe及Fe-Ce掺杂体系的弹性常数

2.1.2 弹性模量及维氏硬度

弹性模量是描述晶体材料弹性的物理量，不同的受力情况，可分为体积模量B、剪切模量G和杨氏模量E，可依据弹性常数由Voigt-Reuss-Hill近似算法计算，计算公式如下[22-23]：

(3)

(4)

对于立方晶系，BV、BR、GV、GR可由下式计算：

(5)

(6)

(7)

(8)

式中，下标H、V、R分别代表Hill、Voigt和Reuss近似。

体积模量可表征均质各向同性固体材料的弹性，反映晶格在压力条件下抵抗变形的能力[24]。一般来说，体积模量较大的固体材料具有较高的不可压缩性。剪切模量是剪切应力与剪切应变之比，反映晶体材料抵抗塑性变形能力。杨氏模量是指晶体材料在弹性变形范围内，作用于材料上的应力(如拉伸、弯曲、扭曲等)与之产生的相应应变之比，是表征晶体中原子间结合力强弱的物理量，是组织结构的不敏感参数[25]。工程上，杨氏模量常作为材料刚度的度量，表征材料变形的难易程度[26]。

Candan等[27]基于Pugh模量比(k=G/B)提出一种新的理论模型，可用于预测材料的维氏硬度HV，可用公式(10)计算。

HV=2(k2G)0.585-3

(9)

由公式(10)可看出，材料的维氏硬度与剪切模量和体积模量密切相关，其中剪切模量占比较大，这与硬度测量的实际相吻合(硬度测量值与压痕深度密切相关，而剪切模量对压痕阻力的恢复起主要作用)。

图3为纯Fe、Fe-Ce掺杂体系体积模量、剪切模量、杨氏模量和维氏硬度的计算结果。掺杂Ce后，Fe-Ce掺杂体系的B、G、E、Hv分别为170.82、79.56、206.59、7.58 GPa，较纯Fe体系分别降低了5.62、4.85、11.82、0.35 GPa，即Ce略微降低了体系的不可压缩性、抵抗剪切变形的能力、刚度以及维氏硬度，其中不可压缩性和抗剪切变形能力的分析结果与上节弹性常数的分析结果相一致。

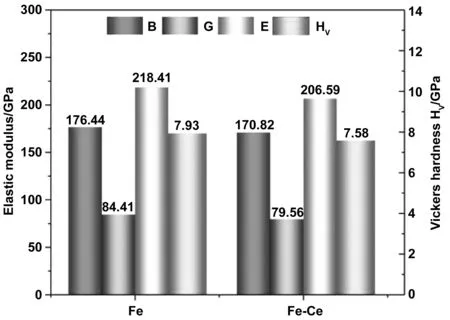
图3 纯Fe及Fe-Ce掺杂体系的体积模量B、剪切模量G、弹性模量E和维氏硬度Hv

2.1.3 韧性指标及机械加工指数

根据Pugh判据，可用B/G度量材料的韧脆性，区分韧脆性的临界值为1.75，当B/G>1.75时，该材料呈现韧性特征，反之呈现脆性特性。B/G值越大，表明材料的韧性越好[28]。泊松比σ也可用来度量材料的韧脆性，σ>0.26时，该材料表现为韧性材料，反之为脆性材料，且值越大，表明韧性越好。泊松比可由体积模量和剪切模量计算，公式如下[29]：

(10)

Sun等[30]基于弹性常数提出一种新的理论模型，用机械加工指数μM来评估金属材料的可加工性能，其值越高，表示可加工性能越好，计算公式如下：

(11)

纯Fe及Fe-Ce掺杂体系的B/G值、泊松比σ，机械加工指数μM计算结果如图4所示。由图4可见，纯Fe及Fe-Ce体系的B/G值均大于1.75、σ值均大于0.26，都呈现出韧性特征。掺杂Ce后，Fe-Ce体系的B/G值由纯Fe的2.090增大到2.147，泊松比σ由纯Fe的0.294增大到0.298，即Ce提高了体系的韧性。Fe-Ce体系的机械加工指数由1.78提高到1.81，表明Ce的掺杂改善了体系的可加工性能。

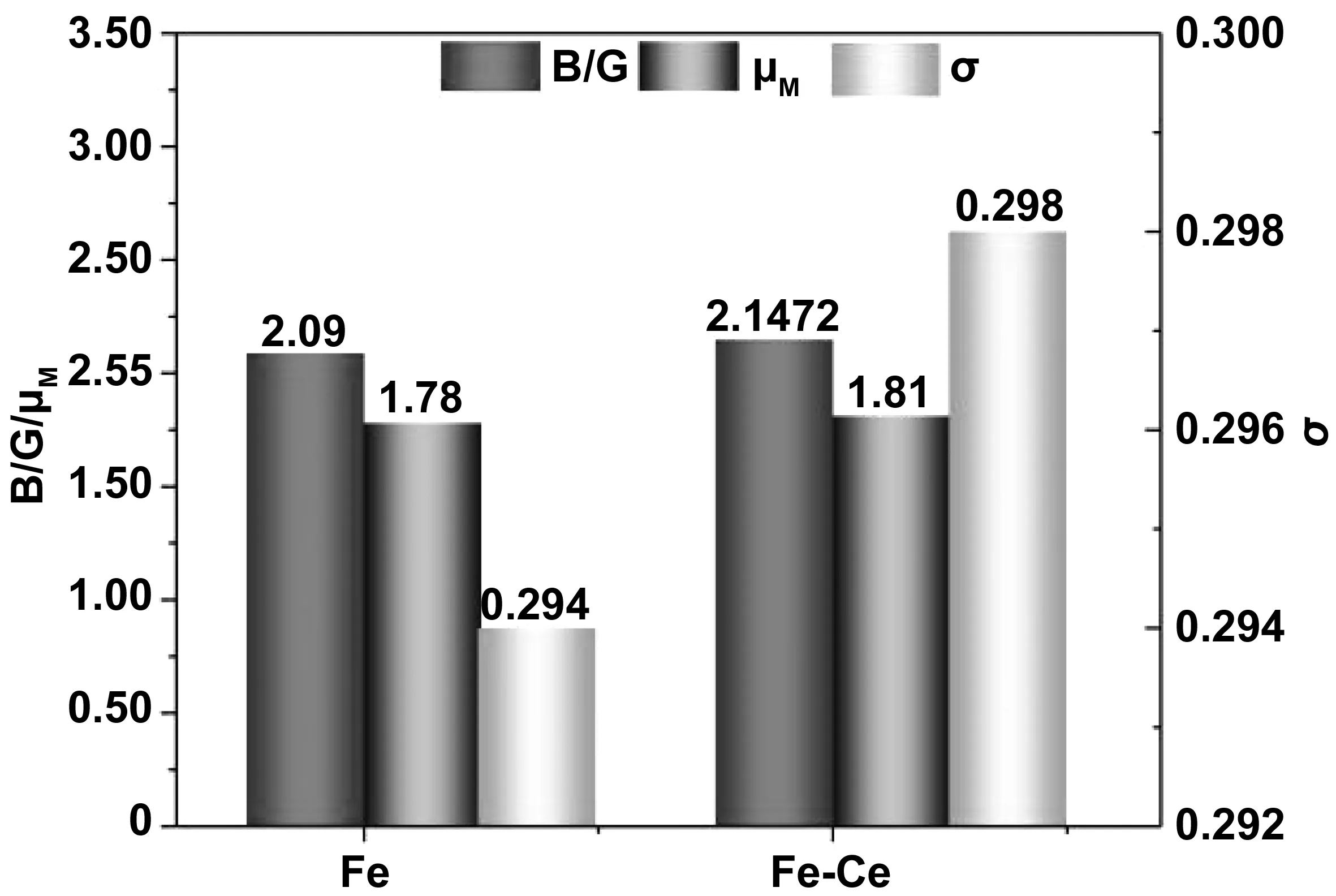
图4 纯Fe及Fe-Ce掺杂体系的B/G、泊松比σ和机械加工指数μM

基于上述弹性模量、韧性、硬度及可加工性能的分析，Ce降低了体系的不可压缩性、抗剪切变形能力、刚度以及硬度，但提高了体系的韧性和可加工性。

2.2 电子性质分析

材料的性质与其电子结构密不可分，本节试图通过几何结构、态密度、差分电荷密度、Bader电荷等来揭示Ce在α-Fe中的固溶机理以及分析Ce影响α-Fe力学性能的机制。

2.2.1 几何结构

图5为Fe及Fe-Ce掺杂体系的几何结构示意图，图5(a)为Fe晶胞(100)面示意图，图5(b)为Fe-Ce掺杂体系(100)面晶体结构示意图。掺杂Ce后，Ce原子周围的Fe原子被“挤开”，如图5(b)所示。Fe-Ce键长由优化前Fe-Fe键长的0.2832 nm增大到0.2915 nm，小于Fe与Ce原子半径之和(0.172+0.270=0.442 nm)，又因Ce原子的外层电子(4f15d16s2)对原子核封闭不严，致使Ce有较大的有效电荷，对其周围的Fe原子有较大的吸引力，因此Ce与Fe之间形成了强烈的金属键，这也是Ce能够固溶在Fe基体中的原因。

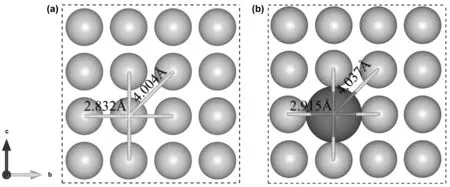
图5 (a) Fe晶胞(100)面晶体结构示意图, (b) Fe-Ce(100)面晶体结构示意图

从几何结构分析可知，Fe-Fe键长为0.2832 nm，Fe-Ce键长为0.2915 nm。根据键长越短键能越的理论，可以粗略判断Fe-Fe金属键的强度大于Fe-Ce金属键强度。在Fe-Ce掺杂体系中，同时存在Fe-Fe和Fe-Ce键，这使得整体金属键强度低于纯Fe体系，这是Fe-Ce体系的B、E、G、HV值低于纯Fe体系的主要原因。

2.2.2 态密度

总态密度(total density of states, TDOS)和分波态密度(partial density of states, PDOS)能够反映体系的键合特性，用于揭示掺杂元素Ce对体系力学性能影响的微观机制。图6(a)为Fe和Fe-Ce掺杂体系的TDOS图，图6(b)为Fe-Ce掺杂体系的PDOS(图中虚线表示费米能级)。从图6(a)可以看出，掺杂Ce后，在费米能级附近出现能级峰，说明掺杂体系具有稳定性。TDOS图中在费米能级处的态密度不为零，表明Fe-Ce体系整体上呈现出金属特性。与纯Fe体系相比，Fe-Ce掺杂体系的TDOS图中两个小的成键峰(-33.6～-33.4 eV, -17.0～-16.8 eV)分别来自于Ce-s，Ce-p轨道电子的贡献。从图6(b)可以看出，费米能级附近Fed与Cef轨道发生了杂化反应，说明Fe与Ce之间存在较强的相互作用；Fe-Ce体系的主要成键峰(-5.0～0.5 eV)是由Fed、Ced、Cef轨道电子杂化贡献的。

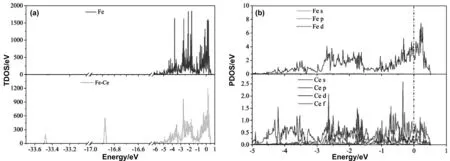
图6 (a) Fe和Fe-Ce掺杂体系的TDOS图，(b) Fe-Ce掺杂体系的PDOS图

2.2.3 差分电荷密度

差分电荷密度可更直观地观察体系中原子间的相互作用，可进一步说明成键特性，从原子尺度揭示Fe-Ce掺杂体系的强韧性机制。图7为Fe、Fe-Ce掺杂体系的电荷密度图和差分电荷密度图，标尺中的电荷密度范围为-0.01～0.005 e/(0.1nm)3，电荷密度越大，则差分电荷密度图中的区域越趋向于红色，电荷密度越小，区域越趋向蓝色。从图7(a)可以看出，Fe原子间的电荷密度均匀分布，表明纯Fe体系中Fe原子间的相互作用是金属键。在图7(b)Fe-Ce掺杂体系中，大量的电子云分布在Fe和Ce之间，且Fe得到电子，Ce失去电子。掺杂Ce后，Fe-Ce间的自由电子由Ce原子的外层价电子提供，结合几何结构分析，一个Ce原子贡献的自由电子可同时辐射作用其周围的Fe原子。由于Ce原子失去电子，Fe原子得到电子，所以Ce周围电子云密度较低，其相邻Fe原子周围电子云密度较高，Fe-Ce间的电子云密度大于Fe-Fe间的电子云密度，致使Fe-Ce掺杂体系电子云的密度较纯Fe体系大，这是Fe-Ce掺杂体系韧性(B/G、σ)高于纯Fe体系的主要原因[31]。

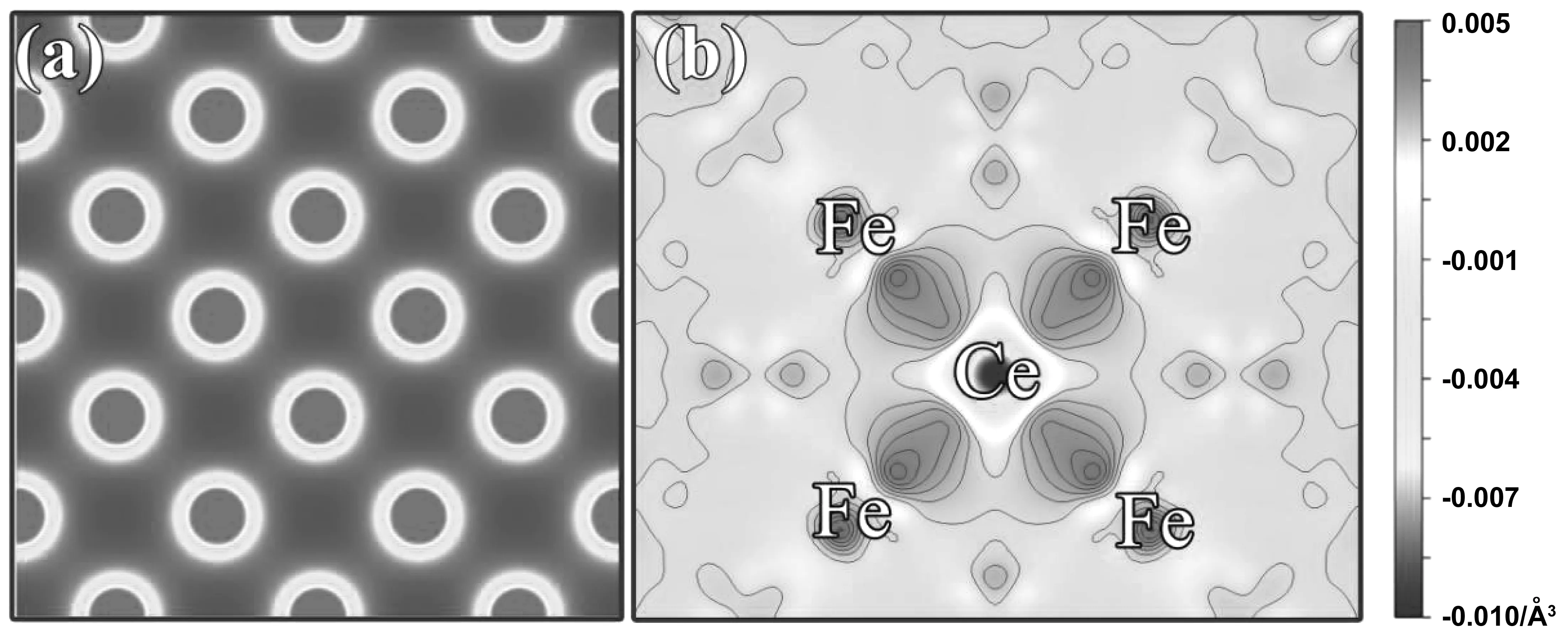
图7 Fe及Fe-Ce掺杂体系在(010)面的电荷密度及差分电荷密度图, (a) Fe, (b) Fe-Ce

2.2.4 Bader电荷

在掺杂体系中溶质元素和溶剂元素之间通常存在电荷转移，为深入了解Ce与Fe间电荷转移关系，基于Bader电荷分析方法量化了原子间电荷转移情况，掺杂体系中Ce原子、配位Fe原子的Bader电荷分析结果见表2。

表2 Fe-Ce掺杂体系中Ce原子、配位Fe原子Bader电荷

Fe1～Fe3表示与Ce最邻近的3个Fe原子。

正值表示原子失去电子，负值表示原子获得电子。体系中存在电荷转移，表明原子之间形成了相互作用关系[32]。由表2可知，Fe-Ce掺杂体系电荷转移总数为1.813，Ce原子的Bader电荷为正值(0.575)，配位Fe原子的Bader电荷均为负值，说明在Fe-Ce掺杂体系中Ce失去电子，Fe得到电子。显然，Ce与Fe之间发生了相互作用，这与态密度和差分电荷密度分析结果相一致。