COSINE多相场子通道分析程序的开发与评估

陈 林，张 昊，程以炫，郭英冉，马齐超，周帆帆，杨燕华，赵 萌

(上海交通大学 核科学与工程学院，上海 200240)

压水堆的堆芯中存在着数百个燃料组件棒束，冷却剂存在着沿棒束方向的垂直流动和燃料棒间隙的横向流动，当反应堆压力容器发生破损事故时，堆芯内可能出现剧烈相变并导致冷却剂流动剧烈波动，继而影响堆芯冷却剂的传热能力使燃料棒包壳温度骤升，并引发潜在的沸腾危机，甚至导致燃料包壳失去完整性[1]。子通道程序通过子通道模型考虑了流体在通道间的流动[2]，并通过一系列经验关系式，可以较好地预测压力容器内热工水力现象，实现对事故下反应堆的安全性能准确评估。

国际上具有代表性的子通道程序包括基于均相流或漂移流模型的COBRA-ⅢC[3]、COBRA-Ⅳ[4]、VIPRE-01[5]、THINC[6]，基于两流体六方程的VIPRE-02[7]及基于两流体八方程的COBRA-TF[8]及WCOBRA[9]等。均相流及漂移流模型忽略了相间存在的热力及流动不平衡，在低压、高流率等工况下，计算结果与实际工况具有较大差异。两流体子通道程序考虑了相间作用，实现程序对热工水力学现象良好的模拟。然而，大多数子通道程序在模拟变化剧烈的瞬态过程及强烈扰动的工况时，其计算结果往往与真实情况存在较大的差距。

国家电投集团牵头研发的一体化核电厂设计与安全分析软件包[10](COSINE)于2011年6月立项。COSINE软件包中均相流子通道程序cosSUBC[11]已经开发完成并进行了一系列测试及应用，但该程序采用了均相流模型，计算结果存在着较大的保守度，导致电厂设计的经济性较差。因此，为精确分析多相场的热工水力学现象，提高程序的计算精度，本文在COSINE均相流子通道程序的基础上，开发新的多相场子通道程序。本文首先介绍COSINE软件包中的多相场子通道程序的计算模型与求解方法，而后采用经典算例及实验数据评估程序计算的准确性。

1 多相场子通道程序的基本方程及物理模型

多相场子通道程序采用三相八方程子通道模型，将液滴相[12]进行单独考虑。程序采用控制体网格与动量网格的交错网格方法。程序中包含经验关系模型以完成方程的封闭，目前，程序采用的经验关系模型主要基于COSINE软件包[10]中自主开发的本构关系式及参考程序[13]中本构关系模型。

1.1 基本方程

1) 质量守恒方程

质量守恒方程位于控制体网格上，包括气相、连续液相、液滴相的3个连续方程。

(1)

式中：α为相份额；ρ为密度；u为轴向速度；w为间隙横向速度；x为轴向网格长度；nk为间隙数量；i代表不同相场。方程右侧1～3项分别为相变及夹带沉积、壁面换热、交混导致的各相质量变化。

2) 动量守恒方程

动量守恒方程作用于轴向和间隙动量网格中，包括气相、连续液相、液滴相共6个动量方程。

轴向动量守恒方程为：

(2)

横向动量守恒方程为：

(3)

式(2)右侧1～6项分别为压力项、重力项、壁面摩擦项、相间拖曳力项、相间传质导致动量变化项、交混导致的动量变化；式(3)右侧1～4项分别为压力项、壁面阻力项、相间拖曳力项、相间传质导致动量变化项。

3) 能量守恒方程

能量守恒方程作用于控制体网格中，程序中假定连续液相与液滴相处于热平衡态，因此将连续液相与液滴相的能量方程合并为全液相能量方程，程序中包括气相与液相2个能量守恒方程。

(4)

方程右侧1～5项分别为压力项、相间传质引发的能量变化项、相间换热项、壁面换热项、交混导致的能量变化项。

1.2 物理模型

物理模型用于封闭多相场子通道程序守恒方程，程序中包含的物理模型包括：流型图及相间作用模型、阻力模型、通道交混模型、液滴模型及壁面换热模型。

1) 流型图及相间作用模型

多相场子通道程序的相间作用模型依赖于不同的流型，程序流型图中包括泡状流、弹状流、交混流、环雾流、反环状流、反弹状流、下降液膜流，流型判别方法列于表1。相间作用模型包括相间拖曳力模型与相间换热模型。程序中认为连续液相与液滴相无直接接触，因此相间作用模型不含连续液相与液滴相的相间作用。

相间拖曳力与相间换热本构关系式分别为：

τij.i=CijρiA‴ij|uj-ui|(uj-ui)

(5)

qij,i=htcij,iA‴ij(Tsat-Ti)

(6)

式中：τij,i为i与j相的相间摩擦作用在i相上的力；Cij为相间阻力系数，计算方法见表1，表中后缀GL代表气相与连续液相相间作用，GD代表气相与液滴相相间作用；ρi为各相密度；A‴ij为相界面面积；ui为当前相速度；uj为相对相的速度；qij,i为i相从相界面获得的能量；Tsat为饱和温度；Ti为相温度；htcij,i为i相相间换热系数，相间换热系数包括过冷液、过热液、过冷气与过热气4种状态，由于过热液与过冷气在物理上并不稳定，会迅速达到饱和态，因此程序中对过热液与过冷气设置了很大的换热系数，过冷液与过热气换热系数计算方法见表1。

2) 阻力模型

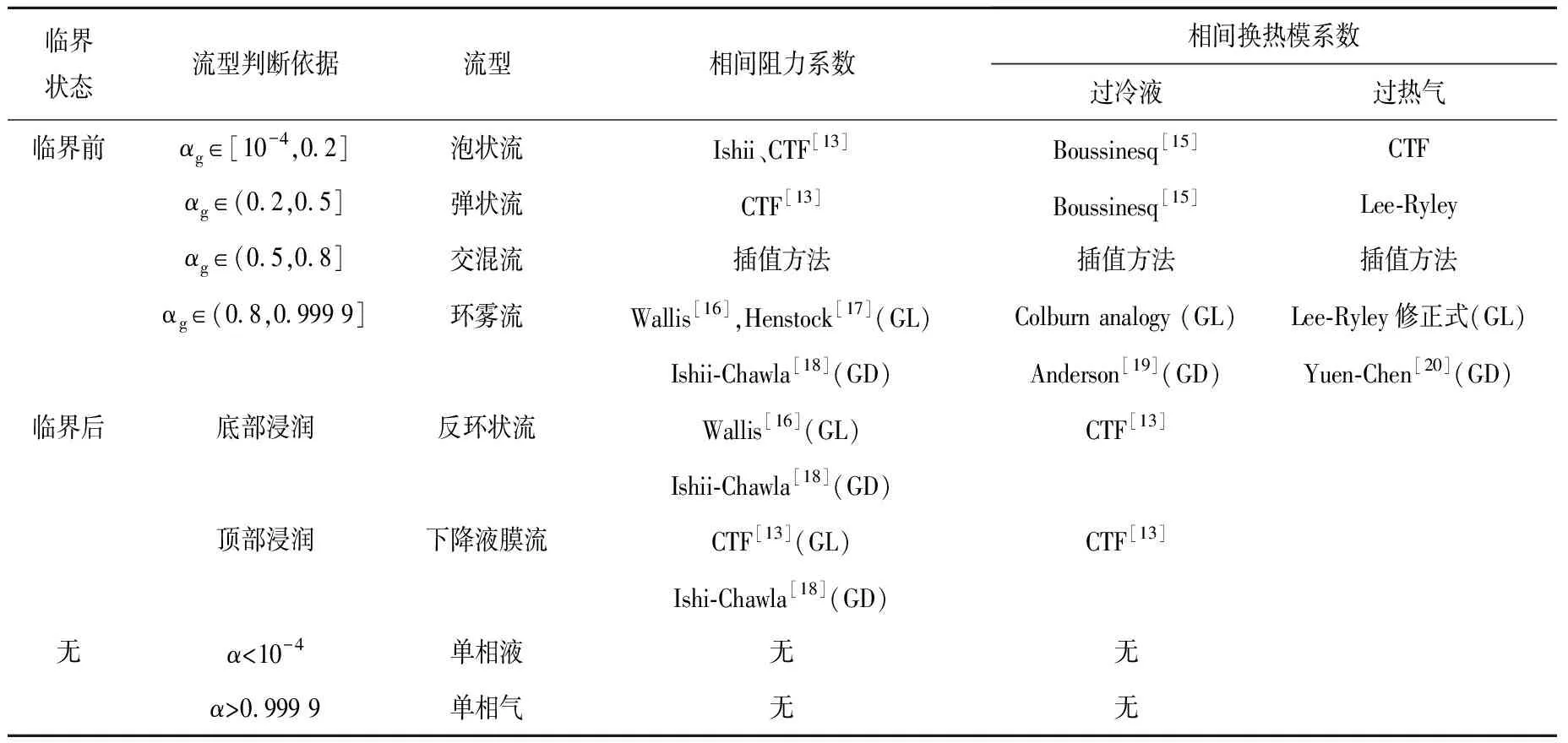
表1 流型图及相间作用模型Table 1 Flow regime and interphase model

(7)

式中：Cw为壁面摩擦系数，采用McAdam关系式[14]；Cf为形阻系数，由用户输入；G为流体的质量流率；φ为两相接触因子；Dh为通道的水力学直径；Δx为控制体长度；液滴相弥散于气相中且不于壁面直接接触，不考虑液滴相的阻力。

3) 交混模型

湍流交混是由于流体脉动时自然涡团扩散引起的非定向交混，交混模型是子通道程序特有的模型，其基于扩散效应，表征了相邻通道间的质量、动量以及能量的扩散现象。

质量、动量及能量交混关系式分别为：

(8)

(9)

(10)

式中：下标ab、a和ab、b分别代表相邻通道a、b作用于通道a和b的量；h为各相焓；u′为脉动速度；Agap为间隙面积；Vc为控制体体积。

脉动速度u′可表示为：

(11)

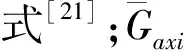
4) 液滴模型

在传统的中学地理教学活动中，我们老师可能或多或少的忽视了中学生地理学习中的知识情感、想象以及知识点的领悟等多方面的发展，。在地理课堂教学活动中老师过多地强调知识的记忆、模仿，抑制了学生的头脑意识，表达动手能力，导致学生地理思维能力欠缺、地理课堂活力不足，从根本上制约了学生的主动性和创造性,从而让我的地理课堂教学变得固执、沉闷，缺少了灵性，缺乏了活力。在新课改的要求下，教师必须改变教学方法使地理课堂教学活力从根本上得到提升。

液滴存在于临界后流型及临界前的交混流、环雾流中，这些流型的计算中需要考虑液滴模型。液滴模型包括夹带沉积模型及液滴相界面面积模型。其中，夹带与沉积模型表征连续液相与液滴相间的质量传递；液滴面积输运方程用于液滴相界面面积的计算，用于相间本构关系式。

夹带与沉积模型为：

Γd,ld=-Γl,ld=Γentr-Γdepo

(12)

式中：Γd,ld为液滴生成率；Γl,ld为液滴向连续液相中的净传质；Γentr为液滴夹带率；Γdepo为液滴沉积率。程序中液滴夹带沉积模型采用参考程序[13]的方法，夹带包括在环雾状流夹带、反环状流夹带、下降液膜流夹带，沉积主要包括环雾状流沉积、横向流沉积以及面积变化带来的沉积。

程序中采用的液滴面积模型包括液滴相界面输运方程与临界韦伯数模型两种方法。液滴相界面输运模型为：

(13)

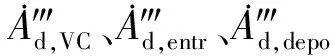
根据韦伯数(We)的定义，可得Wecrit与液滴直径Dd的关系：

(14)

程序中假定液滴为圆球形，因此，液滴相界面面积浓度A‴gd与Dd的关系为：

A‴gd=6αd/Dd

(15)

式(14)、(15)为临界韦伯数液滴面积模型，式中：σ为表面张力；ugd为气相与液滴相对速度；ρd为液滴密度；αd为液滴份额。

5) 壁面换热模型

壁面换热模型表征壁面与流体间的传热关系。壁面换热模型依赖于不同的壁面换热模式，程序中包括8种壁面换热模式，换热模式及对应的传热系数模型列于表2。壁面换热会导致流体发生相变，程序中仅考虑壁面换热所导致的液体蒸发效应，而不考虑壁面过冷导致的蒸汽冷凝现象。壁面换热关系式为：

qw,i=htcw,i(Tw-Ti)

(16)

(17)

式中：htcw,i为壁面向各相的传热系数，计算方法列于表2；Tw为壁面温度；qw,i为壁面向流体的传热量；式(17)为壁面换热导致质量传递，htcw,fg为壁面相变换热系数；hfg为汽化潜热；Msliq为网格中的液相总质量。为防止壁面换热导致液相蒸发过大，设定为单个时间步内的网格蒸发量不超过该网格连续液相总质量的80%。

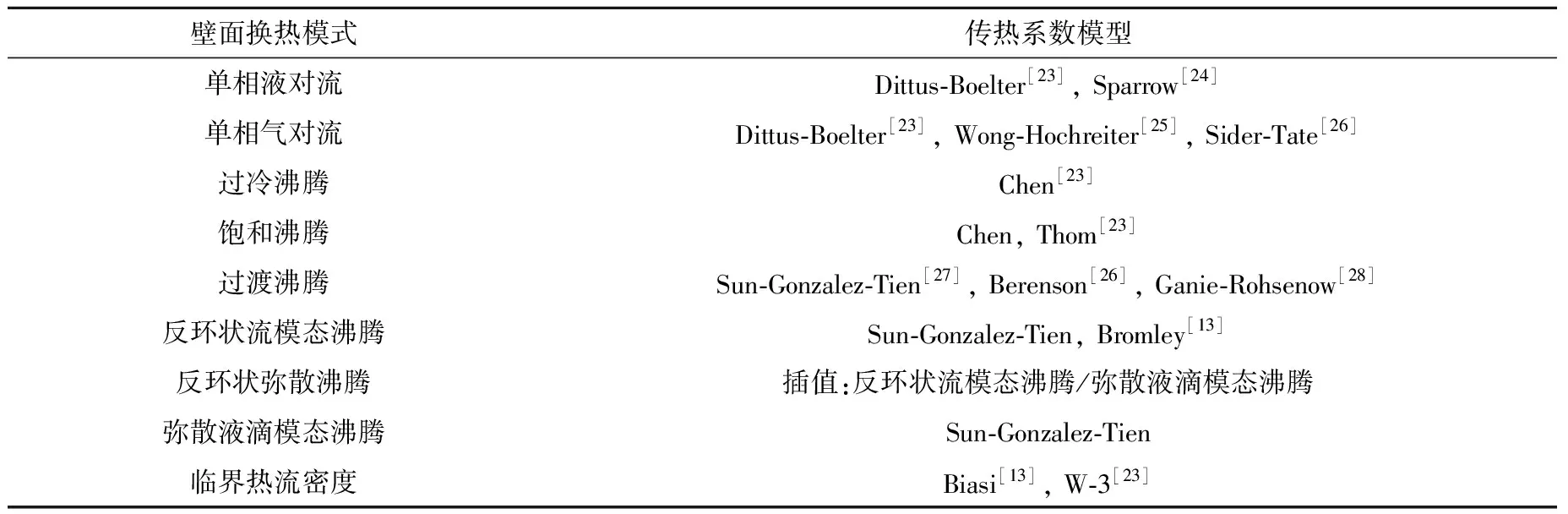
表2 流型图及传热系数模型Table 2 Flow regime and wall heat transfer coefficient model

6) 多相场子通道程序的计算流程

程序采用半隐式计算方法及Newton-Raphson求解器，并通过牛顿下山法提高计算收敛性，采用残差限值和库朗数限值判断计算是否收敛，求解流程如图1所示。

在每个时间步内，程序首先进行预处理并计算出求解器所需的各项，而后使用Newton-Raphson求解器求解新时刻的各主变量，其中，多相场子通道程序主变量包括11个主变量，分别为体积分数(αg、αd)，轴向与横向速度(ug、ul、ud、wg、wl、wd)，焓(hv、hf)和压力(p)；随后使用牛顿下山法判断是否需要松弛迭代，最后使用收敛准则判断程序是否计算收敛，并调整时间步长，进入下一次计算。

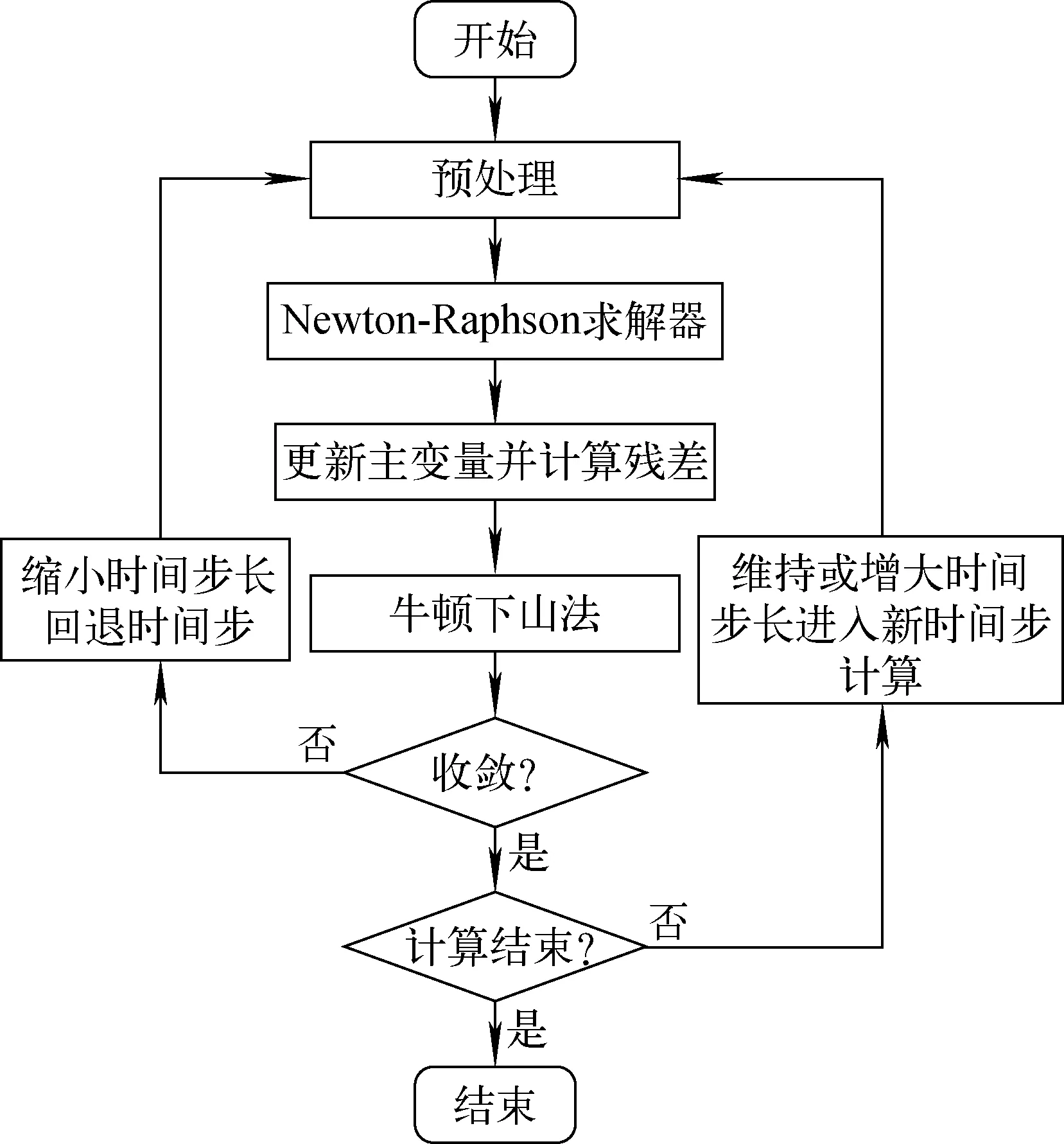
图1 程序计算流程 Fig.1 Calculation process of code

2 多相场子通道程序的评估

选取典型测试算例及实验工况对程序进行评估，验证程序计算的合理性与正确性。

2.1 液滴模型测试

采用参考程序COBRA进行对照，评估多相场子通道程序对液滴行为的计算能力，并进一步分析液滴尺寸对流场分布的影响。

1) 液滴模型评估

选取长度为1 m，直径为2 cm的单根圆管算例进行测试。如图2所示，通道划分为20个控制体，底部入口为气相份额为0.925的流动边界，入口处气相与连续液相速度分别为5.18 m/s及4.1 m/s，各相焓均采用饱和值，顶部出口为压力边界，压力为10 MPa。观察计算稳定后通道中流场分布情况。

液滴相弥散于气相中且具有较大的相界面面积，因此液滴相与气相间存在着较强的相间作用，图3展示了液滴测试中本程序与参考程序沿轴向通道的流场分布对照，本程序与参考程序的计算趋势符合良好。其中图3a展示了液滴模型开闭情况下气相速度的分布情况，开启液滴模型后，液滴份额沿通道逐渐增加，液滴相重力较大，因此速度较慢，在相间拖曳力的作用下，气相损失动能，气相速度会逐渐下降，而液滴相速度逐渐增加；关闭液滴模型后，气相仅存在与连续液相的相间拖曳力，该相间拖曳力较小，因此气相速度沿通道逐渐增加并最终达到稳定。图4为本程序与参考程序在流场参数计算中的误差分布，可以发现，气相份额、气相速度及液滴速度的计算相对误差小于5%，液滴份额相对误差小于10%，程序总体计算误差较小。因此，多相场子通道程序可以合理计算液滴相运动行为。

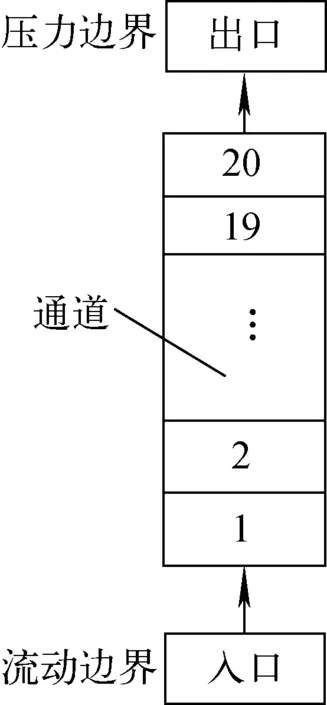
图2 液滴测试建模Fig.2 Model of droplet behavior test

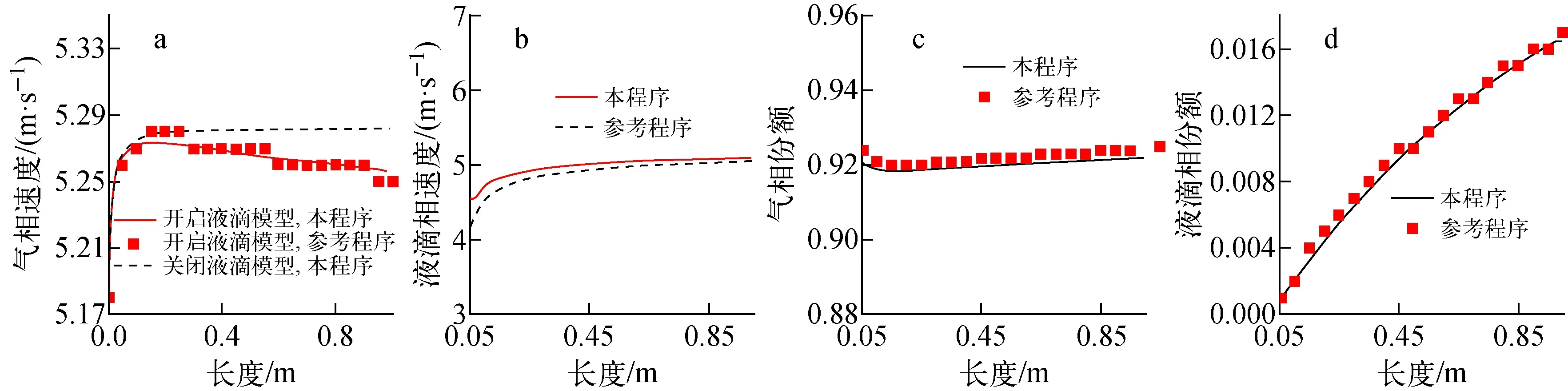
图3 液滴测试计算结果比较Fig.3 Comparison of calculation in droplet test

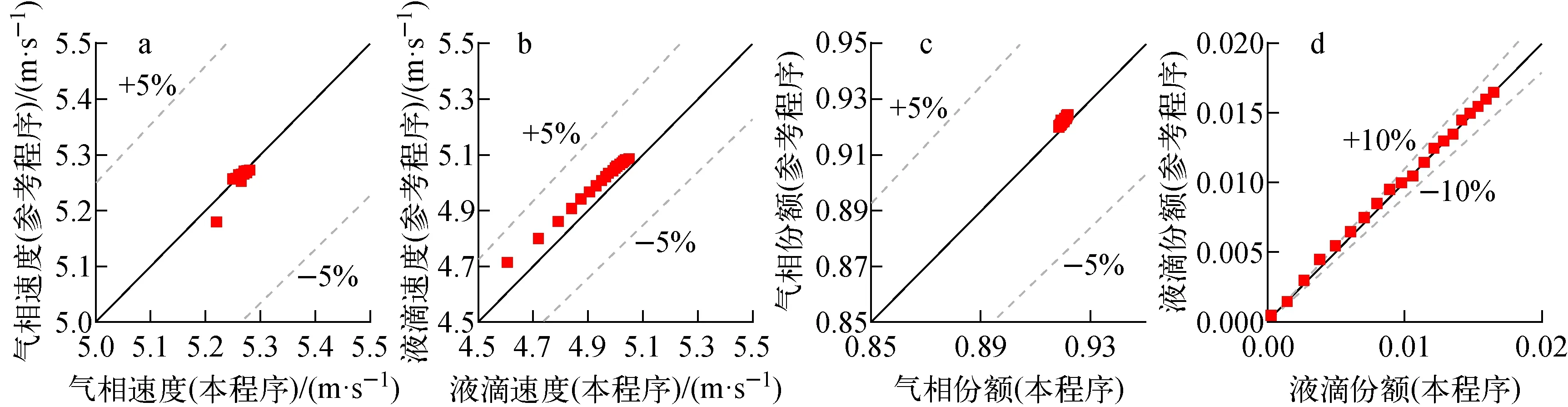
图4 计算误差分布Fig.4 Distribution of error in droplet test

2) 液滴尺寸对流场影响

多相场子通道程序中假定液滴为圆球形，液滴尺寸与液滴相界面面积呈反比。本测试通道长度为4 m，划分为40个节点，边界条件与算例1相同。本节采用临界韦伯数(Wecrit)方法控制液体的尺寸，设定Wecrit分别为2.0、3.0、6.0、12.0，测试不同尺寸的液滴对流场分布的影响(图5)。

由图5a、b可知，Wecrit越小，则液滴直径越小，液滴相界面面积越大，从而液滴的相间作用越强烈。由图5c、d可知，Wecrit越小，相间面积越大，气相与液滴相的相间拖曳力越强，因此计算稳定后的气相/液滴相的相对速度越小，对比不同Wecrit下的通道出口的液滴直径与气相/液滴相相对速度，可以发现，两者基本呈线性分布，即液滴直径越大，则流场中的气相/液滴相相对速度越大。

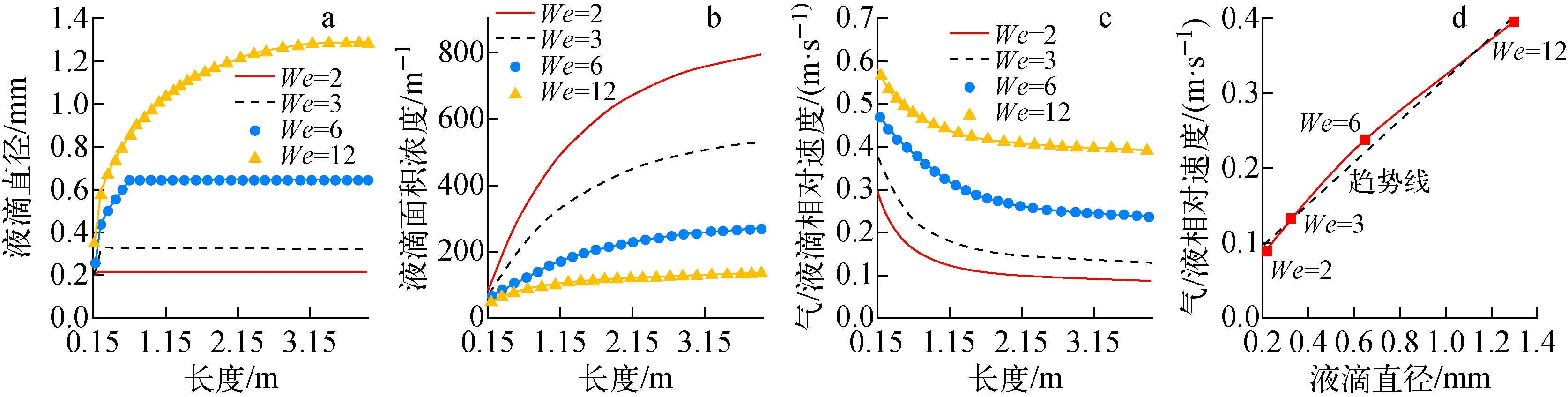
图5 不同液滴直径计算结果Fig.5 Calculation of droplet test with different diameters

2.2 湍流交混测试

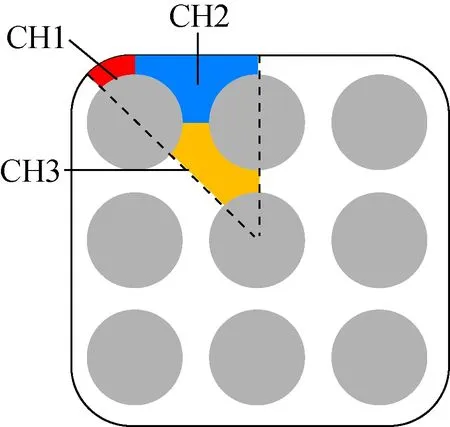
图6 GE3×3实验建模Fig.6 Model of GE3×3 experiment

选取GE3×3-1C棒束实验[29]进行湍流交混测试，实验中棒束长度为1.828 8 m，单根棒直径为0.014 5 m，棒中心距为0.014 7 m，棒束出口压力为6.895 MPa，通道中流入过冷水，过冷度为264 K，各通道中的入口质量流率均为1 342.67 kg/(m2·s)。3×3通道具有几何对称性，因此在程序中对棒束进行1/8建模。如图6所示，模型中包括3个通道，每个通道中设置有72个控制体，其中CH1为角通道，CH2为边通道，CH3为中心通道，各通道入口处的质量流率为1 342.67 kg/(m2·s)，观察计算稳定后各通道中质量流率沿通道的分布情况。

CH1为角通道，水力学直径最小，相同质量流率下壁面阻力较大，因而通道压降最大；CH3为中心通道，水力学直径最大，相同质量流率下壁面阻力最小，通道压降最小。在通道间压差作用下，CH1中流体通过间隙向外流出导致通道质量流量降低，而CH3中有来自间隙的流体流入导致通道质量流量增加。湍流交混体现了通道间的扩散效应，用于降低不同通道中的质量流率差异。图7为湍流交混测试计算结果。由图7可知，与关闭模型的结果相比，开启模型后CH1～CH3通道间的质量流率差值明显减小，CH1出口质量流率升高，而CH3出口质量流率降低，计算结果与理论分析相符。此外，计算结果与实验值符合良好，CH1～CH3通道出口流量的计算误差分别为0.62%、1.70%、0.098%，因此，多相场子通道程序可以准确计算通道间的湍流交混现象。

2.3 壁面传热测试

Bennet-Hewitt实验[30]是Bennet临界后实验，实验压力为6.89 MPa，入口处流入过冷度为12 K过冷水，入口质量流量为393 kg/(m2·s)，流体沿通道向上流动并被加热，壁面热流密度为0.393 MW/m2。流体沿通道流动被加热蒸发，壁面传热模式由临界前进入临界后，壁面温度在临界热流密度处发生突跳。装置建模如图8所示，通道划分为40个节点，入口和出口处分别为流动边界与压力边界。观察计算稳定后，壁面温度沿通道的分布情况。

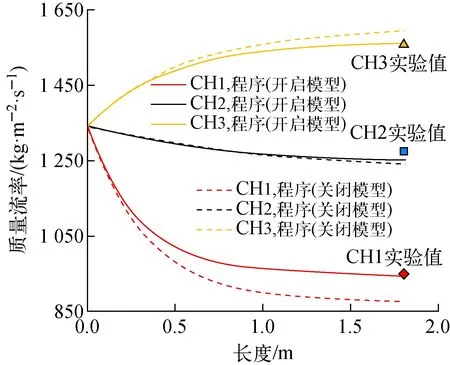
图7 湍流交混测试计算结果Fig.7 Result of turbulent mixing test

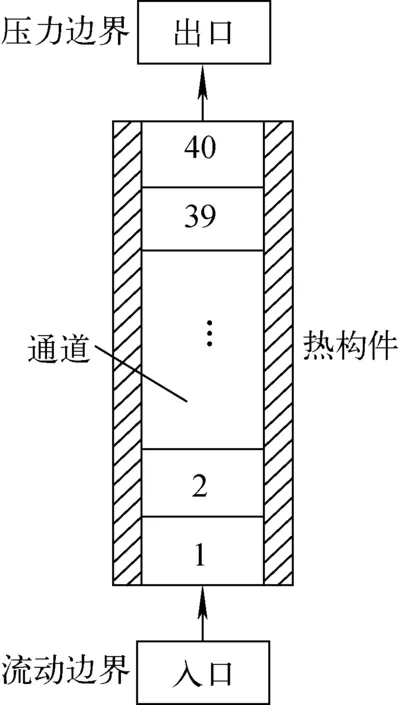
图8 Bennet-Hewitt实验建模Fig.8 Model of Bennet-Hewitt experiment

计算结果表明，由入口到出口，壁面传热模式由临界前过冷沸腾、饱和沸腾发展至临界后弥散液滴模态沸腾、单相气换热。壁面温度分布如图9所示，在临界前后传热模式转换点，壁面热流密度达到了临界热流密度(CHF)，壁面温度发生突跳，实验得到温度起跳位置在0.426处，计算所得起跳位置在0.45处，程序计算出的温度起跳位置较实验中延后。温度起跳点左侧的临界前传热模式，程序计算得到的壁面温度较实验值偏高，临界前壁面温度的计算误差小于+15%，说明程序采用的临界前壁面换热模型在计算中低估了壁面换热能力；临界后的计算温度与实验数值符合良好，实验值与计算值误差在±5%以内，说明由于具有液滴相换热并采用了合理的临界后壁面换热模型，程序可以很好地模拟临界后壁面换热工况。综上，程序可以很好地模拟跨临界的壁面换热工况。

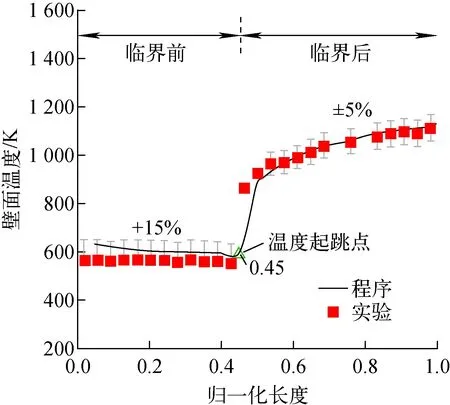
图9 壁面传热测试计算结果Fig.9 Result of wall heat transfer test

2.4 再淹没实验验证

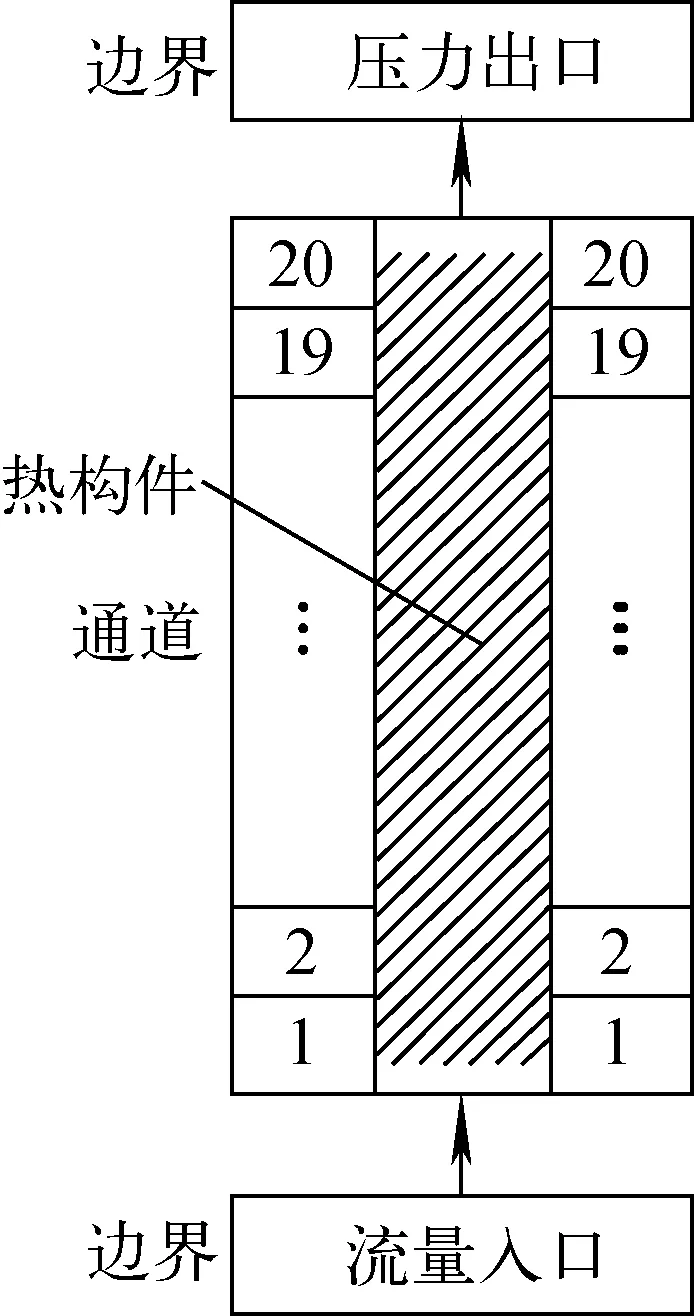
图10 FLECHT-TSP实验建模Fig.10 Model of FLECHT-TSP

FLECHT-TSP实验[31]为临界后低淹没速率实验，实验段长度为3.66 m，实验工况压力为275.79 kPa，加热棒峰值功率为2.3 kW/m，其中加热棒轴向功率分布沿顶部倾斜，最大峰均功率比为1.35。为验证程序预测顶部倾斜功率分布的再淹没工况的能力，对实验装置进行建模，如图10所示，包括20个轴向节点，流道内设置有加热棒，实验中过冷水以0.02 m/s的速度由入口沿着流道向上流动，计算时间为500 s，观测各监测点的壁面温度变化及骤冷时间。其中，实验段nd1～nd5观测点距离加热棒底端距离分别为1.016、1.676 4、2.286、2.895 6、3.200 4 m。图11为FLECHT-TSP计算结果。图12为计算误差分布。

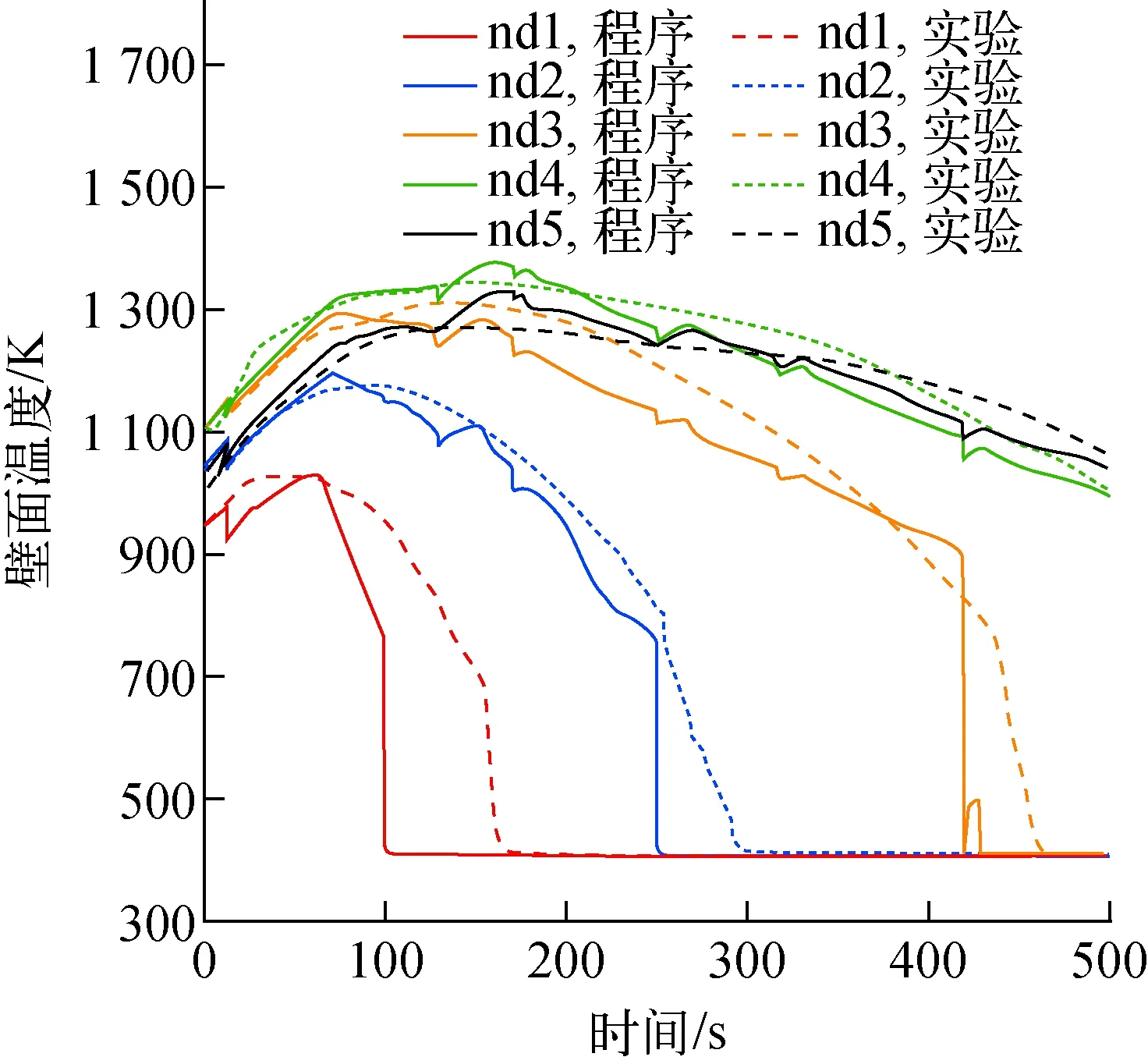
图11 FLECHT-TSP计算结果Fig.11 Result of FLECHT-TSP

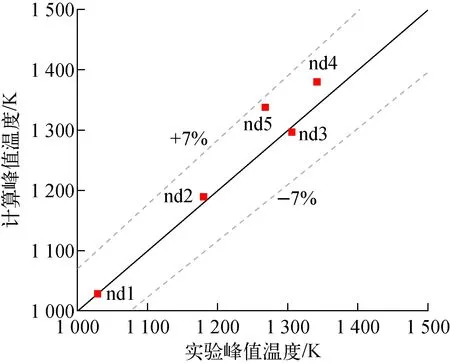
图12 计算误差分布Fig.12 Distribution of error

由图11可知，在计算开始后，由于加热棒功率较高且通道中仅含换热能力较差的单相气，加热棒表面温度迅速升高并进入临界后状态，随后底部灌水浸润了加热棒表面，加热棒由下至上，表面温度依次急剧下降并进入临界前状态，程序能较好地模拟出各观测点的壁面温度变化情况；但程序计算出的壁面温度下降速度较实验更快，这是由于程序中采用的壁面换热模型在临界前后的换热能力差异过大，当加热棒表面被浸润时，壁面传热模式由临界后进入临界前，换热系数迅速增大，流体从壁面处带走了大量热量，导致壁面温度迅速下降。由图12可知，计算得到的各监测点峰值温度较实验值稍高，各监测点峰值温度相对误差均小于7%，表明程序计算出的峰值温度是准确的，且结果具有一定的保守度。综上，程序计算结果与实验值整体符合良好，程序能较好地模拟堆芯再淹没工况。

3 结论

COSINE系列软件包经过多年的发展，已具备了压水堆核电站的热工水力分析等各种功能。为满足先进反应堆“国和一号”的工程设计与安全分析要求，需开发具有更高计算精度的多相场子通道分析程序。本文介绍了多相场子通道程序的物理模型和数值方法，并通过程序对照方法评估了液滴模型计算的合理性；随后，通过GE交混实验，评估了程序对子通道交混现象的计算能力；最后通过Bennet传热实验及FLECHT实验，验证程序在计算临界前后传热问题及再淹没问题上的模拟能力。结果表明，程序在含液滴工况的计算是合理的，程序对交混实验的计算结果与实验数据符合良好；在临界前后壁面换热及再淹没问题的计算中，程序可很好地模拟壁面温度的分布及再淹没工况下热工水力学参数的变化。因此，多相场子通道程序对堆芯热工水力学现象的计算是合理且正确的，程序已具备了对堆芯子通道热工水力现象的计算模拟能力。