气井多液滴携液理论模型研究

郭江波 许云凤

(1.陕西省天然气股份有限公司，陕西 西安 710016;2.陕西省液化天然气投资发展有限公司，陕西 西安 710065)

1 绪论

在已开发的气田中，气井存在不同程度的积液。气井积液的危害很大，不但减少产量，严重时会堵死气井，而且还会增加排水采气的作业成本。石油工程师对气井携液理论进行了大量的研究。1961年，Duggan 经过对现场大量的数据整理，提出了最小气体流速的概念。Turner 在1969年提出了液滴模型，Turner 假设液滴在高速气流携带下是球形液滴，通过对单个球形液滴的受力分析，得到了气井携液的临界流速公式。此后，Coleman 在研究了大量低压气井的生产数据后，推导出了新的低压气井的临界流速公式。2000年Nosseir年建立瞬变流模型和紊变流模型。2001年，李闽以液滴在多个力作用下会变成一椭球体的思想，得到了新的临界流速模型。尽管如此，这些研究都是单个液滴分析思想，其实上，气体在管流中，可能会发生多液滴碰撞、分离、回落、聚合、碰碎等情况。Zhou and Ruan 提出了多液滴理论雏形，并给出了气井的经验临界流速公式，与Turner 及Turner 校正公式进行对比。

本文将多液滴理论引入气井气体携液理论研究中，通过分析液滴在气流中的受力和运动情况，建立完整的气体多液滴携液理论模型，即考虑液滴在气流场中的运动、碰撞、聚合和破碎等种种情况进行研究，探索出更适用的计算模型。

2 新理论模型的建立

2.1 单个液滴受力分析

图1 液滴受力分析图

按照李闽等人的研究成果，液滴在井筒中会是个椭球形，气井中液滴主要受三种力的作用，即液滴自身的重力G，气体对液滴的悬浮力F1和气体在流动过程中对液滴的曳力F2。同时，液滴在管流中，由于气体紊流，应该具有一个初速度V，这也是本文不同于经典的Turner 模型的所在。如图1 所示。

2.2 单个液滴运动轨迹分析

以液滴为研究对象，建立坐标轴，如图2 所示，推导理想速度方程，得出其迹线。

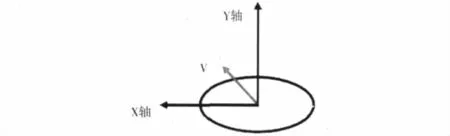
图2 液滴二元运动速度坐标轴

把初始速度V 分解为X 轴和Y 轴的速度为Vx 和Vy，则井筒中任意处X 和Y 方向的速度可以写为:

式中，a 为液滴受到拽力、浮力和重力的合力作用的加速度;t 为运动时间。

假设速度V 为一常数，则液滴的运动轨迹方程为:

由公式(1)可知，其运动轨迹为抛物线。

假设气井深度H，井筒半径R，速度V 与X 轴夹角为α，液滴质量为M，如果液滴恰好被携带出井口且刚好不与井筒壁面碰撞，则由式(3)可得到液滴最小速度V 的表达式为:

对于携液临界速度，公式(4)中F1+F2=G，于是得到携液临界速度:

由Turner 及李闽对临界携液速度的推导过程，有:

式中，V 为液滴在气流中的运动速度，m/s;ρl为液体的密度，kg/m3;ρg为液体的密度，kg/m3;g 为重力加速度;σ 为气液表面张力，N/m;CD为曳力系数，无因次。

得到液滴不与管壁碰撞的临界携液速度方程为:

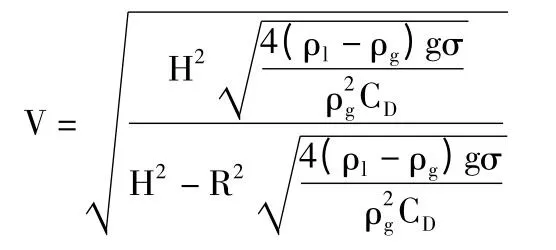
当液滴不与管壁碰撞时，临界携液速度方程必须满足:

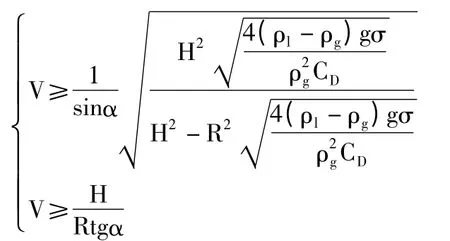
如果与管壁碰撞n 次，且为弹性碰撞，则临界携液速度方程为:

且当液滴在垂直方向的速度大于携液临界速度时，则液滴的轨迹如图3 所示。如果液滴速度小于携液临界速度，则会坠落至井底。

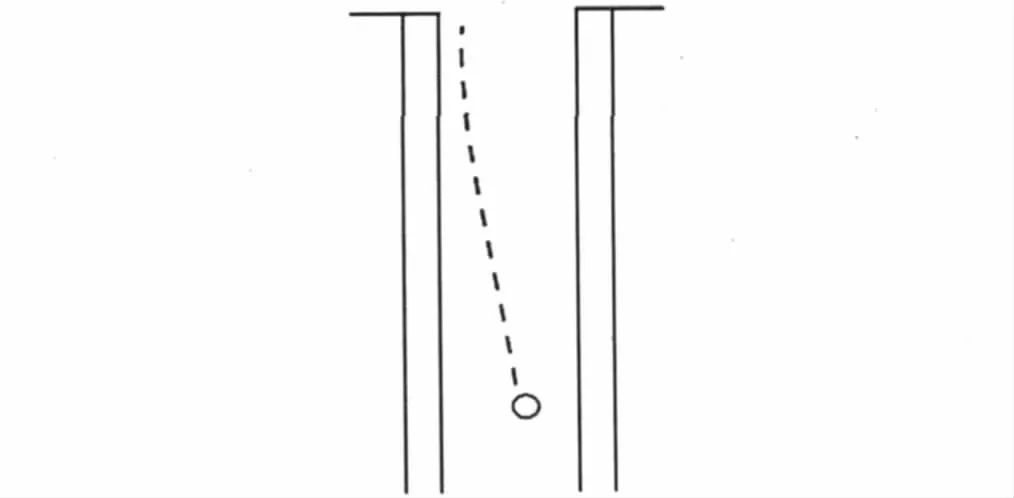
图3 气井中液滴的运动轨迹

若液滴在运动中与管壁发生弹性碰撞。当液滴垂直方向速度大于携液临界速度时，图4 所示的为一种可能的运动轨迹。否则，就会坠落至井底，变成积液。

图4 液滴在运动中与管壁相撞后可能的运动轨迹

2.3 液滴与筒壁碰撞理论

液滴与管壁碰撞结果与以下两个无量纲参数有关:

(1)液滴碰壁韦伯数We

式中，ρ 为液滴的密度，kg/m3;un为液滴撞击壁面的法向速度;d 为液滴直径，m;σ 为液滴的表面张力，N/m。

(2)液滴雷诺数Re

式中，μ 为粘度，Pa·s。

液滴碰壁后，有四种可能结果:黏附、反弹、沉积和飞溅。Escure【6】不考虑液滴碰壁后的黏附现象，引入参数K:

提出了液滴碰壁结果判断准则:①当K≤3 时，液滴碰壁后反弹;②当3 ＜K≤57.7 时，液滴碰壁后沉积;③当K ＞57.7时，液滴碰壁后飞溅。

图5 运动碰撞参数定义

2.4 液滴间碰撞理论

由于气井中气流的不稳定，液滴会发生相互碰撞。

现以直径为d1和d2的两个液滴为例进行分析，如图5 所示。对一般的二元液滴碰撞，往往与以下三个无量纲参数有关:

(1)碰撞韦伯数(We)，即液滴惯性与张力之比

式中，u1与u2分别为较大和较小液滴的速度矢量，m/s;d2为两液滴中较小的液滴的直径，m。

(2)无量纲参数B，其计算公式为

式中，b 为空间碰撞参数。

其中，b 为两个相互碰撞的液滴的连心线在相对速度矢量的法向的投影，它确定了碰撞液滴间空间方位的影响，定义为碰撞偏心距。当液滴发生碰撞时，B 值在0～1 之间变化。当B=0 时，液滴为对心碰撞;当B=1 时，液滴恰好相切而过。

(3)液滴半径比Δ，起计算公式为

两个液滴一旦发生碰撞，碰撞结果可以通过一定Δ 时的We－B 图显示。图6 为实验得出的Δ =1 时烃液滴在标准状态空气中碰撞结果。

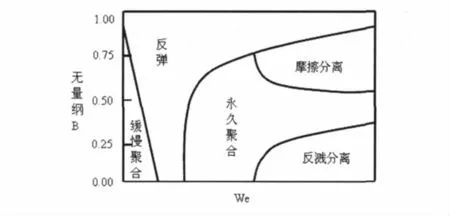
图6 液滴碰撞结果的分布示意图

由图6 可知，碰撞会出现以下几种可能性:即缓慢聚合、反弹、永久聚合、反溅分离和摩擦分离。而对于碰撞后的液滴速度，可以通过动量守恒和能量守恒计算得到。

1)聚合与摩擦分离

Brazier－Smith 根据试验给出了发生摩擦分离的判定准则为

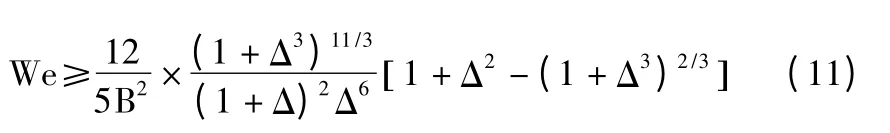
可见，液滴碰撞聚合形成较大液滴可能以较慢速度继续上升或在自身重力作用下坠落，这取决于临界速度的大小。

2)聚合与反溅分离

Ashgriz 和Poo［11］建立了聚合－反射分离间的边界模型，经计算与试验结果的对比，确定发生反射分离的准则为

液滴相撞后发生反溅，向四周释放出小液滴。这些较小液滴将以更快速度被气体携带出井口。

3)聚合与反弹

Estrade 等基于试验观察，推导了关于液滴碰撞反弹的判定准则，忽略液滴变形过程中的黏性耗散作用，得到

τ=(1－B)(1 +Δ)

式中，φ 为液滴形状因子，表征液滴的变形量;θ 是液滴碰撞时连心线与液滴相对速度的夹角。

2.5 液滴的碰撞概率

O‘Rourke 模型用随机的方法计算液滴的碰撞概率，当两个液滴以相对速度u 运动时，如果两个液滴的运动轨迹在半径为的范围内，两液滴就有可能发生碰撞，计算时将大液滴看作是集合液滴，若液滴分布是均匀分布，根据气体分子的运动理论，小液滴碰撞的概率P 为

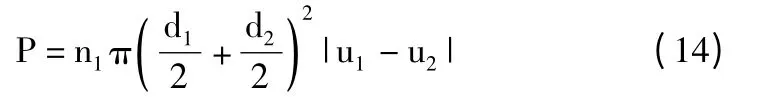
式中:n1为小液滴在单位体积内的液滴数密度。

3 液滴破碎模型

液滴聚合成较大液滴后就有可能再发生破碎。液滴在气流场中主要受气流作用下的压力和剪切力和液滴表面表面张力作用。气井流场对液滴的作用力使液滴变形、破碎，而表面张力阻碍变形使其保持球状。将液滴所受气动力与其表面张力之比定义为液滴的气动韦伯数，即

式中，ρg为气相密度，kg/m3;ul为气相速度，m/s，dl为液滴直径，m。

气动韦伯数是一个无量纲参数，Weg越大，液滴越不稳定，越易于变形破碎。Pilch 和Erdman 对高速空气流中水滴的破碎实验研究发现，随Weg变化液滴破碎分为4 种形式:

(1)振动破碎。Weg≤12 时，气体流速较低，液滴表面在气动力作用下发生变形并出现振动，液滴与流场的共振使得变形不断扩大，并最终破碎成几个子液滴。振动破碎的子液滴较少，粒径较大。

(2)袋状破碎。12 ＜Weg≤80 时，液滴在气动力作用下形成袋状结构并最终破碎，破碎首先从最薄的袋状中心部位开始。

(3)剥离破碎。80 ＜Weg≤350 时，相对速度较大，被拉成扁平的液滴，在高速气流强大曳力的作用下，加上液滴表面的剧烈震荡，从边缘开始剥落分离。

(4)毁灭破碎。Weg＞350 时，液滴表面形成高频率、大振幅的震荡，在高速气流作用下，液滴迅速破碎成细小液滴。

4 结论

通过对气井井筒中液滴运动情况、液滴与管壁碰撞、液滴间碰撞及液滴破碎的研究，得到如下结论:

以气井中液滴的受力分析和液滴间碰撞为主要研究对象，建立了新的气井气体携液模型。

给出了液滴与管壁碰撞、多液滴间碰撞、液滴破碎等模型及相关判断公式。

从理论分析来看，气井携液应该考虑到液滴碰撞、破碎等情况，将会更符合气井管流实际。

［1］Turner，R.G.Analysis and Prediction of Minimum Flow Rate for the Continuous Removal of Liquids from Gas well［J］.J.Pet.tech，Nov 1969.

［2］Coleman，S.B.A New Look at Predicting Gas Well Load Up［J］.J.Pet.Tech，Mar 1991.

［3］Nosseir，M.A.A New Approach for Accurate Prediction of Loading in Gas Well Under Different Flowing Conditions［J］.spe37408.

［4］李闽，郭平，谭光天.气体携液新观点［J］.石油勘探与开发，2001，28(5):105－106.

［5］Desheng Zhou and Hong Yuan.A new model for predicting gas－well liquid loading.SPE 120580－PA:172－181.