离心萃取级联分离锂同位素的数学模型
2022-09-06李维杰葛超奇张孟琦武中地
张 睿,闫 昊,李维杰,葛超奇,张孟琦,王 欢,车 军,武中地
(中核第七研究设计院有限公司,山西 太原 030012)
在自然界中主要存在两种锂的同位素,6Li和7Li,6Li的相对丰度为7.45%,7Li的相对丰度是92.55%。7Li的特点是对于中子的反应截面很小,在核裂变反应的调控以及对于设备的维护上有着重要的作用;6Li是核聚变的原料,热中子轰击6Li可产生氚,6LiD是国防科技领域非常重要的一种核材料。
锂同位素的分离在国内外一直是一重要课题,到目前为止,投入工业生产的主要方法是锂汞齐法。锂汞齐法的特点是分离系数高、同位素交换速度极快、效率高,但生产过程中需使用大量的汞,对于环境会产生极大危害。其他分离锂同位素的方法包括离子色层交换法[1-3]、熔盐电解法[4]、分级结晶和沉淀法[5]、分子蒸馏法[6]、激光法和萃取法,但均未投入工业化生产。上述方法中,萃取法去除了汞造成的污染,有较高的分离系数,与高效萃取装置离心萃取机结合构建成级联,对锂同位素分离有很大的潜力。本文对离心萃取级联分离锂同位素的过程进行研究,并建立数学模型。
1 分离原理和分离系数
溶剂萃取体系分离锂同位素主要利用了6Li和7Li在两相溶剂中的分配系数的差异分离锂同位素,用作萃取剂的体系主要为醇酮体系[7-9]、烷基膦和膦酸酯体系[10-12]和冠(穴)醚类体系[12-20],冠(穴)醚类萃取体系是目前已报道萃取分离锂同位素种类最多且分离效果最好的体系。
实现锂同位素分离的关键在于合适的萃取体系,该体系至少应满足以下3个条件:1) 互不相溶的两相即通常为有机相和水相组成的稳定萃取体系,该体系中对锂有合适的分配系数;2) 锂在两相中处于不同状态,存在一定差别,存在同位素效应;3) 两相接触同位素交换速度足够快。合适的萃取体系满足上述条件的1和2,离心萃取机可增加两相流的接触,加快同位素交换速度,满足条件3。
在萃取法中,核心阶段是同位素交换段,锂同位素的交换过程(以富集6Li为例)如下式所示:

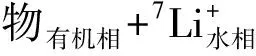
用浓度c表示交换反应的平衡常数,有:
(1)
其中:Kθ为反应平衡常数;k为萃取体系各同位素的分配系数;α为全分离系数。
2 建立模型
在离心萃取分离过程中,为使同位素交换段分离过程更简单可靠,选择合适的平衡条件(通过调节相比、温度、酸碱度等方式实现),使该条件下交换段不发生萃取和反萃,仅进行同位素交换反应,在此基础上建立分离模型。
2.1 单级分离模型
体系中有机相S质量为MS,水相B质量为MB,溶质(包含6Li和7Li)质量为MA,有机相和水相完全不互溶,且在恒定条件下以质量比组成的分配系数为常数K(萃取平衡状态),有机相中溶质质量M1,水相中溶质质量M2。可通过物料守恒和平衡状态的分配系数K求得有机相和水相中的含锂量:
(2)
根据质量守恒和同位素交换反应方程(分离方程),得到:
(3)
其中,C为丰度。类似气体离心级联,引入分流比θ,分流比为精料流量与供料流量之比,有机相水相相比为k,分流比为:
(4)
选取α为1.026的萃取6Li的萃取体系[13],在不同分流比下,取天然丰度的锂分离,单级分离后,不同分流比分离后精、贫料丰度如图1所示。
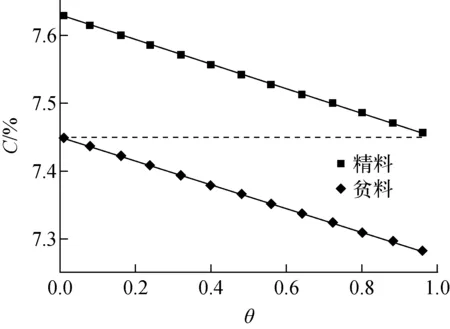
图1 单级萃取分离的丰度和分流比Fig.1 Abundance and split ratio in single-stage separation
随分流比的增加,精料丰度和贫料丰度逐渐减小。分流比越小,得到精料产品的丰度越大,但精料流量变小,目标组分更多地被分配到贫料中,导致原料利用率下降。若萃取体系中萃取剂和稀释剂部分互溶,在确定A、B、S组分后,可参照萃取体系的分配曲线确定两相中溶质的配比从而确定分流比。
2.2 多级分离模型
多级分离中,同样地,理论上最理想的同位素交换段不发生萃取和反萃过程,只发生同位素交换,流程如图2所示。
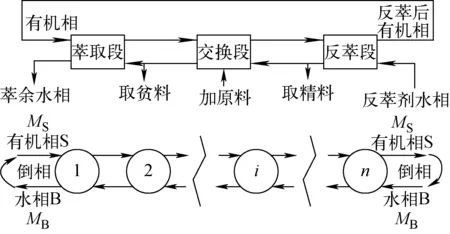
图2 多级萃取分离锂同位素流程简图Fig.2 Process of multi-stage extraction lithium isotope separation
在同位素交换段中,由于水相和有机相在各级中为连续流,理论上每级的有机相和水相之比以及锂在各相中的含量都完全相同。有机相在同位素交换完成后,经过反萃过程倒相转化成水相,重新逆流回同位素交换段,精料的取料在反萃后完成;水相在同位素交换完成后,即可得到贫料,经过萃取过程倒相转化成有机相,重新逆流回同位素交换段。多级分离的同位素交换过程近似于一个全回流矩形级联。每级有机相中锂含量(流量)为M1,每级水中相锂含量(流量)为M2,只发生同位素交换反应,全回流条件下,有:
M2CP+M1CW=M1CP+M2CW
(5)
即要满足M1=M2,各级分流比为0.5。
在不考虑取料情况下,级联平衡后各级丰度方程为:
(6)
贫料有类似表达式,由于α-1≪1,且丰度沿级联变化缓慢,因此,将式(6)改成微分方程,全级联丰度方程为:
(7)
无取料情况下,同位素交换段的最少理论级数为:
(8)
考虑有取料,取料会影响丰度分布,此时的实际分流比为:
(9)
其中,P为精料取料量,相较于精、贫料流量很小,因此分流比也近似为0.5。代入分流比的富集物质物料守恒方程:
(10)
联立式(6)和(10),写成微分形式,有:
(11)
同样的,对于贫化段,有:
(12)
分流比近似为0.5,浓化段和贫化段级数分别为:
(13)
(14)
2.3 平衡时间模型
级联分别有3段过程:同位素交换段、萃取回流段、反萃回流段,只有当3段均达平衡后,级联才处于稳定状态,仅在该状态下取料才能得到相应的产品,平衡时间的主要影响因素是同位素交换段的平衡时间。
非定常态的级联方程求解通常较复杂,一般通过试验求得物理图像估算。根据级联理论,一般平衡时间取决于浓化区,从初始状态到稳态,浓化区富集物质含量增加,可根据平均净富集物质的输运速率,估算平衡时间,如下式:
(15)
初始时以供料丰度CF为原料,则有:
(16)
其中:Hn为第n级容量;Cn为定常态时第n级丰度。设Gn为第n级流量,对于多级离心萃取采用的全回流矩形级联形式,每级容量和流量都为常量,分别为H和G,每级停留时间也为常数τ,则浓化区富集物质增加量为:

(17)
联立式(7),积分得到:
(18)
在趋于平衡过程中不取料,级联浓化区平均净富集物质输运速率为初始时间的输运速率的1/2,即:
(19)
则级联平衡时间为:
(20)
中国科学院上海有机化学研究所通过多级串级离心萃取装置(转子直径20 mm),采用SH-3型萃取剂(7Li分离体系,分离系数1.019)将7Li同位素从92.337%富集到99.043%,平衡时间约13 d。采用平衡时间模型,根据此条件计算级联平衡时间为级停留时间的14 827倍。根据调研,此规格离心萃取装置持液量约为0.5 L,混合通量最大约为25 L/h,则级停留时间最大约为72 s,通过模型计算得到的级联平衡时间最少为12.36 d,与试验结果基本吻合。
3 计算与分析
3.1 取料对级联的影响
取料量影响富集或贫化的级数,由式(13)、(14)可知,随着精料取料量(百分比形式)P/(M1+M2)和贫料取料量W/(M1+M2)增大,相同丰度下级数逐渐增加。但取料量存在极限,即当大于该取料量时,富集率dC/di≤0,不再发生富集/贫化,此时式(11)、(12)可写成:
(21)
(22)
体系的分离系数取1.026计算,式(21)、(22)不等号右边在丰度C为供料丰度时取最小值,在不同目标精料、贫料丰度下,理论最大取料量如图3、4所示。
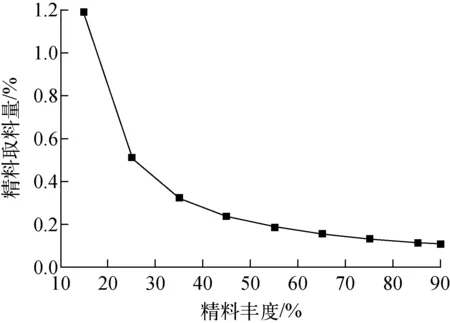
图3 不同目标精料丰度的最大取料量Fig.3 Maximum productive capacity in different target concentrate abundances
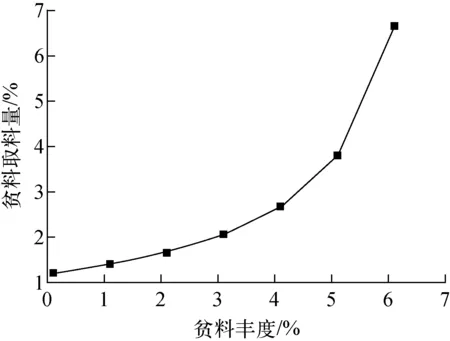
图4 不同目标贫料丰度的最大取料量Fig.4 Maximum productive capacity in different target waste abundances
随着目标精料丰度的增大,精料理论最大取料量减少;随着目标贫料丰度的减小,贫料理论最大取料量也减小。目标精料丰度为90%时,理论最大精料取料量为0.108 5%;目标贫料丰度为1%时,理论最大贫料取料量为1.389%。
不同目标丰度在不同取料量下富集(贫化段)的级数随精料、贫料取料量变化如图5、6所示。
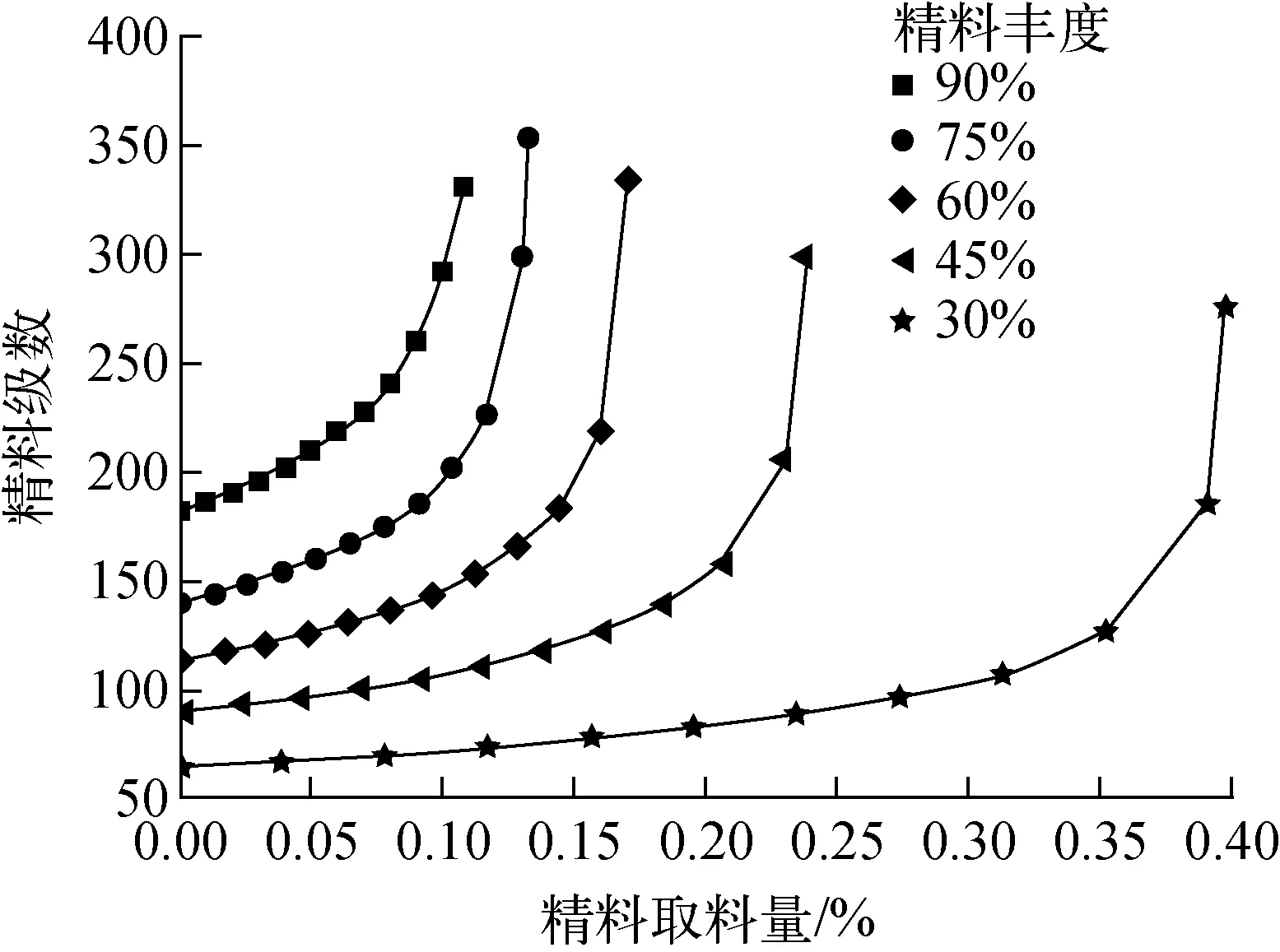
图5 不同目标精料丰度的富集段级数和取料量Fig.5 Number of stages of enrichment section and productive capacity in different target concentrate abundances
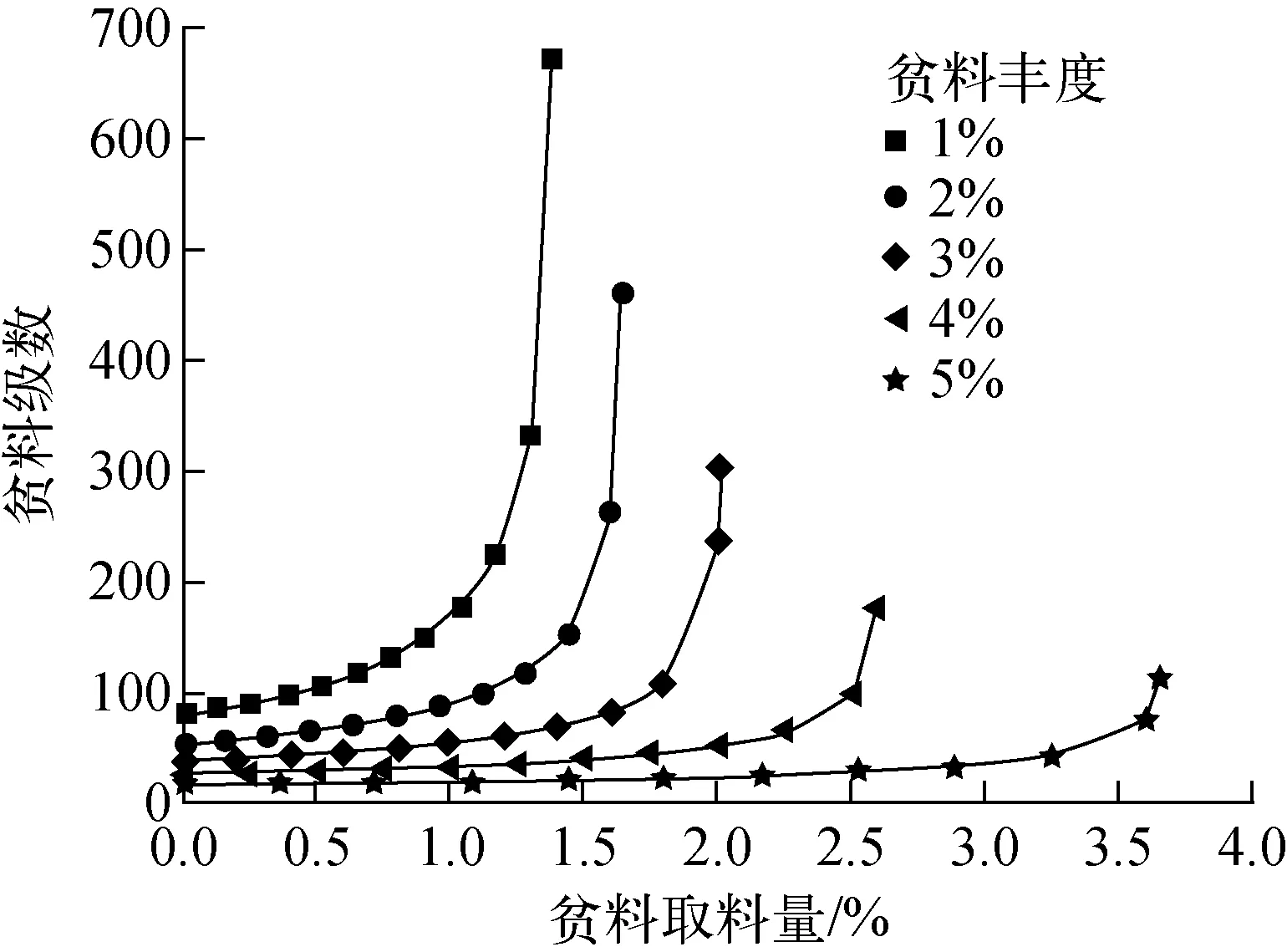
图6 不同目标贫料丰度的贫化段级数和取料量Fig.6 Number of stages of depletion section and productive capacity in different target waste abundances
目标精料丰度为90%时,所需最小理论级数(全回流)为182级,当选定最大取料量(0.108%)时,所需理论级数为330级;目标贫料丰度为1%时,所需最小理论级数(全回流)为80级,当选定最大取料量(1.38%)时,所需理论级数671级。因此在相同产量下,需综合考虑取料量和级数:增大取料量可减少总流量但会增加总级数,减小取料量可减少总级数,但总流量会相应增大。
3.2 级联的平衡时间
根据式(20)可估算级联的平衡时间,级联的平衡时间和萃取剂的分离系数、离心萃取装置的持液量及混合通量(用于计算级停留时间)、供料丰度和精料丰度相关。体系的分离系数取1.026计算,供料丰度为天然丰度,不同目标精料丰度的平衡时间(以级停留时间的倍数τ计)列于表1。
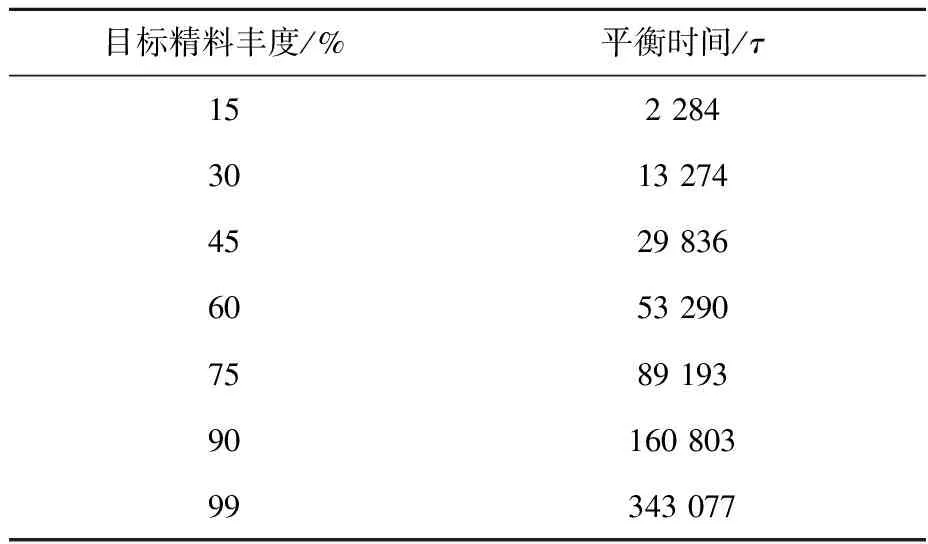
表1 不同目标精料丰度的级联平衡时间Table 1 Equilibrium time in different target concentrate abundances cascade
以目标丰度90%计算,通过某厂家不同型号离心萃取机持液量和混合通量的参数,其级停留时间在8~180 s之间,平衡时间为14~335 d。离心萃取装置处理量越大,级停留时间越短,平衡时间越短。
通过1个级联从天然丰度产品获得高丰度产品需要的平衡时间较长,可考虑采用多步法,即先将天然丰度原料富集到中间丰度,再从中间丰度富集到高丰度,这种方式平衡时间显著降低,一旦出现故障,恢复时间较短,级联有较好的稳定性。采用多步法的平衡时间(级停留时间倍数计)列于表2。
4 结论
本文建立了离心萃取分离锂同位素过程单级和级联的数学模型,利用程序对级联取料和级联平衡时间进行计算求解,得到如下结论。
1) 离心萃取级联是一种类似全回流矩形级联,级联取料量(回流量)对级联级数有重要的影响,级联的取料量存在最大值,随着取料量的增大,富集(贫化)段级数也会增大。
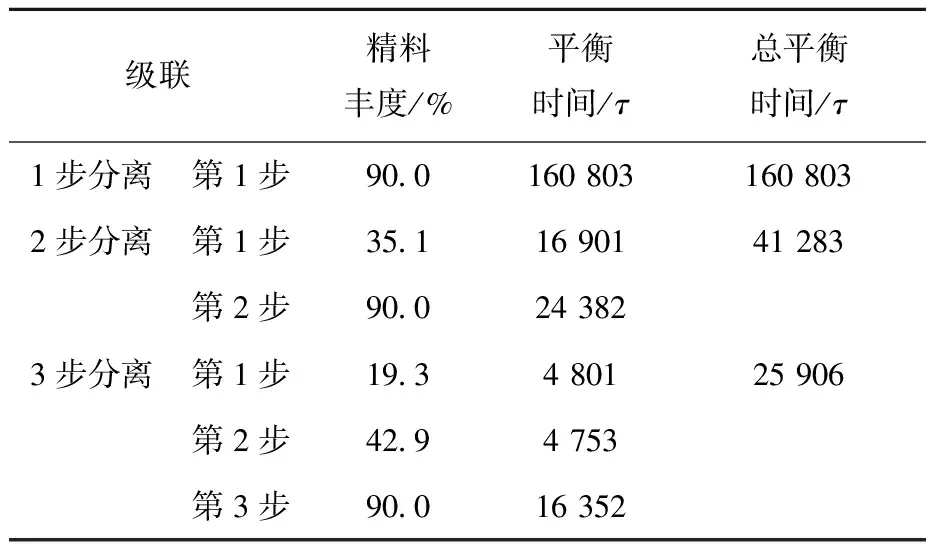
表2 多步级联的平衡时间Table 2 Equilibrium time in multi-step cascade
2) 级联的平衡时间与分离系数、离心萃取装置的级停留时间、供料丰度和精料丰度有关,分离至高丰度平衡时间较长,离心萃取装置处理量越大,平衡时间越短,可考虑采用多步级联富集高丰度产品,可显著降低平衡时间。
建立离心萃取级联分离锂同位素的数学模型为萃取法分离锂同位素及其工程化应用提供了一定的理论指导和依据。
