基于学徒制算法的航母舰载机保障作业调度

吴靳，戴明强，王俊杰，余珊珊，余明晖

1 海军工程大学 电子工程学院, 湖北 武汉 430033

2 海军工程大学 基础部, 湖北 武汉 430033

3 华中科技大学 人工智能与自动化学院, 湖北 武汉 430074

0 引 言

舰载机作为航空母舰（以下简称“航母”）上最重要的战力组成部分，其出动架次率是评价航母战斗力的重要指标之一。然而，因航母甲板的空间有限，航行环境具有不确定性，致使保障作业调度效率受到限制[1]。舰载机保障调度问题的优化目标是最小化一波次出动舰载机的最大保障完成时间。

以往，保障作业调度计划都是由调度工作人员根据军事演习或是实战经验制定的[2]。然而，随着计算机技术的发展，科研人员为了更加有效地求解保障调度问题，已尝试过采用多种智能搜索算法，例如遗传算法、禁忌搜索算法、贪婪算法及其衍生算法等。

针对航母上舰载机调度这一特殊场景，主要从如下2 个方面开展研究：一是如何对一波次出动舰载机进行保障战位分配；二是如何安排一波次出动舰载机的保障作业调度计划，从而令一波次出动舰载机的最大保障完成时间最短。针对舰载机保障战位分配的 问题，现有研究已涉及舰载机飞行甲板布列[3-4]以及陆基机位分配[5-6]等领域。针对保障作业调度问题，国内外学者也运用数学规划[7-8]、机器学习[9-11]、模拟仿真[12-13]等技术解决了一些难点。这些方法的使用在一定程度上缩短了舰载机的保障完成时间，提高了保障效率。但是，其基本流程大多是根据各项约束去建模，然后在可行解集合中搜索出问题的最优解，一旦问题的规模变大，全局搜索需要的时间就会成倍增长，且不一定能够找到最优解。

因此，为了解决大规模的舰载机保障调度问题，并优化求解速度，本文将在现有国内外舰载机保障作业相关研究的基础上，以一波次出动舰载机最大保障完成时间为优化目标，将机器学习应用于专家示例。然后，再将调度人员制定的保障调度方案作为专家示例进行学习，学习他们在做每一步决策时的思路，通过分析专家示例，构造基于成对比较模型的输入样本集，选取最优的分类算法来训练分类器，在此基础上构造学徒制调度算法。最后，使用学徒制算法和遗传算法分别针对新实例问题制定保障作业调度方案，以验证学徒制算法与传统算法效果。

1 舰载机保障调度模型建立

1.1 保障战位分配

新一代的航母大多选择采用“一站式”保障模式[14]。对于这类采用“一站式”保障的航母，其加油站的位置是固定的，能够使用该加油站进行加油的机位分布在一个以该加油站为顶点的扇形区域内，因此会出现多个加油站可加油的机位重叠现象，即一个机位可以使用2 个加油站中的任意一个完成加油任务。加油站的数量和位置约束以及其他保障资源约束，会使得舰载机保障战位分配的结果直接影响到舰载机保障的完成时间。

本文将以“福特”级航母为研究背景，航母甲板平面示意图如图1 所示。这里将对所求解的问题进行简化，仅考虑单一舰载机机种的情况。假设甲板右侧有12 个舰载机机位（按逆时针顺序，将这些机位依次标号为S1～S12战位），一般情况下，这12 个机位都停放着舰载机。当接收到一波次出动4 架舰载机的任务时，会从12 架舰载机中任意出动4 架，但因保障资源的限制，为了尽可能缩短保障完成时间，这4 架舰载机的选取需要根据保障任务提前予以预测。本文将从12 架舰载机中选取4 架出动的问题进行转化，即转化为从12 个机位中选出4 个，然后将待出动的4 架舰载机停放到这4 个被选中的机位上，最后，在确定保障战位的基础上制定最佳保障作业调度方案，其中4 个保障战位的选择即为舰载机的保障战位分配问题。

图1 “福特”级航母甲板平面示意图Fig. 1 Deck layout of Ford class aircraft carrier

1.2 保障作业调度

如图2 所示，基于“福特”级航母的舰载机保障流程，每架舰载机在滑出机位前都要完成图2中所示的全部保障任务。本文中的保障任务大致分以下为3 类：

图2 舰载机保障任务流程图Fig. 2 Flow chart of carrier-based aircraft support tasks

1） 并行任务，即一架舰载机在同一时间可以同时执行的任务。本文保障任务中的并行任务对包括供电和通风、充氧加油、军检挂弹、特设外观检查、航电外观检查以及机械外观检查。

2） 串行任务，指执行顺序不可交换且不能同时执行的任务。这些任务可以看做是拥有不同的优先级别，例如供电与通风的任务优先级最高，需要最先执行，检查验收任务的优先级最低，需要最后执行。

3） 顺序可交换任务，即在一架舰载机的保障作业中，执行顺序可以交换但不能同时执行的任务。如图2 所示，虚线连接的充氧和加油这2 个任务的执行顺序可以交换，但若是同时加油、充氧可能会造成事故，因此，加油和充氧这2 个任务一定有执行的先后顺序。

1.3 保障资源约束分析

影响一波次出动舰载机保障完成时间的因素有很多，其中最重要的是保障资源约束，包括保障班组的数量以及不同班组的保障任务完成时间。本文保障作业中的保障资源约束如表1 所示。

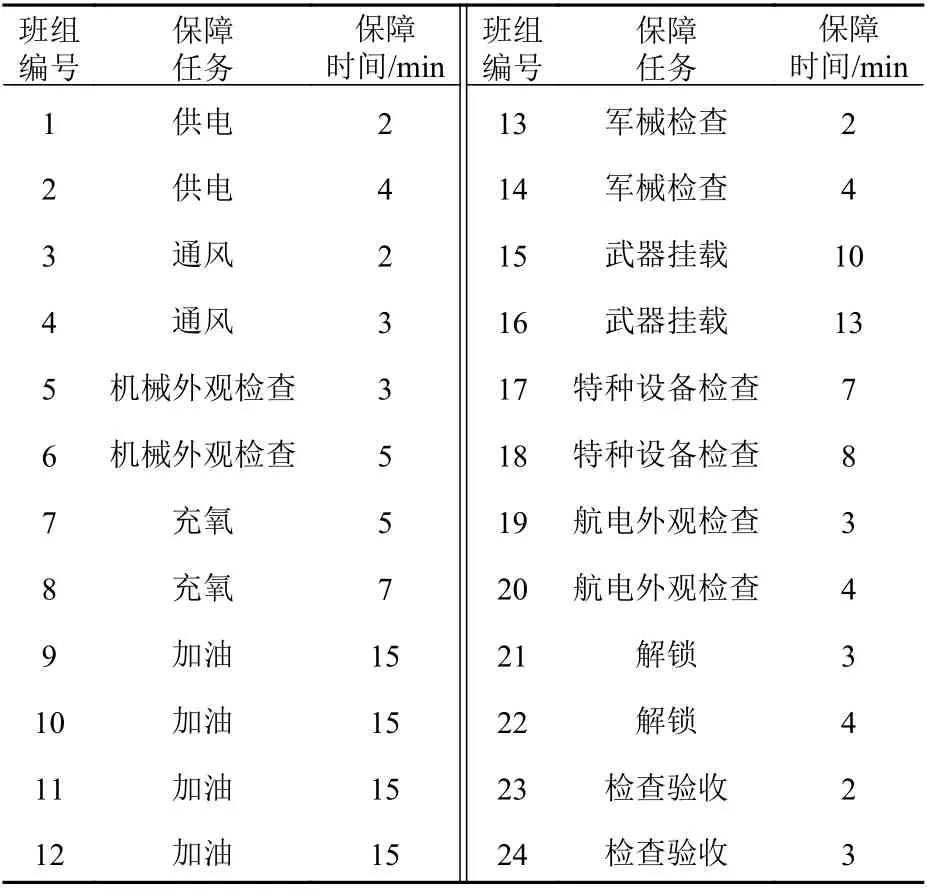
表1 保障班组任务执行时间表Table 1 Task execution schedule of the supporting teams

1.1 节中介绍的加油站的位置约束可以描述为如表2 所示，表2 中加油站的加油保障任务由表1 中的9～12 号班组完成。其中，S4机位可使用9 号或10 号加油站，S7机位可使用10 号或11 号加油站，S10机位可使用11 号或12 号加油站进行加油任务，其他机位固定，只能使用一个加油站。

表2 加油站位置约束Table 2 Constraint of gas station location

1.4 保障调度模型建立

本文研究问题的数学模型建立如下。

1） 目标函数。最小化一波次出动舰载机的保障作业完成时间，定义为：

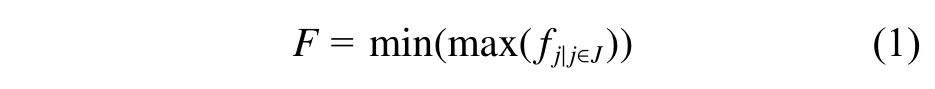
式中：fj为 保障舰载机j的完成时间；J为舰载机（保障战位）集合目标函数；目标函数F指最后完成的舰载机保障作业时间最短，从而实现一波次保障完成时间最短。

2） 约束条件。

（1） 对舰载机j的保障作业完成时间是其全部保障任务完成时间中的最大值。

式中：fi j为 舰载机（保障战位）j的保障任务i的完成时间；Oj为 舰载机j包含的保障任务编号集合。

（2） 每架舰载机的所有保障任务都只需要一个保障班组完成。

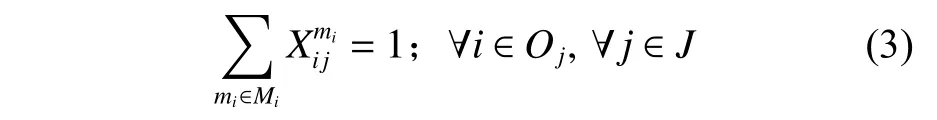
式中：mi为 执行保障任务i的保障班组编号；Mi为能够执行保障任务i的保障班组编号集合；为描述保障班组和保障任务对应关系的二元决策变量，如果将保障战位j分配给保障班组mi执行，则结果为1，否则为0。

（3） 保障班组在战位之间的移动时间与战位间隔成正比。

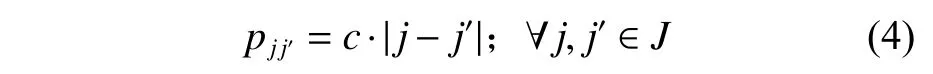
式 中：pj j′为 保 障 班 组mi完 成 保 障 舰 载 机j的 任 务后，转移到舰载机j′的时间；常数c为保障班组在相邻2 个战位间移动的时间。

（4） 在任意时刻每个保障班组只能执行1 架舰载机的1 项保障任务。

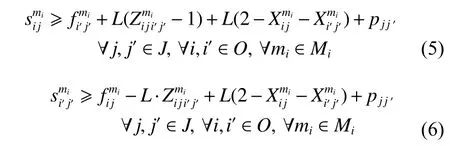
（5） 保障班组mi并非一直处于执行任务的状态，需要考虑其在战位间的移动时间。

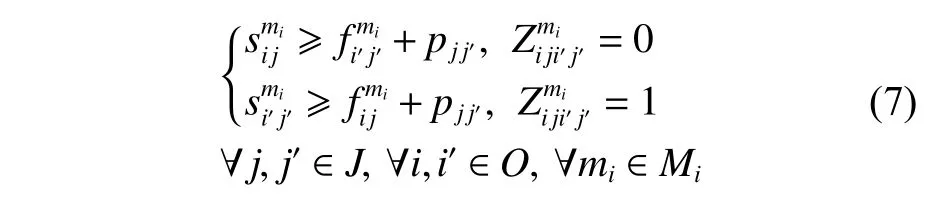
（6） 每个保障任务都有一定的时长，保障任务在执行的过程中不能被打断。

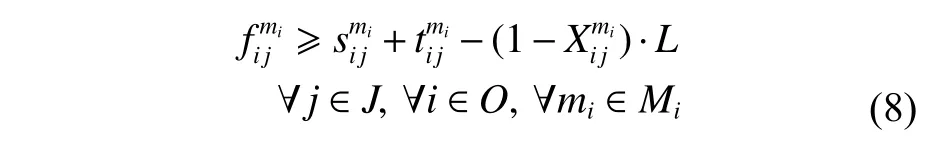
（7） 开始执行一项保障任务前，要确保其所有紧前任务均已完成。这是因为保障流程中存在并行任务，某项任务可能会有多个紧前任务，所以选取紧前任务集合中完成时间最长的作为标准。

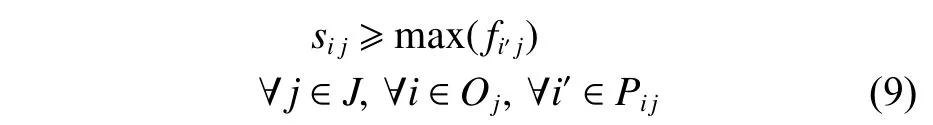
式中，Pi j为保障任务Oi j的紧前任务集合，其中Oi j为舰载机j的保障任务i。

（8） 舰载机保障流程中存在保障顺序可以交换的保障任务，但是这些任务不能同时执行。

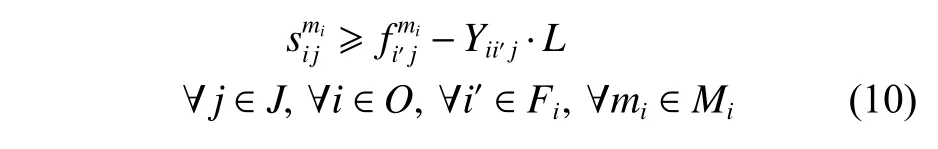
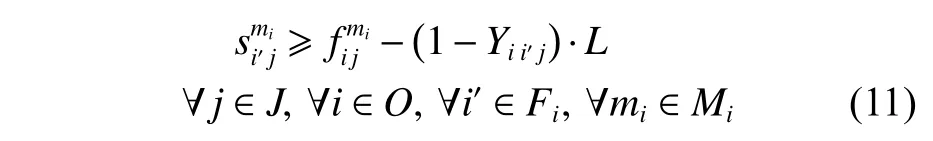
式中：Fi为可保障任务i顺序可交换的保障任务集合；Yii′j为描述舰载机保障任务顺序的二元决策变量，如果保障舰载机j的任务i先 于任务i′执行，则结果为1，否则为0。

（9） 加油站条件约束，即每个战位执行加油保障时，只需一个加油站供油。

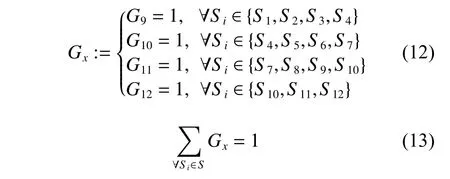
式中：Gx为描述编号为x的加油站使用情况的二元决策变量；Si为保障战位编号；S为保障战位集合。

2 专家示例样本集及分类器构造

2.1 基于成对比较模型构造的样本集

本文中用于解决保障战位分配和保障作业调度问题的方法，受益于Gombolay 等[9-10]基于VMPTR提出的学徒制算法，该算法旨在学习专家所做的示例，就像学徒模仿专家行为一样。目前，向专家示例学习（learning from human demonstrations，LFD）[15-16]是机器学习领域的一大热门。同时，本文还从Page 等[17]提出的网页排序算法中总结出了成对比较模型，并将其应用于学徒制算法中。使用已执行任务与未执行任务组成的成对比较模型构造样本集，同时使用该样本集训练分类器，最终建立学徒制算法，进而求出调度问题的最优解。

假设给定的专家示例是问题的最优解，对于每个专家示例，可以构造一个时序的状态观测集Ω={Ω1，Ω2，···，Ωs}。 通过观测集 Ω可以很容易地得出，在状态观测 Ωm中 ，对于AgentAi（即保障班组i）来说，最优的待执行任务即为 τi，但却无法得知任务集中各任务间的关系。由此，本文通过将状态观测 Ωm中 选定执行的 τi与任务集中剩下的所有未执行任务进行两两对比来构造样本集。

从给定的专家示例中选取全部的任务构成任务集 τ(τi∈τ)， 任务集中的每个任务 τi都有一个描述任务特征的实值特征向量 γτi，其由多个与调度问题相关的特征组成。例如，任务的截止时间、最早可以开始执行任务的时间以及任务持续时间等，根据调度问题的不同，这些特征的选取也不同。总之，被选出来的特征应该是最能够表现出任务重要程度的。

状态观测 Ωm由以下2部分组合而成：1）描述各任务状态的特征向量γτ={γτ1,γτ2,···,γτn}；2）专家示例中ti时 刻执行的任务 τi（包括Agent 空闲时的 τ0） 。在状态观测 Ωm中，将专家示例中已经执行的任务 τi作为模本，将剩下的所有未执行的任务τj依次与 τi进行比较，从而获得相关模型的参数以及用来训练模型的样本集。

对于将选中的任务 τi与 未选中的任务 τj进行成对比较的方法，其旨在向专家示例学习并通过分析任务状态，以此确定下一个待执行任务的策略，最终通过迭代得到一个完整的调度计划。为达此目的，首先将状态观测 Ωm转换成一个由选中任务 τi与 未选中任务 τj进行对比得到的新观测，如式（14）和式（15）所示。式（14）为每个状态观测构造了一个正例样本，其中包括输入特征向量和 一个正标签=1， 输入特征向量的每个元素由描述选中任务 τi状态的 γτi和描述未选中任务 τj状态的 γτj相减得到。式（15）为每个状态观测构造了一个负例样本，由输入特征向量和负标签=0组合而成，其中输入特征向量由 γτj与 γτi相减得到。

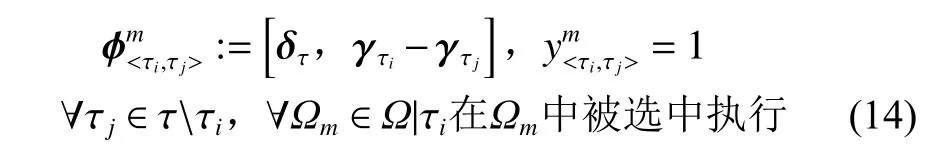
考虑到不同问题的环境因素对调度计划的影响，引入了描述环境特征的向量 δτ。 由于 δτ对同一问题下的每个任务都是一样的，如果将 δτ放入γτ中 ，在构造样本集时， γτi与 γτj相减就互相抵消了，因此在输入特征向量中单独加入了 δτ，如式（14）和式（15）所示。

得到t时刻应进行保障作业的战位后，需将此战位负责的任务分配给特定的保障班组。同时，还需预测在t时刻保障班组AgentAi应执行选出的任务，还是执行任务 τ0（ 空任务），即Ai空闲。式（16）和式（17）提供了此分类器的训练样本集。输入的特征变量act由环境特征向量 δτ和描述选中任务τi的 状 态 向 量 γτi构 成。i为 样 本 标 签，AgentAi执行选出的任务 τ*i时，=1； AgentAi执行空任务τ0时 ，=0。

2.2 舰载机保障调度问题特征选取

Cheng 等[18]和 Raghavan 等[19]针对利用专家判断方式选取特征进行过研究，本文也将采用类似方式。

图3 所示为专家示例中的保障作业调度甘特图。在该示例中，4 架舰载机均为同一类型，也即保障作业流程相同，保障战位分配结果分别为S4，S7，S10和S11，最长保障完成时间为42 min，保障作业流程如图2 所示。图3 中，矩形内的标签分别表示舰载机编号和保障工序编号，图中灰色部分表示保障班组在战位之间的移动时间（后文同此）。

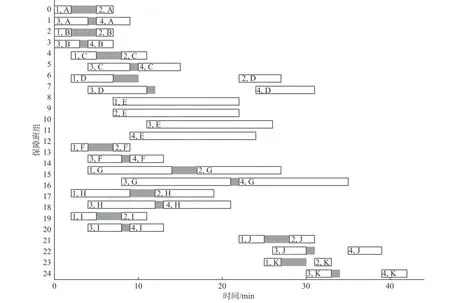
图3 专家示例中保障作业调度甘特图Fig. 3 Gantt chart of support task scheduling in expert demonstrations

表3 和表4 所示均为根据专家示例中保障作业调度方案列举的特征值。其中，表3 所示为t=0时 刻的环境特征，表4 所示为t=0时刻Agent 1选择执行1 号战位（S4）的任务特征，此时1 号战位即为被选中的任务 τi。

表3 t=0 时刻的环境特征Table 3 Environmental features at t=0

表4 t=0 时刻Agent 1 选择执行1 号战位（S4）任务的特征Table 4 Features of Agent 1 chooses to execute task of 1# action station (S4) at t=0

2.3 分类器训练

采用分类器算法学习专家在保障战位分配、作业分配等方面的经验。本文将使用决策树（DT）、K-近邻（KNN）、支持向量机-径向基函数（SVM-RBF）、逻辑回归（LR）、朴素贝叶斯（NB）以及随机猜测（RG）这6 种算法来分别训练用于舰载机战位分配的分类器fpriority_site(τi,τj)、保障作业分配的分类器fpriority_schedule(τi,τj)和判断任务能否执行的分类器fact(τi)。 对于分类器fpriority_site(τi,τj)，通过已有的专家示例构造了4930条样本作为其样本集，分类器fpriority_schedule(τi,τj)和fact(τi)的样本集中包含的样本数量分别为3 000 和1 500。为了得到稳定、可靠的分类器模型，本文使用样本集中85%的样本作为训练集，剩余的15%作为测试集对模型进行了评估。

对于分类器的选取，采用灵敏度（又称“真阳性率”）和特异度（又称“真阴性率”）这2 个指标进行评估，如图4 和图5 所示。最终，选择SVMRBF 算法和DT 算法分别训练出了保障战位分配分类器及保障任务分配分类器。

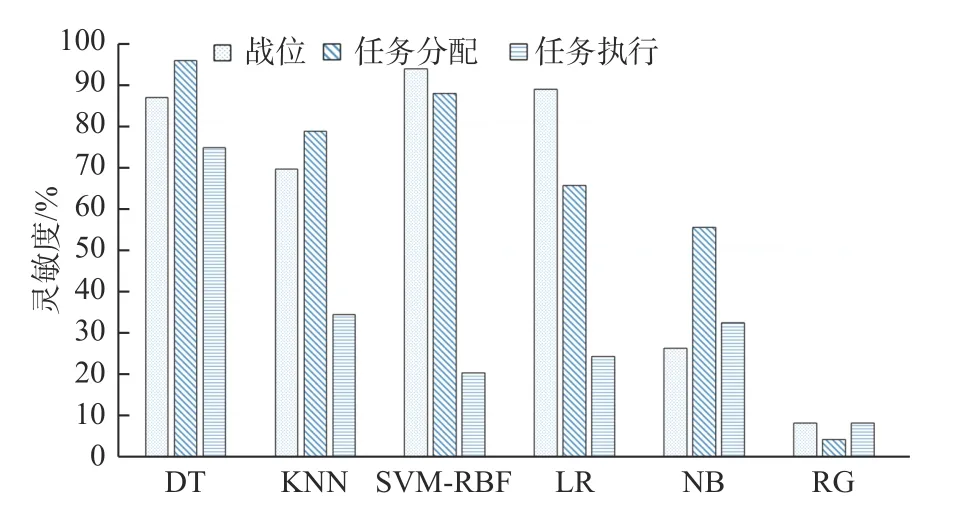
图4 使用不同机器学习算法训练的3 个分类器模型的灵敏度Fig. 4 Sensitivity of three classifier models trained by different machine learning algorithms

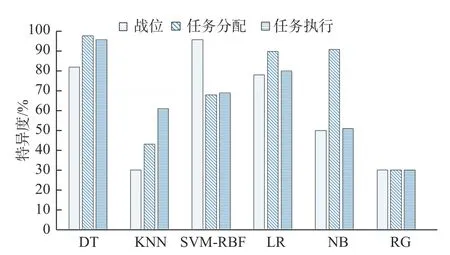
图5 使用不同机器学习算法训练的3 个分类器模型的特异度Fig. 5 Speifiity of three classifier models trained by different machine learning algorithms

3 基于学徒制舰载机保障调度算法设计

首先，分析已有的专家示例，将t时刻AgentAi选择执行的任务 τi与剩余未执行的任务 τj两两对比，获得学徒制调度算法的分类器样本集；然后，使用机器学习算法训练分类器。有关样本集和分类器的构造上节已详细介绍。

使用学徒制调度算法解决新问题的基本原理如下：首先，在新问题的任务集τ （ 含有n个任务）中随机选取一个任务 τi作 为AgentAi下一步要执行的任务，剩余的任务依次作为 τj，将 τi和 τj两两组合作为分类器fpriority(τi,τj)∈{0,1}的输入，该过程如图6 所示；然后，将得到的n-1个结果求和并储存到数组H 中，重新选取新的 τi并重复以上步骤，直至无新的 τi可以选取后，再遍历数组H 找到其中最大的元素hmax，hmax对 应的任务 τi即为新问题中AgentAi下 一步要执行的任务。式（18）表示在新问题的成对模型中，具有最大累积优先级的结果即为AgentAi下 一步要执行的最佳任务。

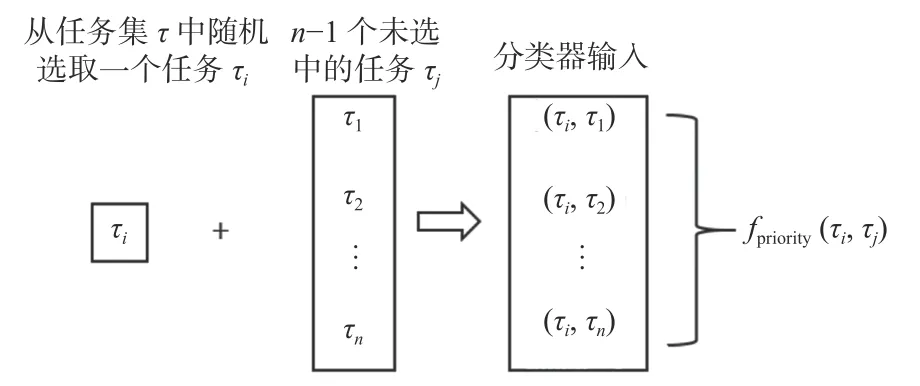
图6 分类器 fpriority(τi,τ j)的输入构成示意图Fig. 6 Schematic of input structure of classifierfpriority(τi,τ j)

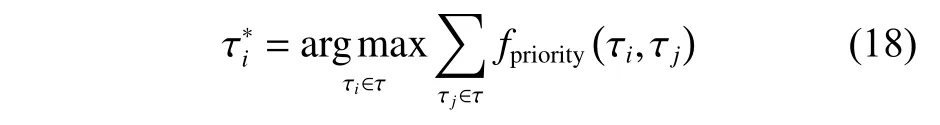
学徒制调度算法的基本步骤如下：

1） 算法的初始化。将战位分配方案集 τsite、保障班组集A、时间约束集（例如，舰载机最晚起飞时间T、每项任务保障时间等）以及顺序可交换的保障任务集作为算法的输入；

2） 通过保障战位分配方案的成对模型，得到分类器累积优先级最大的结果，即为第1 个子问题的解，并将其作为第2 个子问题的输入；

3）在t时刻，对AgentAi来说，具有最高累积优先级的即为当前保障班组Ai此时应保障的战位；

4） 通 过 分 类 器fact()∈{0,1} 判 断 在t时刻保障班组Ai能 否保障战位，若结果为1，将该保障任务加入调度计划表中，若结果为0，则将 τ0（空任务）加入调度计划表中；

5） 判断在t时刻全部保障班组是否都已安排任务，已完成则继续步骤6），若还没有，则对未安排任务的保障班组重复步骤3）～5）；

6） 判断当前时刻t是否为起飞时刻T，若是，则表示已完成调度计划并将其输出，若不是，则更新t为下一时刻，重复步骤3）～6），继续进行下一时刻的调度计划。

4 仿真实验及结果分析

4.1 仿真实验结果

假设一波次出动的舰载机数量为6 架，使用本文设计的学徒制调度算法来获取6 架舰载机的最佳保障战位分配结果，同时确定最优保障作业调度计划，以使该波次的舰载机总体保障完成时间最短。保障作业调度计划甘特图如图7 所示。

图7 采用学徒制调度算法所得保障班组甘特图Fig. 7 Gantt chart of supporting teams solved by apprenticeship scheduling algorithm

通过采用学徒制调度算法求解该实例问题，得到6 架舰载机最优保障战位分配结果分别为S3，S4，S5，S7，S10，S11，班组工作排布结果显示，最长保障完成时间为60 min，保障班组平均移动时间为5.5 min，可同时使用2 个加油站的战位数量为3 个。该结果与人工排布策略相契合，即在尽可能缩短保障完成时间的同时，提高了加油站的使用效率。可见，通过向专家示例（图3）学习，使用学徒制调度算法可仿照专家排布策略求解新问题。

4.2 对比试验

4.2.1 分类器性能对调度结果的影响

由分类器构造过程可知，分类器性能受专家示例构造的样本数量和质量的影响，为弄清楚样本的数量与质量对学徒制调度算法性能所造成的影响，设计了基于4.1 节所述保障调度问题的对比实验。使用数量为原始样本集的50%、正确率为80%的样本训练出的新分类器，然后使用新的分类器重新设计算法，最后针对新的实例问题再次求解。所得舰载机保障调度结果如图8 所示。

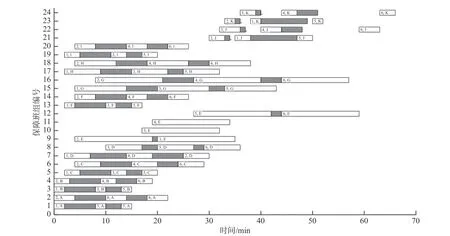
图8 采用样本数少、质量低的学徒制调度算法所得保障班组甘特图Fig. 8 Gantt chart of supporting teams solved by apprenticeship scheduling algorithm with few and low quality samples

由图可知，6 架舰载机的最优保障战位分配结果为S1，S2，S7，S8，S10，S12，班组工作排布结果显示，最长保障完成时间66 min，保障班组平均移动时间（以下称平均移动时间）7.7 min，可同时使用2 个加油站的战位数量为2 个。

4.2.2 基于遗传算法求解的实验结果

为了验证学徒制调度算法与传统算法相比更适于求解保障作业调度，本文将遗传算法作为传统搜索算法的代表，使用该算法针对新的问题重新进行了求解。遗传算法在迭代过程中适应度最大的个体对应的最终保障完成时间如图9 所示。

图9 遗传算法迭代曲线Fig. 9 Iterative curve of genetic algorithm

图10 所示为使用遗传算法对新的实例问题进行10 次求解后所得最优保障班组甘特图。由图可知，其最优保障战位分配结果为S3～S8，最长保障完成时间62 min，平均移动时间3.5 min，可同时使用2 个加油站的战位数量为2 个。

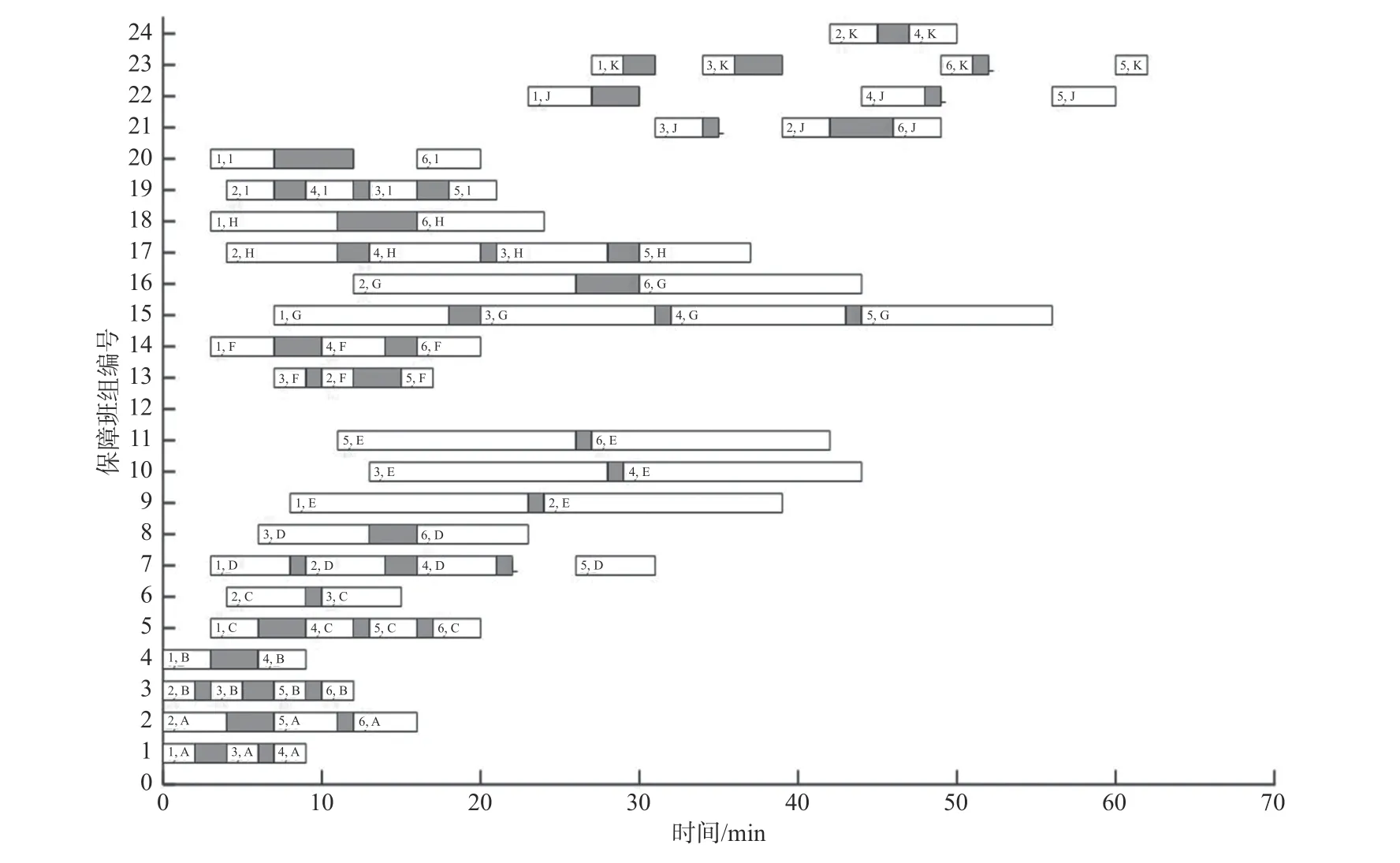
图10 采用遗传算法所得保障班组甘特图Fig. 10 Gantt chart of supporting teams solved by genetic algorithm

4.2.3 实验结果对比分析

表5 所示为针对4.1 节中新的舰载机保障调度问题，采用3 种算法进行多次求解并取平均值后的汇总结果。

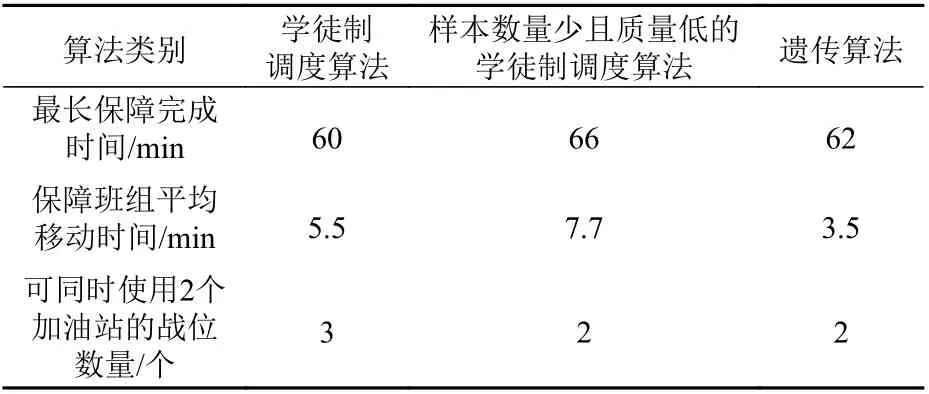
表5 3 种算法对舰载机保障调度问题求解结果对比Table 5 Comparison of the solutions of three algorithms to aircraft support scheduling problem

1） 保障总时间对比。

遗传算法是目前应用最普遍的智能搜索算法，它搜索全局最优解的能力很强。对于舰载机保障调度问题，采用学徒制调度算法所得解的最长保障完成时间少于遗传算法，这说明学徒制算法的求解效果略优于遗传算法。而采用样本数量少且质量低的学徒制调度算法所得解的保障总时间是3 种算法中最长的，这说明样本的数量和质量会极大地影响解的质量。

2） 保障资源利用情况对比。

采用遗传算法所得保障战位分配结果使得其保障班组平均移动距离与学徒制调度算法结果相比大幅减少，这意味着保障班组处于空闲状态的时间比较短，保障工序之间衔接的更加紧密，但这种战位分配方案却导致1 号加油站不可用，反而增加了其他保障班组的工作量，使得工作分配不均，整体保障完成时间延后。但采用样本数量少且质量低的学徒制调度算法得出的解则大大延长了保障班组的平均移动距离，在实际场景中，更易受到甲板空间的限制。

另外，使用学徒制调度算法所得加油站的分配方案相比遗传算法更为合理，能够更多地安排可以使用2 个加油站的战位。当舰载机数量增多时，采用这种策略可以减少等待时间。

3） 求解时间对比。

采用遗传算法时收敛速度较慢，其计算时间约为学徒制调度算法的4.5 倍。另外，学徒制调度算法的分类器是提前学习好的，可以作为离线工具，在实际运用时无需计入学徒制调度算法的求解时间，从而避免了求解资源的浪费。并且，随着样本数的增加，还可以不断更新。

5 结 语

学徒制调度算法相比常见的智能搜索算法更适用于求解舰载机保障作业调度问题。学徒制调度算法分类器的分类质量依赖于样本数量和质量，当专家示例规模简单或不具备最优性时，就不能保障所提取样本集的数量和质量，其性能会大打折扣，且解的质量也会随之降低。目前，学徒制调度算法仅限于静态、单目标的舰载机保障调度问题，下一步将针对动态、多目标的新场景和新问题开展研究。