基于交互式多模型平方根容积卡尔曼滤波的船舶轨迹跟踪
2022-09-06杨家轩陈柏果马令琪
杨家轩,陈柏果,马令琪
1 大连海事大学 航海学院,辽宁 大连 116026
2 辽宁省航海安全保障重点实验室,辽宁 大连 116026
0 引 言
智能航运是海运业未来的发展方向,船舶在航行的过程中要求其能自主探测其他船舶并采取适当的规避措施。探测其他船舶的移动,可以使用各种导航传感器,如自动识别系统(AIS)、航海雷达和激光雷达。其中,AIS 适用于所有300 总吨以上的船舶和许多小型船舶,其允许船舶广播自己的位置、航向和时间数据,并接收附近其他船舶的信息,可提高海上航行的安全和效率。同时,由于AIS 是通过甚高频无线电频率来进行传输,即使是在雷达探测受到威胁的恶劣环境中,其也能继续探测其他船舶,因此,AIS 被广泛用于电子海图集成显示、船舶的监控调度、港口交通流规律的挖掘等领域。
然而,若要通过AIS 获取准确、可靠的信息,特别是实时位置和航速等动态信息,仍然存在一些问题。Banyś等[1]针对实际情况下AIS 数据的长期分析表明,因AIS 中的部分数据被设置为默认值,或其数据帧严重违反指定的更新速率,导致许多AIS 消息中包含有不可信的位置坐标。此外,AIS 的参数,如航向或航速有可能是由错误的位置估计得出,从而导致了虚假的船舶动态状态信息。
AIS 最初被设计为仅用于交换静态数据和导航数据,不提供任何完整性信息,因此不能确保服务的连续性。AIS 信息有时会被部分或完全中断,并且因“数据干扰”问题导致的数据丢失在高流量区域可能会更严重[2]。
目前,卡尔曼滤波(KF)算法常被用来进行机动目标的跟踪和导航,如扩展卡尔曼滤波(EKF)[3]、无迹卡尔曼滤波(UKF)[4]、容积卡尔曼滤波(CKF)[5]等。为确保AIS 信息的可靠性以及数据的精度,可以采用卡尔曼滤波算法对AIS 数据进行处理。Jaskólski[6]采用传统的KF 算法估计了AIS 报告的位置坐标,但该方法仅适用于船舶航行的线性环境,在非线性情况下(如转弯操作)会产生错误警报。Perera 和Soares[7]采用恒定转向率模型(CTM)作为非线性状态估计量,假设船舶处于匀速状态,结合EKF 算法对船舶处于非线性环境下的航行轨迹予以了估计。Fossen 等[8]采用EKF 算法处理AIS 的实时数据,并将其用于了碰撞检测和实时可视化,但基于EKF 的预测算法只能考虑单一的船舶运动模型,难以描述变换状态的船舶运动。Fossen 等[9]又将船舶全局运动参数加入系统状态方程中,通过构建eXogeneous 卡尔曼滤波器(XKF),完成了对船舶运动模式的实时预测,但该模型在近180°的机动角度下预测轨迹存在较大误差。针对AIS 数据呈现的多机动性和运动模式多的问题,姜佰辰等[10]采用多项式卡尔曼滤波对数据进行了处理,但算法的轨迹跟踪效果取决于多项式的阶数,且缺乏性能的对比标准。Siegert 等[11]将交互式多模型(IMM)框架用于混合恒速过程模型和恒定转向率过程模型的状态估计,并结合EKF 算法对船舶的非线性状态估计进行了处理。但在采用EKF 对非线性函数进行近似化处理的过程中会引入较大误差,这对于强非线性滤波问题来说容易发散,故一般用于非线性程度低且初始误差较小的系统[12]。Liu 等[13]设计了一种使用KF和IMM 的智能鲁棒跟踪算法,该算法在受限的环境下依然能够利用AIS 数据中不完整的动态信息计算出精确的运动信息。于泽祥等[14]采用交互式多模型-平方根容积卡尔曼滤波( IMM-SCKF) 算法对海上扩展目标进行跟踪滤波,通过扩展信息,提高了算法的跟踪精度。但以上采用IMM 框架的方法没有考虑船舶或运动目标航速的变化及航向率的变化,对目标运动的描述还不够全面和准确。
在采用AIS 数据进行跟踪和预测的KF 算法中,使用较为广泛的是EKF 算法,但在船舶航向和航速变化较频繁的轨迹跟踪场景下,采用EKF算法会引入较大的误差。针对EKF 算法的稳定性问题,本文将引入一种更具数值稳定性的SCKF算法来进行AIS 数据的轨迹跟踪。根据船舶航向和航速的变化,可以划分出直线运动、转向运动和变速运动3 种基本运动状态,船舶的运动可以看作是这3 种运动状态的变换与组合。对于涉及这3 种运动状态的船舶轨迹,采用单一运动模型无法准确拟合和描述。而IMM 算法可以将多个模型进行融合并自适应转换表征目标的运动状态,因此,本文拟将SCKF 算法和IMM 框架相结合,通过IMM 框架对单一运动模型进行组合。首先,采用恒速直线模型(CVM)和恒定转向率模型(CTM)交互融合形成的组合模型与单一模型进行比较,验证IMM 框架的性能;然后,考虑轨迹航向的变化,采用转向率估计值来替代固定转向率以形成改进的CTM 模型,通过CVM 与改进的CTM 形成组合模型,分析改进的CTM 模型性能及其对存在转向率变化的船舶运动的表征能力;最后,针对存在直线运动、转向运动和变速运动的轨迹,采用CVM、当前统计模型(CSM)和改进的CTM 模型三者融合形成的组合模型进行跟踪实验,通过实验对比EKF和SCKF 算法的性能,分析不同组合模型的性能和使用场景,以验证本文算法对涉及2 种以上运动状态的船舶轨迹跟踪结果的准确性和稳定性,从而提高AIS 的服务质量。
1 AIS 数据的单位转换
AIS 数据包含对地航速V、对地航向φ以及地理位置的经纬度 (l, μ) 。 为便于计算,可将航速V的单位由kn 转换为 m/s。目前,AIS 数据的经、纬度是采用大地测量系统(WGS84)坐标系来进行记录,将经、纬度坐标映射为笛卡尔坐标 (x,y)。最后,坐标将使用二维笛卡尔坐标系来表示。
假设地球平面坐标原点位于经纬度(l0, μ0)处,并定义
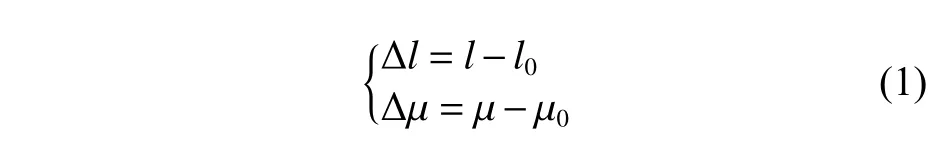
地球在垂直主子午线上的曲率半径RN和在子午线上的曲率半径RM由式(2)表示:
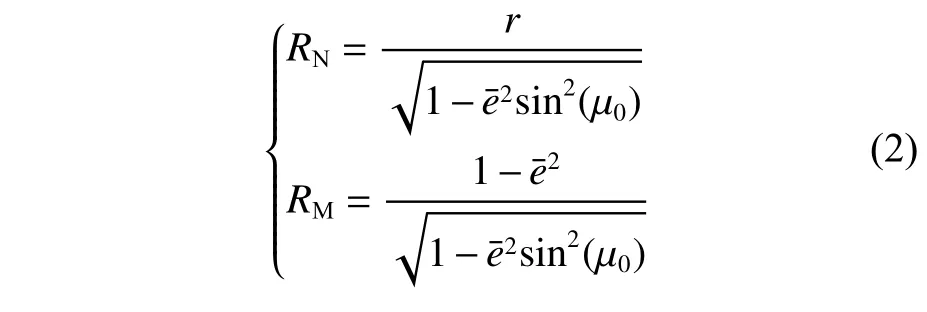
式中:r为半短轴(赤道半径),r=6 378 137 m;e¯ 为地球偏心率[8],e¯=0.081 8。笛卡尔坐标系下的位置 (x,y)的计算如下:
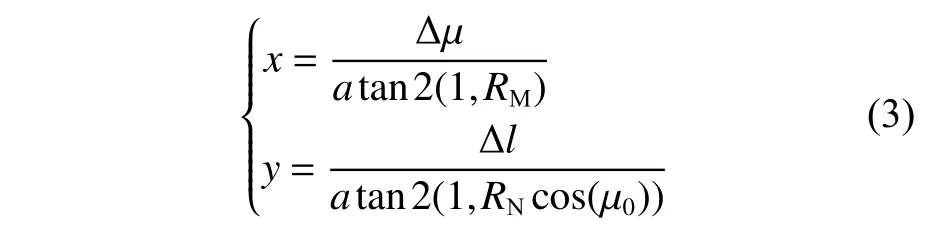
式中,atan2(y,x)为四象限反正切,将结果限制在[-π,π]范围内。
2 船舶运动模型
由于大多数船舶既没有很强的机动性,也不能在一定的采样周期内快速改变改变航速,因此,使用简单的运动模型来表示船舶的运动是合理、可行的。在模型选择过程中,考虑了能够捕捉船舶运动能力的二维运动学模型[7]。假设船舶是一个质点,忽略其尺寸。如图1 所示,船舶位于点A 处,船舶的位置坐标由连续时间内的x和y来表示;vx,vy为 船舶沿X,Y方向的连续时间速度分量;v为船舶的航速;v˙为船舶航速的变化率; 假设船舶对地航向与船艏航向一致,则 ω为船舶航向的变化率;x(t),y(t)为 船舶在笛卡尔坐标系下时间t处的位置;an,at分别为船舶的法向加速度和切向加速度[7]。

图1 船舶运动模型示意图Fig. 1 Schematics of ship motion model
曲线运动模型可用于描述船舶运动:
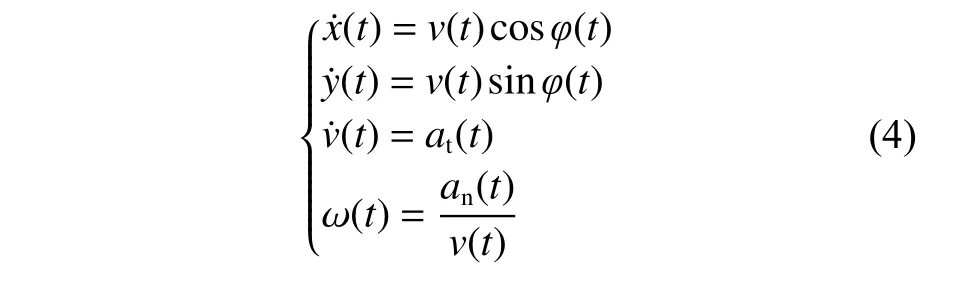
式中, ω(t)为 船舶在笛卡尔坐标系下时间t处的航向变化率。从该船舶运动模型中,可以观察到一些重要的运动特征。基于式(4),可推断有3 种不同的运动状态:
1)an(t)=0,at(t)=0,直线匀速运动;
2)an(t)=0,at(t)≠0,直线变速运动;
3)an(t)≠0,at(t)=0,转向匀速运动。
当an和at均为0 时,船舶匀速直线运动。假设航速在第k个采样周期内有一个恒定值,则CVM模型将被用来描述船舶的直线匀速运动。设采样周期为T,则CVM 模型的离散状态方程为[15]:
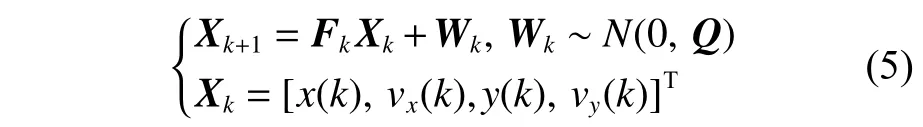
其中:

式中:Xk为 状态向量;Fk为 状态转移矩阵;Wk为过程噪声,其服从均值为0、协方差矩阵为Q的正态分布;q为过程噪声的协方差系数。
当an(t)=0,at(t)≠0时,船舶直线变速运动。本文采用CSM 模型来表示船舶的直线变速运动。CSM 模型是一种非零均值时间相关的模型,其假设目标以某一加速度机动时,下一时刻的加速度取值范围有限,且总在“当前”加速度值的附近。这种对于船舶航速变化状况的描述是较为合理的。CSM 模型的离散状态方程为[15]:
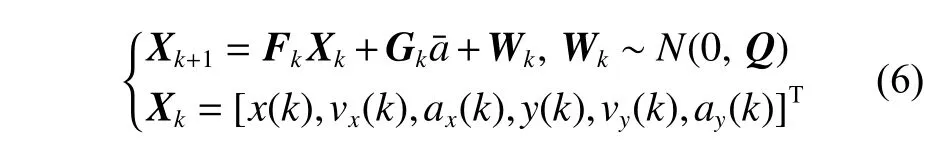
其中:

式中:ax(k),ay(k)分 别对应于X,Y轴方向上的加速度;a¯为 加速度的均值,通过矩阵Gk进 行更新; α为机动时间常数;q11~q33的表达式参见文献[7];σa为加速度的方差。

式中:amax为目标的最大正向加速度;a-max为目标的最大负向加速度;a¯(k)为加速度的均值,当前加速度的均值取加速度的估计值。
当an(t)≠0,at(t)=0,时,船舶进行圆周匀速运动,也即转向运动。假设在第k个采样周期内船舶的航速和角速度恒定,此时船舶的运动过程适合采用CTM 模型来描述。CTM 模型的离散状态方程为[15]:
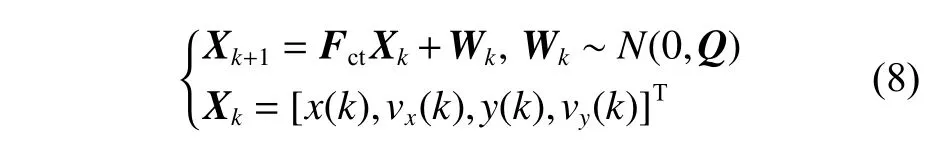
其中:
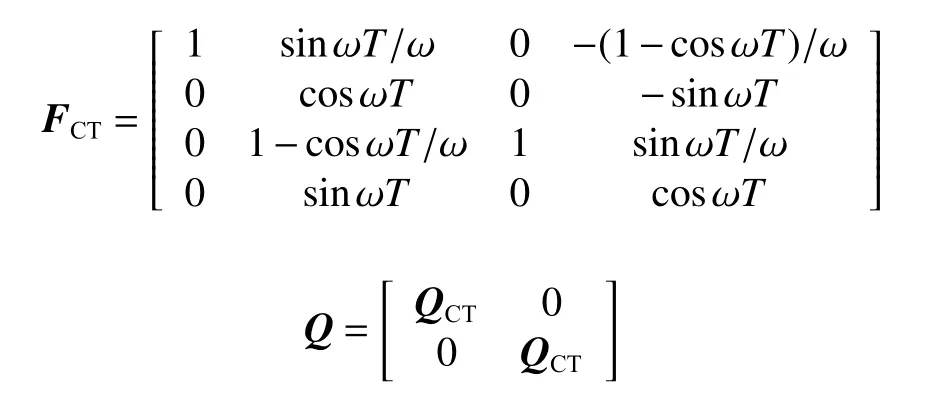
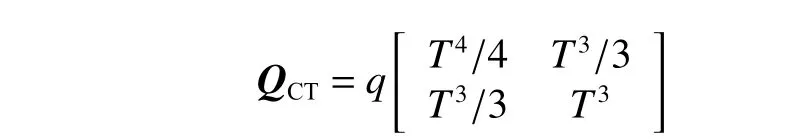
式中, ω为航向的变化率。
CTM 模型性能受转向率的影响较大。在准确了解转向率的情况下,CTM 模型能提供良好的跟踪性能。在极少数情况下,恒定的转向率是预知的,但在大多数实际情况下,直接使用CTM 模型不现实。因此,一个自然的想法就是用其估计值 ω˜来代替。需要注意的是,应当筛选估计值以降低异常值的影响。利用饱和函数 sat(ω)来确保|ω˜|≤ωmax,以防止估算的转向率超出转向率最大值 ωmax,可增加AIS 测量数据的鲁棒性。

3 基于AIS 的船舶轨迹跟踪算法
3.1 SCKF 算法
在自主或辅助导航领域,KF 算法已经得到广泛的研究和应用。而EKF 算法则被认为是许多非线性系统应用的标准方法,其能够使系统关于估计的状态轨迹线性化。然而,这会导致稳定性问题。另外,在采用EKF 算法对非线性函数进行近似化处理的过程中会引入较大误差,它只在非线性动态系统与观测模型的线性近似有效的情况下才表现良好。Duan 等[16]提出了SCKF 算法,该方法是以目标状态协方差的平方根来进行迭代更新,可确保滤波过程中协方差矩阵的对称性和半正定性,能够改善数值的精度和稳定性。本文将SCKF 算法与IMM 框架相结合,能够对不同维数的模型进行交互滤波,更适合解决船舶在含有多种运动状态场景下的动态滤波问题。
如图2 所示,AIS 数据传输机制由2 部分组成:数据接收点和数据等待期[2]。导航信息在每个数据接收点传输,在数据等待期中则没有信息的传输。并且,AIS 是根据船舶的航速以不同的更新速率来传输动态信息的,这会导致不同类型的AIS 数据的数据接收点间隔时间不一致。

图2 AIS 传输机制图Fig. 2 AIS transmission mechanism
本文中,SCKF 算法的迭代运算过程采用离散时间形式的预测-校正表示法[17]描述。两个数据接收点之间的采样时间将随着船速的增加而自动减少,如果船舶正在做机动航行,信息间隔会进一步减少。因此,可以选择采样时间的倍数来作为校正器的更新时间。
船舶过程方程的离散形式可由式(5)、式(6)和式(8)来表示。船舶测量模型的离散形式为:

式中:Zk+1|k为测量的状态向量;h(Xk+1)为测量函数;Vk为具有零均值和测量噪声矩阵R(k)协方差的白高斯测量噪声。
本文所采用的3 种船舶运动模型的测量函数均可采用下式表示:

基于过程方程和测量方程,采用预测-校正表示法的SCKF 算法的步骤如下所示。
步骤1:初始化。
步骤2:预测过程。
计算状态容积点及其对应的权重:
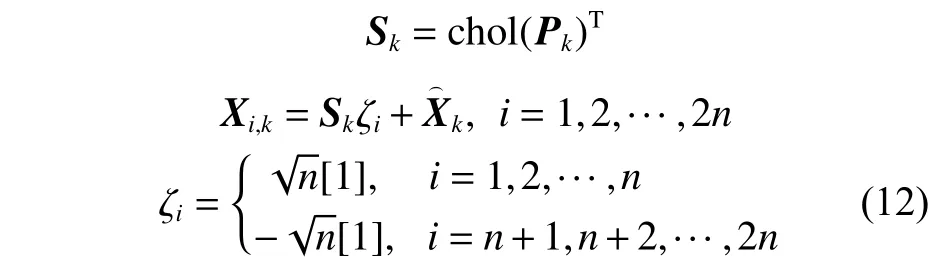
式 中:Pk通 过Cholesky 分 解 得 到 平 方 根Sk; ζi为第i个容积点;n为系统状态向量的维度; [1]为单位矩阵。每个容积点的权重为。
传播状态容积点:
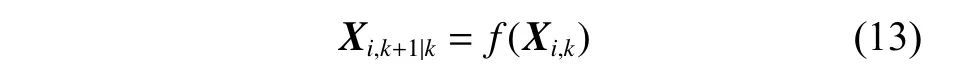
式中:f(Xi,k)为 系统过程函数;Xi,k+1|k为每个容积点对应的预测值。
计算状态向量预测值:

计算状态误差协方差的平方根的预测值:
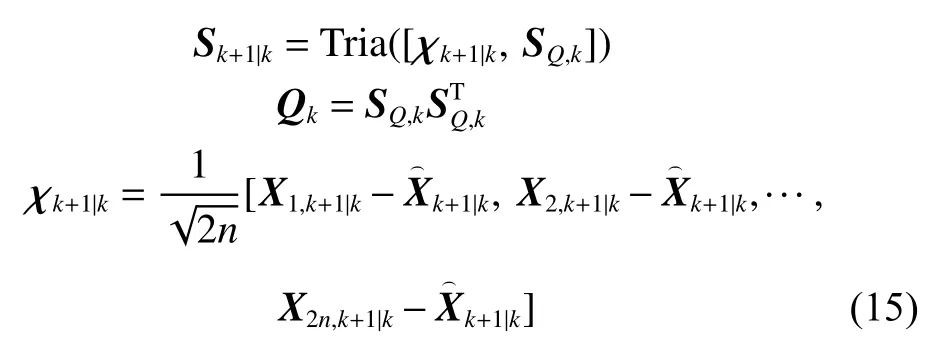
式中:Sk+1|k为一个下三角矩阵; Tria(*)为矩阵的正交三角(QR)分解;Qk为过程噪声的协方差矩阵,其平方根形式为SQ,k; χk+1|k为状态向量的偏差矩阵。
步骤3:校正过程。
计算测量容积点及其权重:
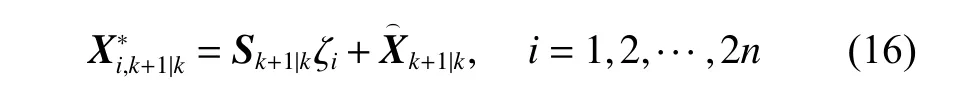
计算通过测量方程传播的容积点:

计算测量状态的预测值:

计算测量误差协方差的平方根:
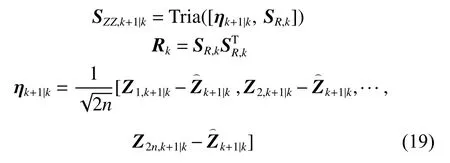
式中:SZZ,k+1|k为新息方差的平方根因子; ηk+1|k为测量向量的偏差矩阵;Rk为测量噪声的协方差矩阵,其平方根形式为SR,k。
计算互协方差:
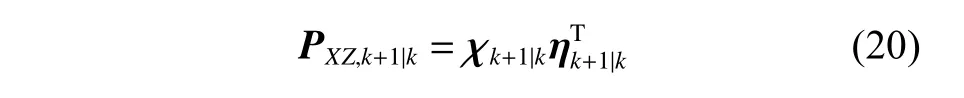
更新卡尔曼增益:

更新状态值:
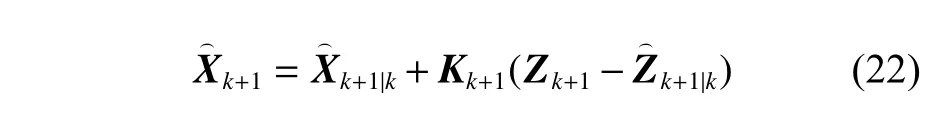
更新状态误差协方差的平方根:
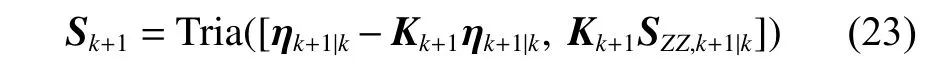
3.2 IMM-SCKF 算法
尽管对所有动态场景只使用一个模型是可以接受的,但若能将不同模型的优势都融合到一个组合过滤器中,这对复杂船舶运动轨迹的拟合和描述来说效果将更好,能扩展跟踪算法的适用场景并提高跟踪算法的稳定性和精度。与其他利用多个模型并行运行的方案形成对比的是,IMM 混合了不同模型的状态估计,而不用在一个或另一个之间做出艰难的决定。
图3 描述了IMM-SCKF 算法原理。SCKF 滤波器分别采用CVM,CSM 和改进的CTM 这3 种模型来实现状态的估计与更新,IMM 框架则将通过滤波器得到的状态进行交互融合。IMM-SCKF算法的推导步骤如下所示。

图3 IMM-SCKF 算法的原理框图Fig. 3 Block diagram of IMM-SCKF algorithm
步骤1:输入交互。
考虑N个运动模型,假设上一次迭代运算的第j个模型对应的状态向量和误差协方差矩阵分别为以及。在SCKF 算法的每个预测-校正周期之前,通过输入的交互融合得到第j个滤波器的初始状态向量和初始误差协方差矩阵。
步骤2:模型过滤器。
用N个滤波器来表示N个运动模型(本文中,N=3) ,将在步骤1 中获得的和作为SCKF算法的初始输入,用k+1时 刻的测量值Zk+1来进行校正。最终,滤波器得到的状态向量和误差协方差矩阵的估计分别为和1。
步骤3:更新模型概率。
步骤4:输出交互。
将滤波得到的结果进行交互融合,从而得到最终的预测结果。
步骤5:更新马尔可夫概率转移矩阵。
马尔科夫概率转移矩阵Tij,k的变化是建立在模型进行切换的基础上的,利用运动模型在相邻时刻的概率差()对概率转移矩阵进行校正更新。
4 仿真与结果分析
采用每个轨迹点的均方根误差(RMSE)和N个轨迹点的平均均方根误差(ARMSE)对算法的预测结果进行评估。基于位置的RMSE和ARMSE的计算如下:

4.1 参数配置
在IMM 框架中,不同运动模型进行交互融合可形成不同的组合模型:CVM 与CTM 的交互结果为组合模型1,CVM 与改进的CTM 交互结果为组合模型2,CVM,CSM 与改进的CTM 交互结果为组合模型3。组合模型中包含有一个马尔科夫概率转移矩阵Ti j,k,其反映了不同运动模式下切换的趋势。
实际的船舶运动是一个连续过程,在当前时刻采用CVM 模型的条件下,下一时刻保持为CVM 模型的概率极大,而转换为其他模型的概率极小,因此,将状态转移矩阵主对角线的值设置为0.9。为体现实验的对照过程,相同维度的组合模型采用相同的概率转移矩阵。组合模型1 的状态概率转移矩阵用T1|ij,k表示;组合模型2 和组合模型3 的状态概率转移矩阵则用T2|ij,k表示如下:

对于每个运动模型,滤波器都需要设置过程协方差Q、测量协方差R以及相关误差状态协方差P的初始值P0。 在整个算法的迭代过程中,Q和R被认为是不随时间变化的参数,而P则需要在每一次迭代中更新。同时,滤波器校正步骤的步长Δt则根据AIS 数据的发送频率来设置。表1 列出了SCKF 初始参数的设置。表中:I4×4,I6×6分别为维度为4 和6 的单位矩阵; σx, σy分别为测量噪声在X,Y轴方向上的位置方差。

表1 实验初始参数设置Table 1 Setting of experimental initialization parameters
4.2 实验与分析
在实验过程中,将蒙特卡洛仿真次数设置为150 次,船舶轨迹的起始点设置为二维平面坐标系的原点 (0,0)。随着航向、航向率和航速的变化,船舶可以产生不同类型的轨迹。本文将利用不同类型的轨迹来对比分析不同运动模型的适应场景,并验证本文所提算法在船舶复杂运动场景下的性能。所采用AIS 数据的信息每10 s 更新一次。
AIS 数据存在航向信息和航速信息,不同的航向、航速变化情况对应不同的船舶运动状态。图4 展示了3 种单一运动状态的船舶轨迹,通过这些轨迹,可以验证并分析CVM,CSM 和CTM这些模型的性能及其使用场景。图中,蓝线表示船舶航行的原始轨迹,红色的点表示船舶航行过程中的测量值,这可以通过各种传感器获得。测量值与原始轨迹的值之间存在一定的偏差。k时刻的测量值对应于AIS 数据中第k个点的位置信息,其需要参与本文算法的迭代运算,对SCKF 预测过程中状态向量的预测结果进行校正,然后得到SCKF 算法的估计值 ()。原始轨迹在k时刻的值对应于式(24)中的 (),真实值不参与本文算法的迭代运算,而是在实验中结合SCKF算法的估计值 ()对算法进行性能分析。在图4(a)展示的轨迹1 中,船舶的航向发生了变化,航速保持不变,船舶进行转向匀速运动。在图4(b)展示的轨迹2 中,船舶的航向和航速均保持不变,船舶进行直线匀速运动。图4(c)所展示的轨迹3可以描述为船舶进行直线变速运动,其航向保持不变,航速发生变化。

图4 3 种单一运动状态的船舶轨迹和测量值Fig. 4 Trajectories and measurement values of ship with three single states of motion
图5 展示的是基于CVM,CSM 和CTM 模型的KF 算法对图4 中3 种轨迹跟踪结果中位置的均方根误差。观察图5(a)可以发现,对于航向变化、航速不变的船舶轨迹,基于CTM 的算法在整个跟踪过程中误差最小,基于CVM 的算法误差始终比较大,而基于CSM 的算法性能仅次于基于CTM 算法的性能。观察图5(b)可以发现,对于航向、航速均不变的船舶轨迹,基于CVM 的算法误差最小,基于CTM 的算法误差最大,基于CSM 的算法误差介于二者之间。观察图5(c)可以发现,对于航向不变、航速变化的船舶轨迹,基于CSM 的算法性能最好,基于CTM和CVM 的算法误差较大,并且误差波动的范围也较大。综合分析图5,可以得出以下结论:

图5 3 种单一运动状态下图4 跟踪轨迹的位置信息均方根误差Fig. 5 RMSEs of position data with three single states of motion in the trajectories shown in Fig. 4
1) CTM 模型对于航向变化的船舶运动的跟踪能力更强,其不适用于船舶的直线运动。
2) CVM 模型对于船舶直线运动的跟踪能力较强,最适合航向、航速均不变化的船舶运动,不适用于航向变化的船舶运动。
3) CSM 模型在对3 种轨迹跟踪过程中均有比较不错的表现,最适用于航速发生变化的船舶运动。
图4 和图5 分析了3 种单一船舶运动状态下的场景,但在实际情况下,船舶的运动状态会随着航向和航速的变化而变化。图6(a)所示为考虑船舶航向变化的场景。在航向发生变化后,船舶会由直线匀速运动变换为转向匀速运动,当航向再次保持不变时,船舶又由转向匀速运动变换为直线匀速运动。图6(b)展示的是CVM,CTM单一运动模型和组合模型1 对船舶轨迹跟踪的整个过程中位置信息的均方根误差。表2 统计了组合模型1 与单一运动模型在船舶不同运动状态下对应时间段内局部位置的平均均方根误差,其中组合模型1 是通过IMM 框架将CVM 与CTM 两种运动模型进行的交互融合。由图6 和表2 可以观察到,基于CTM 模型的算法在轨迹4 的直线段误差较大,基于CVM 模型的算法在轨迹4 的曲线段误差较大,基于组合模型1 的算法因融合了CVM 与CTM 这两种模型的优势,在不同时间段内可切换到跟踪能力较强的模型,使得能够将组合模型的误差稳定在较低范围内。因此,对于存在航向变化的船舶轨迹,适合采用组合模型1 来进行船舶轨迹跟踪。
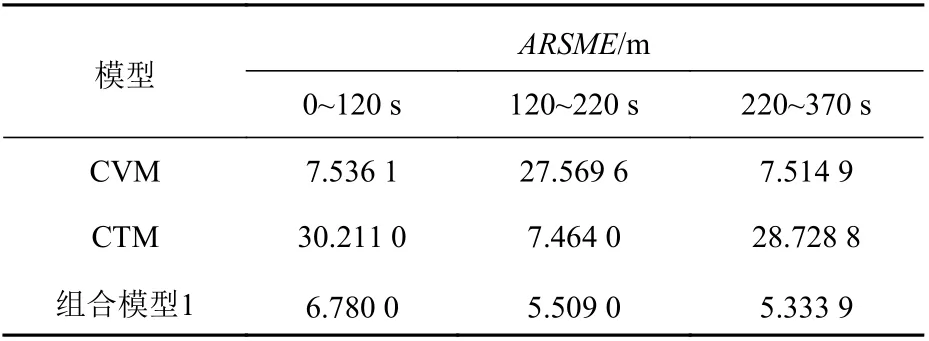
表2 组合模型1 和单一模型在不同时间段跟踪轨迹4 的位置信息平均均方根误差Table 2 ARMSEs of local position data at different time periods in Trajectory 4 using Combined Model 1 and single motion model

图6 组合模型1 和单一模型跟踪轨迹4 位置信息均方根误差Fig. 6 RSMEs of position data in Trajectory 4 using Combined Model 1 and single motion model
在船舶运动过程中,是通过操舵来改变船舶航向,不同的舵角对应的船舶转向率也不同,因此在实际的船舶运动过程中,存在具有不同转向率的转向运动场景。轨迹4 描述的是只具有一种转向率的场景,而图7(a)中的轨迹5 描述的则是船舶转向率发生变化的运动场景。CTM 模型采用的是固定的转向率,当船舶实际的转向率与CTM 模型中设置的转向率偏差较大时,其拟合效果会较差,从而影响到组合模型1 在转向运动阶段的跟踪性能。由于实验中采用的AIS 数据中缺少转向率的信息,本文将通过已知的AIS 轨迹点的航向信息来估计转向率,形成改进的CTM模型,然后再将改进的CTM 与CVM 模型进行交互融合进而形成组合模型2。
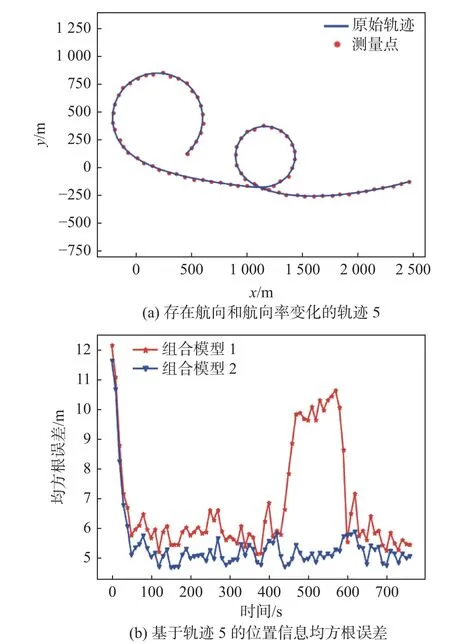
图7 组合模型1 和2 跟踪轨迹5 的位置信息均方根误差Fig. 7 RSMEs of position data in Trajectory 5 using Combined Model 1 and 2
如图7(b)所示,在2 次转向运动阶段,尤其是在第2 次转向运动阶段,基于组合模型1 的算法误差较大,出现了跟踪结果局部发散的现象。基于组合模型2 的算法在整个轨迹跟踪过程中误差均较小,且误差的波动范围也较小。表3 给出了组合模型1 和2 在轨迹5 中不同时间段的局部位置平均均方根误差。从中可以看出,在第1 次转向运动阶段,采用组合模型2 的算法其误差与采用组合模型1 算法的误差相差不大;在第2 次转向运动阶段,组合模型1 中CTM 模型设置的转向率与实际的转向率偏差较大,导致其跟踪误差出现了大幅度的变化;组合模型2 因融合了改进的CTM 模型,其跟踪误差保持在较稳定的范围内,因此对于存在航向变化及航向率变化的船舶运动,组合模型2 的适应能力较好。

表3 组合模型1 和2 在不同时间段跟踪轨迹5 的位置信息平均均方根误差Table 3 ARMSEs of position data at different time periods in Trajectory 5 using Combined Model 1 and 2
在实际的船舶运动过程中,除航向的变化外,还需要考虑航速变化的场景。图8(a)所示的轨迹6 描述的是航向变化、转向率变化以及航速变化时的船舶运动,图8(b)展示的则是轨迹6 中航速的变化情况。考虑到基于CSM 模型的算法适用于航速发生变化的船舶运动,本文将通过IMM框架实现CVM,CSM 和改进的CTM 模型进行交互融合而形成组合模型3。
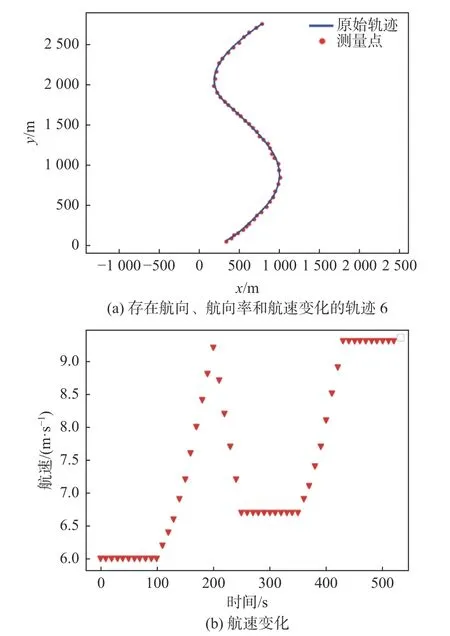
图8 轨迹6 及其航速的变化Fig. 8 Trajectory 6 and its velocity variation
图9 所示为对轨迹6 进行跟踪得到的位置信息均方根误差。一方面,采用组合模型1 分别搭配EKF 算法和SCKF 算法,并对这2 种KF 算法进行了对比分析。在整个跟踪过程中,组合模型1对轨迹6 相关船舶运动状态的描述不够准确和全面,导致采用该模型的2 种KF 算法都出现了误差明显增大的现象,这种现象被称之为局部发散。由图可以明显观察到,采用SCKF 算法时,误差变化幅度远小于EKF 算法 ,SCKF 算法对局部发散现象的抑制能力要优于EKF 算法。由表4 可知,SCKF 算法的平均均方根误差为10.975 5 m,EKF 算法的为15.693 5 m,精度提高了30.06%。总体而言,在轨迹跟踪过程中,SCKF 算法的稳定性要优于EKF 算法。
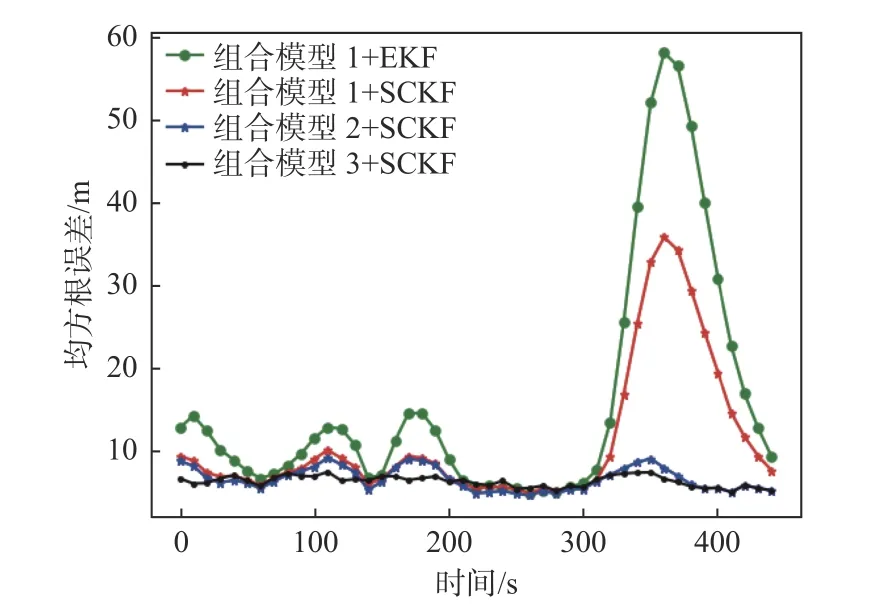
图9 3 种组合模型搭配卡尔曼算法跟踪轨迹6 的位置信息均方根误差Fig. 9 RMSEs of position data in Trajectory 6 using three combined models with Kalman filtering algorithm

表4 3 种组合模型搭配卡尔曼滤波算法跟踪轨迹6 的位置信息平均均方根误差Table 4 ARMSEs of position data in Trajectory 6 using three combined models with Kalman filtering algorithm
另一方面,分别对比分析了组合模型1,2,3搭配SCKF 算法时对轨迹6的跟踪过程中位置的均方根误差。结果显示,采用组合模型1 搭配SCKF 算法在航速发生改变的时间段存在小幅度的误差增大现象,在转向率变化的时间段误差大幅度增大,其对船舶复杂运动的适应能力较弱;采用组合模型2 搭配SCKF的算法在转向率变化的时间段拥有比基于组合模型1 的算法有更好的跟踪能力,但在航速变化的时间段仍存在小幅度的误差增大现象;采用组合模型3 搭配SCKF 的算法的误差也受到了航速变化的影响,但误差波动范围明显小于前2 种算法,整个轨迹位置的误差曲线更加平滑。
由表4 中数据可以知道,在整个轨迹跟踪过程中,采用组合模型2 搭配SCKF 算法其位置的平均均方根误差为6.709 8 m,采用组合模型3 搭配SCKF 算法的位置平均均方根误差为6.148 6 m,说明在跟踪精度上采用这2 种算法其性能相差不大,两者在性能上的差异主要体现在稳定性方面。结合图9 和表4 的实验结果可以得出结论:组合模型3 搭配SCKF 的算法对于存在航速变化的复杂船舶运动的适应能力比较强,其能将轨迹跟踪误差稳定在较小的区间范围内。
从滤波器的角度来讲,本文引入的SCKF 算法在跟踪轨迹方面其误差变化幅度比EKF 算法的小;从运动模型的角度来讲,组合模型3 搭配SCKF 算法对存在航向、航向率和航速变化的船舶运动的适应能力最强,此种算法轨迹跟踪的位置信息均方根误差变化曲线最平滑,且相比组合模型1 结合EKF 算法其平均均方根误差减小了60.80%。
前面的实验涉及了3 种组合模型,图10 和表5分别展示了这3 种组合模型搭配SCKF 算法跟踪6 类轨迹过程中的位置信息均方根误差以及平均均方根误差。其中,轨迹1,2,3属于状态变化比较单一的轨迹,轨迹4,5,6 属于状态变化比较复杂的轨迹。从中可以观察到,在所有轨迹的实验中,组合模型1 的性能是最差的,不建议采用;在轨迹1,2,3 的跟踪结果中,组合模型3 的效果明显优于组合模型2;在轨迹4,5 的跟踪结果中,组合模型3 的误差最小,与组合模型2的误差非常接近;轨迹6 涉及到航速的变化,在其跟踪结果中,组合模型3 的误差明显低于组合模型2。不过,因组合模型3 包含3 种运动模型,相比组合模型2 的2 种运动模型,需要多设置一个滤波器,故计算量更大。结合以上分析,得到结论如下:

表5 3 种组合模型搭配SCKF 算法跟踪6 条轨迹的位置信息平均均方根误差Table 5 ARMSEs of position data in the six trajectories using three combined models with SCKF algorithm
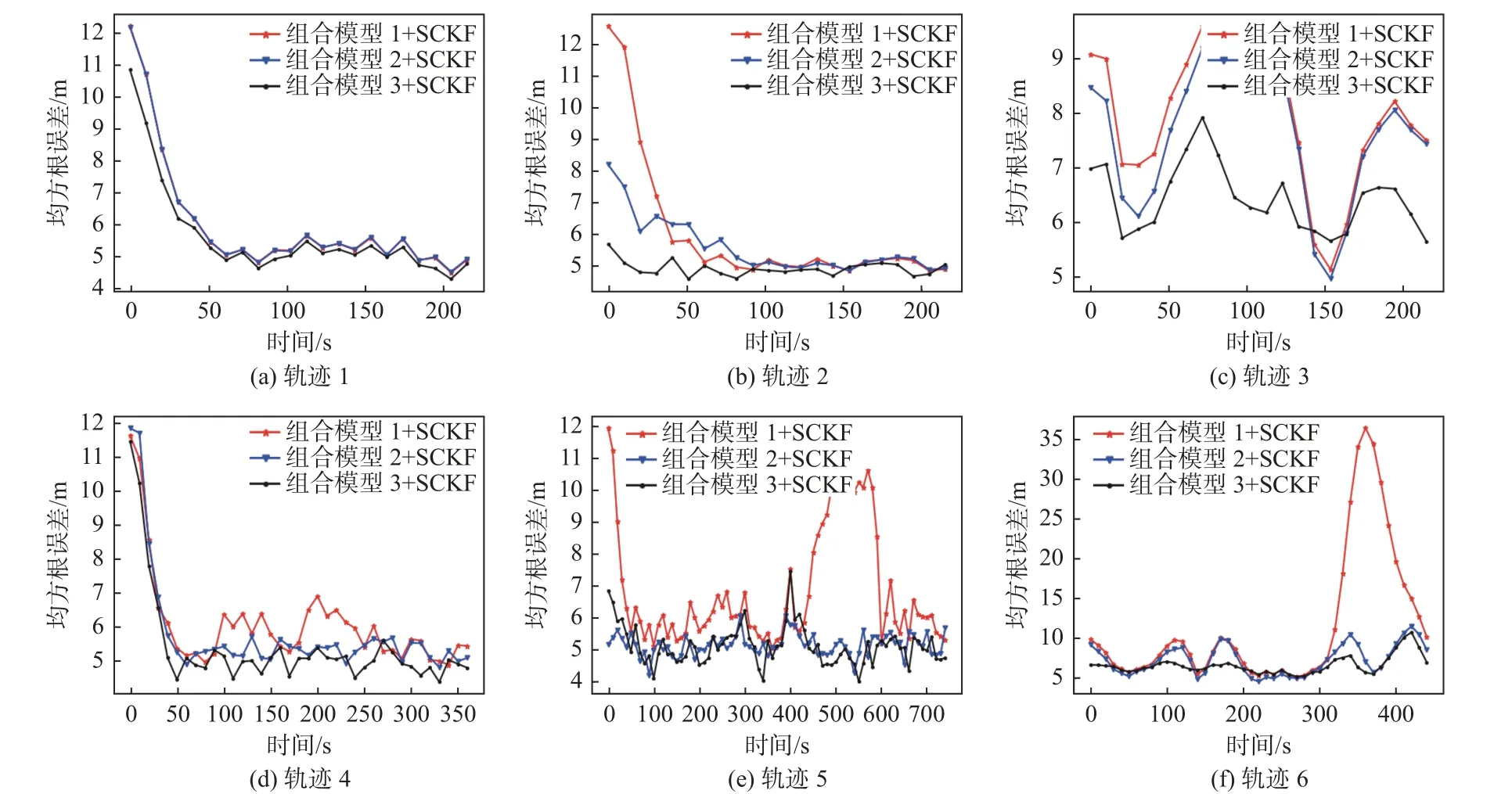
图10 3 种组合模型搭配SCKF 算法跟踪6 条轨迹的位置信息均方根误差Fig. 10 RMSEs of position data in the six trajectories using three combined models with SCKF algorithm
1) 在所有场景下,组合模型3 的性能都是最好的,但计算量也是最大的;
2) 对于状态变化比较简单的轨迹,建议采用组合模型3;
3) 对于状态变化比较复杂的轨迹,如果不存在航速的变化,在缺乏计算资源的情况下,建议采用组合模型2,其他情况下采用组合模型3 效果更好。
图11 所示为在船舶轨迹6 的轨迹跟踪实验中,组合模型2 和3 的基础模型的概率随船舶运动变化的时序图。图中,各条曲线分别显示了其对应基础运动模型滤波后的模型概率,代表了当前时间步长模型的依赖程度。曲线的概率越高,所对应的模型越有可能在当前时间步长用于轨迹跟踪。轨迹6 包含有直线运动、转向运动和变速运动,在图11 中,组合模型2 的概率曲线的变化情况比较混乱,无法准确识别轨迹6 运动状态的变化;相比而言,组合模型3 的概率曲线的变化更具规律性,能够描述出轨迹6 运动状态的变化。然而,模型的切换存在较小的滞后,这是因为滤波器不是依靠精确的船舶运动模型进行迭代计算,而是通过迭代计算测量值与估计值间的差值,逐渐切换到该差值最小时所对应的运动模型,从而完成模型的过渡。这种转换过程需要一些时间,因为测量值与估计值间的差值不会显著或是立即改变。
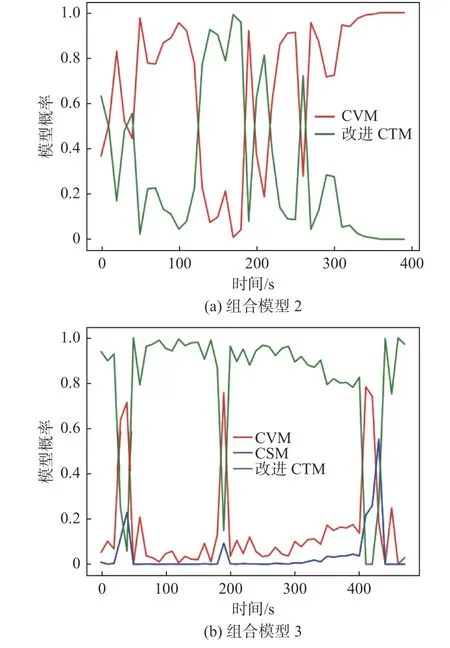
图11 组合模型2 和3 在轨迹6 中的模型概率时序图Fig. 11 Time-series of model probabilities for Combined Model 2 and 3 in Trajectory 6
5 结 语
AIS 是海上交通普遍使用的一种系统,针对AIS 数据中存在虚假信息以及不连续性的问题,本文提出了一种IMM-SCKF 算法来对船舶轨迹进行跟踪。通过引入SCKF 算法代替EKF 算法来执行对AIS 数据的轨迹跟踪,避免了EKF 算法容易出现局部发散的现象,提高了滤波器的数值稳定性。采用IMM 框架将多个模型进行融合并进行自适应转换,表征了船舶在不同时刻的运动状态。首先,对参与模型融合的CTM 运动模型进行改进,用已知AIS 轨迹点的航向信息来估计转向率,并替代CTM 的固定转向率,使得组合后的模型能够更好地表征船舶航向的变化。随后,通过对比实验,验证了基于CVM,CSM 和改进CTM 的组合模型在各种类型船舶轨迹的跟踪实验中都具有最小的误差和误差波动幅度,适合大多数情况下的船舶轨迹跟踪。然而,基于CVM,CSM 和改进CTM 的组合模型计算量比较大,当计算资源紧张且船舶存在航向和航向率变化特征时,可以考虑采用CVM 和改进CTM 的组合模型进行轨迹跟踪。
总体而言,本文提出的IMM-SCKF 算法能对船舶在不同时刻的运动状态进行较为全面和准确的描述,其在实际的轨迹跟踪过程中,在跟踪精度和稳定性两个方面均有着比较理想的效果,能有效提高AIS 的服务质量,为船舶轨迹的预测和船舶导航提供有力的支撑。然而在实验过程中,IMM 框架下模型的实际切换过程相比理想的切换过程存在一定的滞后,这在一定程度上影响了IMM-SCKF 算法在运动状态变换时轨迹跟踪的精度。
