自主水下航行器自适应S 面三维轨迹跟踪的仿真验证
2022-09-06李文魁周铸宦爱奇夏宇轩
李文魁,周铸*,2,宦爱奇,夏宇轩
1 海军工程大学 电气工程学院,湖北 武汉 430033
2 中国人民解放军 92768 部队,广东 汕头 515000
3 中国人民解放军 91206 部队,山东 青岛 266000
4 海军工程大学 教务处,湖北 武汉 430033
0 引 言
自主水下航行器(AUV)因体积小、成本低、能够完成多样化任务等特点,成为了海洋探索和海底作业的重要载体,而良好的航迹跟踪性能是AUV 进行海底作业的重要保证。目前,航迹跟踪方式主要包括路径跟随和轨迹跟踪。前者只需考虑在空间维度上沿预定路径航行,后者则需在预定时间到达预定位置,同时满足空间和时间维度上的跟踪要求。Breivik 等[1]通过引入导引角的概念定义新的导引律,使导引律不受AUV 动力学的改变而改变,从而提高了通用性。陈东等[2]在文献[1]的基础上,利用反歩法,设计了一种基于AUV模型的非线性控制器,较好地实现了轨迹跟踪,但控制算法对模型参数准确度要求较高。孙巧梅等[3]基于反演法和变结构模糊控制律设计了一种AUV 航迹跟踪控制律,能较好地抑制外界干扰,实现了轨迹平稳跟踪,但算法的模糊控制规则设置较为困难。刘学敏等[4]借鉴PID 控制器的结构,使用Sigmoid 函数设计了一种S 面控制器,其结构简单且具有类似于模糊控制的智能性,但控制参数整定较为困难。Sahu 等[5]设计了一种静态输出反馈控制器,用于控制水下机器人沿着期望的轨迹运动。Oh 等[6]使用视线(line-of-sight, LOS)导引法进行导引,针对欠驱动的AUV,设计了一种状态空间形式的模型预测控制器,获得了比PID 控制算法更优的效果。刘丽萍等[7]通过在控制器中加入自适应律,设计了一种自适应反演滑模轨迹跟踪控制器,该控制器能够较好地处理水动力参数不确定和海流干扰的问题,但设计的海流观测器在工程上较难实现。
为满足AUV 在空间和时间维度上的跟踪需求,本文将AUV 的轨迹跟踪问题简化为与时间相关的参数化轨迹参考点的方式;然后,使用文献[1]中的LOS 导引律,将AUV 对参考点的跟踪转化为对指令航向、指令纵倾和指令速度的跟踪,并改进传统的LOS 导引律,设计三维轨迹变前视距离的LOS 导引律; 其后,在实现对航向、纵倾和速度的控制后,基于文献[4],设计具有控制参数自调整能力的自适应S 面控制器,以减小控制参数整定难度和增强抗干扰能力; 最后,通过数值仿真验证所提算法的有效性。
1 AUV 空间运动模型
图1 所示为AUV 运动的惯性坐标系(I 坐标系)和载体坐标系(B 坐标系)。I 坐标系取地球切平面坐标系,原点取地球椭球体表面某固定点,坐标轴定义为北东地(NED)。B 坐标系原点取为AUV 重心,坐标轴指向的定义为前-右 -下。
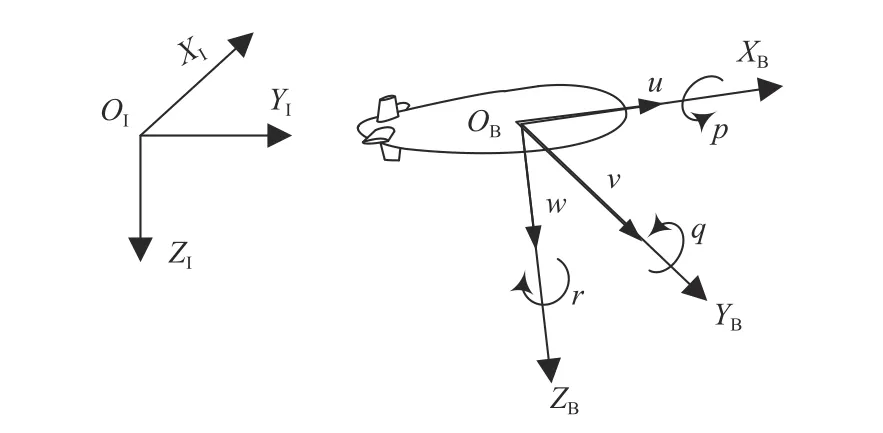
图1 AUV 运动的惯性坐标系和载体坐标系Fig. 1 Inertial frame and body frame of AUV motion
令AUV 位置姿态矢量 ηI=[pI,Θ]T(其中,位置pI=[x,y,z]T,姿 态 Θ=[φ,θ,ψ]T,x,y,z分 别 为 纵 向、横向和垂向位移, φ,θ,ψ分别为横倾角、纵倾角和航向角,上标I表示I坐标系)、速度矢量νB=[vB,ω]T(其中,线速度vB=[u,v,w]T,u为纵向速度,v为横向速度,w为垂向速度,上标B表示B 坐标系)、角速度ω=[p,q,r]T(其中,p为横倾角速度,q为纵倾角速度,r为转艏角速度),建立式(1)和式(2)所示AUV 六自由度空间运动模型[8]。
运动学方程:
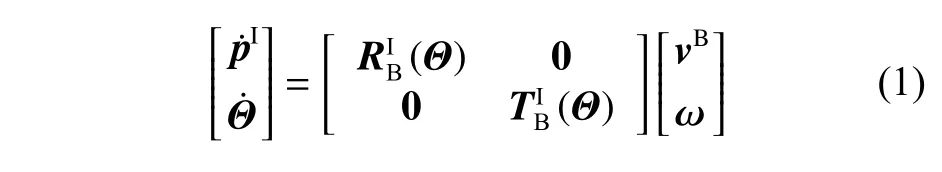
动力学方程:
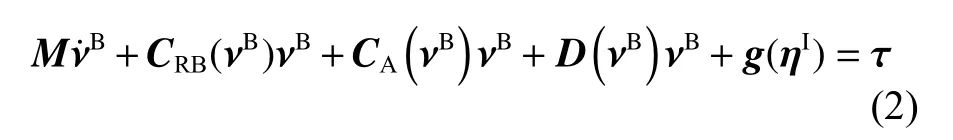
AUV 在水下航行时会受到海流干扰,因此,假设AUV 仅受到常值海流干扰且 I坐标系下的海流速度为
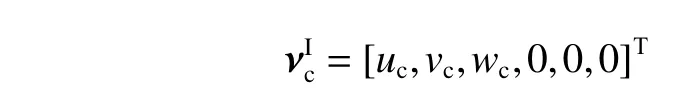
B 坐标系下的海流速度为

B 坐标系下的AUV 相对速度为
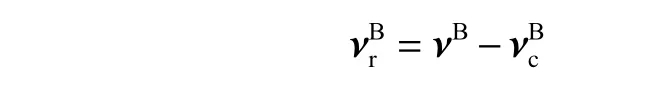
则在有海流干扰的情况下AUV 动力学方程为

2 AUV 三维导引律
2.1 从I 系到参考轨迹系(P 系)的坐标转换


建立参考轨迹坐标系(P 坐标系),其原点为P,XP轴 沿参考轨迹的切线方向, χP和 γP为轨迹方位角和轨迹升角,分别表示为:
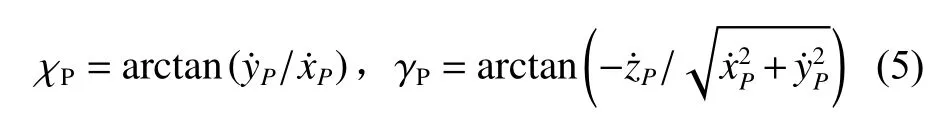
将I 坐 标 系 绕ZI轴 旋 转 角 χP,旋 转 矩 阵 为RZI(χP), 再绕YI轴 旋转角 γP, 旋转矩阵为RYI(γP),得到参考轨迹坐标系,对应的旋转矩阵为
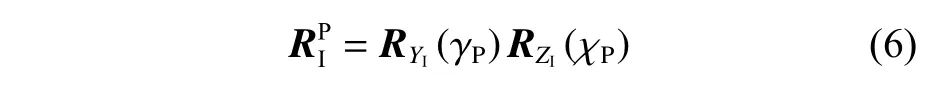
式中:
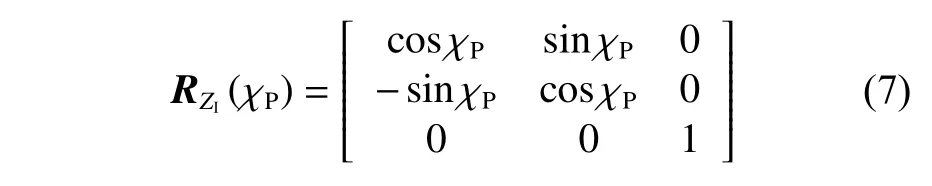

其中:
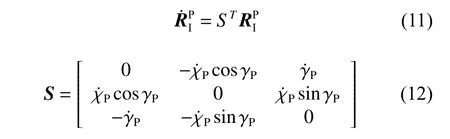
式中,S为反对称矩阵,ST=-S。 设vP为P点在参考轨迹坐标系下表示的速度矢量vP=[UP,0,0]T,则有
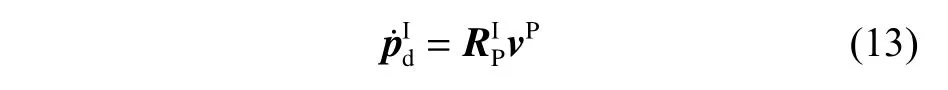
2.2 从P 系到视线速度坐标(L 系)的坐标转换
如图2 所示,PL为视线速度坐标(L 坐标系)导引的前视点,视线速度UL由AUV 实时位置点B指向PL。 在B点处,将P 坐标系绕ZP轴旋转方位导引角 χL,旋转矩阵为RZP(χL), 再绕YP轴旋转俯仰导引角 γL, 旋转矩阵为RYP(γL),得到视线速度坐标系,其原点与AUV 固联,其XL轴 沿UL方向,P 坐标系到L 坐标系旋转的坐标转换矩阵为

图2 轨迹跟踪示意图Fig. 2 Trajectory tracking diagram

2.3 轨迹导引律
旋转方位导引角 χL和俯仰导引角 γL可由如下LOS 法[9]得到。
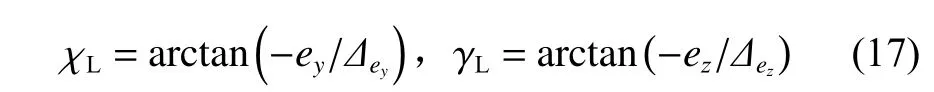
式中,前 视 距 离 Δey和 Δez分 别 用 于 将AUV 导 引 到P 坐标系的X-Z平面和X-Y平面。在实际导引过程中,希望能够在轨迹偏差较大时,AUV 可以迅速靠近期望的轨迹,此时前视距离需要得较小;在轨迹偏差变得较小时,AUV 能缓慢平滑地接近期望的轨迹,此时前视距离需要得较大。基于此标准,设计如式(18)所示的变前视距离。

基于轨迹跟踪误差 εp,设计如式(20)所示的李雅普诺夫稳定函数。
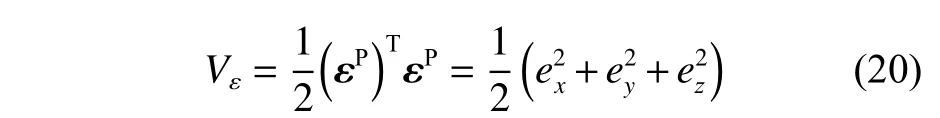
对式(20)进行时间求导,因 (εP)TSTεP=0,故可得
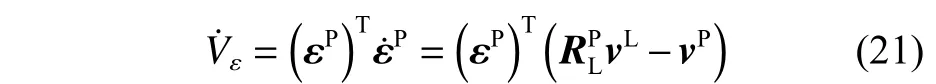
展开式(21),可得

基于李雅普诺夫稳定性判据,令
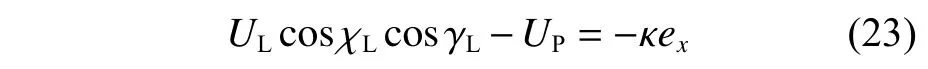
式中, κ为比例系数。
将式(18)和式(23) 代入式(22),可得到导引算法的李雅普诺夫稳定性判据如下:
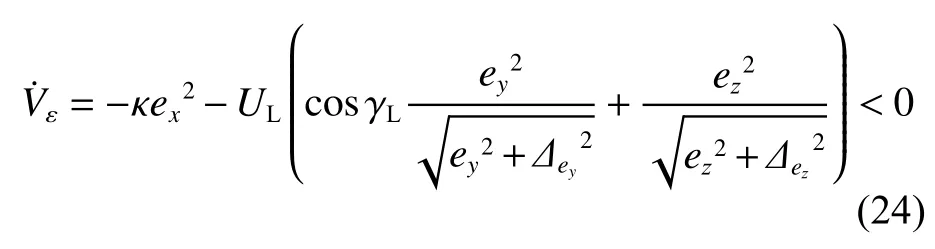
由式(23) 可得

并且,得到期望的纵向速度为
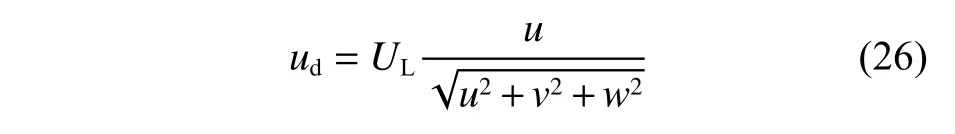
此外,由式(17)可得 -π/2 <χL<π/2,-π/2 <γL<π/2 ,故 c osχLcosγL≠0,则式(25)为非奇异。
将I 坐标系绕ZI轴 旋转期望的迹向角 χd,旋转矩阵为RZI(χd) ,再绕YI轴 旋转期望的潜浮角 γd,则旋转矩阵为RYI(γd),并得到L 系坐标。从I 坐标系到L 坐标系的旋转矩阵表示为

联立式(16)和式(27),得到期望的迹向角χd和期望的潜浮角 γd分别如式(28)所示。

考虑到式(28)的奇异性问题,在实际计算中,可使用函数atan2 替代函数arctan 来解决式(28)的奇异值问题。另外,由于AUV 航行中会产生漂角和攻角,期望的航向角 ψd和期望的纵倾角θd可由下式计算。
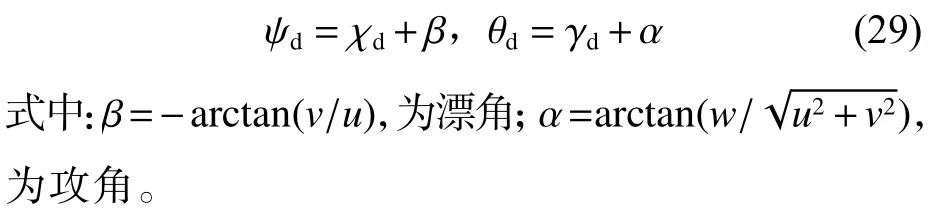
3 控制器设计
S 面控制器将模糊思想与PID 控制相结合,是一种结构简单、鲁棒性能好的非线性控制器[10]。
将运动参数误差量及其变化率归一化,可得


式 中,kpi,kdi(i=u,θ,ψ)为 控 制 器 参 数(下 标 p 和d 分别表示PID 控制器中的比例和微分),则控制器输出的驱动力为
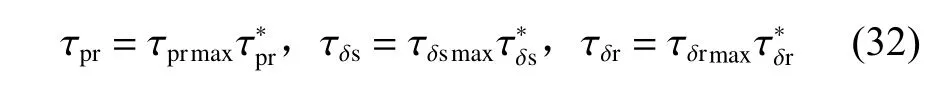
这里,以 τpr为 例,设计自适应学习算法对kpi,kdi进行调节,使用梯度下降法[11]修正控制器参数,设计代价函数G为
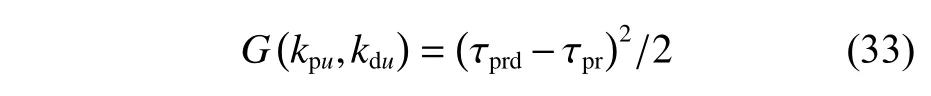
式中, τprd为 期望的输出推力,由ud经AUV 模型推算获得。
对式(33) 中的kpu,kdu进行泰勒展开,忽略高阶项,并记为
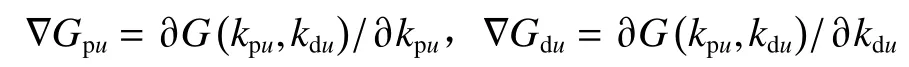
则有

为保证 Δkpu∇Gpu<0, Δkdu∇Gdu<0,取

式中: λpu和 λdu为学习率, 0 <λpu<1,0 <λdu<1,则有
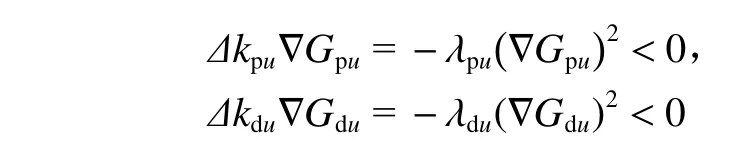
代价函数G可迭代收敛至0。联立式(31)、式(33)和式(35),可得

故m+1 时刻的控制器参数可按下式递推得到。
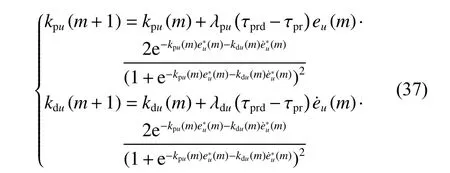
此外,对 τδs, τδr的 控制参数kpθ,kdθ,kpψ,kdψ也分别按此法进行修正。
4 仿真验证
本节以REMUS 100 AUV[12]为例,在Matlab 软件中分别对控制算法和导引律进行仿真验证。AUV 的初始状态(含位置、姿态、速度及角速度)为:
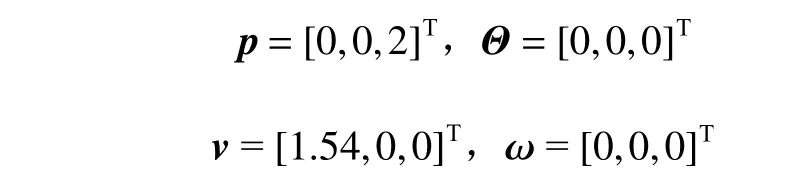
4.1 控制算法的验证
分别对控制器控制进行仿真,将PID 控制和传统的S 面控制方法与采用自适应S 面控制方法的结果进行对比。设置指令的航向角 ψ 、纵倾角θ和 纵 向 速 度u分 别 为 ψc=45°, θc=5°,uc=2 m/s,在50 s 时刻加入海流干扰,海流速度为

1) 由试凑法得到如下较理想的控制参数。
S 面控制器控制参数:
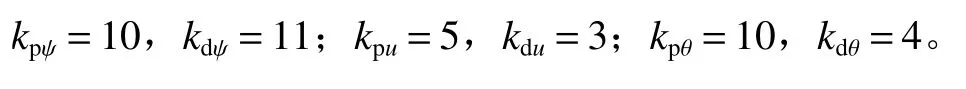
PID 控制器控制参数:
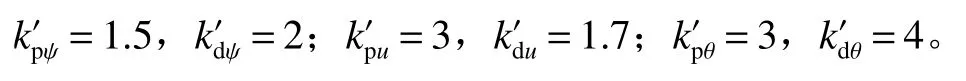
令自适应S 面控制器控制参数与传统S 面控制器的相同。经仿真,可得在较理想的初始控制参数情况下(工况1)的航向角 ψ、纵向速度u和纵倾角 θ对比图及自适应S 面控制器控制参数变化图(图3~图8)。
由图3 可见,在未加入干扰及较为理想的初始控制参数下,因PID 控制和传统的S 面控制方法航向控制效果已较理想,自适应S 面控制对航向控制效果无明显提升; 在50 s 时刻加入海流干扰后,相比PID 控制器和传统的S 面控制器,自适应S 面控制器更早地调整到了期望值,且振荡次数更少。图4 反映了此时其在航向控制过程中控制参数的变化。

图3 较理想初始控制参数下航向控制对比(工况 1)Fig. 3 Comparison of yaw control under desirable initial parameters (Case 1)
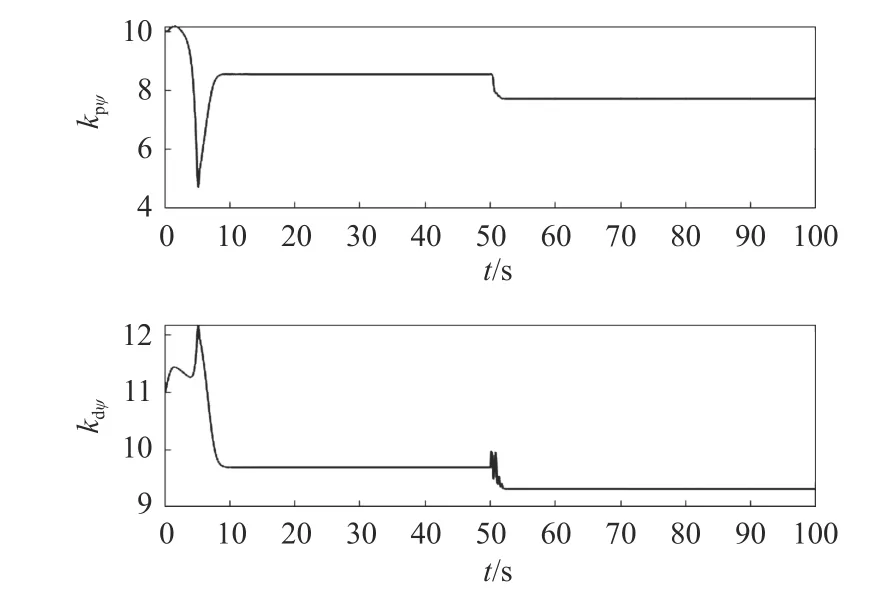
图4 航向自适应S 面控制器参数变化(工况1)Fig. 4 Variation of yaw for adaptive S-plane controller (Case 1)
由图5 可见,自适应S 面控制对速度控制效果没有明显提升;在50 s 时刻加入海流干扰后,相比PID 控制器和S 面控制器,自适应S 面控制器更早调整到了期望值,且振荡次数更少。图6 反映了此时其在纵向速度控制过程中控制参数的变化。

图5 纵向速度控制对比(工况1)Fig. 5 Longitudinal velocity control contrast (Case 1)
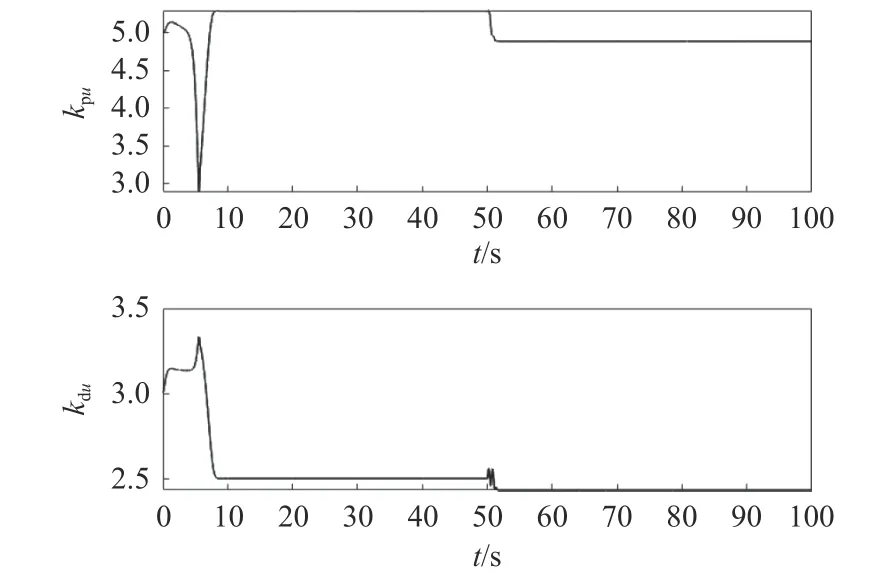
图6 纵向速度自适应S 面控制器参数变化(工况1)Fig. 6 Variation of longitudinal velocity for adaptive S-plane controller (Case 1)
由图7 可见,相比PID 控制,传统的S 面控制和自适应S 面控制均能更快地跟踪上指令的纵倾角,在50 s 时刻加入海流干扰后,相比PID 控制器和传统的S 面控制,自适应S 面控制能更早地调整到期望值,且振荡次数更少。图8 反映了此时其在纵倾控制过程中控制参数的变化。
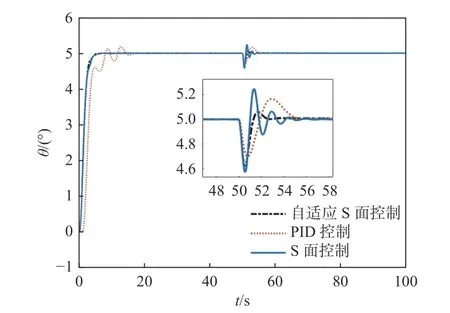
图7 纵倾控制对比(工况1)Fig. 7 Trim control contrast (Case 1)

图8 纵倾自适应S 面控制器参数变化(工况1)Fig. 8 Variation of trim for adaptive S-plane controller (Case 1)
综上,自适应S 面控制器相比PID 控制器和传统S 面控制器对海流干扰具有更强的鲁棒性。
2) 改变控制参数,令传统的S 面控制器和自适应S 面控制器控制参数均为
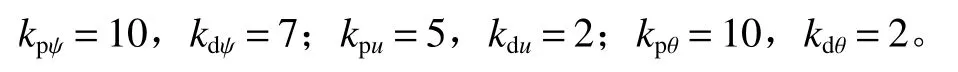
PID 控制器控制参数为

经仿真,可得到在初始控制参数发生变化(不理想)的情况(工况2)下航向角 ψ、纵向速度u和纵倾角 θ对比图以及自适应S 面控制器控制参数变化图(图9~图14)。
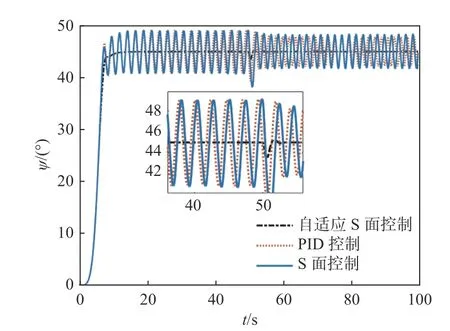
图9 初始控制参数变化下航向控制对比(工况2)Fig. 9 Comparison of yaw control under undesirable initial parameters (Case 2)
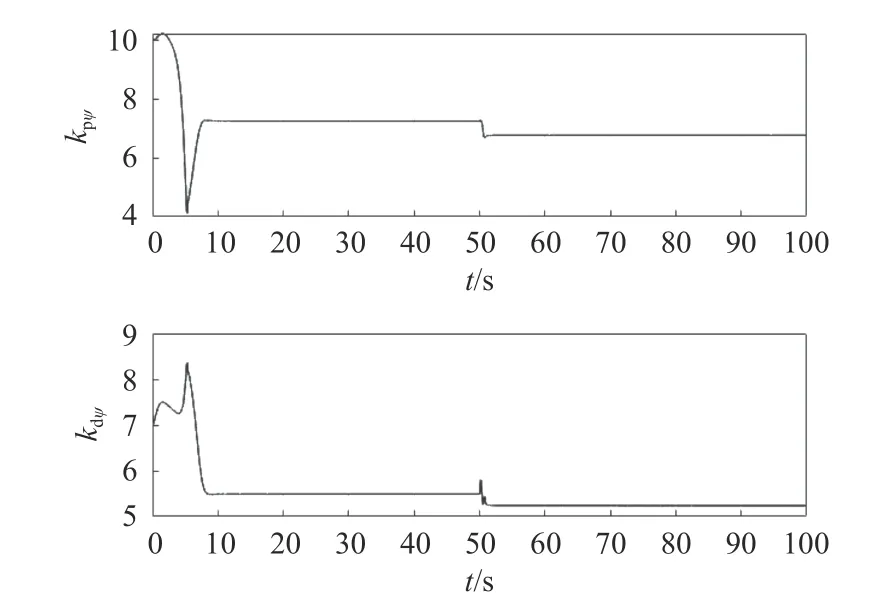
图10 航向自适应S 面控制器参数变化(工况2)Fig. 10 Variation of yaw for adaptive S-plane controller (Case 2)
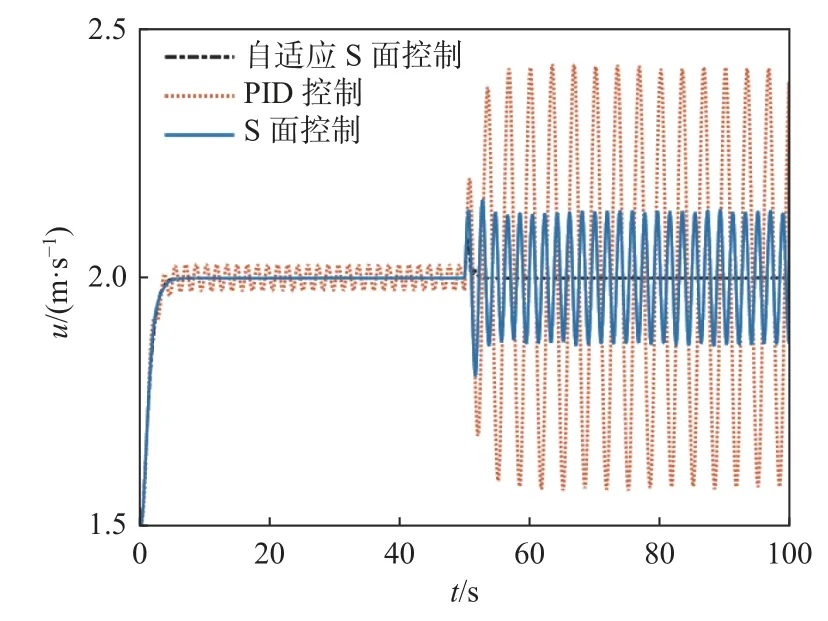
图11 纵向速度控制对比(工况2)Fig. 11 Longitudinal velocity control contrast (Case 2)
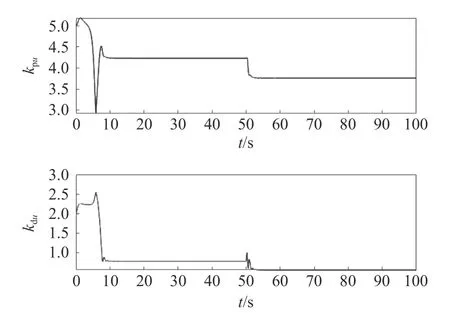
图12 纵向速度自适应S 面控制参数变化(工况2)Fig. 12 Variation of longitudinal velocity for adaptive S-plane controller (Case 2)

图13 纵倾控制对比(工况2)Fig. 13 Trim control contrast (Case 2)
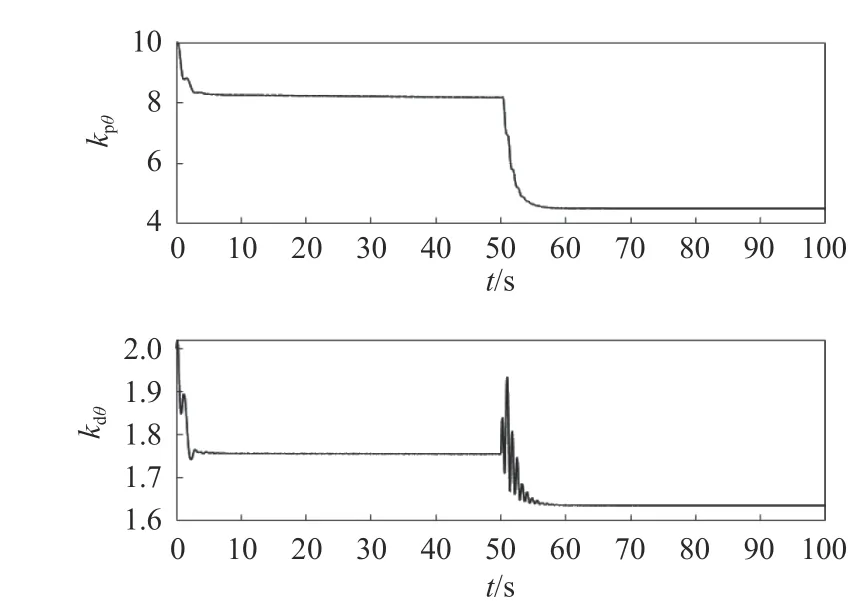
图14 纵倾自适应S 面控制器参数变化(工况2)Fig. 14 Variation of trim for adaptive S-plane controller (Case 2)
由图9 和图10 可见,在改变控制参数后,PID 控制器和传统的S 面控制器无法稳定AUV的航向,且始终在45。上下振荡,而自适应S 面控制下的AUV 其控制参数会自适应调节,最终使AUV航向能稳定在45。。
图11~图14 也具有如图9 和图10 相同的现象。可见,在控制参数产生较大变化的情况下,PID 控制和传统的S 面控制方法已经无法实现对AUV 的稳定控制,但自适应S 面控制方法则能够通过改变控制参数的大小来实现对AUV 的航向角、纵向速度、纵倾角的控制。对于自适应S 面控制而言,在控制参数整定时,不需要反复试凑来寻找最佳参数,而只需找到一定范围内的参数,即可实现对AUV 的控制,并减小了参数整定的难度。
4.2 导引律的验证
在采用自适应S 面控制控制方法的基础上,为验证变前视距离LOS 法的优点,增加LOS[9]导引方法与之对比。为此,在150 s 时刻加入海流干扰,海流速度=[0.5,0.2,0,0,0,0]T,分别进行直线和曲线轨迹跟踪仿真。
直线参考轨迹为
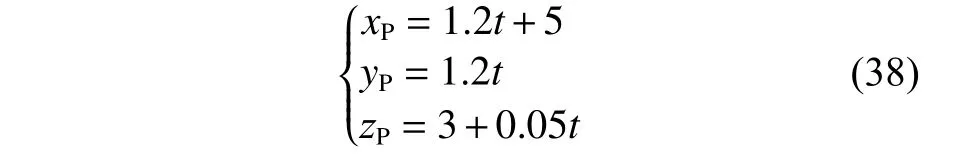
式中,t表示时间,s。
通过直线轨迹跟踪仿真,得到上述两种导引方法下的轨迹对比图(图15)和轨迹跟踪误差对比图(图16),以及变前视距离LOS 法下的航向角ψ、纵倾角 θ 和纵向速度u跟踪图(图17~图19)。

图15 不同导引法下直线轨迹跟踪对比Fig. 15 Comparison of straight line trajectory tracking under different guidance laws
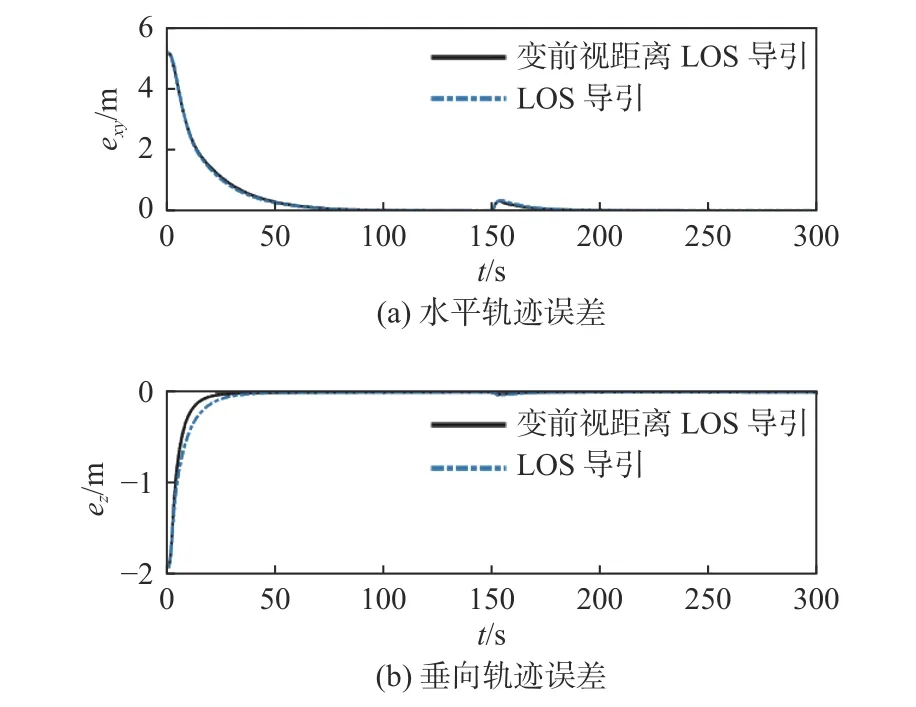
图16 直线轨迹跟踪误差Fig. 16 Erros of straight line trajectory tracking

图17 直线轨迹跟踪的航向Fig. 17 Yaw of straight line trajectory tracking

图18 直线轨迹跟踪的纵倾Fig. 18 Trim of straight line trajectory tracking
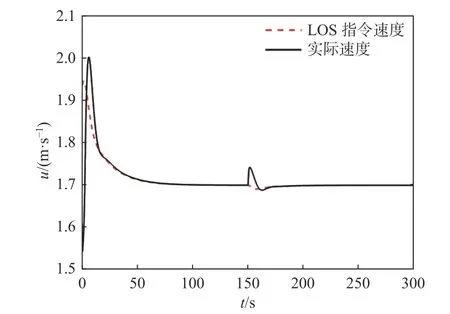
图19 直线轨迹跟踪的纵向速度Fig. 19 Longitudinal velocity of straight line trajectory tracking
由图15 和图16 可见,在直线轨迹跟踪情况下,变前视距离和固定前视距离LOS 两种导引法均能使AUV 跟踪上参考轨迹,但变前视距离LOS 法的轨迹跟踪误差能更快收敛到0 附近,其跟踪速度更快;在150 s 时刻加入海流干扰后,水平和垂直轨迹误差均能在一定时间内收敛到0 附近,AUV 在偏离预定轨道后能快速回到参考轨迹,说明导引律具有一定的鲁棒性。
结合图15~图19 可见,在AUV 偏离参考轨迹时,变前视距离LOS 导引法会不断调整指令的航向角 ψ、纵倾角 θ 和 纵向速度u,以使AUV 跟踪上参考轨迹。而且,轨迹跟踪误差越大,指令的航向角、纵倾角和纵向速度的变化越大,且实际的航向角、纵倾角和纵向速度经短暂调整后可跟踪上指令信号。
曲线参考轨迹为
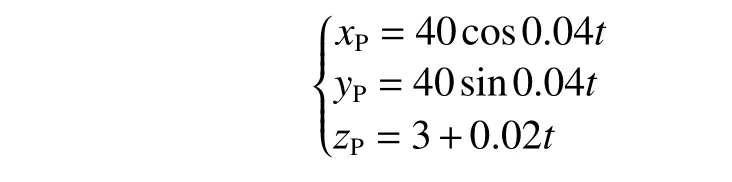
通过曲线轨迹跟踪仿真,得到两种导引方法下的轨迹对比图(图20)和轨迹跟踪误差对比图(图21) 及变前视距离LOS 导引法下的航向角、纵倾角和纵向速度跟踪图(图22~图24)。
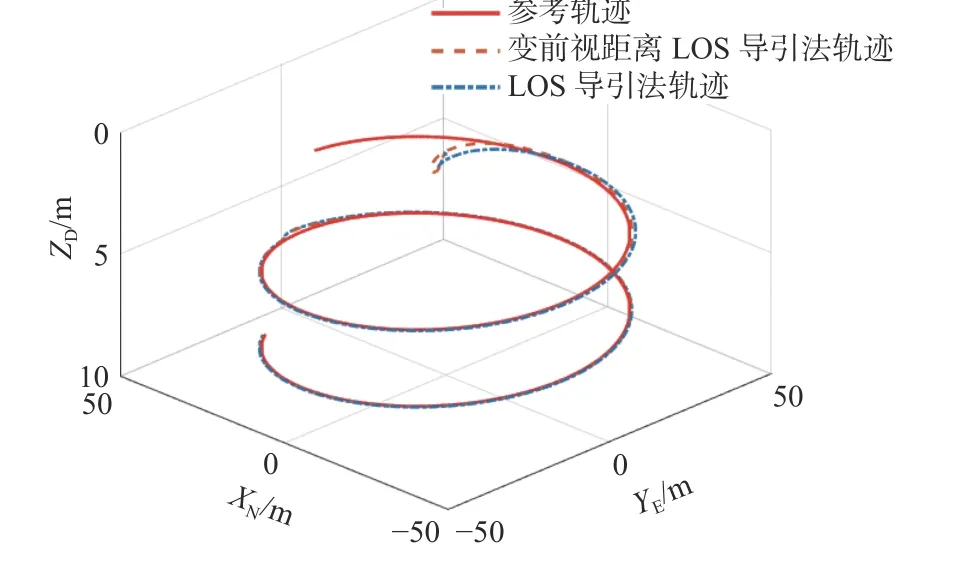
图20 不同导引方法下曲线轨迹跟踪对比Fig. 20 Comprison of curve trajectory tracking under differentguidance laws

图21 曲线轨迹跟踪误差Fig. 21 Errors of curve trajectory tracking
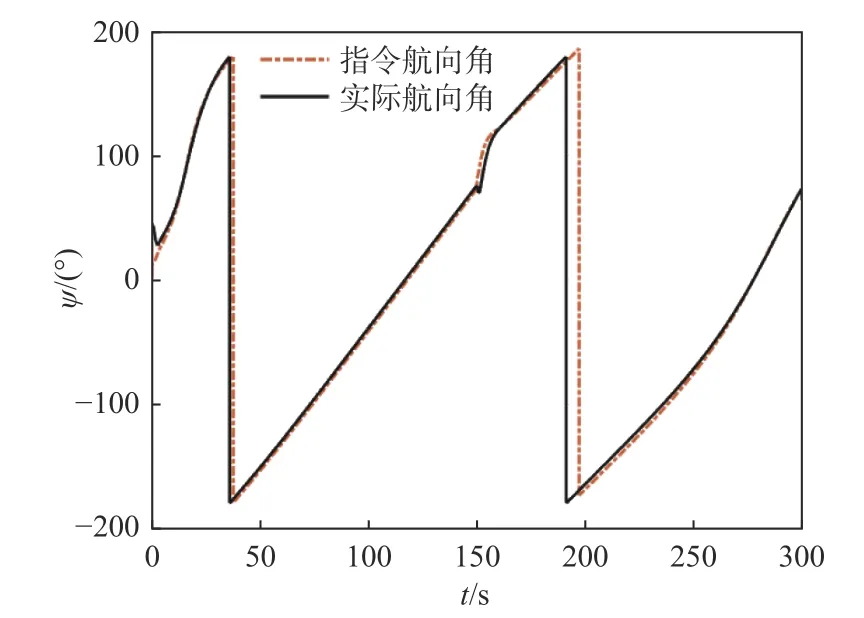
图22 曲线轨迹跟踪的航向Fig. 22 Yaw of curve trajectory tracking
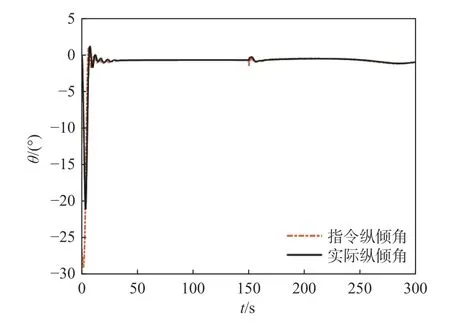
图23 曲线轨迹跟踪的纵倾Fig. 23 Trim of curve trajectory tracking
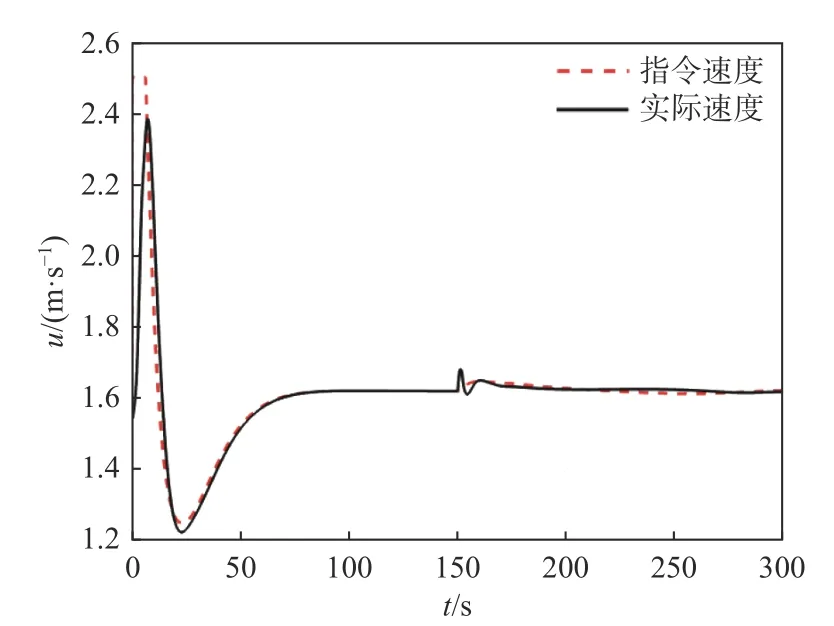
图24 曲线轨迹跟踪的纵向速度Fig. 24 Longitudinal velocity of curve trajectory tracking
结合图20~图24 可见,在曲线轨迹跟踪情况下能够得出与直线轨迹跟踪相同的结论。由此可知,变前视距离LOS 导引法下的AUV 具有一定的空间轨迹跟踪能力,对海流干扰有一定的鲁棒性,跟踪收敛速度也比传统LOS 导引法更快。
5 结 语
本文通过分析AUV 的运动学和动力学特性,构建了六自由度AUV 轨迹跟踪数学模型,采用设计的三维轨迹变前视距离LOS 导引律和自适应S 面控制器控制。以REMUS 100 AUV 为对象进行仿真分析,验证了所设计的导引律的有效性。结果证明,本文所设计的轨迹跟踪控制算法具备较好的直线和曲线轨迹跟踪特性,对海流干扰也具有一定的鲁棒性,且设计的自适应S 面控制器能够降低控制参数整定的难度,增强AUV的抗干扰能力。
然而,本文设计的控制算法仅考虑了常值海流干扰下的AUV 的轨迹跟踪问题,未来的研究工作将考虑变海流干扰因素,并采用更加智能的控制算法。
