基于SWASH模型的珊瑚岛礁波生环流模拟研究
2022-09-05陈松贵王建平
陈松贵,王建平,高 骏,谭 召
(1.交通运输部天津水运工程科学研究所,天津 300456;2.91053部队,北京 100070;3.中船第九设计研究院工程有限公司,上海 200063;4.中交四航局港湾工程设计院有限公司,广州 510220)
珊瑚礁是深海和浅海中均存在的一种珊瑚虫骨骼沉积形成的岩体,我国广阔的海域如东沙、西沙、中沙、南沙诸群岛和台湾岛等区域拥有丰富的珊瑚礁资源。近年来,我国开展了一系列珊瑚岛礁成陆工程,建设了诸如港口、机场、码头、灯塔、通信等相关设施,这些工程与设施在复杂的岛礁海岸水动力环境下的稳定性问题越来越受到学者们的关注[1]。不同于以往常见的近岸缓变地形的水动力环境,岛礁附近水深剧烈变化且存在潟湖和裂口等。当远海波浪传播到珊瑚礁时,由于礁前斜坡较陡、水深急剧变化,波浪在此发生强烈破碎,破碎波在礁坪上传播消耗大量能量后继续形成向前传播的波浪,并且破碎波会在礁坪上产生部分波生流以回流的形式返回到外海[2]。
在这类环境下,研究波浪在珊瑚礁地形的传播变形与增水等水动力特征,对工程建设与珊瑚礁保护具有重要意义。珊瑚礁地形上波浪传播的研究方法涉及理论分析、现场观察、物理模型实验与数值模拟等。Gourlay[3]通过一系列水槽物理模型实验研究了规则波作用下礁坪上的波生流问题,并给出了波生流经验计算关系式。Demirbile等[4]为了研究礁坪增水及岸滩波浪爬高随不规则波及风的关系,开展了风浪水槽实验研究,结果表明波浪爬高会因珊瑚礁而出现衰减。梅弢等[5]研究了50 a一遇和常年平均波高在概化珊瑚礁地形上的传播过程,总结了礁坪位置外海波浪的传播规律。Yao等[6]基于物理模型实验研究了礁前斜坡坡度、礁坪水深与破碎波特征(破碎带宽度、破波位置与破碎类型)之间的关系。柳淑学等[7]基于物理模型实验研究了波浪破碎位置同波高变化的关系。姚宇等[8]在水槽实验中证实了波浪增水、破碎受冠顶水深影响的现象。陈松贵、王建平等[9-12]对建有防浪堤的珊瑚礁陡变地形上波浪的传播变形、越浪规律和波浪力特征进行了一系列研究,并总结了礁坪波浪增水出现的原因,即在礁缘处波浪破碎引起辐射应力的急剧变化。Lowe等[13]讨论了夏威夷Kaneohe湾珊瑚礁不同入射波况对波浪破碎和环流的影响,提出了一个理想的礁坪-潟湖-裂口环流模型。Yao等[14]在波浪水槽布置了带裂口的珊瑚礁物理模型,模拟礁坪增水和波生流在裂口存在时的变化情况。近年来基于Navier-Stokes方程的非静压模型得到快速发展(SWASH、NHWAVE等)。此类模型省去传统CFD模型模拟自由水面时采用的如VOF、level set等过程,直接假定自由水面是关于水平位置的单值函数[15]。Buckley等[16]分别应用了XBeach模型、SWAN模形、SWASH模型模拟波浪在陡坡岸礁的传播变形,结果表明在模拟礁坪上的波生流时非静压模型可以得到更为准确的结果。姚宇等[17]通过对珊瑚岛礁附近的孤立波的传播变形特征进行的数值模拟,证实了非静压模型NHWAVE相比于Boussinesq模型对垂向流速分布特征有着更高的模拟精度。邹国良等[18]在SWASH模型中引入了涡粘模型以提高其模拟波浪破碎的能力,且使模型在较少的垂向分层下即可得到较好的结果。Zheng、Yao[19-20]等采用三维港池物理模型研究了礁坪-潟湖-裂口的环流特征和波浪分布。
本文采用SWASH模型,模拟了珊瑚岛礁的三维港池实验,并与物理模型试验的波高和流速结果进行对比,验证模型的准确性。最后给出了不同外海波浪条件下珊瑚岛礁地形上波高、流速、增水和波生流的变化规律。
1 SWASH模型简介
1.1 控制方程
SWASH(Simulating Waves till Shore)模型由荷兰代尔夫特理工大学的Stelling、Zijlema和Smit等学者历时近15 a开发完成[18-20]。模型考虑了波浪运动中的非静压影响,适用于深海至浅水条件下的波浪和水流运动的模拟,特别是对于复杂地形如三维区域下的波浪破碎所引起的增水和波生流有较好的适用性。SWASH的控制方程包括浅水方程、垂向动量方程和水平动量方程中附加的非静压项,在求解时把控制方程分解为静压项和非静压项两部分分部求解[21]。其控制方程如下
(1)
(2)
(3)
(4)
式中:t为时间;x、y和z方向的速度分量分别为u、v、w;水平向粘滞系数为vH;垂向粘滞系数为vv;ξ为自由面;g为重力加速度;q为非静水压力。
1.2 边界条件
自由面的压力边界条件为
q|z=ξ=0
(5)
当垂向流速满足式(5)的边界条件时水平流速满足
(6)
在SWASH中关注入流边界位置,其边界条件的设定,需要明确速度参数,同时考虑弱反射问题[22]
(7)
式中:ub为入流边界的流速;ξb为边界入射波的波幅;式(7)中边界位置是通过正负号来描述的,如表现为+号,则入流边界的位置处在南、西,如表现为-号,则位置处在东、北。SWASH中利用干湿处理技术来描述动边界。在模型设置中给定最小水深值,在计算的单位时间步长中对网格点进行干湿判断,当计算的网格点水深低于最小水深时,将该网格点的水深设为最小水深,避免模型计算出现负水深引起的模型运行中断。
1.3 数值求解
模型计算采用有限差分格式进行空间离散,垂向采用σ分层网格,变量通过交错网格方式布置。非静水压力q定义在单元边中心,如图1所示。

图1 网格垂向分层和变量布置示意图

2 SWASH模型验证
2.1 物理模型简介
物理模型布置如图2所示,区域长60 m、宽42 m,模型比尺为1:50。在距造波机34 m处设置坡度为1:8的斜坡模拟礁前斜面,斜面后接长度为14 m的水平平台模拟礁坪,在礁坪中间存在宽度为6 m的裂口,礁坪后存在宽度为5 m的潟湖,最后在潟湖后设置坡度为1:3.3的礁后斜坡。实验中采集波面使用的是47根LG1型电容式浪高仪(G1~G47),由于该礁坪-潟湖-裂口系统物理模型关于裂口对称,所以大部分仪器主要布置在裂口的一侧。

图2 模型布置图(单位:m)
2.2 模型参数设置及验证结果
本文主要研究规则波情况下珊瑚岛礁地形的环流特性,对应的验证工况为:礁坪淹没水深hr=0.04 m,外海入射波高H0=0.04 m,周期T0=2 s。波浪入射为垂直左边界入射,为使模型计算稳定在右边界处设置5 m海绵层。垂向分层为4层,糙率设置曼宁粗糙系数n为0.01。
由图3礁坪上测点的波面历时过程对比可知,在礁缘波浪破碎处的数值模拟结果和物理模型结果吻合较好,说明SWASH模型对于波浪破碎时的波面变化可以较为准确的模拟。裂口和潟湖不同测点的波面历时曲线数值模拟和物理模型趋势基本一致,数据吻合效果较好。

图3 波面数模结果和实测值对比
图4分别对比了礁坪中心线(图4-a)和裂口中心线处(图4-b)在x方向的物理模型和数值模型的向岸平均流速,平均流速取造波稳定后60个周期内的平均。可以看出礁坪上的向岸平均流速数值模拟计算值与实测值吻合较好,在裂口中心线处数值模拟的最大向岸流速比物理模型的偏大,分析原因可能是物理模型是通过摄像机采集的表面浮子的运动轨迹来间接测量表面流场的流速,存在测量误差,而数值模型是计算理想情况下的垂向平均流速,因此输出的表面流速也会随着垂向分层的数量变化有一定的影响,出现了数值模型偏大的结果。
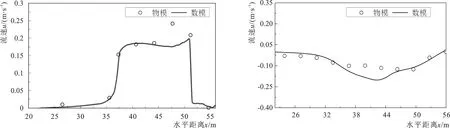
4-a 礁坪中心线 4-b 裂口中心线
3 珊瑚岛礁波生环流模拟
3.1 波浪增水分析

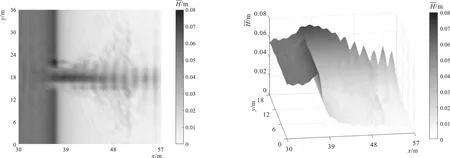
5-a 二维波高云图 5-b三维波面分布图
选取模拟结果中稳定的波面过程求其平均值,得到平均水位(Mean water level, MWL)的空间分布,其相对于静水位为正时则为增水,负值为减水。图6是平均水位沿程变化情况,其中图6-a为二维增水云图,图6-b为三维增水分布图。由图6可知在礁前斜坡上主要以减水为主,波浪在礁缘破碎后出现明显的波浪增水并在靠近礁缘处达到最大,此后逐渐减小。礁坪上的增水向裂口处逐渐减小,这可能是由于在水平方向向裂口回流的影响所致。礁坪上的增水沿岸分布规律为向裂口处逐渐减小。

6-a 二维增水云图 6-b 三维增水分布图
图7为不同外海波要素的礁坪向岸方向中线上沿程平均水位变化趋势图,可以看出礁坪上的沿程平均水位随着波高的增大而增大。波高较大的工况中,在x=36.5 m附近达到最大减水,而入射波高较小的工况较晚达到最大减水(x=37 m),原因是波高较小的工况在礁坪上的波浪破碎强度低于其他工况,且发生位置较晚。波浪破碎后沿程平均水位迅速增大,在x=40 m处达到最大增水,随入射波高增长,最大增水递增倍率在113%~154%。随后沿着礁坪增水持续减小,同时在礁坪上产生向岸方向的压力梯度,驱动向岸方向的波生流。由于波生流的动能在礁后斜坡转化为壅高的势能[9],因此可以看到潟湖位置增水有增大的趋势。礁坪上的沿程平均水位随着周期的增大而增大。但是和改变波高相比,改变周期的平均水位的增长趋势相对不明显。礁坪上的沿程平均水位随着礁坪水深的增大而减小,即在低水位时礁坪的淹没深度要大于高水位,在工程建设中要考虑其影响。
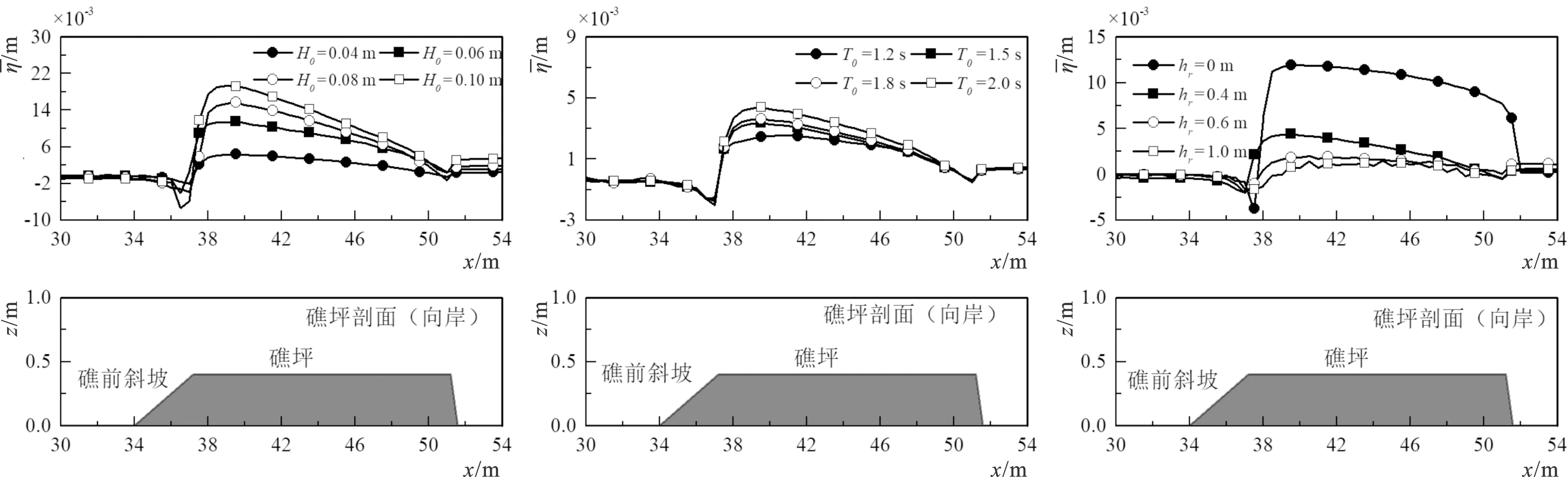
7-a 规则波 T0=2 s,hr=0.04 m 7-b 规则波 H0=0.04 m,hr=0.04 m 7-c 规则波 H0=0.04 m,T0=2 s
3.2 环流流速分析


图8 珊瑚岛礁流场图
由图9可知,礁坪上流向裂口的沿岸流速随着波高增大而增大,礁坪最大向岸流速随着波高的增大而增大,但随入射波高增大流速增长幅度减小。向岸流速和沿岸流速随入射波周期T0的增大而增大,但影响较小。而流速和静水深的关系较为复杂,存在某个静水位(礁坪水深hr=0.04 m)使得流速达到最大值。

9-a 规则波 T0=2 s,hr=0.04 m 9-b 规则波 H0=0.04 m,hr=0.04 m 9-c 规则波 T0=2 s,H0=0.04 m
由图10可知,潟湖处的向岸流速随着波高的增大而增大,其最大值位置较为接近。和礁坪上流速的变化规律类似,潟湖的流速随周期增大而增大,但波高影响较小。沿岸流和静水深的关系较为复杂,在中等水位(礁坪淹没水深hr=0.4 m)流速达到最大值,其原因可能与礁坪上类似,受水深变化引起的增水变化和平均阻力变化的相互作用的影响。

10-a 规则波 T0=2 s,hr=0.04 m 10-b 规则波 H0=0.04 m,hr=0.04 m 10-c 规则波 H0=0.04 m,T0=2 s
由于裂口中不同剖面上的流速差异较大,所以对比离岸流速最大的裂口中线剖面y=18 m处在不同工况中的流速情况。由图11可知,离岸流速随着波高增大而增大,且随着靠近外海的口门,离岸流速增大,离岸流的流出距离增加。中等水位(礁坪淹没水深hr=4 cm)时在裂口整个出流过程中达到最大流速值,与礁坪上流速随水位变化规律相同。但不同水位时的流速变化过程有所差异,中水位时流速最大值出现在裂口偏后位置,其他水位最大值出现在礁缘附近。

11-a 规则波 T0=2 s,hr=0.04 m 11-b 规则波 H0=0.06 m,hr=0.04 m 11-c 规则波 H0=0.04 m,T0=2 s
4 结语
本文采用SWASH模拟了不同的外海波要素和水深对珊瑚岛礁地形的波浪增水和波生环流特性及变化规律进行了分析。主要结论如下:
(1)波浪由深水传播到礁前斜坡发生破碎,波高迅速衰减,礁坪边缘靠近裂口的向岸剖面上沿程最大波高可达其他位置2倍以上。入射波高越大、静水深越小的工况破碎后波高衰减更多,高水位工况波高破碎位置较晚,且破碎前波高增大比例更大。礁前斜坡发生波浪减水后行进约一倍深水波长达到最大增水,裂口的存在使得礁坪上靠近裂口位置的增水减小。礁坪上的波浪增水随外海入射波高、周期的增大而增大,随礁坪的淹没水深增大而减小,与波高、水深相比,周期的影响较小。
(2)在增水正压力和辐射应力的驱动下礁坪上产生向岸流,在礁坪靠近裂口边缘处和潟湖中发生方向旋转,在裂口中形成离岸流通向外海,从而形成外海-礁坪-潟湖-裂口的水平环流系统。在固定裂口和潟湖宽度情况下,不同外海波浪入射要素和礁坪水深的工况的流速分析表明,礁坪、潟湖和裂口中流速随入射波高增大而增大,而周期对礁坪上流速影响较大,即随周期增大流速增大,对于澙湖和裂口中的流速影响较小。在不同礁坪水深中,受辐射应力和底摩阻的相互作用影响,在中等水位时达到最大流速值。
